Complete Solutions to paragraph of chapter RIGID BODIES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODIES AND ROTATIONAL MOTION |
| PHYSICS GALAXY | paragraph |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocity `omega`. Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed ofthe composite disc will be:
View SolutionA rod of mass M and length l is suspended freely from its endandit canoscillate in the vertical plane about the point of suspension. It is pulled to one side and then released. It passes through the equilibrium position withangular speed `omega` . What is the kinetic energy while passing through the mean position ?
View SolutionA tube of length L is filled completely with an incomeressible liquid of mass M and closed at both the ends. The tube is then rotated in a horizontal plane about one of its ends with a uniform angular velocity `omega.` The force exerted by the liquid at the other end is
View SolutionWe have two spheres, one of which is hollow and the other solid. They have identical masses and moment of intertia about their respective diameters. The ratio of their radius is given by.
View SolutionA Stick of length L and mass M lies on a fnctionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shownin figure-5.115. If after the collision ball comes to rest, then what should be the mass of the ball ?

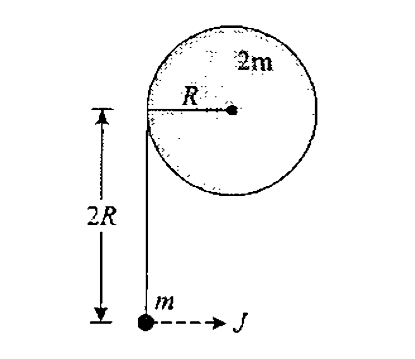
View SolutionA uniform circular disc of mass 2 m and radius R placed freely on a horizontal smooth surface as shown in the figure- 5.116.A particle of mass m is connected to the circumference of the disc with a massless string. Now an impulse J is applied on the particle in the directions shown by dotted line. The acceleration of centre of mass of the disc just after application of implues is `("If J "= 10 N -sec ., m=sqrt10 kg and R= 25cm )`
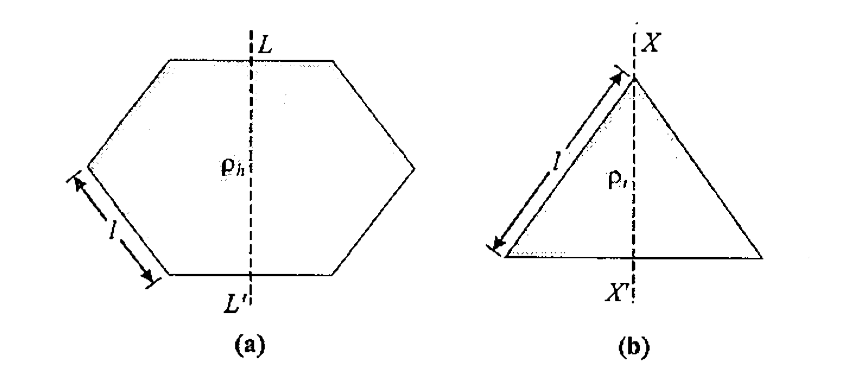
View SolutionMoment of inertia of a uniform hexagonal plate about an axis 'LL' is'I' as shown in the figure-5.117. The moment of inertia (about axisXX') of an equilateral uniform triangular plate of thickness double that of the hexagonal plateis (Ratio of specific gravity `(rhot)/(rhoh)=3`):
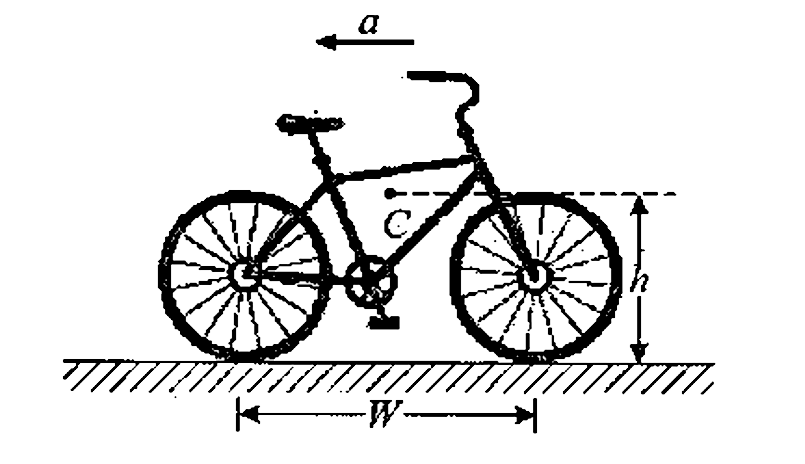
View SolutionA simplified model of a bicycle of mass M has two tires that each comes into contact with the ground at a point. The wheel base of this bicycle is JV, and the centre of mass C of the bicycle is located mid way between the tires and a height h above the ground.The bicycleis moving to the right,but slowing down at a constant acceleration a. Air resistance may be ignored. Assuming that the coefficient of sliding friction between each tyre and the ground is ` mu` and that both tyres are skidding (sliding without rotating). Express your answer in terms of w,h,M and g .
What is the maximum value of `mu` so that both tires remain in contact with the ground :
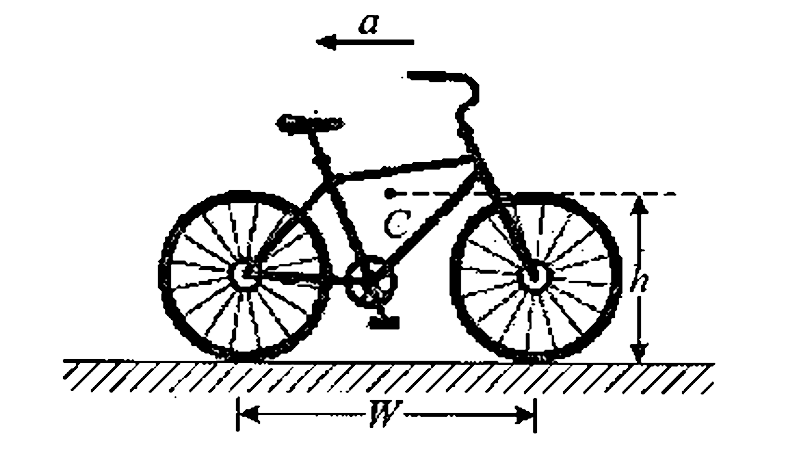
View SolutionA simplified model of a bicycle of mass M has two tires that each comes into contact with the ground at a point. The wheel base of this bicycle is JV, and the centre of mass C of the bicycle is located mid way between the tires and a height h above the ground.The bicycleis moving to the right,but slowing down at a constant acceleration a. Air resistance may be ignored. Assuming that the coefficient of sliding friction between each tyre and the ground is ` mu` and that both tyres are skidding (sliding without rotating). Express your answer in terms of w,h,M and g .
What is the maximum value of a so that both tyres remain in contact with the ground ?
View SolutionA rod of mass m and length 2R can rotate about an axis passing through O invertical plane.A disc of mass m and radius `R//2` is hinged to the other end P ofthe rod and can freely rotate about P. When disc is at lowest point both rod and disc has angular velocity `omega`. If rod rotates by maximum angle`theta=60^(@)` with downward vertical, then `omega` interms of R and g will be(all hinges are smooth)

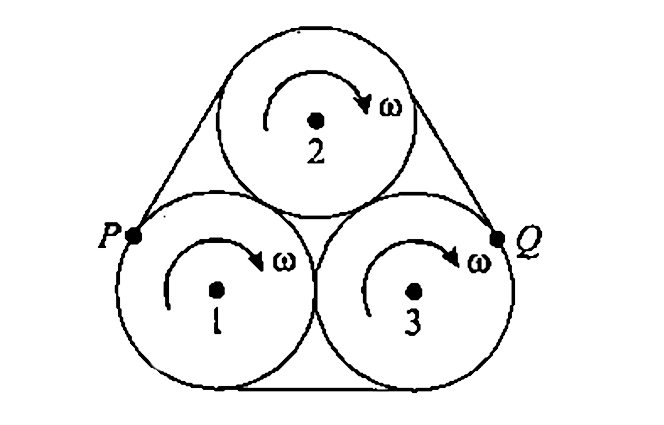
View SolutionThree identical cylinders of radius R are in contact.Each cylinder is rotating with angular velocity `omega`.A thin belt is moving without sliding on the cylinders. Calculate the magnitude of velocity of point P with respect to Q.P and Q are two points of belt which are in contact with the cylinder.
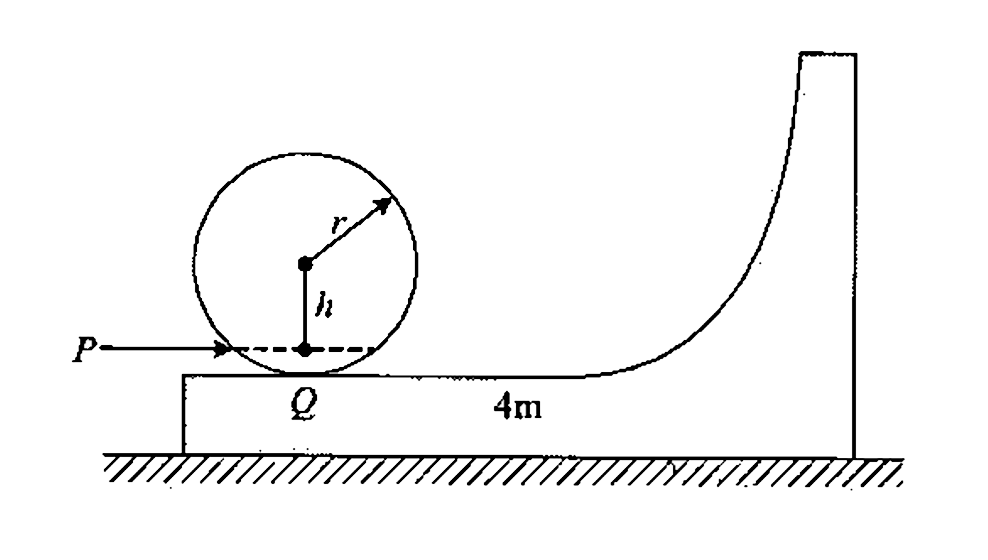
View SolutionIf no external force is acting on the system,net linear momentum of the system is conserved.If system is acted upon by some external force,the component of momentum of the system,along which no external force is present or their vector sum is zero,is conserved. If a sharp blow is given to a body its linear momentum changes immediately.Changein angular momentum not only depends on the magnitude of the blow but also on point ofapplication.In the case of symmetrical body we take the axis of rotation through center of the body. A wedge of mass 4m is placed at rest on a smooth horizontal surface. A uniform solids phere of mass m and radiusr is placed at reston the flat portion of the wedge at the point Q as shown in the figure. A sharp horizontal impulse P is given to the sphere at a point below `h=0.4r`from the center of the sphere.The radius of curvature of the curvedportion of the wedge is R.Coefficient off riction to the left side of point Q is `mu` and to the right side of point Q is zero. For a body to rollon a surface without slipping, there should be no relative velocity between the points of contact.
The maximum height to which the center of mass of the sphere will climb on the curved portion of the wedge is

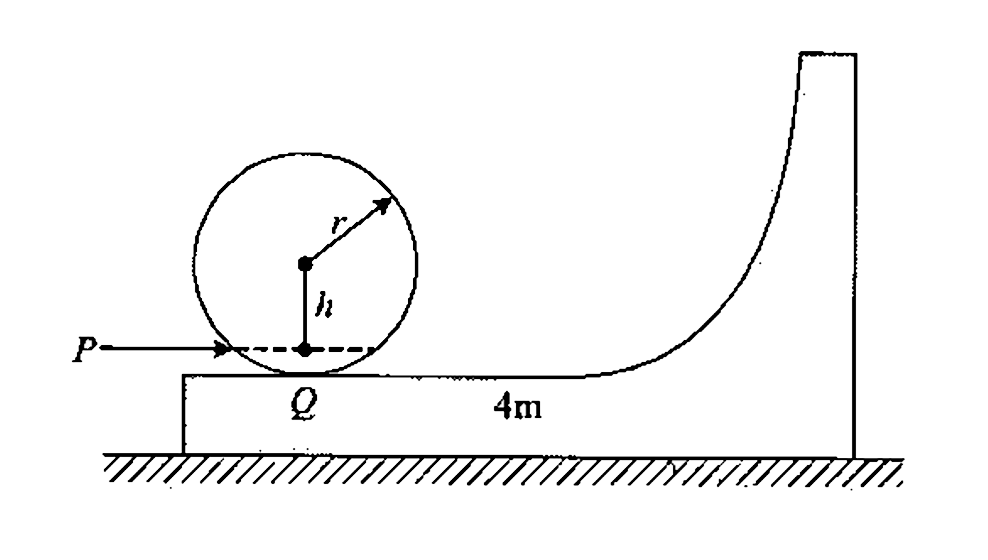
View SolutionIf no external force is acting on the system,net linear momentum of the system is conserved.If system is acted upon by some external force,the component of momentum of the system,along which no external force is present or their vector sum is zero,is conserved. If a sharp blow is given to a body its linear momentum changes immediately.Changein angular momentum not only depends on the magnitude of the blow but also on point ofapplication.In the case of symmetrical body we take the axis of rotation through center of the body. A wedge of mass 4m is placed at rest on a smooth horizontal surface. A uniform solids phere of mass m and radiusr is placed at reston the flat portion of the wedge at the point Q as shown in the figure. A sharp horizontal impulse P is given to the sphere at a point below `h=0.4r`from the center of the sphere.The radius of curvature of the curvedportion of the wedge is R.Coefficient off riction to the left side of point Q is `mu` and to the right side of point Q is zero. For a body to rollon a surface without slipping, there should be no relative velocity between the points of contact.
Kinetic energy ofthesystem when sphere isatthehighest point is :
View SolutionIf no external force is acting on the system,net linear momentum of the system is conserved.If system is acted upon by some external force,the component of momentum of the system,along which no external force is present or their vector sum is zero,is conserved. If a sharp blow is given to a body its linear momentum changes immediately.Changein angular momentum not only depends on the magnitude of the blow but also on point ofapplication.In the case of symmetrical body we take the axis of rotation through center of the body. A wedge of mass 4m is placed at rest on a smooth horizontal surface. A uniform solids phere of mass m and radiusr is placed at reston the flat portion of the wedge at the point Q as shown in the figure. A sharp horizontal impulse P is given to the sphere at a point below `h=0.4r`from the center of the sphere.The radius of curvature of the curvedportion of the wedge is R.Coefficient off riction to the left side of point Q is `mu` and to the right side of point Q is zero. For a body to rollon a surface without slipping, there should be no relative velocity between the points of contact.
Speed ofthe wedge when spherereaches the flat portion again:
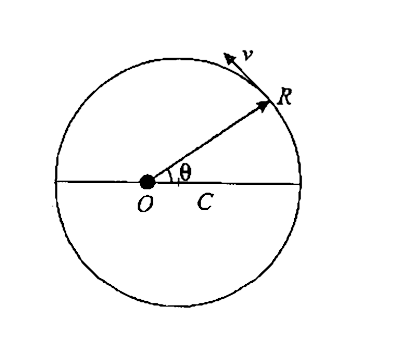
View SolutionA particle is revolving in a circular path as shownin figure in the horizontal plane such that the angular velocity of the particle about the point O is constant and is equal to `1 rad//s`. Distance of the particle from O is given by`R=R_(0)-betat` where `R_(0)`and `Beta` are constant. The speed ofthe particle,as afunction of time is: ltbrlt
View SolutionA particle is projected horizontally with velocity`V_(0)=sqrt(2ga)` along the smooth inside surface of a fixed hollow hemisphere of inner radius 'a' at the level of the centre 'O'. The subsequent motion of the particle is confined between the horizontal planes one through the centre and the other at a depth h. Find the value of h:
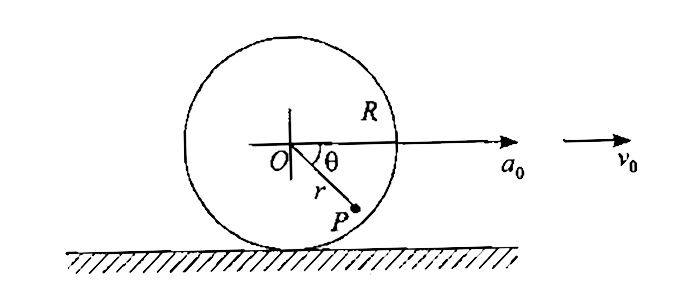
View SolutionThe wheel of radius R rolls with out slipping on horizontal rough surface, and its centre O has an horizontal acceleration in `a_(0)` forward direction. A point P on the wheel is a distancer `r` from O and angular position `theta` from horizontal. For the given values of `a_(0)` R and r, determine the angle `theta` for which point P has no acceleration in this position.
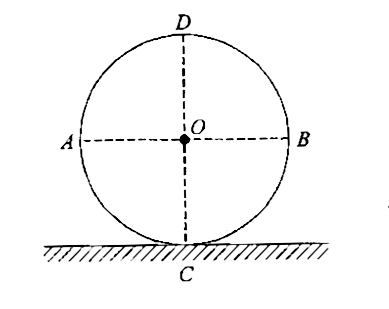
View SolutionA uniform ring of mass m and radius R is in uniform pure rolling motion on a horizontal surface. The velocity of the centre of ring is `V_(0)`. The kinetic energy of the segment ABC is:
View SolutionLer l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle `theta` with AB. The moment of inertia of the plate about the axis CD is then equal to
View SolutionA rectangular block has a square base measuring `axxa` and its height is `h`. It moves on a horizontal surface in a direction perpendicular to one of the edges. The coefficient of friction is `mu`. It will topple if
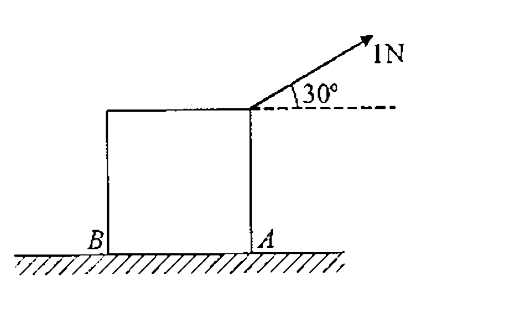
View SolutionA cubical block ofmass `sqrt(3)/(10)` kg and edge 20cm is placed on a rough horizontal surface as shown in the figure-5.126. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the surface on the block acts `(g= 10 m//s^(2))`
View SolutionA rope of mass'm' is looped in a circle of radius R and rotated with a constant angular velocity about its axis in gravity free space . Find the tension in the rope ?
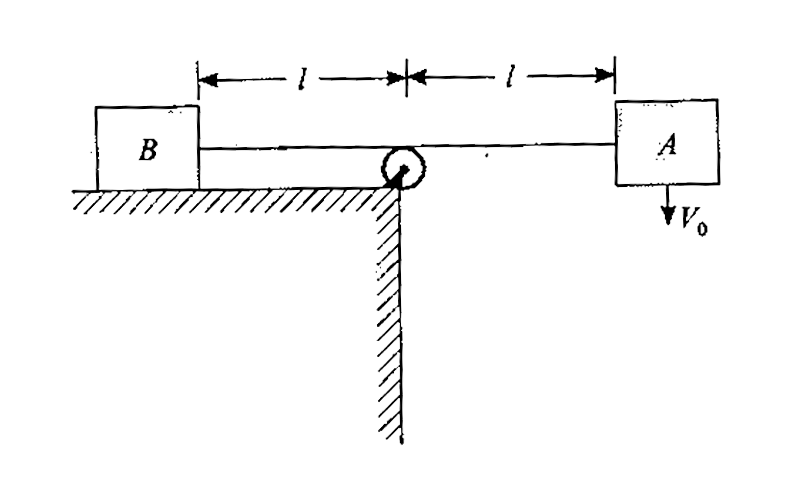
View SolutionTwo identical blocks are placed on as mooth horizontal surface, connected by a light string of length 2I. String touches a fixed smooth pulley at its mid-point initially. Which is attached to two smooth vertical walls as shown in figure-5.127. Blocks is given a speed `V_(0)`perpendicular to string as shown indiagram. B strikes the pulley and stops.
Speed of block B gwhen it hits the pulley is :

View SolutionTwo identical blocks are placed on as mooth horizontal surface, connected by a light string of length 2I. String touches a fixed smooth pulley at its mid-point initially. Which is attached to two smooth vertical walls as shown in figure-5.127. Blocks is given a speed `V_(0)`perpendicular to string as shown indiagram. B strikes the pulley and stops. .
Speed of A when it hits the wall is :
View Solution
paragraph questions and complete solutions for chapter RIGID BODIES AND ROTATIONAL MOTION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11