Complete Solutions to Illustration of chapter RIGID BODIES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | RIGID BODIES AND ROTATIONAL MOTION |
| PHYSICS GALAXY | Illustration |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Find the moment of inertia about `A A'` of a spherical ball of mass `m` and radius `r` attached at the end of a straight rod of mass `M` and length `l`, if this system is free to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).

View SolutionA rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as `rho = ax^(2) + b` kg/m
View SolutionFind moment of inertia of half disc of radius `R_2` and mass `M` about its centre. A smaller half disc of radius `R_1` is cut from this disc

View SolutionFind the acceleration of `m_(1)` and `m_(2)` in an Atwood's Machine if there is friction present between surface of pulley and the thread and thread does not slip over the surface ofpulley. Moment of inertia of pulley is I.
View SolutionA uniform disc of radius R and mass M is mounted on an axis supported in fixed friction less bearing. A light cord is wrapped around the rim of the wheel and suppose we hang a body of mass m from the cord.
(a) Find the angular acceleration of the disc and tangential acceleration ofpoint on the rim.
(b) At a moment t= 0, the system is set in motion, find the time dependence of the angular velocity of the system and the kinetic energy ofthe whole system.
View SolutionA uniform cylinder of radius `r` and mass `m` can rotate freely about a fixed horizontal axis. A thin cord of length l and mass `m_(0)` is would on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length `x` of the hanging part of the end. the wound part of the cord is supposed to have its centre of gravity on the cylinder axis is shown in figure.

View SolutionA cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate
(a) The downward linear acceleration of the cylinder
(b) The tension in the strings
(c) The time dependence of the instantaneous power developed by gravity
View SolutionThe arrangement shown in figure consists of two identical, uniform, solid cylinders, each of mass `m`, on which two light theads are wound symmetrically.
Find the tensions of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.

View SolutionIn an At wood's machine the pulley mounted in horizontal frictionless bearings has a radius R=0.05m.The cord passing over the pulley carries a block of mass `m_(1) =0.75` kg at one end and a block of mass`m_(2) = 0.50` kg on the other end . When set free from rest, the heavier block is observed to fall' a distance 1 metre in 10 seconds. Find the moment ofinertia of the pulley.
View SolutionFind total energy of the inclined rod of mass m shown in figure-5.39 , rotating with angular velocity `omega` , about a vertical axis XX', shown in figure .

View SolutionFind the angular momentum of the system of at wood's machine used in example-5.4 after t second from start about point O, the axle ofpulley.
View SolutionConsider a cylinder rolling on a horizontal plane. Its linear velocity is `v` and rotational angular velocity is `omega`. Find its angular momentum about point `P` on the ground as shown in Fig. What happens to this angular momentum if the cylinder is rotating in opposite direction but moving translationally in the same direction.

View SolutionA disc with moment of inertia`I_(1)`, is rotating with an angular velocity `omega_(1)` about a fixed axis. Another coaxial disc with moment of inertia `I_(2)`, which is at rest is gently placed on the first disc along the axis. Due to friction discs slips against each other and after some time both disc start rotating with a common angular velocity. Find this common angular velocity.
View SolutionA child of mass `m` is standing, on the periphery of a circular platform of radius `R`, which can rotate about its central axis. The moment of inertia of the platform is `I`. Child jumps off from the platform with a velocity `u` tangentially relative to the platform. Find the angular speed of the platform after the child jumps off.
View SolutionSuppose in the previous poroblem, the child stays at rest on the platform and one of hils firend throws a ball of mas `m_(1)` towards thim with a velocity of `v` from a direction tangential to the platform and the child on the platform catches the ball. Find the angular velocity of the platform after he catches the ball.
View SolutionIn previous problem, if initially the platform with the child is rotating with an angular speed `omega_(1)`. If child start walking along its periphery in opposite direction with speed u relative to platform, what will be the new angular speed ofthe platform.
View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed `omega`. It picks up a stationary particle of mass `m` at its edge. Find the new angular speed of the wheel.
View SolutionA turn table of mass M and radius R is rotating with angular velocity `omega_(0)` on frictionless bearing. A spider of mass m falls vertically onto the rim of the turn table and then walks in slowly towards the centre ofthe table. What is the angular velocity of the system when spider is at a distance r from the centre. Compute also the angular velocity of the turn table when the spider is at the rim and at the centre of the table .Is the energy of the system in this problem conserved ?
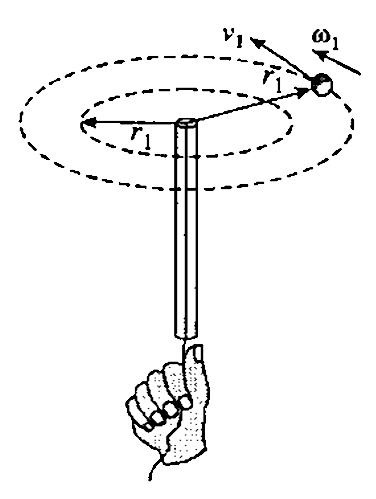
View SolutionA point mass is tied to one end of a cord whose other end passes through a vertical hollow tube , caught in one hand. The point mass is being rotated in a horizontal circle ofradius 2 m with speed of 4m/sec.The cord is then pulled down so that the radius of the circle reduces to 1m . Compute the new linear and angular velocities of the point mass and compute the kinetic energies under the initial and final states.
View SolutionTwo cylinders having radiii `R_(1)` and `R_(2)` and rotational inertia `I_(1)` and `I_(2)` respectively, are supported by fixed axes perpendicular to the plane of figure-5.52. The large cylinder is initially rotating with angular velocity`omega_(0)`. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually, slipping ceases, and the two cylinders rotate at constant rates in opposite directions, (a) Find the final angular velocity `omega_(2)` of the small cylinder in terms of `I_(1) , I_(2) , R_(1) , R_(2)` and `omega_(0)`. (b) Is total angular momentum conserved in this case ?
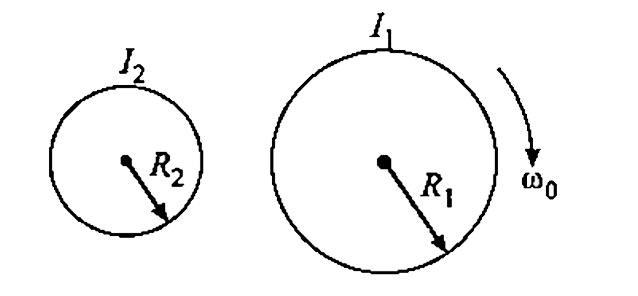
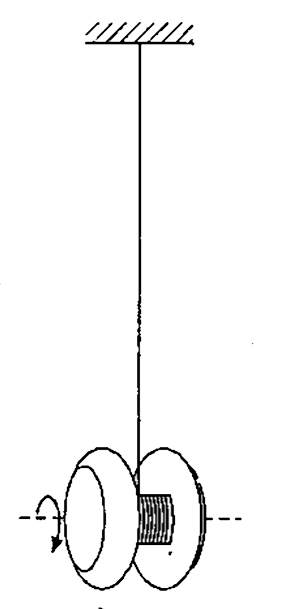
View SolutionA primitive yo-yo is made by wrapping a string several times around a solid cylinder with mass M and radius R shown in figure-5.56. The end of the string stationary while releasing the cylinder with no initial motion. The string unwinds but does not slip or Stretch as the cylinder drops and rotates. Use energy considerations to find the speedv ofthe centre ofmass ofthe solid cylinder after it has dropped a distance h.
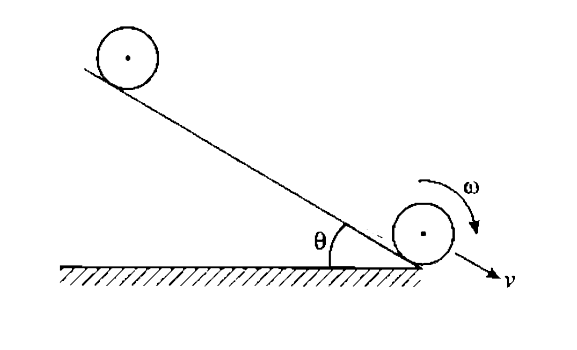
View SolutionA rolling body (it.can be ring, sphere,... etc) rolls down from the top of an inclined plane as shown in figure-5.57. Find how its velocity depends on its geometry.
View SolutionA force `F` acts tangentially at the highest point of a sphere `f` mass m kept on a rough horizontal plane. If the sphere rolls without slipping, find the acceleration of the centre of the sphere.

View SolutionA cylinder of radius `R` and mass `M` rolls without slipping down a plane inclined at an angle `theta`. Coeff. of friction between the cylinder and the plane is `mu`. For what maximum inclination `theta`, the cylinder rolls without slipping ?
View SolutionA plank of mass M is placed on a smooth surface over which a cylinder of mass m and radius R is placed as shown in figure-5.63. Now the plank is pulled towards right with an external force F. If cylinder does not slip over the surface of plank find the linear acceleration of plank and cylinder and the angular acceleration of the cylinder.
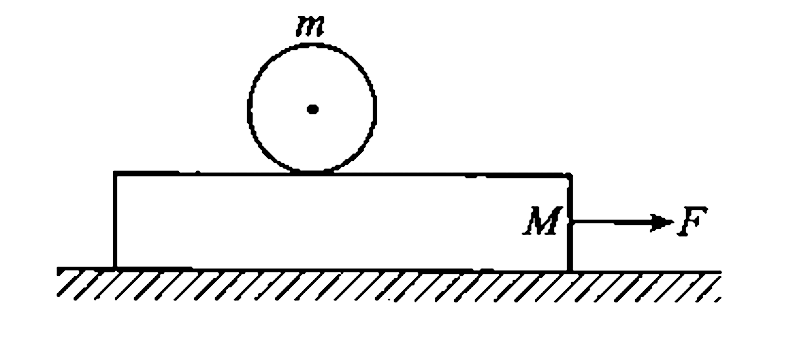
View Solution
Find the acceleration of the cylinder of mass `m` and radius `R` and that of plank of mass `M` placed on smooth surface if pulled with a force `F` as shown in figure. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.
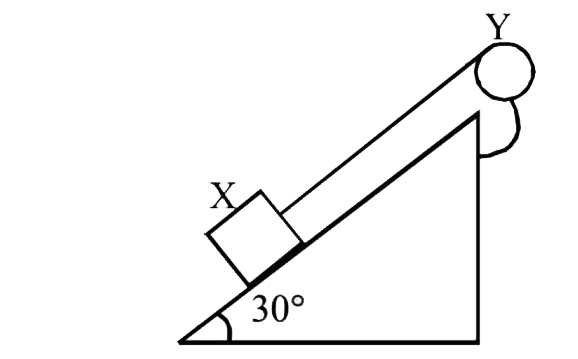
View SolutionA block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination `30^@` to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2 and of radius 0.2 m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s `10 rad s^(-1)` calculate the distance travelled by X from that instant of time until it comes to rest
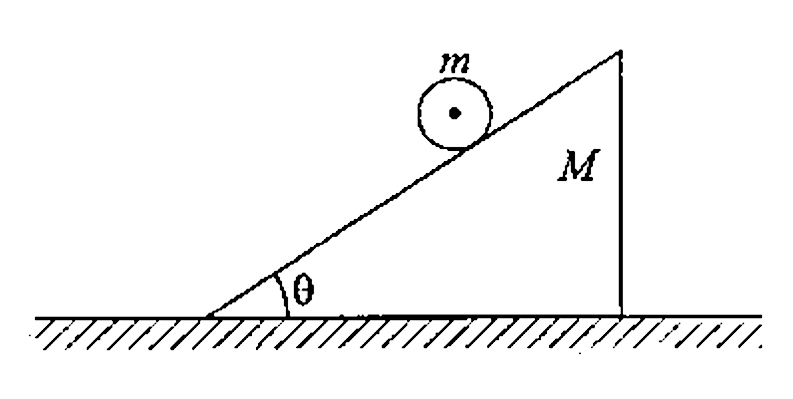
View SolutionA rough wedge of mass M is free to move on a smooth horizontal plane as shown in figure-5.69.The uniform cylinder of mass m is placed on the wedge and it begins to roll down without slipping . Show that the acceleration of cylinder on the surface of wedge is given as
`a = (2g "sin"theta(m + M))/(m + 3M + 2msin^(2)theta)`
View SolutionA thin spherical shell of radius `R` lying on a rough horizontal surface is hit sharply and horizontally by a cue. Where should it be hit so that the shell does not slip on the surface?
View SolutionA uniform solid cylinder of mass `m` and radius `R` is set in rotation about its axis with an angular velocity `omega_(0)`, then lowered with its lateral surface onto a horizontal plane and released. The coefficient of friction between the cylinder and the plane is equal to `mu`. Find
(`a`) how long the cylinder will move with sliding,
(`b`) the total work performed by the sliding friction force acting on the cylinder.
View SolutionA billiard ball is struck by a cue. The line of action of the applied impulse is horizontal andpasses through thecentre of theball. The initial velocityofthe ball is `v_(0)`. If is the radius, M is the mass of the ball and `mu` is the coefficient of friction between the ball and the floor, find how far the ball moves before it ceases to slip on the floor.
View SolutionA small disc and a thin uniform rod of length l, whose mass is `eta` times greater than the mass of the disc, lie on a smooth horizontal plane. The disc is set in motion, in horizontal direction and perpendicular to the rod, with velocity v, after which it elastically collides with the end of the rod. Find the velocity of the disc and the angular velocity of the rod after the collision. At what value of `eta` will the velocity of the disc after the collision be equal to zero? reverse its direction?
View Solution
Illustration questions and complete solutions for chapter RIGID BODIES AND ROTATIONAL MOTION of GK PUBLICATIONS PHYSICS (HINGLISH) of Class 11