Complete Solutions to Exercise- 2 PART - III of chapter ELASTICITY AND VISCOCITY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | ELASTICITY AND VISCOCITY |
| RESONANCE | Exercise- 2 PART - III |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
The wires `A` and `B` shown in Fig. are made of the same material and have radii `r_(A)` and `r_(B)`, respectively. The block between them has a mass `m`. When the force `F` is `mg//3`, one of the wires breaks. Then

View SolutionWhen a tensile or compressive load `'P'` is applied to rod or cable, its length changes. The change length `x` which, for an elastic material is proportional to the force Hook' law).
`P alpha x` or `P = kx`
The above equation is similar to the equation of spring. For a rod of length `L`, area `A` and young modulue `Y`. the extension `x`can be expressed as.
`x = (PL)/(AY)` or `P = (AY)/(x)`, hence `K = (AY)/(L)`
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to `(1)/(2)Px`. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
If rod of length `4m`, area `4cm^(2)` amd young modules `2 xx 10^(10)N//m^(2)` is attached with mass `200 kg`, then angular frequency of SHM `("rad"//"sec.")` of mass is equal to -
View SolutionWhen a tensile or compressive load `'P'` is applied to rod or cable, its length changes. The change length `x` which, for an elastic material is proportional to the force Hook' law).
`P alpha x` or `P = kx`
The above equation is similar to the equation of spring. For a rod of length `L`, area `A` and young modulue `Y`. the extension `x`can be expressed as.
`x = (PL)/(AY)` or `P = (AY)/(x)`, hence `K = (AY)/(L)`
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called strain energy & equal to `(1)/(2)Px`. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by energy conservation.
In above problem if mass of `10 kg` falls on the massless collar attached to rod from the height of `99cm` then maximum extension in the rod is equal (rod of length 4m, area `4cm^(2)` and young modules `2 xx 10^(10)N//m^(2)` `g = 10m//sec^(2)`)-
View SolutionWhen a tensile or compressive load `'P'` is applied to rod or cable, its length changes. The change length `x` which, for an elastic material is proportional to the force Hook' law).
`P alpha x` or `P = kx`
The above equation is similar to the equation of spring. For a rod of length `L`, area `A` and young modulue `Y`. the extension `x`can be expressed as.
`x = (PL)/(AY)` or `P = (AY)/(x)`, hence `K = (AY)/(L)`
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to `(1)/(2)Px`. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
It two rods of same length `(4m)` and cross section areas `2 cm^(2)` and `4 cm^(2)` with same young modulus `2 xx 10^(10)N//m^(2)` are attached one after the other with mass `600 kg` then angular frequency is-
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.

In the given figure as the the plate moves the fluid particle at the surface moves from position `1` to `2` and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
`(F)/(A) alpha (d' theta)/(dt)` but `y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y)`
then `F = eta A(u)/(y), eta =` coefficient of viscosity
for non-linear velocity distribution -
`F = eta A(du)/(dy)`
where `(u)/(y)` or `(du)/(dy)` is known as velocity gradiant.
In the given figure if force of `2N` required to maintain constant velocity of plate, the value of constant `C_(1), & C_(2)` are -

View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
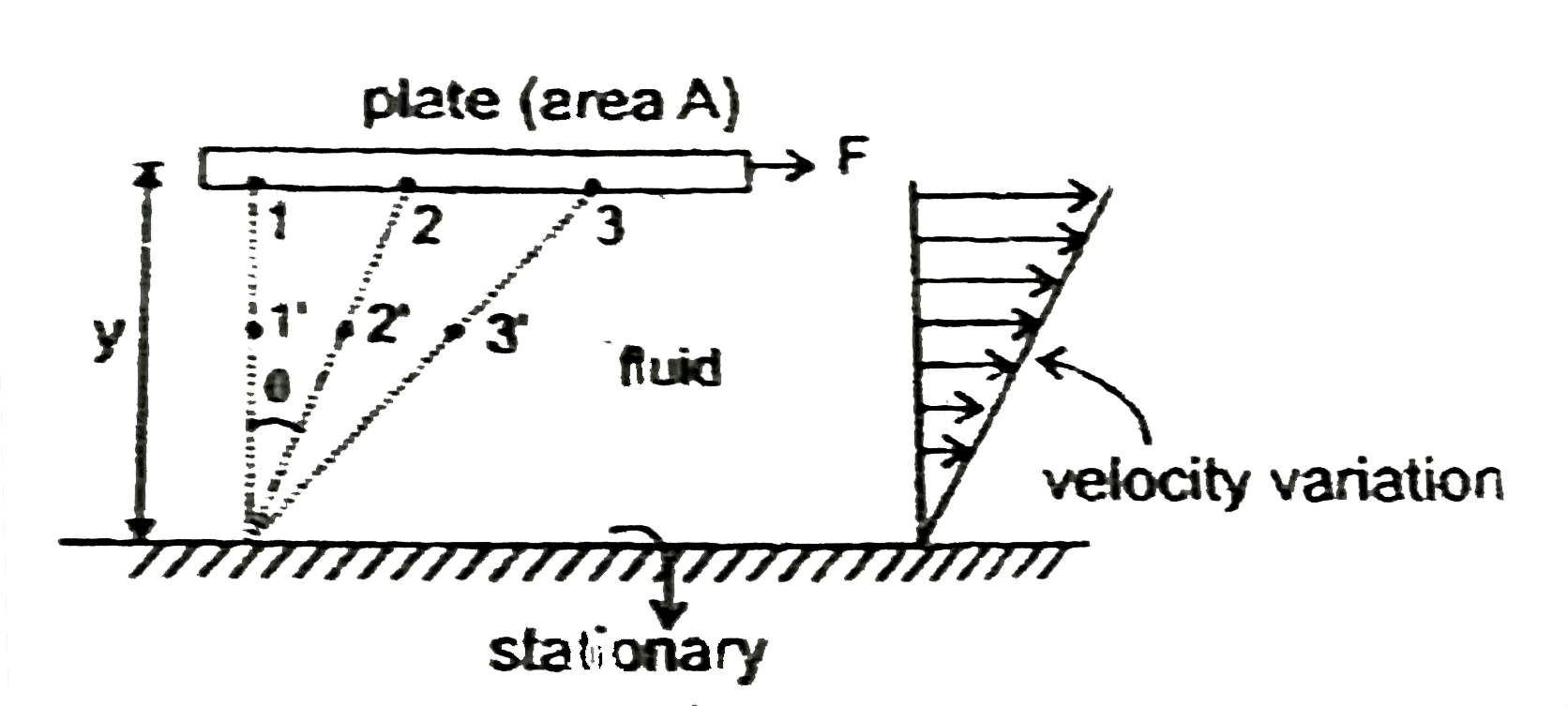
In the given figure as the the plate moves the fluid particle at the surface moves from position `1` to `2` and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
`(F)/(A) alpha (d' theta)/(dt)` but `y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y)`
then `F = eta A(u)/(y), eta =` coefficient of viscosity
for non-linear velocity distribution -
`F = eta A(du)/(dy)`
where `(u)/(y)` or `(du)/(dy)` is known as velocity gradiant.
If velocity distribution is given as (parabolic)
`u = c_(1)y^(2) + c_(2)y + c_(3)`
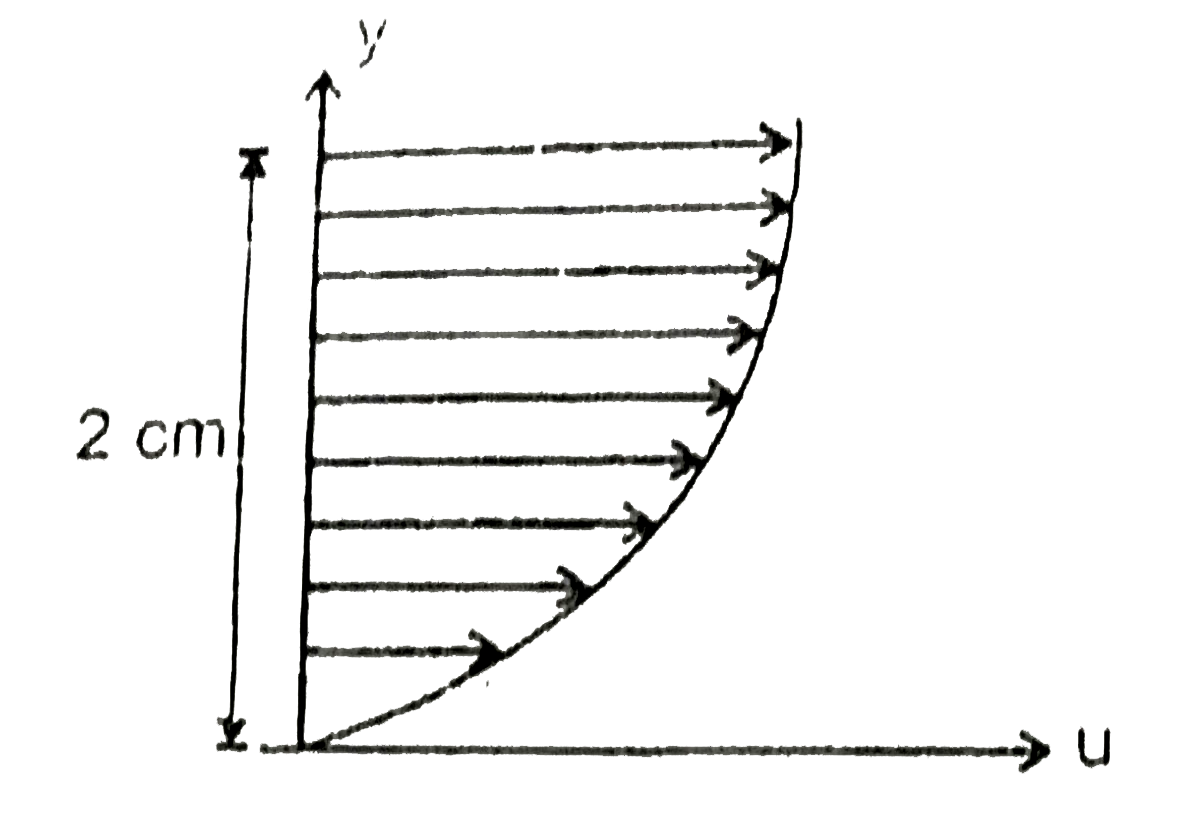 For the same force of `2N` and the speed of the plate `2 m//sec`, and area of plate is 1 and viscousity is .001, the constant `C_(1), C_(2)` & `C_(3)` are
For the same force of `2N` and the speed of the plate `2 m//sec`, and area of plate is 1 and viscousity is .001, the constant `C_(1), C_(2)` & `C_(3)` are
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
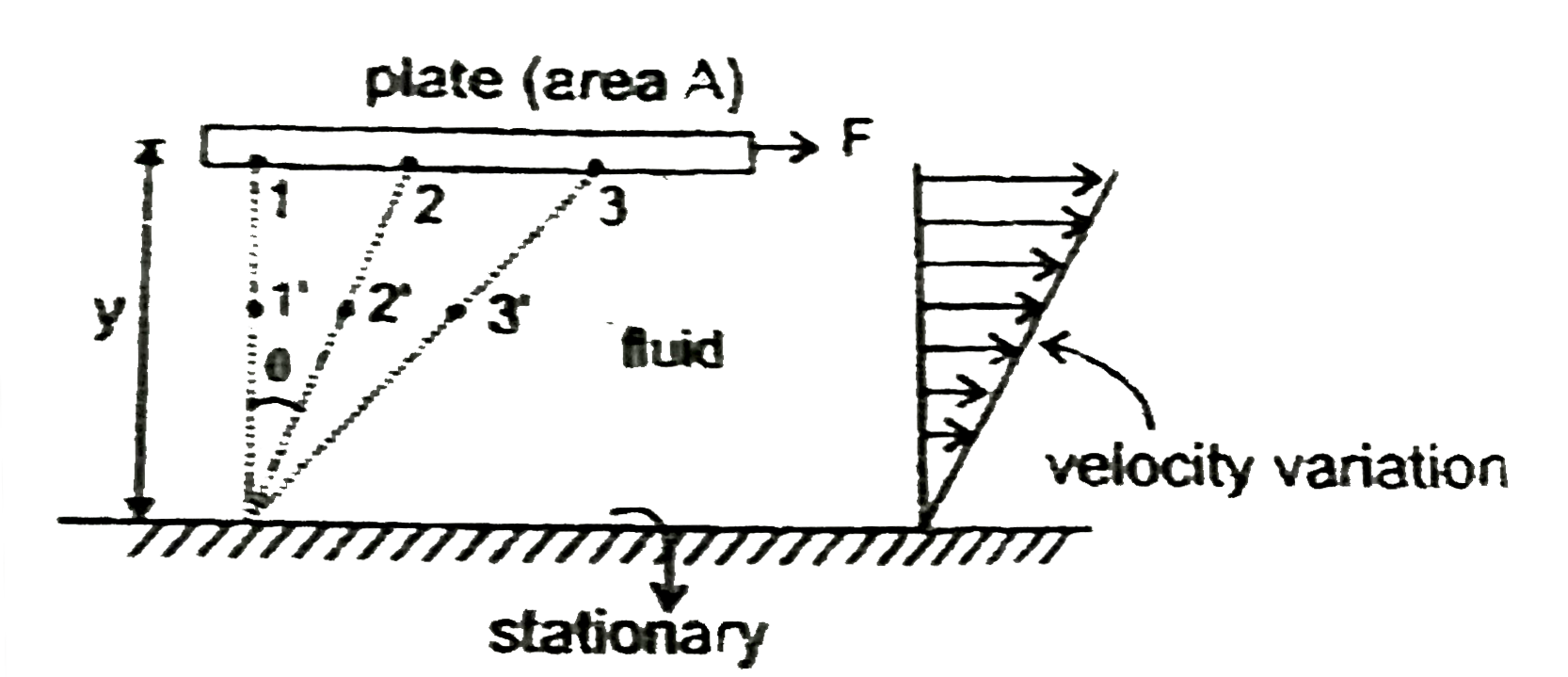
In the given figure as the the plate moves the fluid particle at the surface moves from position `1` to `2` and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
`(F)/(A) alpha (d' theta)/(dt)` but `y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y)`
then `F = eta A(u)/(y), eta =` coefficient of viscosity
for non-linear velocity distribution -
`F = eta A(du)/(dy)`
where `(u)/(y)` or `(du)/(dy)` is known as velocity gradiant.
The velocity gradient just below the plate, in above problem is equal to - (per second)
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
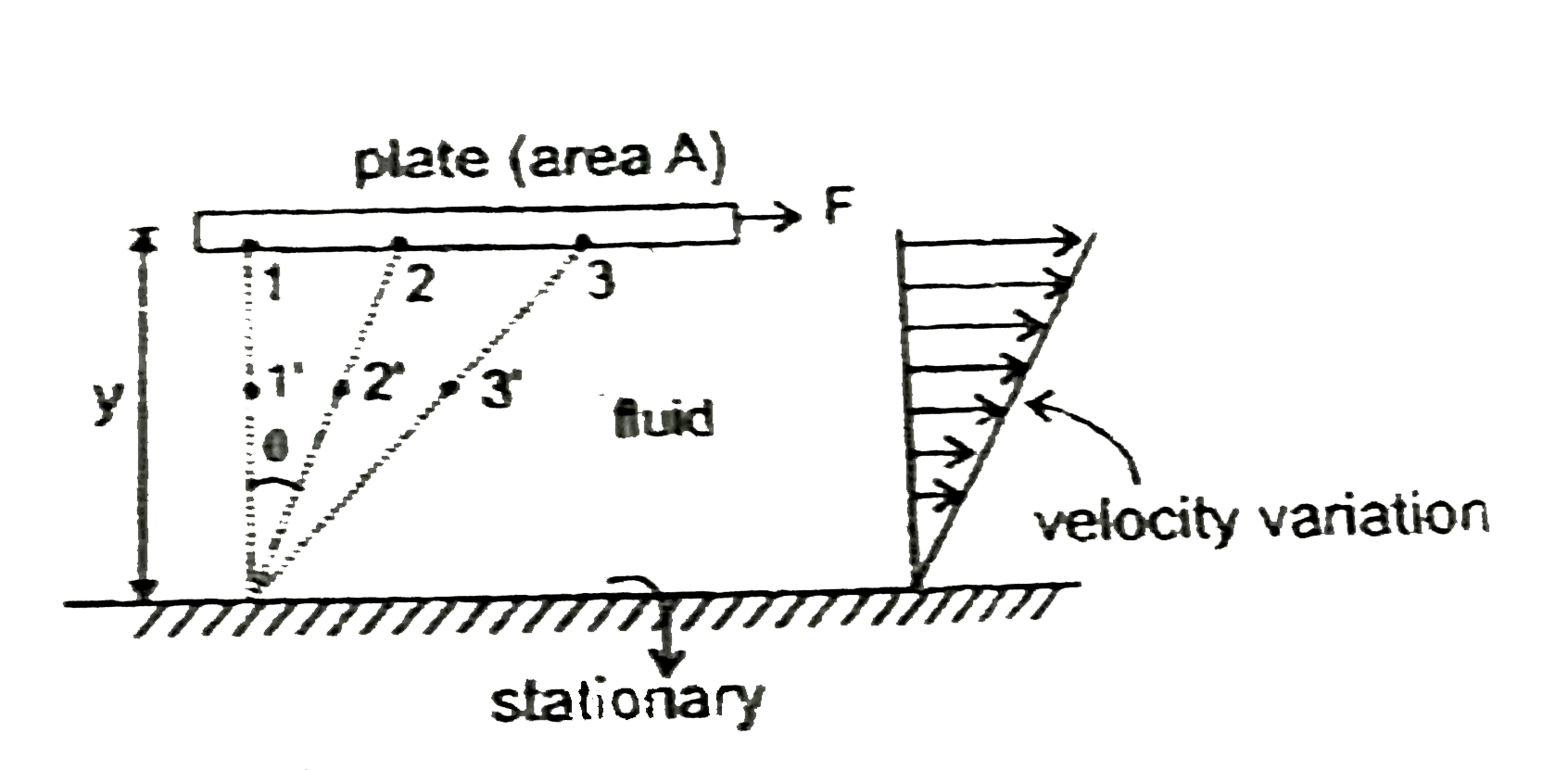
In the given figure as the the plate moves the fluid particle at the surface moves from position `1` to `2` and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
`(F)/(A) alpha (d' theta)/(dt)` but `y = (d' theta)/(dt) = u, (d' theta)/(dt) = (u)/(y)`
then `F = eta A(u)/(y), eta =` coefficient of viscosity
for non-linear velocity distribution -
`F = eta A(du)/(dy)`
where `(u)/(y)` or `(du)/(dy)` is known as velocity gradiant.
The velocity gradient just near the bottom boundary is equal to -
View Solution
Exercise- 2 PART - III questions and complete solutions for chapter ELASTICITY AND VISCOCITY of RESONANCE ENGLISH of Class 11