Complete Solutions to Example of chapter HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HEAT TRANSFER |
| RESONANCE | Example |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
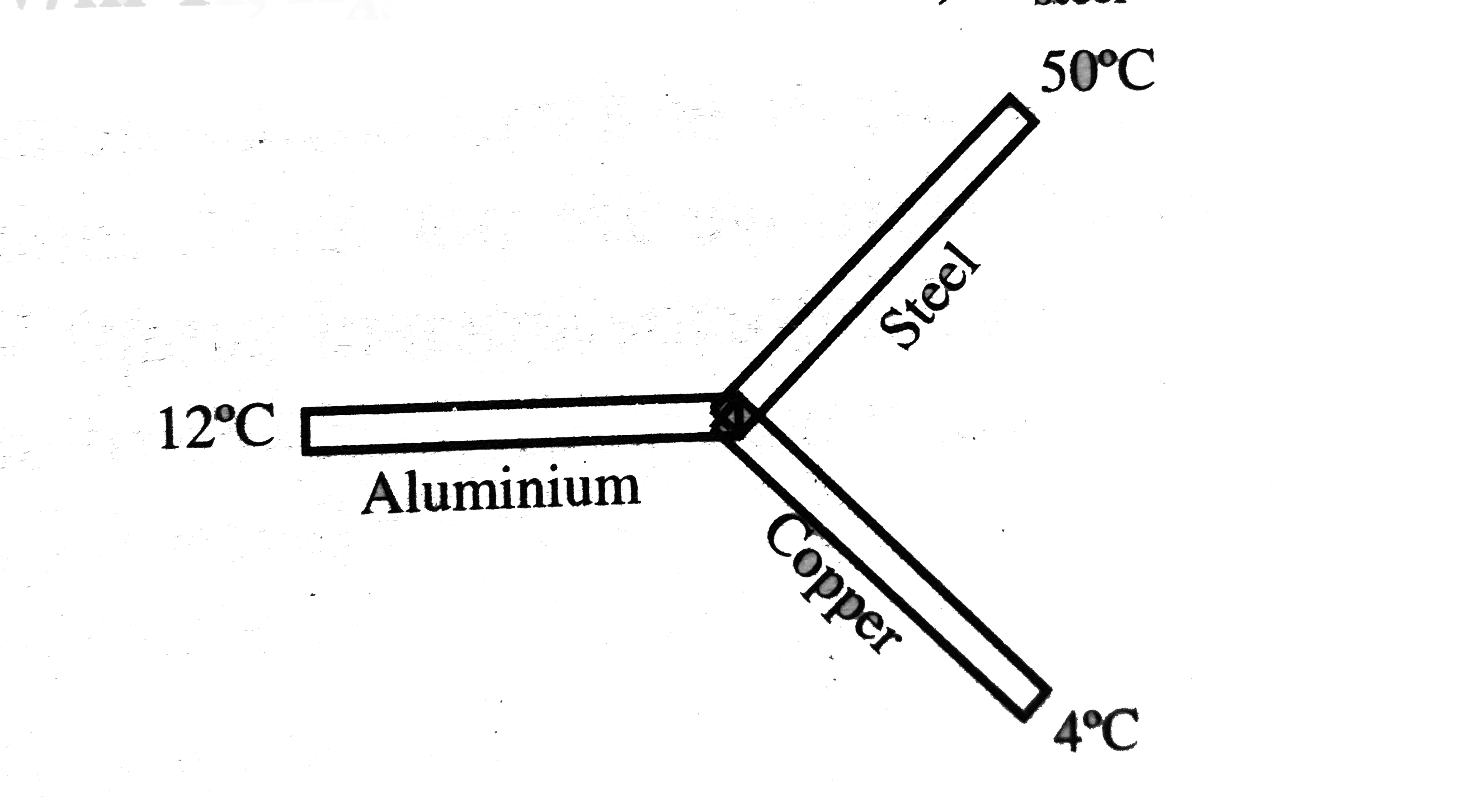
Three identical rods of length 1 m each, having cross-sectional area of `1cm^2` each and made of aluminium, copper and steel, respectively, are maintained at temperatures of `12^@C`,`4^@C` and `50^@C`, respectively, at their separate ends. Find the teperature of their common junction.
`[K_(Cu)=400 W//m-K,K_(Al)=200 W//m-K,K_("steel")=50 W//m-K]`
View SolutionThe figure shows the cross-section of the outer wall of a house buit in a hill-resort to keep the house insulated from the freezing temperature of outside. The wall consists of teak wood of thickness `L_(1)` and brick of thickness `(L_(2) = 5L_(1))`, sandwitching two layers of an unknown material with identical thermal conductivites and thickness. The thermal conductivity of teak wood is `K_(1)` and that of brick is `(K_(2) = 5K_(1))`. Heat conducion through the wall has reached a steady state with the temperature of three surfaces being known. `(T_(1) = 25^(@)C, T_(2) = 20^(@)C` and `T_(5) = - 20^(@)C)`. Find the interface temperature `T_(4)` and `T_(3)`.

View SolutionIn example `3, K_(1) = 0.125 W//m-.^(@)C, K_(2) = 5K_(1) = 0.625 W//m-.^(@)C` and thermal conductivity of the unknown material is `K = 0.25 W//m^(@)C L_(1) = 4cm, L_(2) = 5L_(1) = 20cm`. If the house consists of a single room of total wall area of `100 m^(2)`. then find the power of the electric heater being used in the room.
View SolutionThree copper rods and three steel rods each of length `l = 10 cm` and area of cross-section `1cm^(2)` are connected as shown

If ends `A` and `E` are maintained at temperatures `125^(@)C` and `0^(@)C` respectively, calculate the amount of heat flowing per second from the hot of cold function. `[K_(Cu) = 400 W//m-K, K_(steel) = 50 W//m-K]`
View SolutionTwo thin conectric shells made of copper with radius `r_(1)` and `r_(2) (r_(2) gt r_(1))` have a material of thermal conductivity `K` filled between them. The inner and outer spheres are maintained at temperature `T_(H)` and `T_(C)` respectively by keeping a heater of power `P` at the centre of the two sphers. Find the value of `P`.
View SolutionA container of negligible heat capacity contains `1kg` of water. It is connected by a steel rod of length `10m` and area of cross-section `10cm^(2)` to a large steam chamber which is maintained at `100^(@)C`. If initial temperature of water is `0^(@)C`, find the time after which it beomes `50^(@)C`. (Neglect heat capacity of steel rod and assume no loss of heat to surroundings) (use table `3.1`, take specific heat of water `=4180 J//kg.^(@)C)`
View SolutionThe solar radiation spectrum reveals that the intensity corresponding to a wavelength of `4750Å` is maximum Estimate the surface temperature of the sun.
(given wien's cosntant`=2.89xx10^-3m-K`)
View SolutionA body of emissivity `(e = 0.75)`, surface area of `300cm^(2)` and temperature `227^(@)C` is kept in a room at temperature `27^(@)C`. Calculate the initial value of net power emitted by the body.
View SolutionA hot black body emits the enegy at the rate of 16 `Jm^-2s^-1` and its most intense radiation corresponds to 20000`Å`. When the temprerature of this body is further increased and its most intense radiation corresponds to `10000Å`, then find the value of energy radiated in `Jm^-2s^-1`.
View SolutionA body at temperature `40^(@)C` is kept in a surrounding of constant temperature `20^(@)C`. It is observed that its temperature falls to `35^(@)C` in `10` minutes. Find how much more time will it taken for the body to attain a temperature of `30^(@)C`.
View Solution
Example questions and complete solutions for chapter HEAT TRANSFER of RESONANCE ENGLISH of Class 11