Complete Solutions to Exercise of chapter HEAT TRANSFER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | HEAT TRANSFER |
| RESONANCE | Exercise |
| Number Of Questions | 91 |
| Academic Year | 2023-24 |
One end of a steel rod `(K=46Js^(-1)m^(-1)C^(-1))` of length `1.0m` is kept in ice at `0^(@)C` and the other end is kept in boiling water at `100^(@)C` . The area of cross section of the rod is `0.04cm^(2)` . Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice `=3.36xx10^(5)Jkg^(-1)` .
View SolutionA rod CD of thermal resistance `5.0 K//W` is joined at the middle of an identical rod AB as shown in figure. The ends A, B and D are maintained at `100^@C` and `25^@C` respectively. Find the heat current in CD.
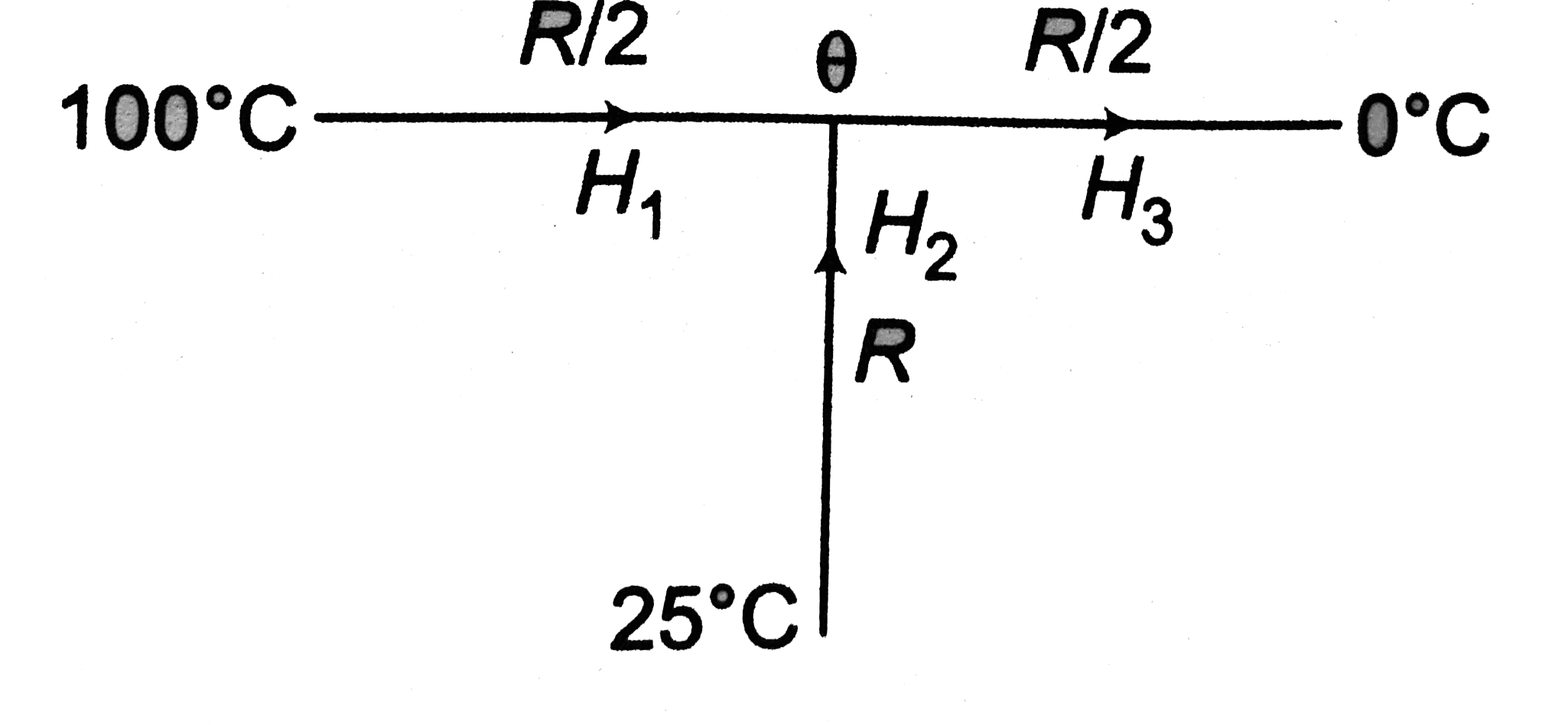
View SolutionA semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the straight rod in a given time.
View SolutionThree slabs of same surface area but different conductivities `k_(1),k_(2),k_(3)` and different thickness `t_(1),t_(2),t_(3)` are placed in close contact. After steady state this combination behaves as a single slab. Find its effective thermal conductivity.

View SolutionA hollow metallic sphere of radius `20cm` surrounds a concentric metallic sphere of radius `5cm`. The space between the two sphere is filled with a nonmetallic material. The inner and outer sphere are maintained at `50^(@)C` and `10^(@)C` respectively and it is found that `100J` of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the sphere.
View SolutionA hollow tube has a length l, inner radius `R_(1)` and outer radius `R_(2)` . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature `T_(1)` and `T_(2)``(T_(2)gtT_(1))` (b) the inside of the tube is maintained at temperature `T_(1)` and the outside is maintained at `T_(2)` .
View SolutionA metal rod of cross sectional area `1.0cm^(2)` is being heated at one end. At one time , the temperature gradient is `5.0^(@)C cm^(-1)` at cross section A and is `2.5^(@)Ccm^(-1)` at cross section B. Calculate the rate at which the temperature is increasing in the part AB `=0.40J^(@)C^(-1)` , thermal conductivity of the material of the rod. `=200Wm^(-1)`^(@)C^(-1)` . Neglect any loss of heat to the atmosphere.
View SolutionWhen `q_(1)` joules of radiation is incident on a body if reflects and transmits total of `q_(2)` joules. Find the emissivity of the body.
View SolutionA blackbody of surface area `1cm^(2)` is placed inside an enclosure. The enclosure has a constant temperature `27(@)C` and the blackbody is maintained at `327^(@)C` by heating it electrically. What electric power is needed to maintain the temperature? `sigma=6.0xx10^(-8)Wm^(-2)K^(-2)` .
View SolutionEstimate the temperature at which a body may appear blue or red. The values of `lambda_(mean)` for these are `5000` and `7500Å` respectively. [Given Wein's constant `b = 0.3 cmK]`
View SolutionThe temperature of a hot liquid in a container of negligible heat capacity falls at the rate of `3K//min` due to heat emission to the surroundings, just before it begins to solidify. The temperature then remains constant for `30min`, by the time the liquid has all solidfied. Find the ratio of specific heat capacity of liquid to specific latent heat of fusion.
View SolutionThe earth receives its surface radiation from the sun at the rate of 1400 `W//m^(2)`. The distance of the centre of the sun from the surface of the earth is `1.5 xx 10^(11)` m and the radius of the sun is `7.0 xx 10^(8)` m. Treating sun as a black body, it follows from the above data that its surface temeperature is
View SolutionA solid copper sphere (density `rho` and specific heat c) of radius r at an initial temperature 200 K is suspended inside a chamber whose walls are at almost 0 K. The time required for the temperature of the sphere to drop to 100 K is _________ `rhonc`
View SolutionA liquid cools from `70^(@)C` to `60^(@)C` in `5` minutes. Calculate the time taken by the liquid to cool from `60^(@)C` to `50^(@)C` , If the temperature of the surrounding is constant at `30^(@)C` .
View SolutionA wall has two layers A and B, each made od=f different material. Both the layers have the same thickness. The thermal conductivity for A is twice that B and, under steady condition, the temperature difference across the wall is `36^(@)`C. The temperature difference across the layer A is
View SolutionTwo metal cubes with 3 cm edges of copper and aluminium are arranged as shown in figure. Find
(i) the total thermal current from one reservoir to the other.
(ii) the ratio of the thermal current carried by the copper cube to that carried by the aluminium cube . thermal conductivity of copper is `401 Wm^(-1) K` and that of aluminium is `237 Wm(-1) K`.

View SolutionTwo metal cubes with 3 cm edges of copper and aluminium are arranged as shown in figure. Find
(i) the total thermal current from one reservoir to the other.
(ii) the ratio of the thermal current carried by the copper cube to that carried by the aluminium cube . thermal conductivity of copper is `401 Wm^(-1) K` and that of aluminium is `237 Wm(-1) K`.

View SolutionA wall consists of alternating blocks with length 'd' and coefficient of thermal conductivity `k_(1)` and `k_(2)`. The cross sectional area of the blocks are the same. The equivalent coefficient of thermal conductivity of the wall between left and right is

View SolutionA boiler is made of a copper plate `2.4mm` thick with an inside coating of a `0.2mm` thick layer of tin The surface area exposed to gases at `700^(@)C` is `400cm^(2)` The maximum amount of steam that could be generated per hour at atmospheric pressure is
`({:(K_(cu)=0.9cal//cm-s-^(0)&k_("tin"=0.15cal//cm/s/^(0)C),,,,),(andL_(steam)=540cal//g,,,,):})` .
View SolutionA lake surface is exposed to an atmosphere where the temperature is less than `0^(@)C`, if the thickness of the ice layer formed on the surface grows from 2 cm to 4 cm in 1 hour, the atomospheric temperature will be
(Thermal conductivity of ice, `K = 4 xx 10^(-3) cal cm^(-1) s^(-1) .^(@)C^(-1)` density of ice `= 0.9 g "cc"^(-1)`. Latent of density during of the state change. Assume that the water below the ice has `0^(@)C` temperature every where.)
View SolutionHeat flows radially outward through a spherical shell of outside radius `R_(2)` and inner radius `R_(1)`. The temperature of inner surface of shell is `theta_(1)` and that of outer is `theta_(2)`.The radial distance from centre of shell where the temperature is just half way between `theta_(1)` and `theta_(2)` is "
View SolutionA solid metallic sphere of diameter 20 cm and mass 10 kg is heated to a temperature of `327^@C` and suspended in a box in which a constant temperature of `27^@C` is maintained. Find the rate at which the temperature of the Sphere will fall with time. Stefan's constant`=5.67xx10^-8W//m^(2)//K^(4)` and specific heat of metal `=420J//kg//^(@)C`.
View SolutionWhich of the law can be understood in terms of Stefan's law
View SolutionA hot liquid is kept in a big room. According to Newton's law of cooling rate of cooling liquid (represented as y) is plotted against its temperature `T`. Which of the following curves may represent the plot?
View SolutionThree metal rods made of copper, aluminium and brass, each `20 cm` long `4cm` in diameter, are placed end to end with aluminium between the other two. The free ends of copper and brass are maintained at `100` and `0^(@)C` respectively. Assume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. The approximately equilibrium temperatures of the copper-aluminiu and aluminium-brass junctions are respectively.

View SolutionA closed cubical box is made of perfectly insulating material and the only way for heat to enter or leave the box is through two solid cylindrical metal plugs, each of cross sectional area `12cm^(2)` and length 8cm fixed in the opposite walls of the box. The outer surface of one plug is kept at a temperature of `100^(@)C` . while the outer surface of the plug is maintained at a temperature of `4^(@)C` . The thermal conductivity of the material of the plug is `2.0Wm^(-1)C^(-1)` . A source of energy generating 13W is enclosed inside the box. Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface.
View SolutionTwo models of a windowpane are made, two identical glass panes of thickness `3 mm` are separated with an air gap of `3mm`. This composite system is fixed in the window of a room. The other model consists of a single glass pane of thickness `6mm`, the temperature difference being the same as for first model. the ratio of the heat flow for the double pane to that for the single pane is `(K_("glass") = 2.5 xx 10^(-4) cal//s.m.^(@)C` and `K_("air") = 6.2 xx 10^(-6)cal//s.m.^(@)C)`
View SolutionHeat is flowing through two cylindrical rods of the same material. The diamters of the rods are in the ratio `1: 2` and the length in the ratio `2 : 1`. If the temperature difference between the ends is same then ratio of the rate of flow of heat through them will be
View SolutionThe ends of a metre stick are maintain at `100^(@)C` and `0^(@)C` . One end of a rod is maintained `25^(@)C` . Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
View SolutionA spherical solid blakc body of radius 'r' radiates power 'H' and its rate of cooling is 'C'. If density is constant then which of the following is/are true.
View SolutionTwo rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at `100^(@)C` and `0^(@)C` respectively. The temperature of the junction is `70^(@)C`. Then the temperature of the junction if the rods are inerchanged will be equal to `T^(@)C` Find `T`:
View SolutionFigure shows a steel rod joined to a brass rod. Each of the rods has length of `31 cm` and area of cross-section `0.20 cm^(2)`. The junction is maintained at a constant temperature `50^(@)C` and the two ends are maintained at `100^(@)C`. The amount of heat taken out from the cold junction in `10` minutes after the steady state is reached in `n xx 10^(2)J`. Find 'n' the thermal conductivities are `K_(steel) = 46 W//m-^(@)C` and `K_(brass) = 109 W//m-^(@)C`.

View SolutionConsider the situation shown in figure. The frame is made of the same material and has a uniform cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at `100^(@)C` is `130J` .
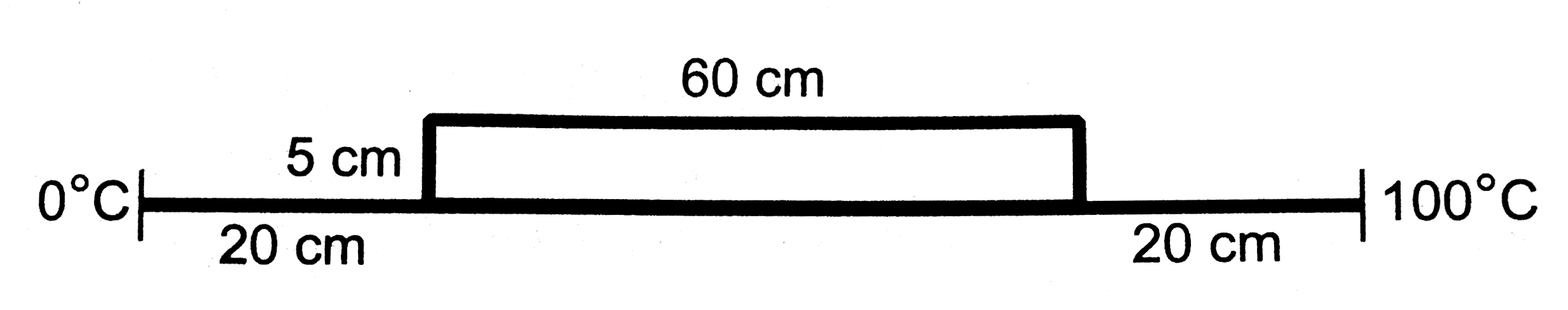
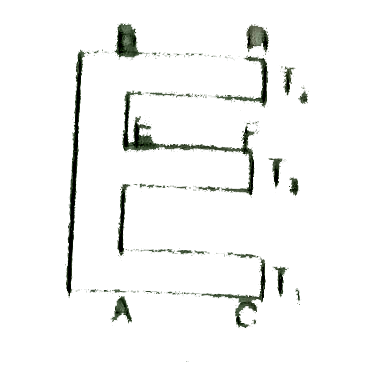
View SolutionFour thin identical rods `AB, AC, BD` and `EF` made of the same material are joined as shown. The free-ends `C,D` and `F` are maintained at temperature `T_(1),T_(2)` and `T_(3)` respectively. Assuming that there is no loss of heat of the surroundings, the temperature at joint `E` when the steady state is attained is `(1)/(K) (2T_(1)+2T_(2)+3T_(3))`. Find `K (E` is mid point of `AB)`
View SolutionOne end of a copper rod of uniform cross section and length 1.5 m is kept in contact with ice and the other end with water at `100^@C`. At what point along its length should a temperature of `200^@C` be maintained so that in the steady state, the mass of ice melting be equal to that of the steam produced in same interval of time. Assume that the whole system is insulated from surroundings:
`[L_("ice")=80 cal//g,L_("steam")=540 cal//g]`
View SolutionA hollow spherical conducting sheel of inner radius `R_(1) = 0.25 m` and outer radius `R_(2) = 0.50 m` is placed inside a heat reservoir of temperature `T_(0) = 1000^(@)C`. The shell is initially filled with water at `0^(@)C`. The thermal conductivity of the material is `k =(10^(2))/(4pi) W//m-K` and its heat capacity is negligible. The time required to raise the temperature of water to `100^(@)C is 1100K ln.(10)/(9) sec`. Find `K`. Take specific heat of water `s = 4.2 kJ//kg.^(@)C`, density of water `d_(w) = 1000 kg//m^(3) pi = (22)/(7)`

View SolutionA cylindrical rod of length 50cm and cross sectional area `1cm^(2)` is fitted between a large ice chamber at `0^(@)C` and an evacuated chamber maintained at `27^(@)C` as shown in figure. Only small protions of the rod are insid ethe chamber and the rest is thermally insulated from the surrounding. The cross section going inti the evacuted chamber is blackened so that it completely absorbe any radiation falling on it. The temperatuere of the blackened end is `17^(@)C` when steady state is reachhed. Stefan constant `sigma=6xx10^(-s)Wm^(-2)K^(-4)` . Find the thermal conductivity of the material of the rod.

View SolutionA spherical tungsten pieces of radius `1.0cm` is suspended in an evacuated chamber maintained at `300K`. The pieces is maintained at 1000K by heating it electrically. Find the rate at which the electrical energy must be supplied. The emissivity of tungsten is `0.30` and the Stefan constant `sigma` is `6.0xx10^(-s)Wm^(-2)K^(-4)` .
View SolutionAssume transmitivity `t rarr 0` for all the cases:
View SolutionA solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature.
View SolutionTwo bodies A and B have thermal emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are same. The two bodies emit total radiant power at the same rate. The wavelength `lambda_B` corresponding to maximum spectral radiancy from B is shifted from the wavelength corresponding to maximum spectral radiancy in the radiation from A by 1.0 `mum`. If the temperature of A is 5802 K, calculate (a) the temperature of B, (b) wavelength `lambda_B`.
View SolutionThe solar constant is the amount of heat energy received per second per unit area of a perfectly black surface placed at a mean distance of the Earth form the Sun, in the absence of Earth's atmosphere, the surface being held perpendicular to the direction of Sun's rays. Its value is `1388 W//m^(2)`. If the solar constant for the earth is 's'. The surface temperature of the sun is `TK,D` is the diameter of the sun, `R` is the mean distance of the Earth from the sun. The sun subtends a small angle 'theta' at the earth. Then correct options is/are:-
View SolutionA heated body emits radiation which has maximum intensity at frequency `v_(m)`. If the temperature of the body is doubled :
View SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities `K_(1) = 0.06 W // mK, K_(3) = 0.04 W// mK and K_(4) = 0.10 W// mK`. The layer thickness are `L_(1) = 1.5 cm, L_(3) = 2.8 cm and L_(4) = 3.5 cm`. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer `3 and 4` is:

View Solution
Figure shows in cros section a wall consisting of four layers with thermal conductivities `K_(1)=0.06W//mK`
`K_(3)=0.04W//mK` and `K_(4)=0.10W//mK`. The layer thicknesses are `L_(1)=1.5cm,L_(3)=2.8` cm and `L_(4)=3.5cm` the temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state.
Q. The temperature of the interface between layers 3 and 4 is
View SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities `K_(1) = 0.06 W//mK, K_(3) = 0.04 W//mK` and `K_(4) = 0.10 W//mK`. The layer thickness are `L_(1) = 1.5 cm, L_(3) = 2.8 cm` and `L_(4) = 3.5 cm`. The temperature of interfaces is as shown in figure. Energy transfer through the wall is steady.
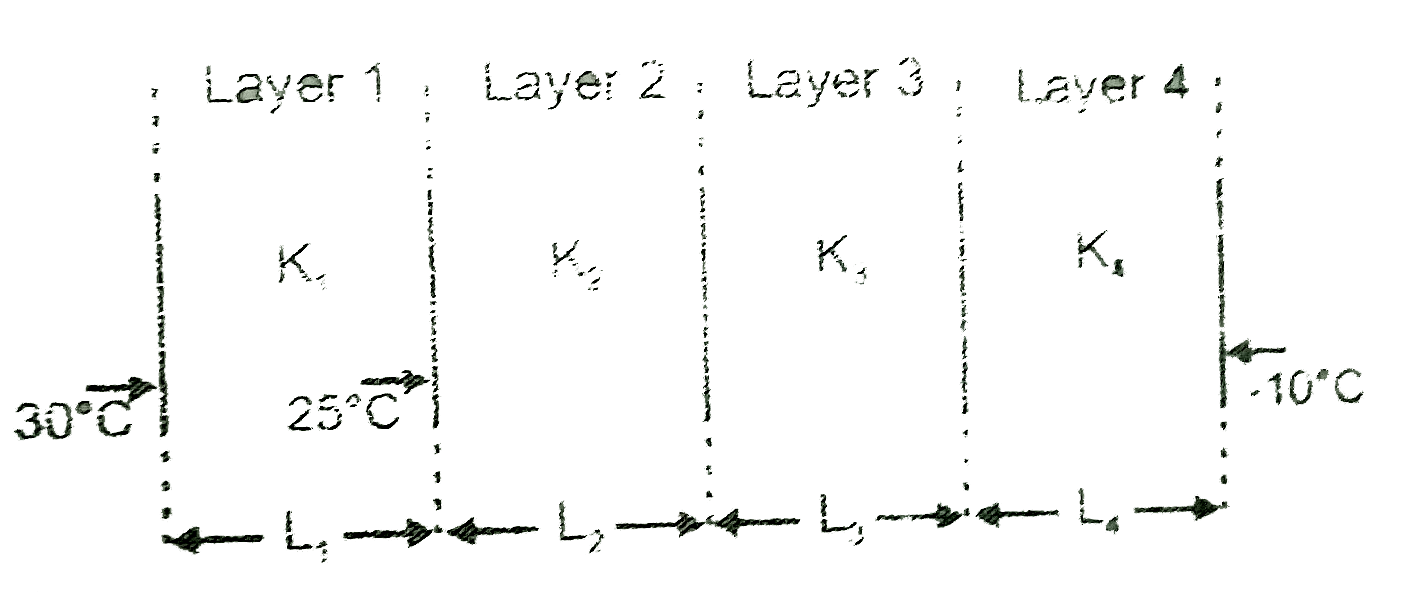
The temperature of the interface between layers `3` and `4` is:
View SolutionA body cools in a surrounding of constant temperature `30^@C` Its heat capacity is `2 J//^(@)C`. Initial temperature of cooling is valid. The body of mass 1 kg cools to `38^@C` in 10 min
When the body temperature has reached `38^@C`, it is heated again so that it reaches `40^@C` in 10 min. The heat required from a heater by the body is
View SolutionA body cools in a surrounding of constant temperature `30^@C` Its heat capacity is `2 J//^(@)C`. Initial temperature of cooling is valid. The body of mass 1 kg cools to `38^@C` in 10 min
When the body temperature has reached `38^@C`, it is heated again so that it reaches `40^@C` in 10 min. The heat required from a heater by the body is
View SolutionA body cools in a surrounding of constant temperature `30^@C` Its heat capacity is `2 J//^(@)C`. Initial temperature of cooling is valid. The body of mass 1 kg cools to `38^@C` in 10 min
When the body temperature has reached `38^@C`, it is heated again so that it reaches `40^@C` in 10 min. The heat required from a heater by the body is
View SolutionA metal ball of mass `2kg` is heated means of a `40W` heater in a room at `25^(@)C`. The temperature of the ball beomes steady at `60^(@)C`.
Find the rate of loss of heat to the surrounding when the ball is at `60^(@)C`.
View SolutionA metal ball of mass `2kg` is heated means of a `40W` heater in a room at `25^(@)C`. The temperature of the ball becomes steady at `60^(@)C`.
Find the rate of loss of heat to the surrounding when the ball is at `39^(@)C`.
View SolutionA metal ball of mass `2kg` is heated means of a `40W` heater in a room at `25^(@)C`. The temperature of the ball beomes steady at `60^(@)C`.
Assume that the temperature of the ball rises uniformly from `25^(@)C` to `39^(@)C "in" 2` minutes. Find the total loss of heat to the surrounding during this period.
View SolutionIn which of the following process convection of does not take place primarily ?
View SolutionA metal rod AB of length 10 x has its one end A in ice at `0^(@)C` and the other end B in water at 100°C. If a point P on the rod is maintained at 400°C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540 cal/g and latent heat of melting of ice is 80 cal/g. If the point P is at a distance of `lambdax` from the ice end A, find the value of `lambda` (Neglect any heat loss to the surroundings)
View SolutionTwo spherical bodies A (radius 6 cm) and B (radius 18 cm) are at temperature `T_(1)andT_(2)` respectively. The maximum intensity in the emission spectrum of A is at 500 nm and in that of B is at 1500 nm. Considering them to be black bodies, what will be the ratio of the rate of total energy radiated by A to that of B?.
View SolutionA composite block is made of slabs A,B,C,D and E of different thermal conductivities (given in terms of a constant K and sizes (given in terms of length, L) as shown in the figure. All slabs are of same width. Heat 'Q' flows only from left to right through the blocks. Then in steady state
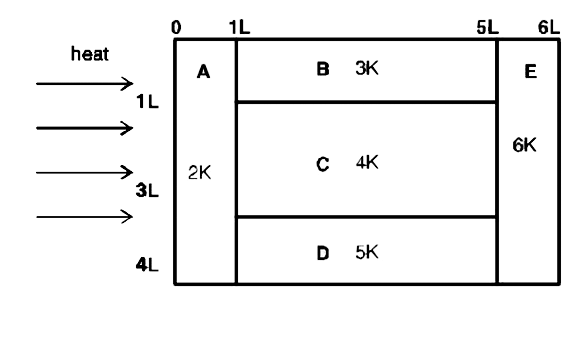
View SolutionThree very large plates of same area are kept parallel and close to each other. They are considered as ideal black surfaces and have very high thermal conductivity. The first and third plates are maintained at temperature 2T and 3T respectively. The temperature of the middle (i.e. second) plate under steady state condition is
View SolutionTwo rectangular blocks, having identical dimensions, can be arranged either in configuration I or in configuration II as shown in the figure. One of the blocks has thermal conductivity k and the other 2 k. The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9 s to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the configuration II is :

View SolutionParallel rays of light of intensity `I=912Wm^(-2)` are incident on a spherical black body kept in surroundings of temperature 300 K. Take Stefan’s constant `sigma=5.7xx10^(-8)Wm^(-2)K^(-4)` and assume that the energy exchange with the surrounding is only through radiation. The final steady temperature of the black body is close to
View SolutionTwo spherical stars A and B emit black body radiation. The radius of A is 400 times that of B and A emits `10^(4)` times the power emitted from B. The ratio `(lambda_(A)//lambda_(B))` of their wavelengths `lambda_(A)` and `lambda_(B)` at which the peaks oc cur in their respective radiation curves is :
View SolutionThe figure shows a system of two concentric spheres of radii r 1 and r 2 and kept at temperature T 1 and T 2 , respectively. The radial rate of flow of heat in a substance between the two concentric spheres, is proportional to:
View SolutionAssuming the sun to have a spherical outer surface of radius r, radiating like a black body at temperature `t^(@)C`, the power received by a unit surface, (normal to the incident rays) at distance R from the centre of the Sun is:-
Where `sigma` is the Stefan's Constant.
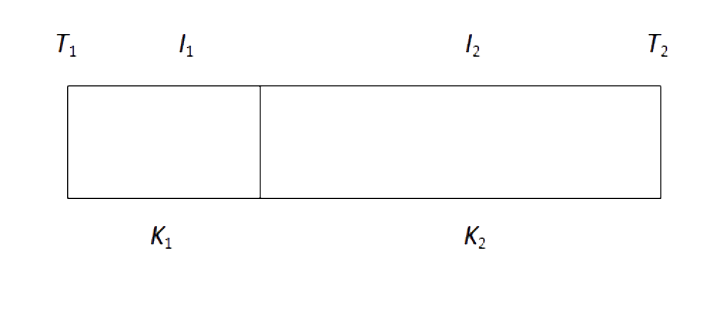
View SolutionOne end of a thermally insulated rod is kept at a temperature `T_(1)` and the other at `T_(2)`. The rod is composed of two sections of lengths `l_(1) and l_(2)` and thermal conductivities `K_(1) and K_(2)` respectively. The temperature at the interface of the two sections is
View SolutionA long metallic bar is carrying heat from one its ends to the other end under steady-state. The variation of temperature `theta` along the length x of the bar from its end is best described by which of the following figure.
View SolutionIf a piece of metal is heated to temperature `theta` and then allowed to cool in a room which is at temperature `theta_(0)` the graph between the temperature T of the metal and time t will be closest to :
View SolutionThree rods of Copper, Brass and Steel are welded together to from a Y - –shaped structure. Area of cross – section of each rod `= 4 cm^(2)`. End of copper rod is maintained at `100^(@)C` where as ends of brass and steel are kept at `0^(@)C`. Lengths of the copper, brass and steel rods are 46, 13 and 12 cms respectively. The rods are thermally insulated from surroundings except at ends. Thermal conductivities of copper, brass and steel are 0.92, 0.26 and 0.12 CGS units respectively. Rate of heat flow through copper rod is :
View SolutionThe two ends of a rod of length L and a uniform cross -secontional area A are kept at two temperatures `T_(1)` and `T_(2) (T_(1) gt T_(2))`. The rate of heat tranfer, `(dQ)/(dt)`, through the rod in a steady state is given by
View SolutionA cylindrical rod having temperature `T_1` and `T_2` at its end. The rate of flow of heat `Q_1` cal/sec. If all the linear dimension are doubled keeping temperature remain const. then rate of flow of heat `Q_2` will be : -
View SolutionA wall has two layers A and B, each made od=f different material. Both the layers have the same thickness. The thermal conductivity for A is twice that B and, under steady condition, the temperature difference across the wall is `36^(@)`C. The temperature difference across the layer A is
View Solution
All the rods have same conductance `K` and same area of cross section A. if ends A and C are maintained at temperature `2T_(0)` and `T_(0)` respectively then which of the following is/are correct
View SolutionConsider two rods of same length and different specific heats (`S_1, S_2`), conductivities (`K_1, K_2`) and area of cross-sections (`A_1, A_2`) and both having temperature `T_1 and T_2` at their ends. If rate of loss of heat due to conduction is equal, then :-
View SolutionTwo plates each of area A, thickness `L_1 and L_2` thermal conductivities `K_1 and K_2` respectively are joined to form a single plate of thickness `(L_1+L_2)`. If the temperatures of the free surfaces are `T_1 and T_2`. Calculate.

(a) rate of flow of heat
(b) temperature of interface and
(c) equivalent thermal conductivity.
View SolutionConsider a composite slab consisting of two different materials having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View SolutionA square is made of four rods of same material one of the diagonal of a square is at temperature difference `100^@C`, then the temperature difference of second diagonal:
View SolutionIf the temperature difference on the two sides of a wall increases from `100^(@) C` to `200^(@)C`, its thermal conductivity
View SolutionThe colour of a star indicates its
View SolutionThe means of energy transfer in vacuum is:
View SolutionWhich of the following is nearest to blackbody-
View SolutionWhich of the following is true statement?
View SolutionFor a black body at temperature `727^(@)C`. If the temperature of the black body is changed to `1227^(@)C`, then its radiating power will be
View SolutionAccording to Wien's law
View SolutionIf `lambda_(m)` denotes the wavelength at which the radiative emission from a black body at a temperature T K is maximum, then
View SolutionA black body at `1227^(@)C` emits radiations with maximum intensity at a wavelength of 5000 A. If the temperature of the body is increased by `1000^(@)C`, the maximum intensity will be observed at:
View SolutionThe energy radiated by a black body is directly proportional to :
View SolutionIf temperature becomes double, the emitted radiation will be :
View SolutionPrevost's theory of heat exchange tells that a body radiates thermal energy-
View SolutionReflection and absorption coefficient of a given surface at `0^@C` for a fixed wavelength are 0.5 (each). At the same temperature and wavelength the transmission (coefficient) of surface will be-
View SolutionA black metal foil is warmed by radiation from a small sphere at temperature 'T' and at a distance d'. It is found that the power received by the foil is P. If both the temperature and distance are doubled, the power received by the foil will be
View SolutionA body takes 10 min to cool douwn from `62^@C` to `50^@C`. If the temperature of surrounding is `26^@C` then in the next 10 minutes temperature of the body will be
View SolutionTwo circular disc `A` and `B` with equal radii are blackened. They are heated to same temperature and are cooled under identical conditions. What inference do your draw from their cooling curves?

View SolutionAccording to Newton’s law of cooling, the rate of cooling of a body is proportional to `(Deltatheta)^(n)` , where `Deltatheta`is the difference of the temperature of the body and the surrounding, and n is equal to :
View Solution
Exercise questions and complete solutions for chapter HEAT TRANSFER of RESONANCE ENGLISH of Class 11