Complete Solutions to Exercise of chapter NEWTONS LAWS OF MOTION AND FRICTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION AND FRICTION |
| RESONANCE | Exercise |
| Number Of Questions | 56 |
| Academic Year | 2023-24 |
Two blocks A and With mass 4 kg and 6 kg respectively are connected by a stretched spiring of negligible mass as in figure. When the two blocks are released simultaneously the initial acceleration of B is `1.5 m//s^(2)` westward. The acceleration of A is :

View SolutionA body of mass `32 kg` is suspended by a spring balance from the roof of vertically operating lift and going downwards from rest. At the instant the lift has covered 20 m and 50 m, the spiring balance showed 30 kg and 36 kg respectively. The velocity of the lift is
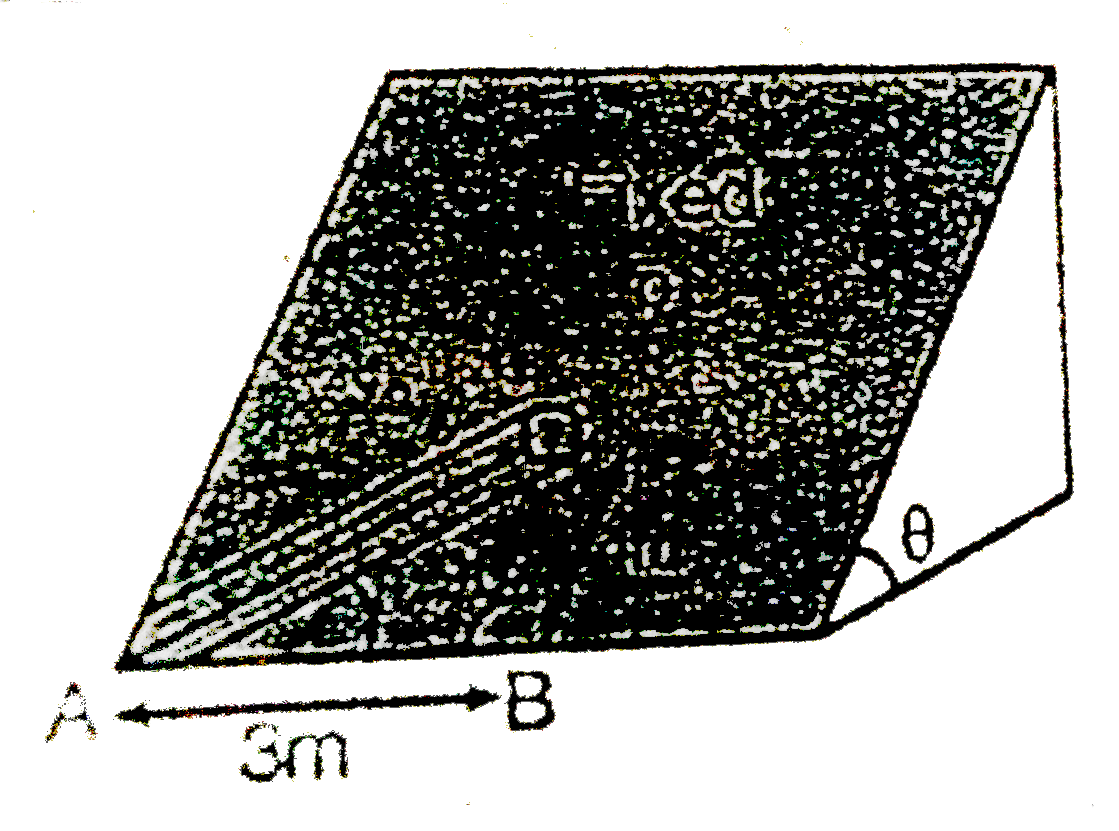
View SolutionThere is inclined surface of inclination `theta=30^(@)`. A smooth groove is cut into it forming angle `alpha` with AB. A steel ball is free to slide along the groove. If the ball is released from the point O at top end of the groove, the speed when it comes to A is `[g=10 m//s^(2)`]
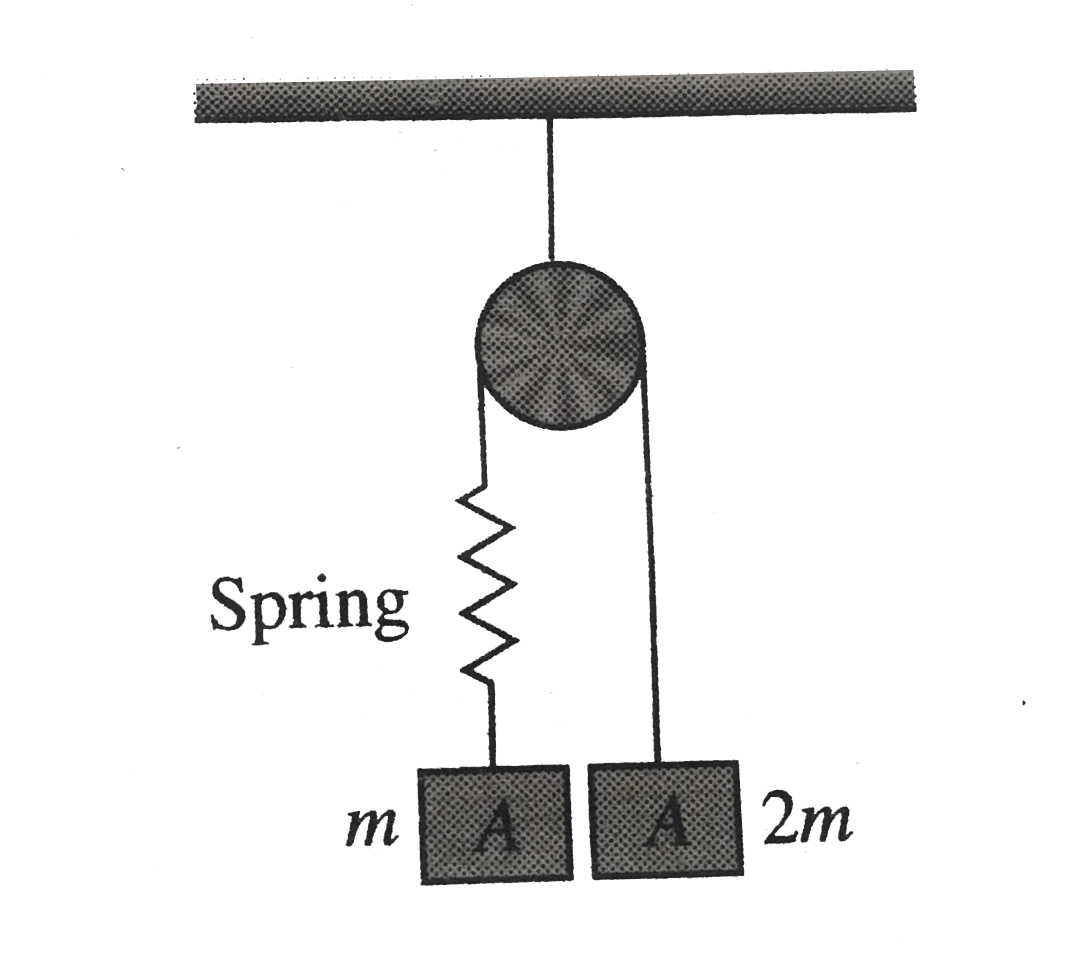
View SolutionTwo blocks A and B of masses m and 2m, respectively , are held at rest such that the spring is in natural length. Find out the acceleration of both the blocks just after relese.
View SolutionA uniform rope of length L and mass M is placed on a smooth fixed wedge as shown. Both ends of the rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initiate acceleration of rope is
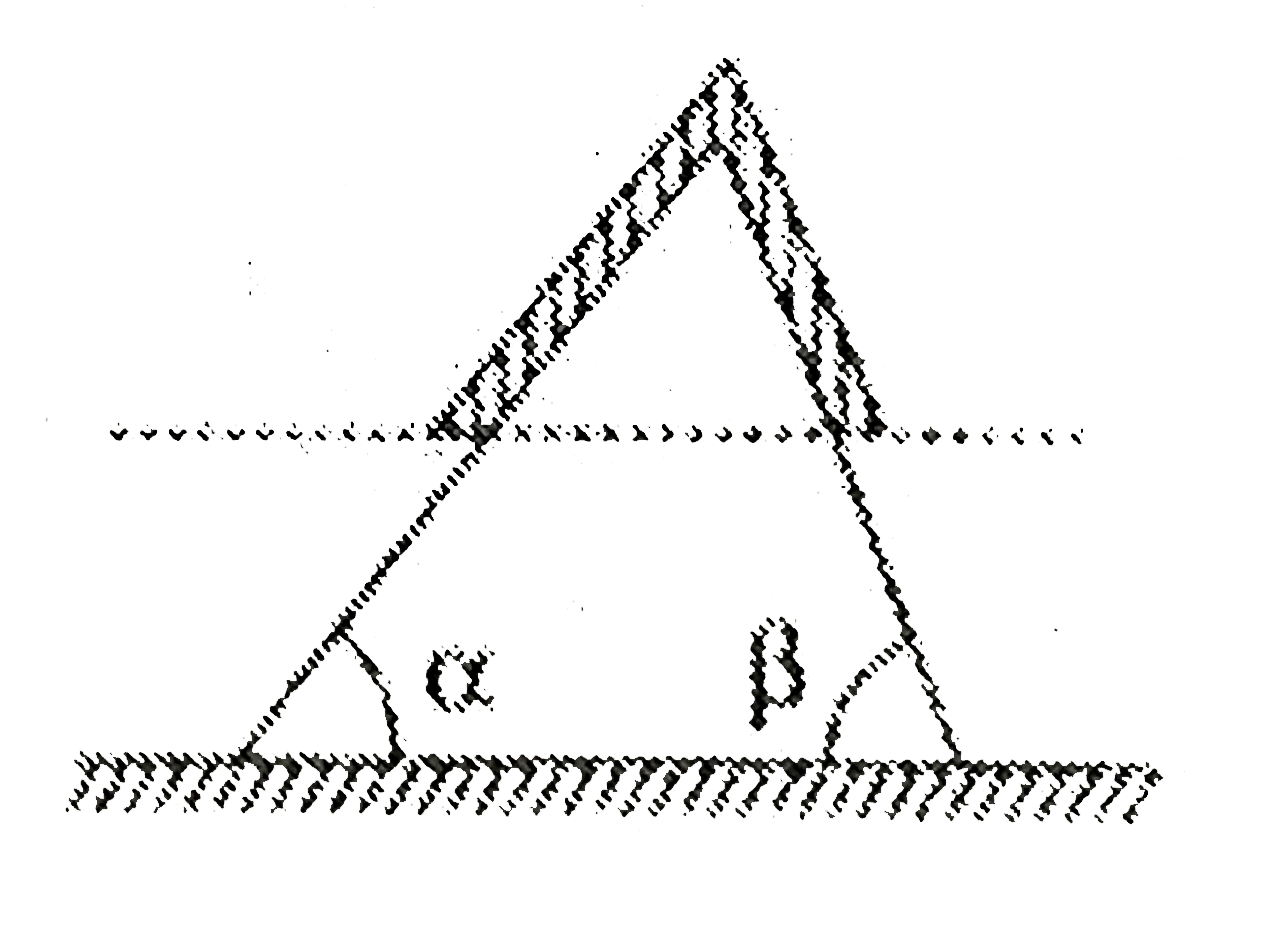
View SolutionA bob is hanging over a pulley inside a car through a string. The second end of the string is in the hands of a person standing in the car. The car is moving with constant acceleration a directed horizontally as shown in fig. The other end of the string is pulled with constant acceleration a vertically. The tension in the string is equal to

View SolutionA spring of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp at the time of equilibrium is given by
View SolutionThe system shown is hanging in equilibrium above the ground. When the string is cut at t=0. The time at which the spring is at its natural length will be (Take `pi^(2)`=10)
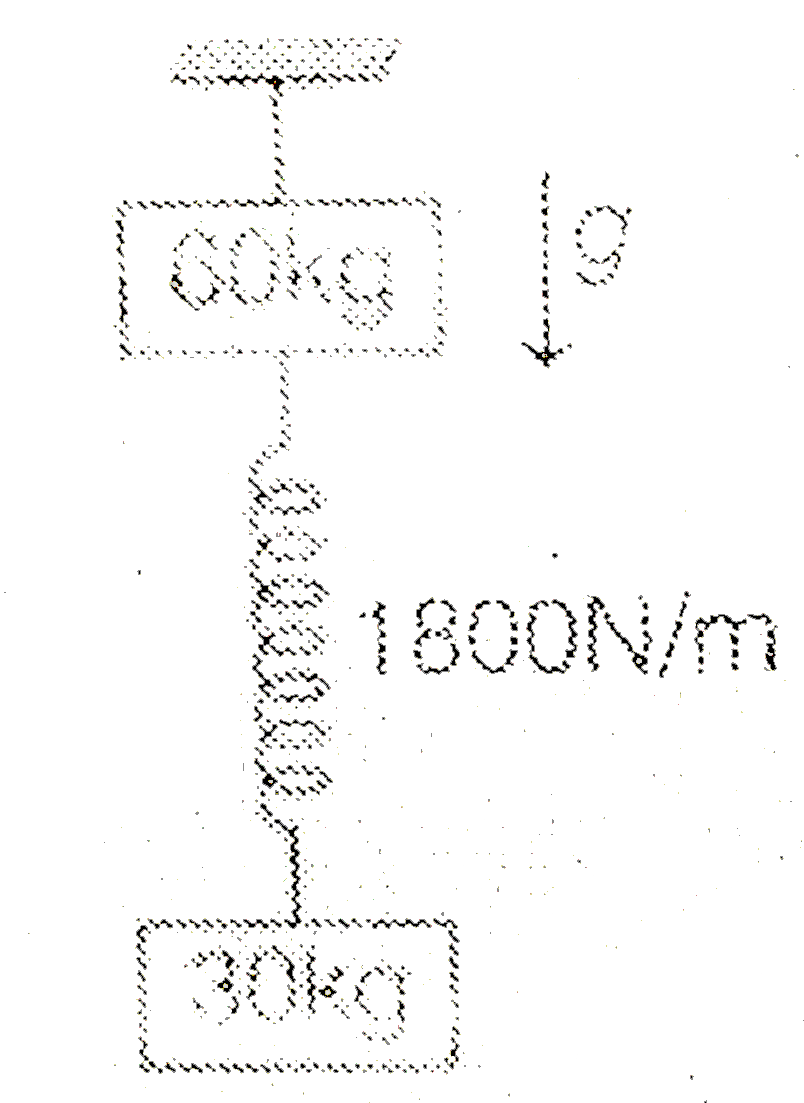
View SolutionTwo identical small masses each of mass m are connected by a light inextensible string on a smooth horizontal floor. A constant force F is applied at the mid point of the string as shown in fig. find the acceleration of each mass towards each other.

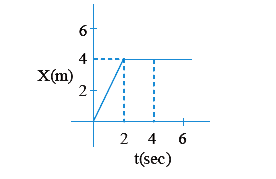
View SolutionIn the figure, the position time graph of a particle of mass 0.1 kg is shown. The impulse at t=2 second is `:`
View SolutionA man is standing on a sparing platform, Reading of spring balaance is `60kg` wt If man jumps outside the platform then the reading of the spring balance .
View Solution
Figure shows a 5 kg ladder hanging from a string that is connected with a ceiling and is having a spring balance connected in between. A boy of mass 25 kg is climbing up the ladder at acceleration `1(m)/(s^2)`. Assuming the spring balance and the string to be massless and the spring to show a constant reading, the reading of thespring balance is: (Take`g=10(m)/(s^2)`)
View SolutionA ball of mass 3kg moving with a speed of 100 m/s, strikes a wall at an angle `60^(@)` (as shown in figure). The ball rebounds at the same speed and remains in contact with the wall for 0.2 s, the force exerted by the ball on the wall is

View SolutionA block of mass 4 kg is suspended through two light spring balances A and B is series. Then A and B will read respectively.
View SolutionTwo masses `m_(1)` and `m_(2)` which are connected with a light string, are placed over a frictionless pulley. This set up is placed over a weighing machine, as shown. Three combination of mass `m_(1)` and `m_(2)` are used, in first case `m_(1) =6kg` and `m_(2)=2 kg`, in seconds case `m_(1)=5 kg` and `m_(2)=3 kg` and in third case `m_(1)=4 kg` and `m_(2)= 4 kg`. masses are held stationary initially and then released. if the reading of the weighing machine after the release in three cases are `W_(1),W_(2)` and `W_(3)` respectively then:
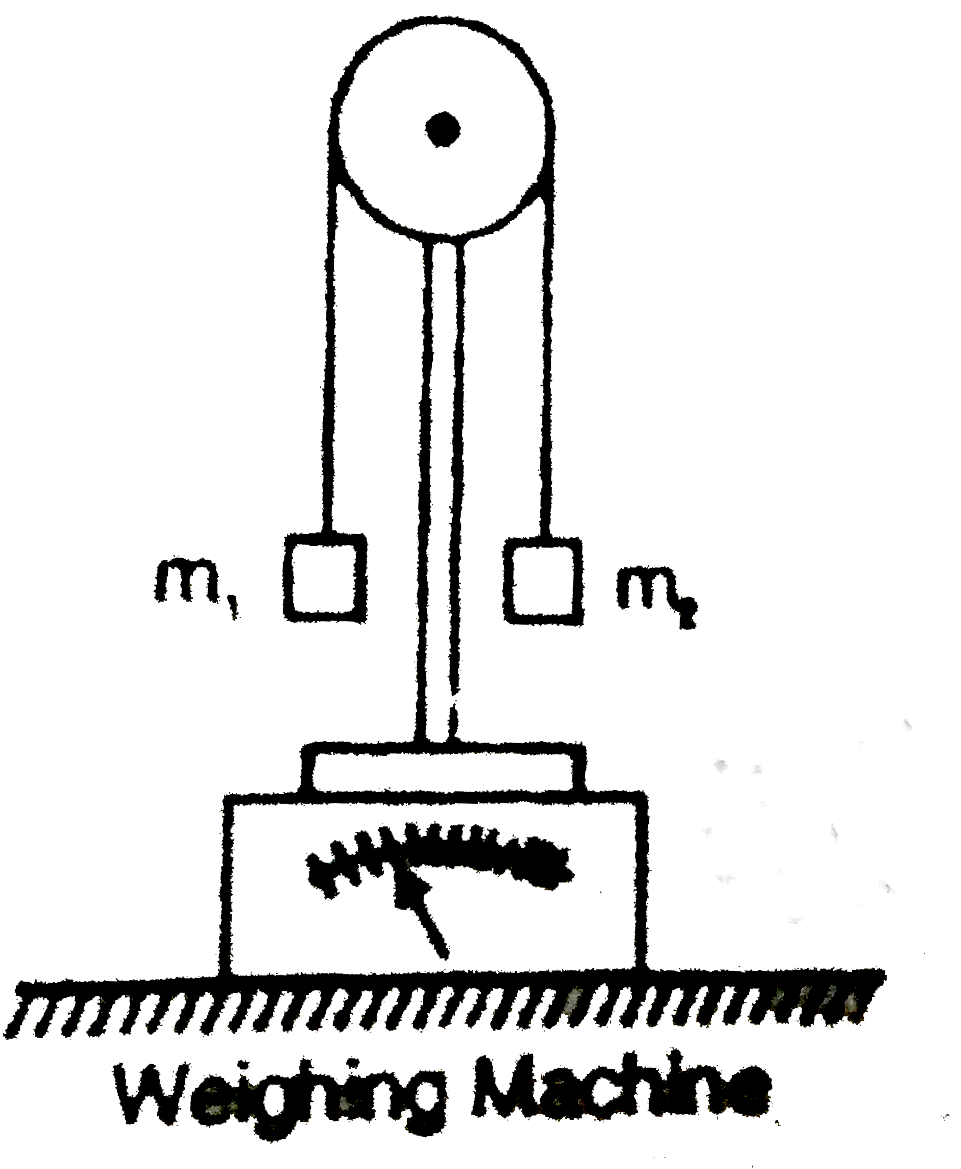
View SolutionA wooden block and a metal coin are connected by a string as shown in figure. Both have same volume and both are placed in a beaker of water. Now the beaker is given acceleration towards right, then the string will tilt towards

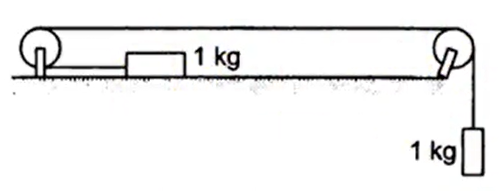
View SolutionCalculate the tension in the string shown in figure. The pulley and the string are light and all surfaces are frictionless. Take g=10 m/`s^2`.
View SolutionThe elevator shown in figure is descending with an acceleration of `2m/s^2`. The mass of the block A is 0.5 kg. What force is exerted by the block A on the block B?
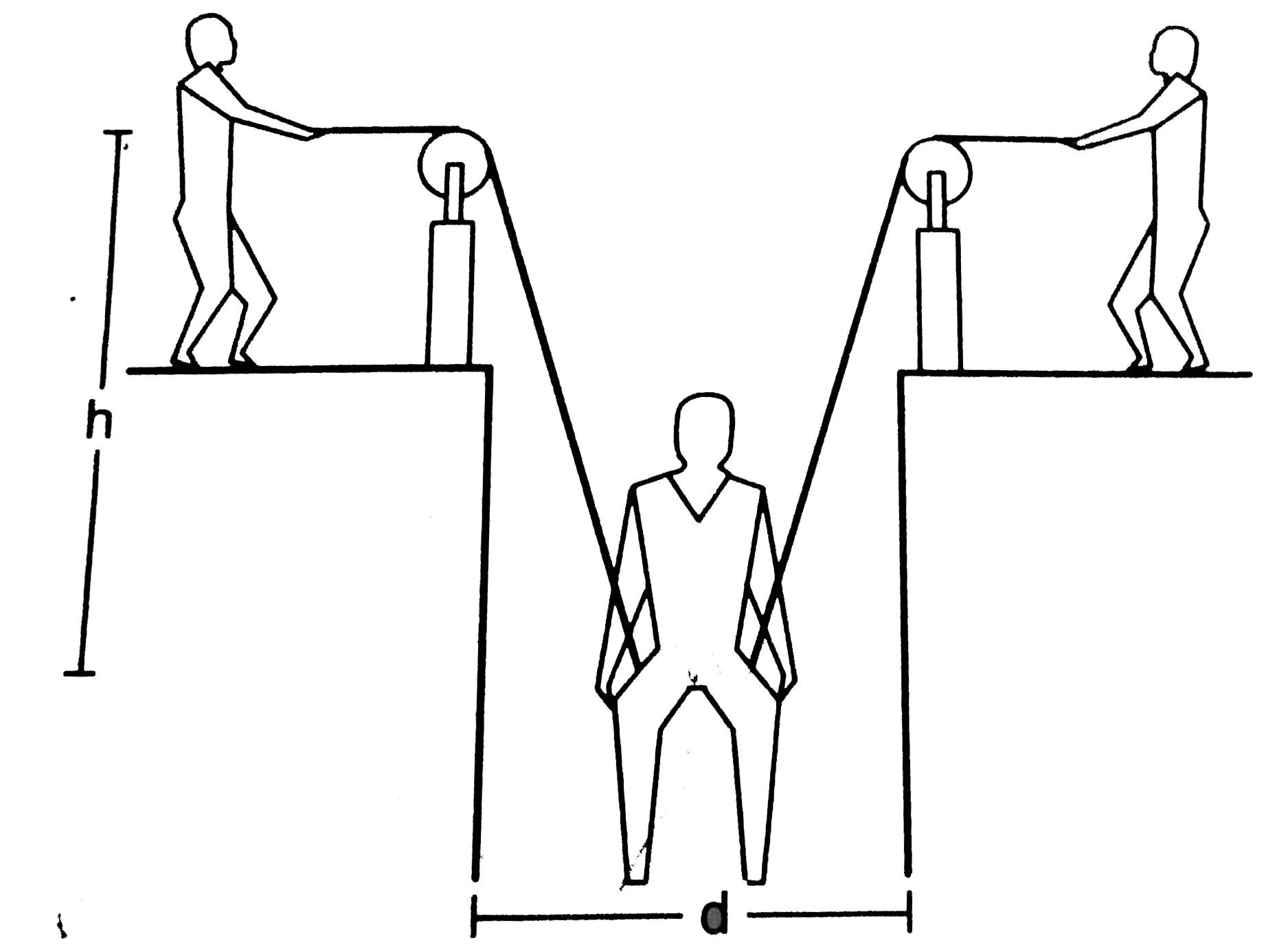
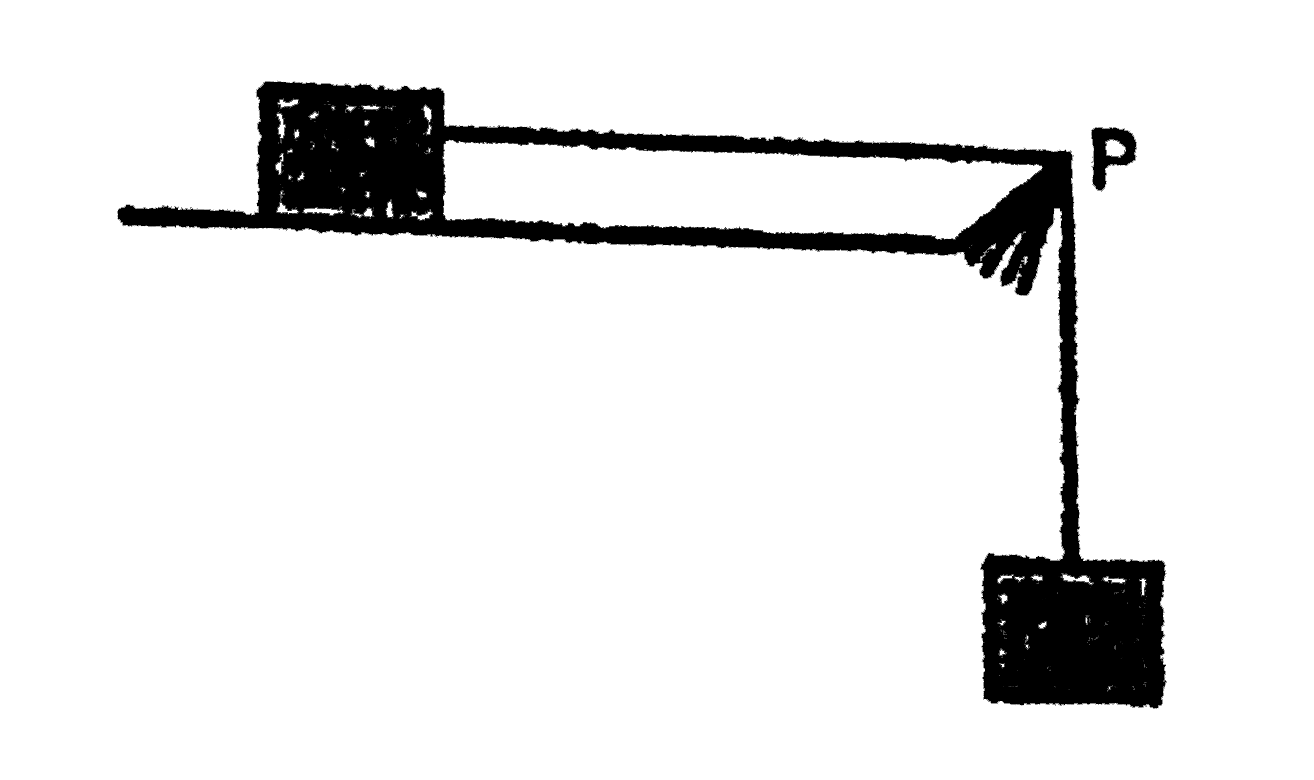
View SolutionIn fig., a person wants to rise a block lying on the ground to a height h. In both the cases, if the time required is same, then in which case he has to exert more force? Assuem pulleys and strigns light.
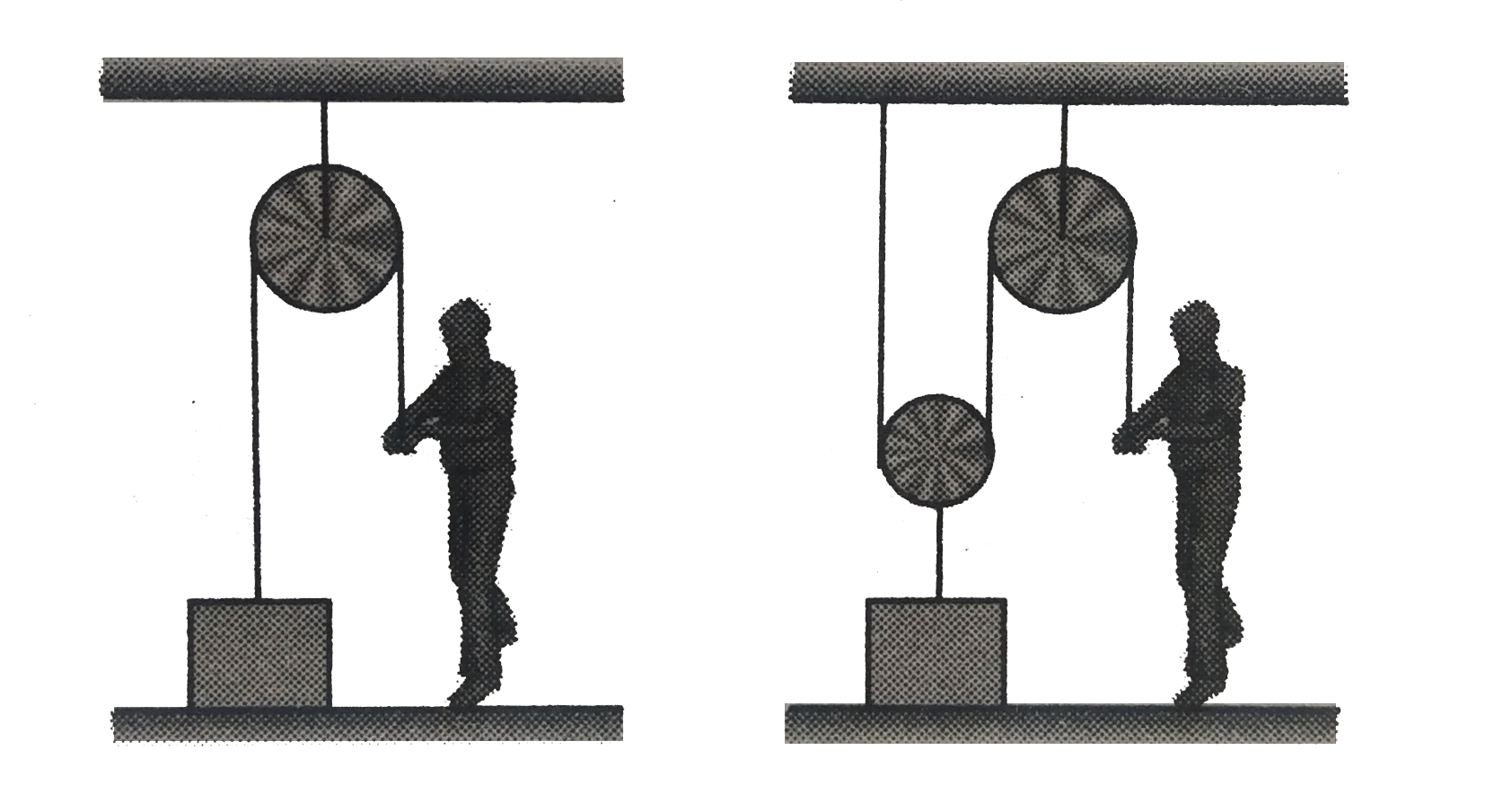
View SolutionBlocks of mass `M_(1)` and `M_(2)` are connected by a cord which passes over the pulleys `P_(1)` and `P_(2)` as shown in the figure. If there is no friction , the acceleration of the block of mass `M_(2)` will be `:`
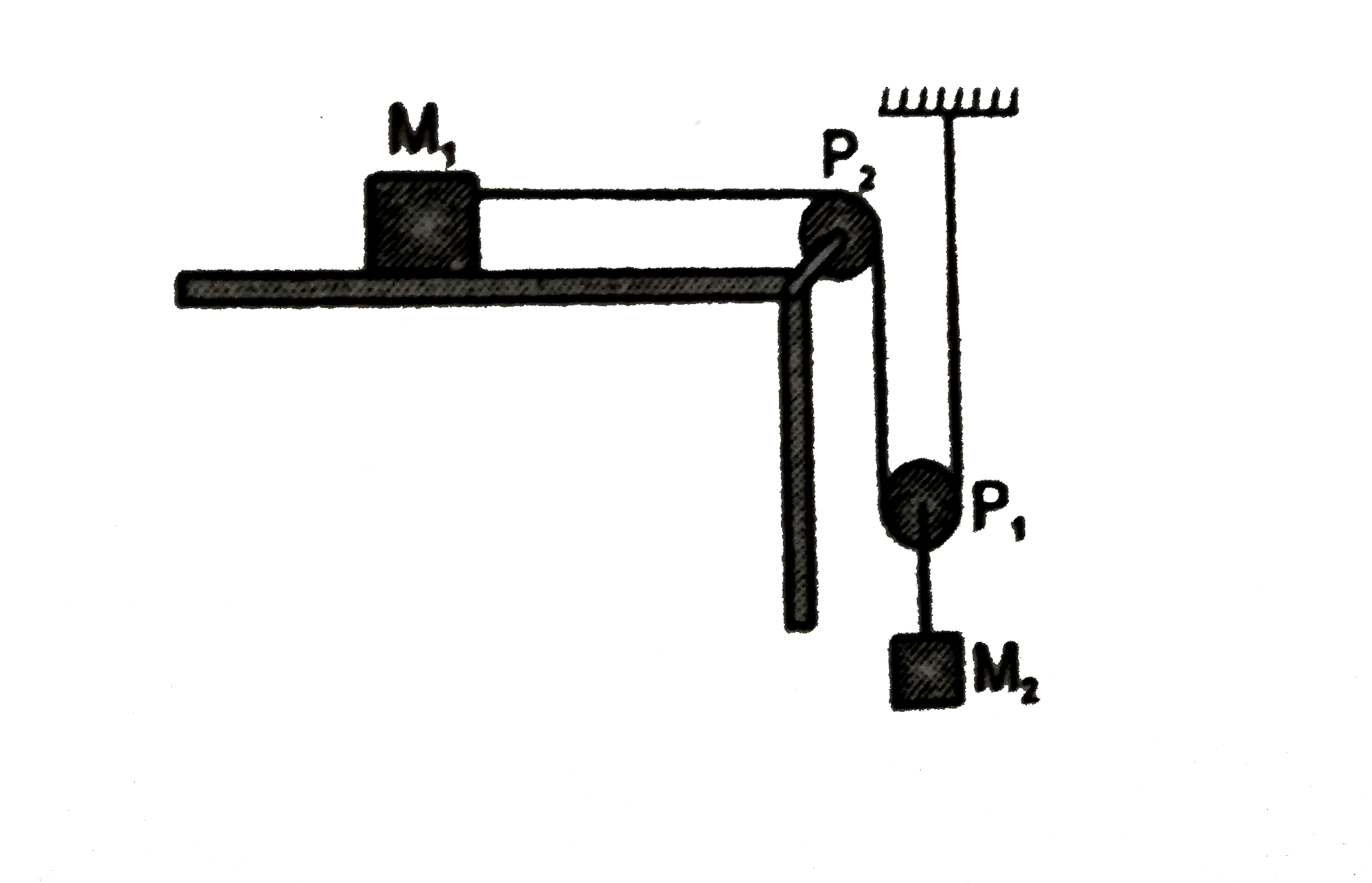
View SolutionA painter of mass M stands on a platforms of mass m and pulls himself up by two ropes which hang over pulley as shown in fig. He pulls each rope with force F and moves upward with uniform acceleration a, find a (neglecting the fact that no one could do this for long time).

View SolutionOne end of massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum vertical force that the clamp can bear is 360 N. With what value of minimum safe acceleration ( in `ms^(-2)`) can a man of 60 kg climp down the rops ?
View SolutionThe vertical displacement of a block A in meter is given by `y=t^(2)//4` where t is in second. The downward acceleration `a_(B)` of a block B ( in `m//s^(2)`) is

View SolutionA metal sphere I hung by a string fixed to a wall. The forces acting on the sphere are shown in fig. Which of the following statements is `//` are correct ?
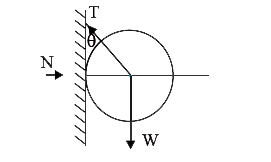
(a) `N+T+ W =0`
( b) `T^(2) = N^(2) + W^(2)`
( c ) `T = N + W `
(d) `N = W tan theta `
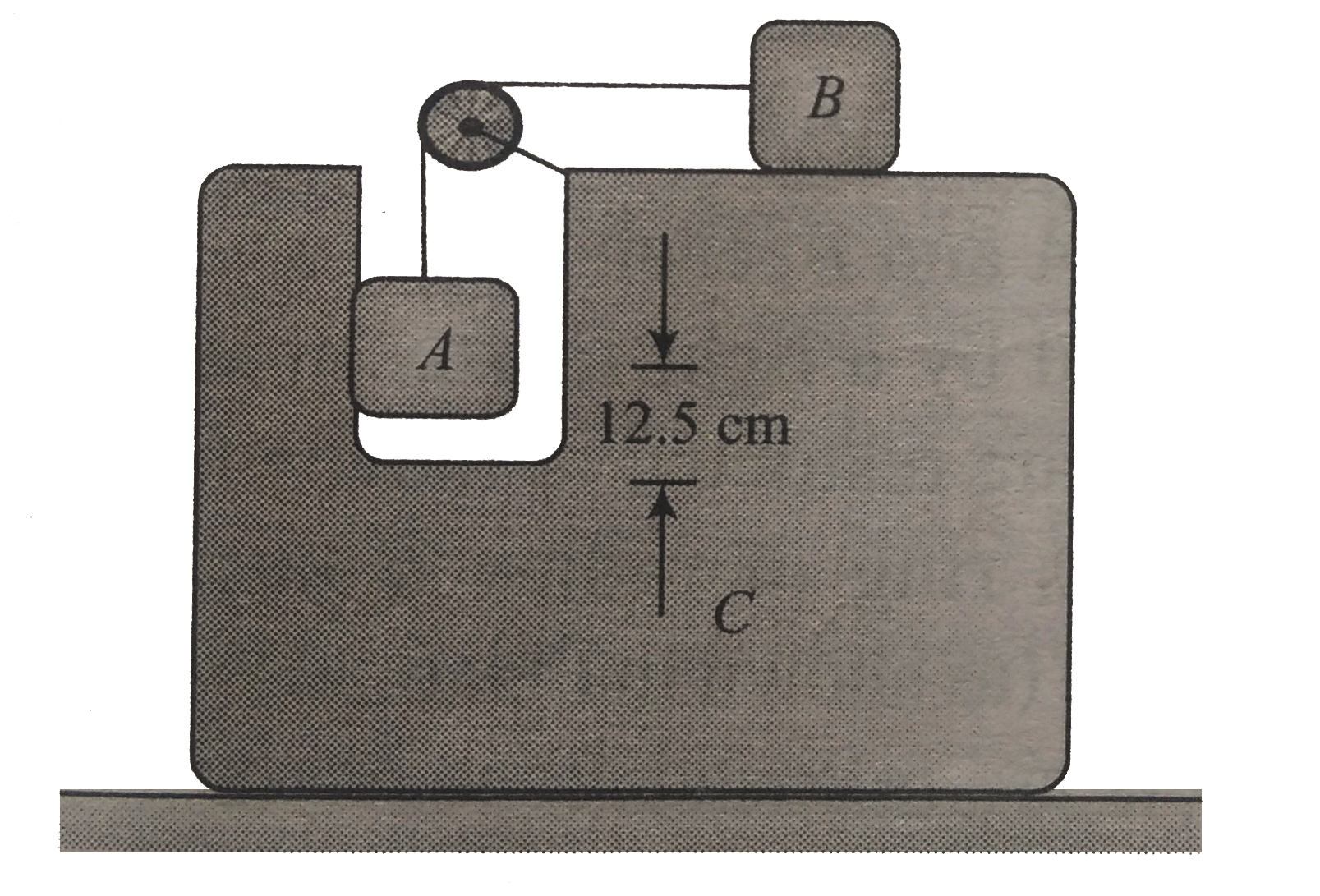
View SolutionA small, light pulley is attached with a block C of mass 4 kg as shown in fig. Block B of mass 1.5 kg is placed on the top horizontal surface of C. Another block A of mass 2 kg is hanging from a string, attached with B and passing over the pulley. Taking `g=10ms^(-2)` and neglecting friction, calculate the acceleration of each block when the system is released from rest.
View SolutionA perfectly straight portion of a uniform rope has mass m and length L. At end A of the segment. The tension in the rope is `T_(A)` and at end B it is `T_(B)(T_(B) gt T_(A))` Neglect effect of gravity and no contact force acts on the rope in between points A and B. the tension in the rope at a distance L/5 from end A is
View SolutionThree equal weight `A,B` and `C` of mass `2kg` each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights `B` and `C` is approximately

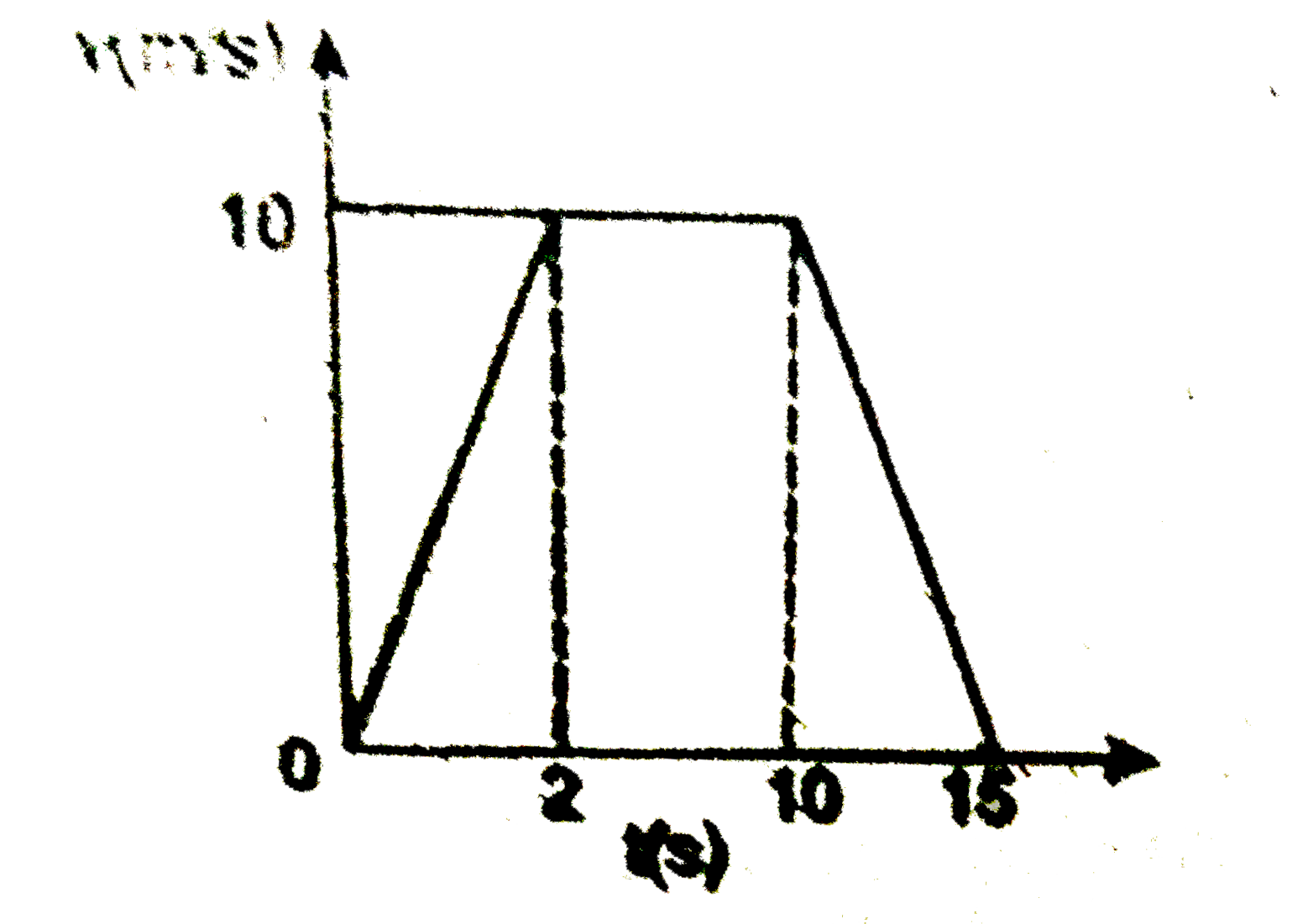
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be `(g=10 m//s^(2))`
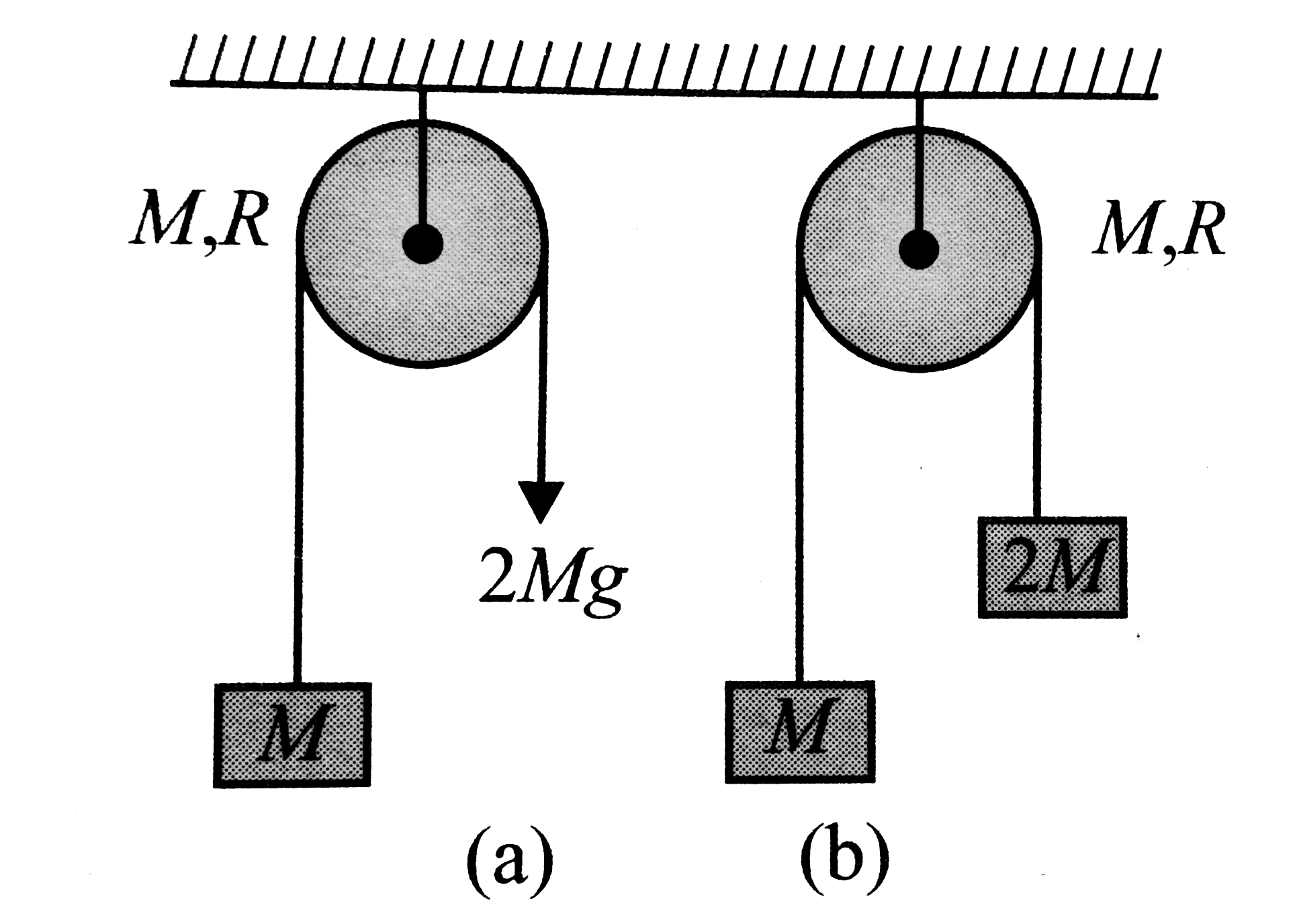
View SolutionA cord is wrapped on a pulley (disk) of mass `M` and radius `R` as shown in Fig. To one end of the cord, a block of mass `M` is connected us shown and to other end in (a) a force of `2 Mg` and in (b) a block of mass `2M`. Let angular acceleration of the disk in `A` and `B` is `alpha_(A)` and `alpha_(B)`, respectively, then (cord is not slipping on the pulley).
View SolutionA person is standing in an elevator. In which situation he finds his weight less than actual when:
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. the weight of the block is `(g=10 m//s^(2))`

View SolutionA block `A` of mass `4 kg` is kept on ground. The coefficient of friction between the block and the ground is `0.8`. The external force of magnitude `30 N` is applied parallel to the ground. The resultant force exerted by the ground on the block is `(g = 10 m//s^(2))` a) 40 N b) 30 N c) zero d) 50 N
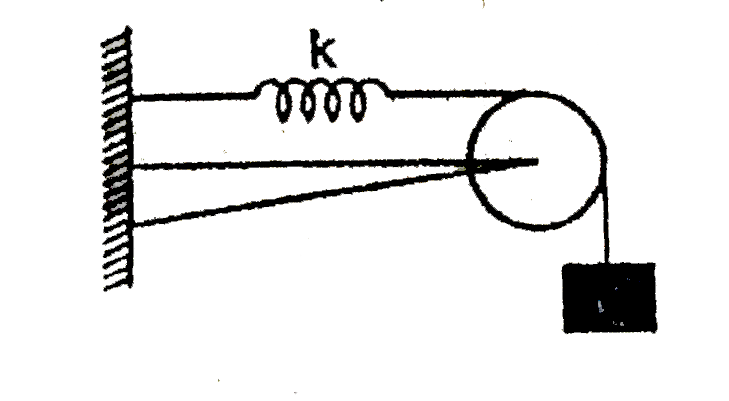
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move?
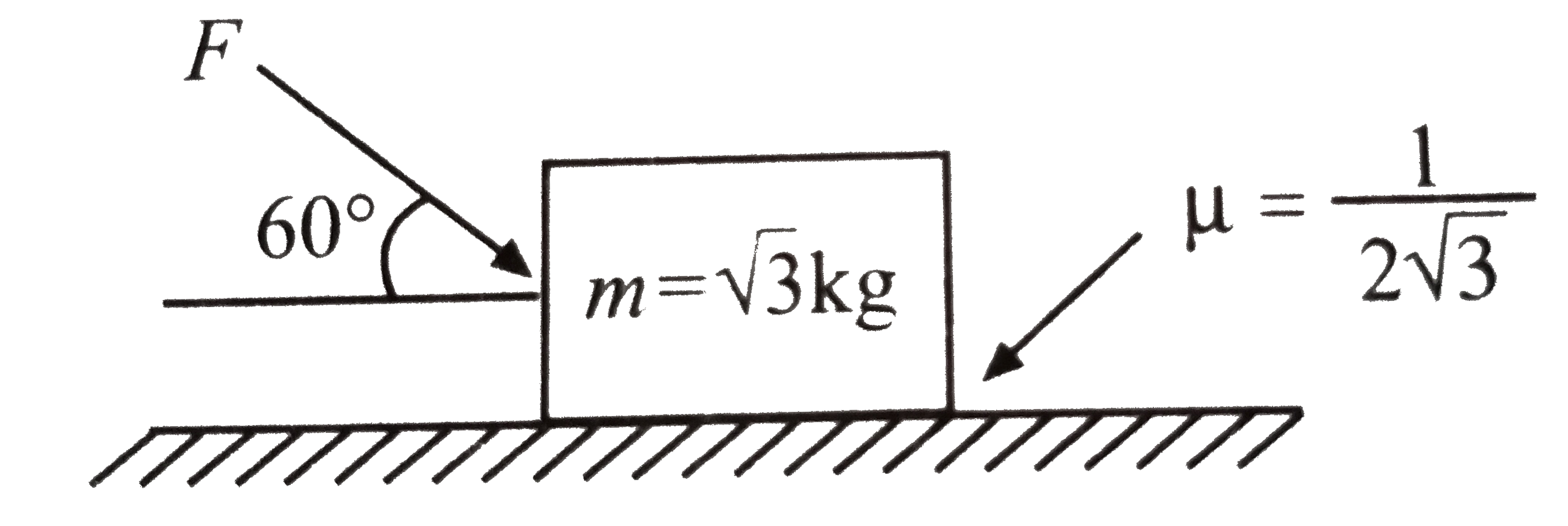
View SolutionAn external force of 6N is applied on body at rest at time t=0, at t=1 sec direction of force is reversed. Find the speed of body when it comes back to the initial position

View SolutionIf the coefficient of friction between `A` and `B` is `mu`, the maximum acceleration of the wedge `A` for which `B` will remain at rest with respect to the wedge is
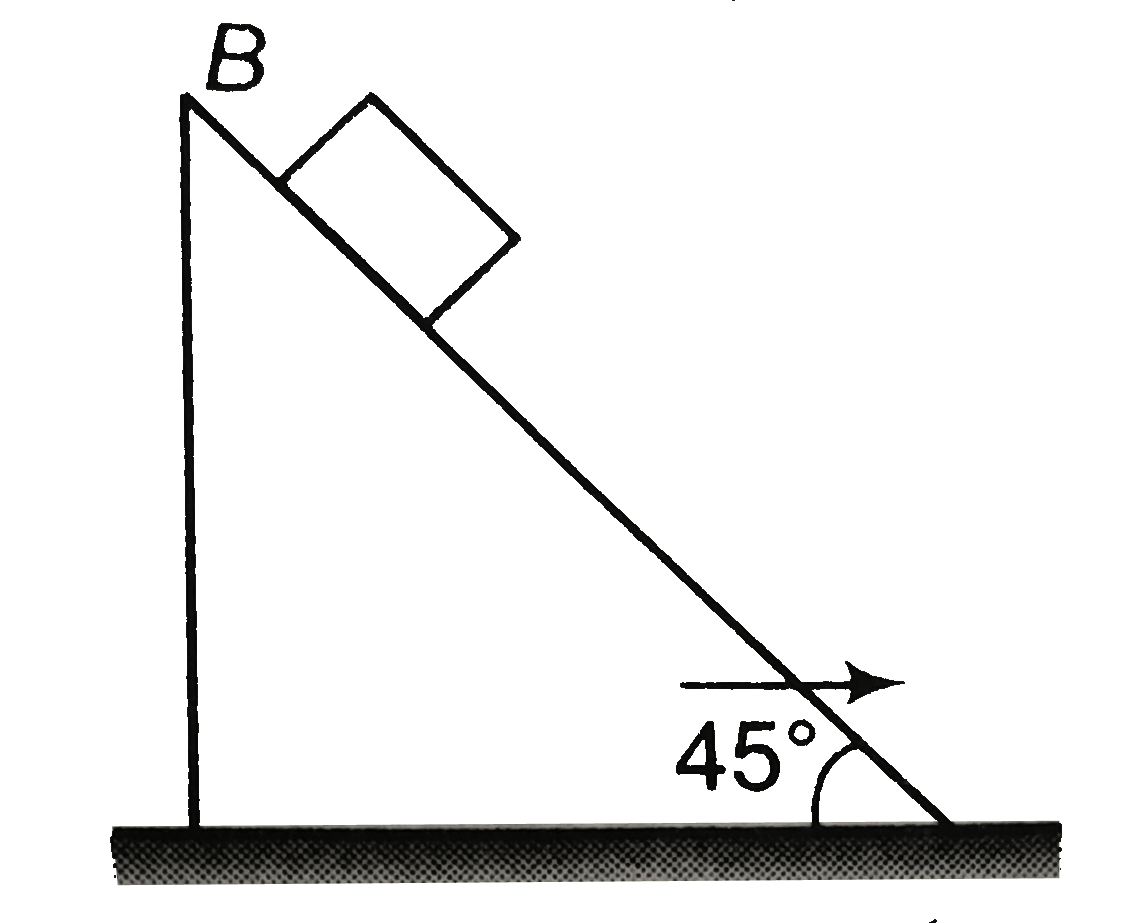
View SolutionA block of mass 5 kg and surface area `2m^(2)` just begins to slide down an inclined plane when the angle on inclination is `30^(@)`. Keeping mass same, the surface area of the block is doubled. The angle is which this starts sliding down is
View SolutionA smooth block is released at rest on a `45^(@)` incline and then slides a distance d. The time taken to slide is n times as much to slide on rough incline than on a smooth incline. The coefficient of friction is `:`
View SolutionFigure shows a block kept on a rough inclined plane. The maximum external force along the plane downwards for which the block remains at rest is 1N while the maximum external force along the incline upwards for which the block is rest is 7N. The coefficient of static friction `mu` is

View Solution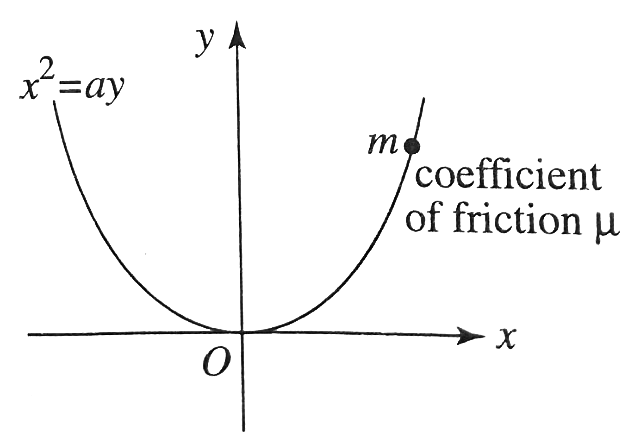
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is `x^2=ay`. If the coefficient of friction is `mu`, the highest distance above the x-axis at which the particle will be in equilibrium is
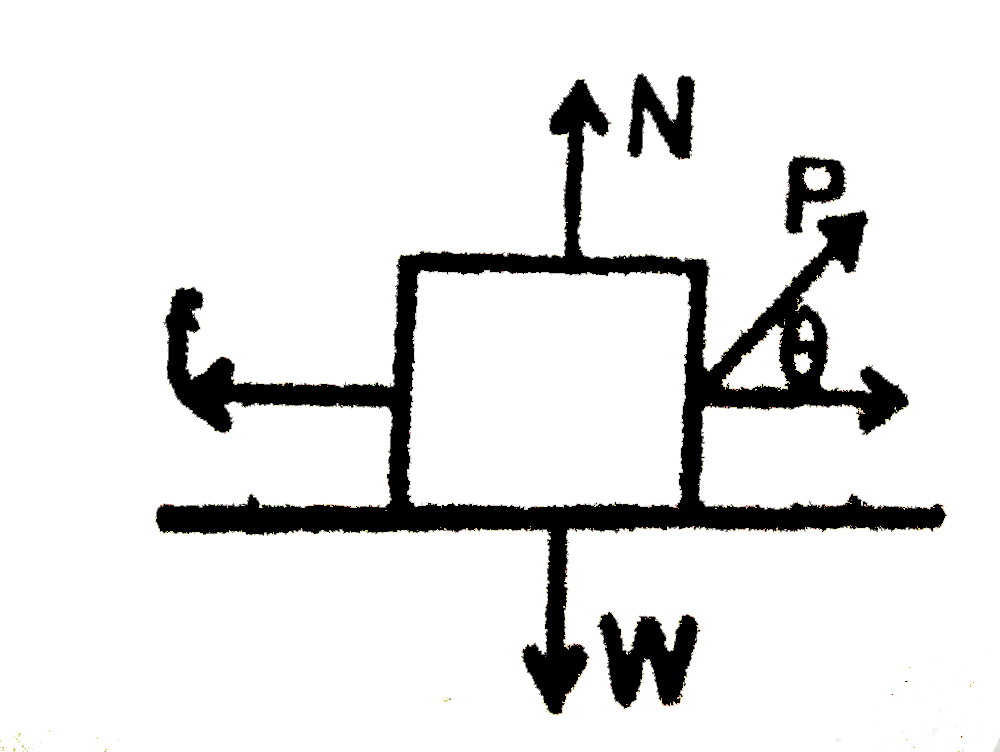
View SolutionA student pulls a wooden box along a rough horizontal floor( without the block loosing contact with the floor) at constant speed by means of a force P as shown to the right. (W is weights of block, N is normal reaction on the block, f is force of friction on the block). which of the following must be true?
View SolutionA box 'A' is lying on the horizontal floor the compartment of a train running along horizontal ralls from left to right. At time 't', it decelerates. Then the resultant contact force R by the floor on the box is given best by :
View SolutionA block `A` of mass `2 kg` rests on another block `B` of mass `8 kg` which rests on a horizontal floor. The coefficient of friction between `A` and `B` is `0.2` while that between `B` and floor is `0.5`.When a horizontal floor `F` of `25 N` is applied on the block `B` the force of friction between `A` and `B` is
View SolutionA weight w is to be moved from the bottom to the top of an inclined plane of inclination `theta` to the horizontal. If a smaller force is to be applied to drag it along the plane in comparison to lift it vertically up, the coefficient of friction should be such that.
View SolutionIn the arrangements shown in the figure there is friction only between the light string and the sharp spike at the point P. when the blocks are in motion, the tensions in the vertical and horizontal sections of the string are 4N and 3N respectively. The co-efficient of friction between the string and the spike is equal to
View SolutionStarting form rest, a body slides down a `45^(@)` inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionA uniform rope so lies on a table that part of it lays over. The rope begins to slide when the length of hanging part is 25% of entire length. The co-efficient of friction between rope and table is
View SolutionA body is projected up along the rough inclined plane from the bottom with some velocity. It travels up the incline and then returns back. If the time of ascent is `t_(a)` and time of descent is `t_(d)` then
View SolutionA chain of length L is placed on a horizontal surface as shown in figure At any instant x is the length of chain on rough surface and the remaining portion lies on smooth surface limitlly ` x= 0` A horizontal force p is applied to the chain (as shown in figure) in the duration from `x = 0 to x = L` For chain to move with constant speed
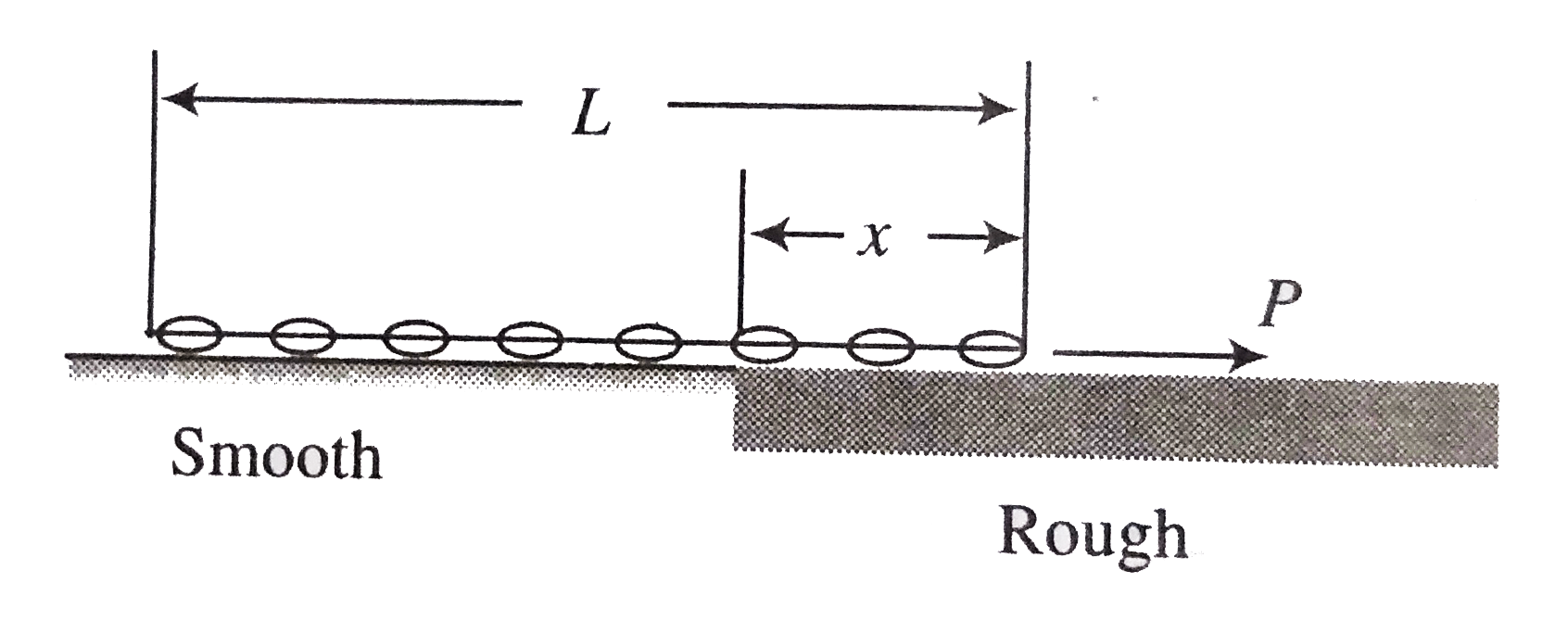
View Solution
With reference to the figure shown, if the coefficient of friction at the surfaces is 0.42, then the force required to pull out the 6.0 kg block with an acceleration of `1.50(m)/(s^2)` will be:
View SolutionA block of mass `15 kg` is resting on a rough inclined plane as shown in figure ,The block is tied by a horizontal string which has a tension `50 N` The coefficient of friction of contact is
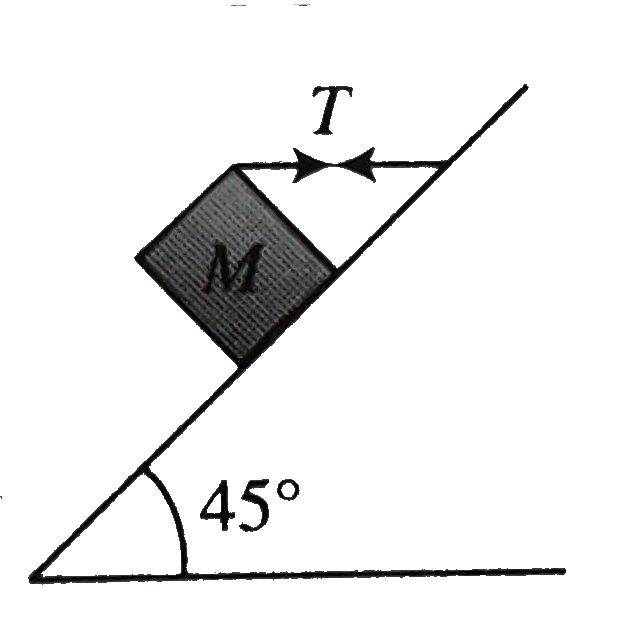
View SolutionWhat is the minimum stopping distance for a vehicle of mass `m` moving with speed `v` along a level road. If the coefficient of friction between the tyres and the road is `mu`.
View SolutionIn the shown arrangements if `f_(1), f_(2)` and T be the frictional forces on 2 kg block, 3 kg block & tension in the string respectively, then their values are

View SolutionA block is given velocity 10 m/s along the fixed inclined as shown in figure from the bottom of the inclined plane. Find the total distance travelled along the inclined plane. If the coefficient of friction is equal to 0.5
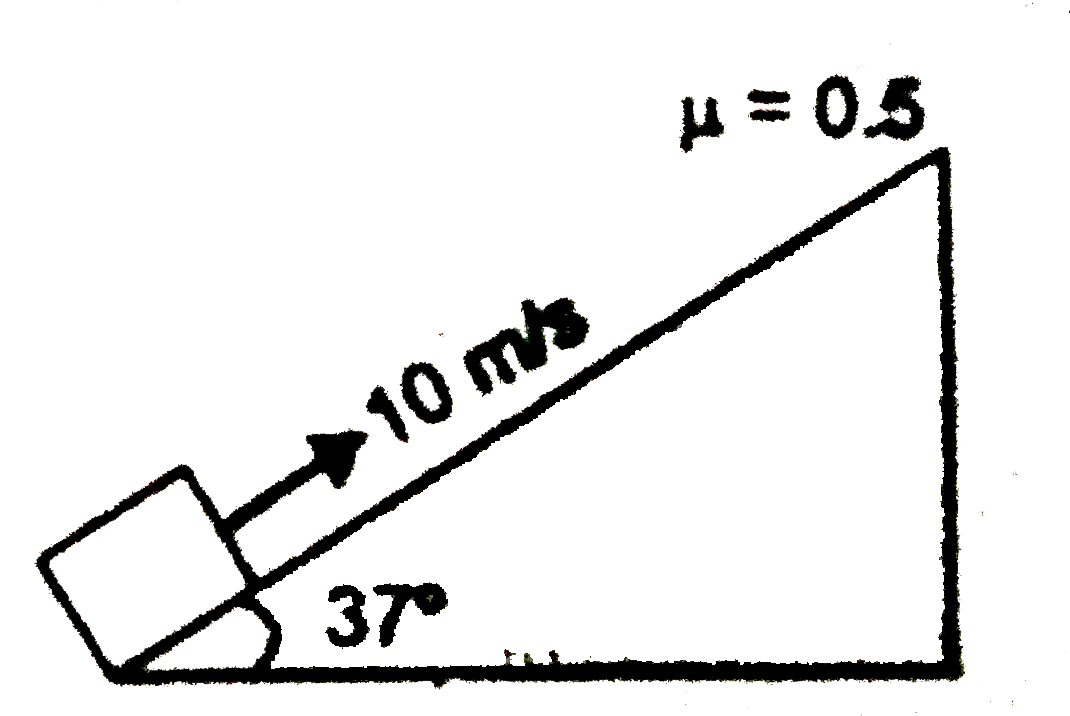
View SolutionCar is accelerating with acceleration `=20 m//s^(2)`. A box of mass m=10 kg that is placed inside the car, it is put in contact with the vertical wall of car as shown. The friction coefficient between the box and the wall `mu=0.6`
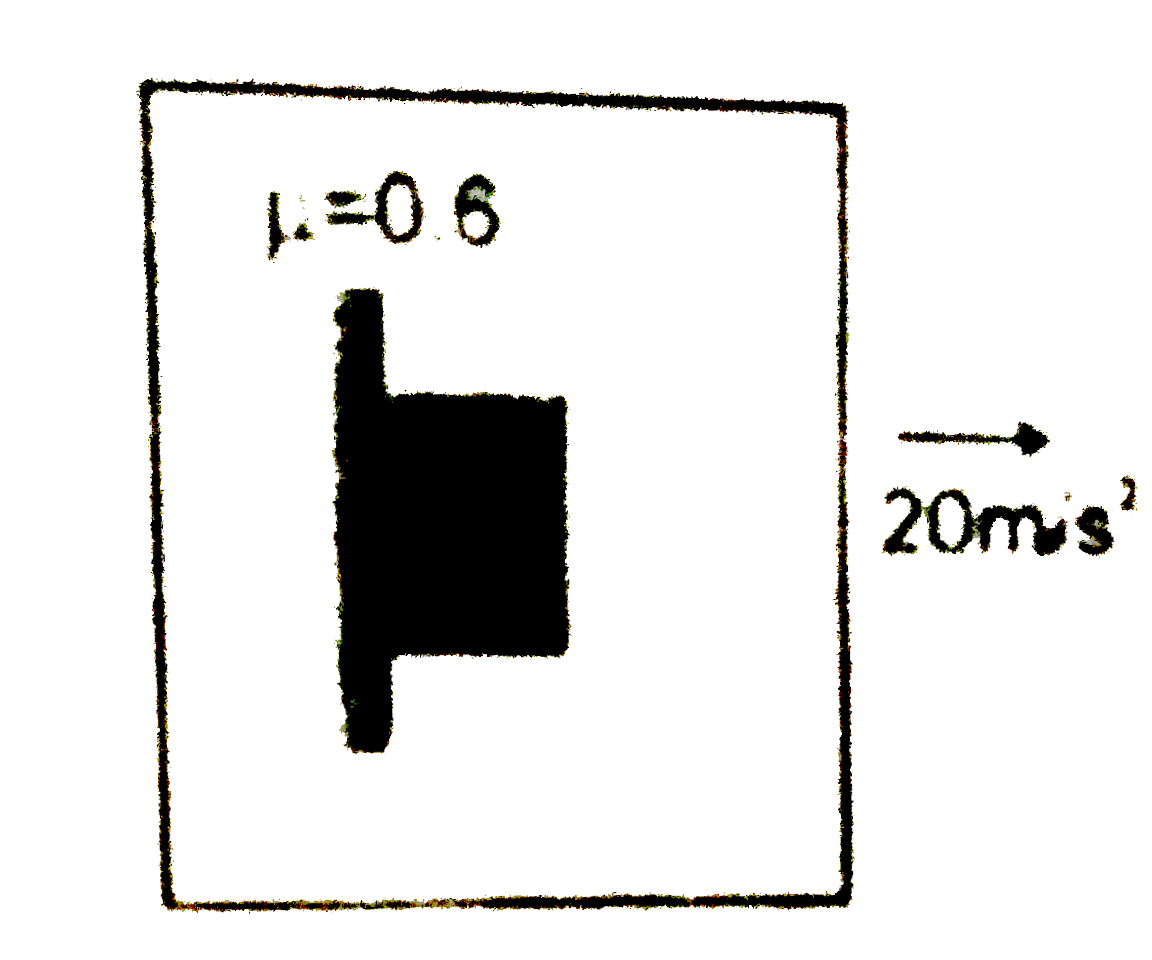
View SolutionA body of mass 10 kg lies on a rough horizontal surface. When a horizontal force of F newtons acts on it, it gets an acceleration of `5 m//s^(2)`. And when the horizontal force is doubled, it gets an acceleration of `18 m//s^(2)`. The coefficient of friction between the body and the horizontal surface is
View SolutionA block is placed on a rough floor and a horizontal force F is applied on it. The force of friction f by the floor on the block is measured for different values of F and a graph is plotted between them.
View Solution
Exercise questions and complete solutions for chapter NEWTONS LAWS OF MOTION AND FRICTION of RESONANCE ENGLISH of Class 11