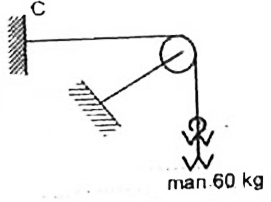
One end of massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum vertical force that the clamp can bear is 360 N. With what value of minimum safe acceleration ( in ms−2) can a man of 60 kg climp down the rops ?
10
5
8
4
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the man climbing down the rope and apply Newton's second law of motion.
1. Identify the Forces Acting on the Man:
- The weight of the man (W) acting downwards: W=mg
- The tension (T) in the rope acting upwards.
2. Write Down the Given Values:
- Mass of the man, m=60kg
- Maximum tension the clamp can bear, Tmax=360N
- Acceleration due to gravity, g=10m/s2
3. Calculate the Weight of the Man:
W=mg=60kg×10m/s2=600N
4. Apply Newton's Second Law:
- According to Newton's second law, the net force acting on the man is equal to the mass of the man multiplied by his acceleration:
W−T=ma
where a is the acceleration of the man downwards.
5. Substitute the Known Values:
- Rearranging the equation gives:
600N−T=60kg×a
- We know that the maximum tension T can be 360N:
600N−360N=60kg×a
6. Calculate the Net Force:
240N=60kg×a
7. Solve for Acceleration a:
a=240N60kg=4m/s2
Final Answer:
The minimum safe acceleration with which the man can climb down the rope is 4m/s2.
---
- The weight of the man (W) acting downwards: W=mg
- The tension (T) in the rope acting upwards.
- Mass of the man, m=60kg
- Maximum tension the clamp can bear, Tmax=360N
- Acceleration due to gravity, g=10m/s2
W=mg=60kg×10m/s2=600N
- According to Newton's second law, the net force acting on the man is equal to the mass of the man multiplied by his acceleration:
W−T=ma
where a is the acceleration of the man downwards.
- Rearranging the equation gives:
600N−T=60kg×a
- We know that the maximum tension T can be 360N:
600N−360N=60kg×a
240N=60kg×a
a=240N60kg=4m/s2
The minimum safe acceleration with which the man can climb down the rope is 4m/s2.
Topper's Solved these Questions
Similar Questions
One end of a massless rope, which passes over a massless and frictionless pulley P is tied to fixed hook C, while the other end is free. Maximum tension that the rope can bear is 960 N. With what value of max. safe acceleration (m/s2) can a man of 60 kg climb on the rope?
 View Solution
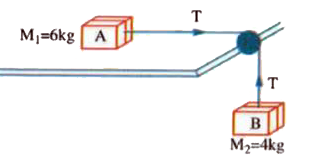
View SolutionA block A of mass 6kg is applied on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 4kg at the other end. Find the acceleration of the system and tension in the thread (given g=10ms−2)
 View Solution
View SolutionTwo masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
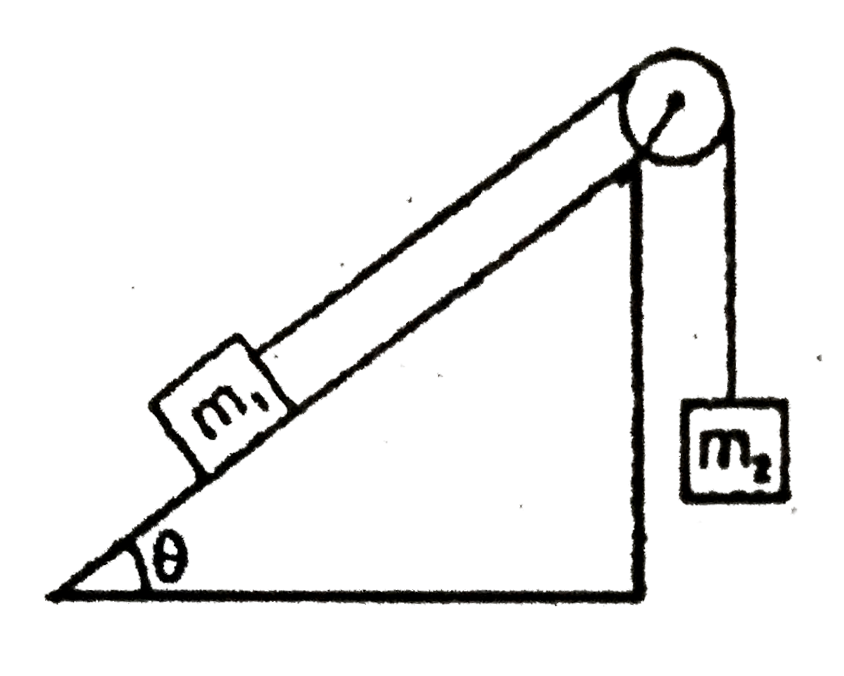
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?View SolutionTow men of masses m1andm2 hold on the opposite ends of a rope passing over a frictionless pulley. The men m1 climbs up the pore with an acceleration of 1.2m/s2 relative to the rope. The mann m2 climbs up the rope with an acceleration of 2m/s2 relative to the rope. Find the tension in the rope if m140kgandm2=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.
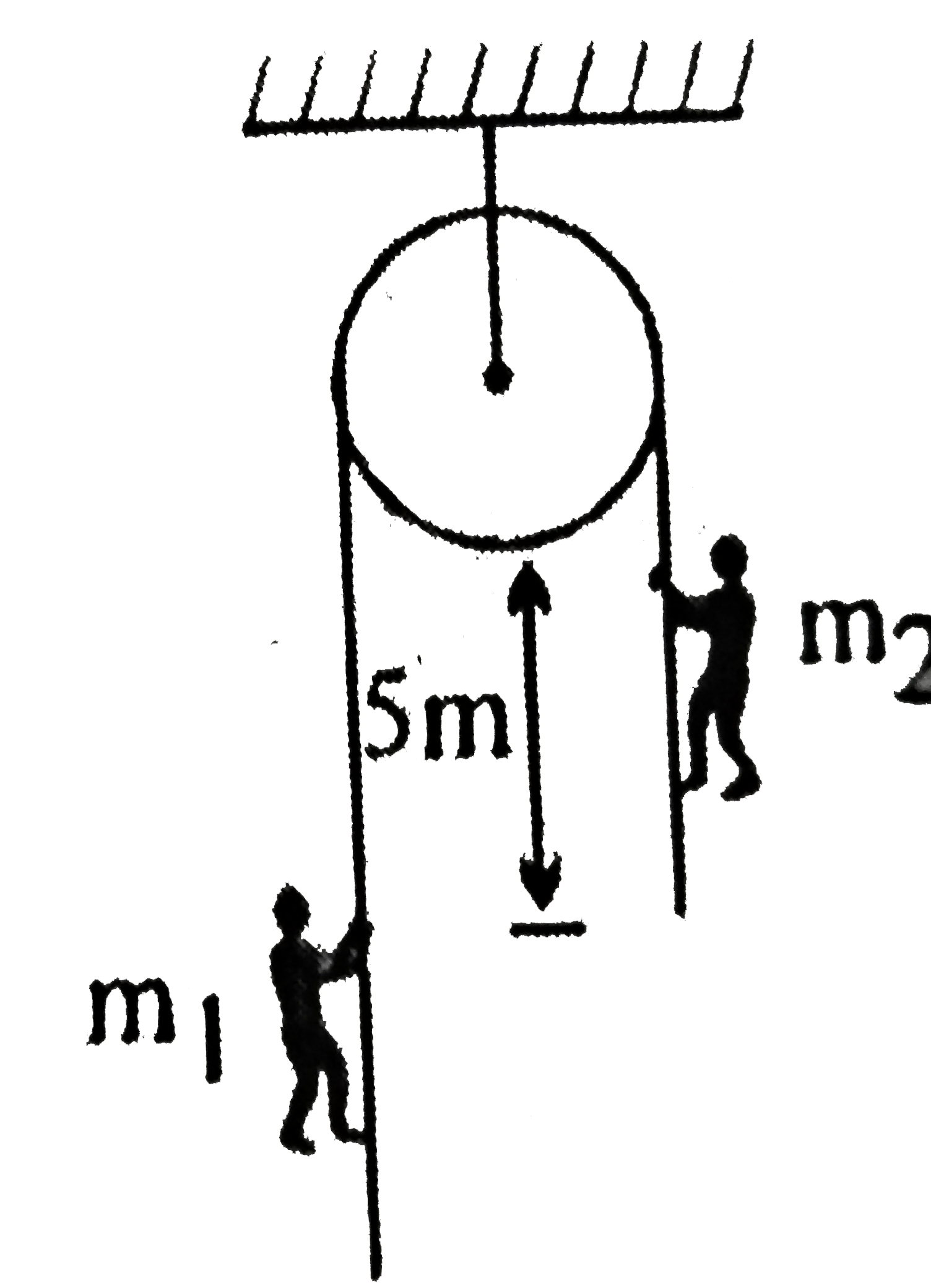 View Solution
View SolutionA 40 kg boy climbs a rope that passes over an ideal pulley. The other end of the rope is attached to a 60 kg weight placed on the ground. What is the maximum upward acceleration the boy can have without lifting the weight ? If he climbs the rope with upward acceleration 2 g, with what acceleration the weight will rise up ?
View SolutionBlock A of mass m/2 is connected to one end of light rope which passes over a pulley as shown in fig. A man of mass m climbs the other end of rope with a relative acceleration of g/6 with respect to rope. Find the acceleration of block A and tension in the rope.
 View Solution
View SolutionA block A of mass 8 kg is placed on a frictionless horizontal table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 2 kg at the other end. Find the acceleration of the system. Also find the tension in the thread. If the thread is cut into two and tied to the ends of a spring of forceconstant 1600N/m, find the amount of stretching of the spring. Neglect the mass of thread and of spring (g=9.8m/s2)
View Solution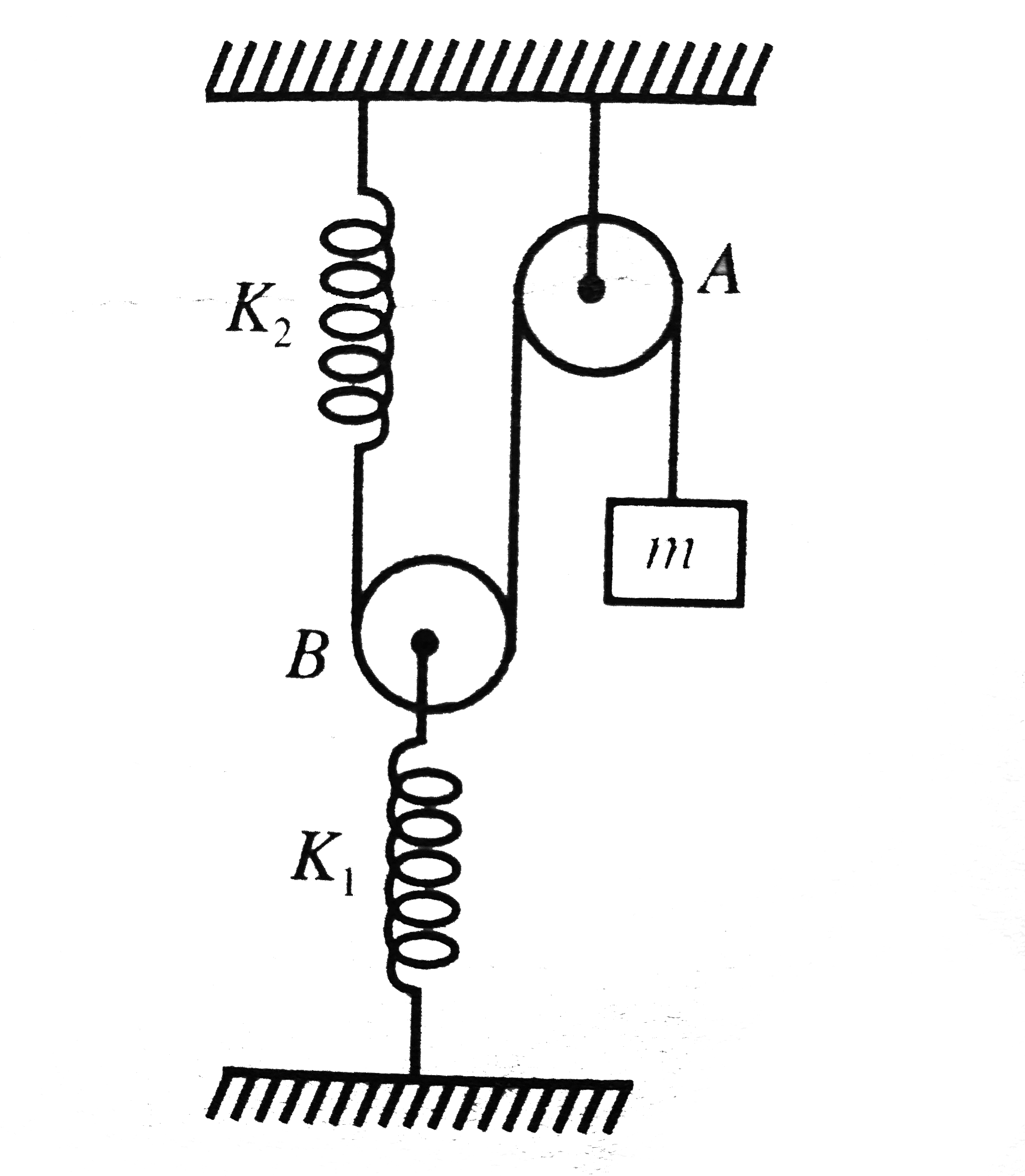
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)View SolutionThe pulley of the system shown in Fig is massless and frictionless and thread and thread is inextensible Then horizontal surface over which block C is smooth while for all the remaining surface is μ

Calculate minimum acceleration a with which the system should be moved to the right so that suspented block A(mass m ) and B (mass M and M>m)can remain stationary relative to CView SolutionTwo men of masses M and M+m start simultaneously from the ground and climb with uniform accelerations up from the free ends of a massless inextensible rope whick passes over a smooth pulley at a height h from the ground.
(a) Which man reaches the pulley first?
(b) If the mam who reaches first takes time t to reach the pulley, then find the distance of the second man from the pulley at this instant.View Solution

