Complete Solutions to Solved Example of chapter MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICS |
| SL ARORA | Solved Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
What is mechanics ? What are its various sub-branches ?
View SolutionDefine the terms rest and motion. Show that rest and motion are relative terms.
View SolutionCan a body exist in a state of absoulate rest or of absolute rest or of absolute motion ? Explain
View SolutionWhat is meant by a point object ? Give suitable examples.
View SolutionWhat do you mean by motion in one, two and three dimension ? Give examples of each type.
View SolutionDistinguish between distance and displacement.
View SolutionMention some important characteristics of diaplacement. Give illustrations to support these characteristics.
View SolutionDefine the term speed. Is it a scalar or vector quantity ? Give its unis and dimensions.
View SolutionDefine : uniform speed
View SolutionDefine : variable speed
View SolutionAVERAGE SPEED
View SolutionWhat do you mean by instantaneous speed?
View SolutionDefine the term velocity. Is it a scalar or vector quantity ? Give its units and dimensions.
View SolutionDefine : uniform velocity
View SolutionDefine : variable velocity
View SolutionDefine : average velocity
View SolutionINSTANTANEOUS VELOCITY
View SolutionWhen is the average speed of an object equal to the magnitude of its average velocity ? Give reason also.
View SolutionWhat is meant by uniform motion ?
View SolutionObtain the formulae for the position of an object moving with uniform velcity v at any time t in terms of its position at t = 0
View SolutionObtain the formulae for the position of an object moving with uniform velcity v at any time t' in the terms of its position at another time t.
View SolutionGive some important features of uniform motion.
View SolutionWhat is non-uniform motion ?
View SolutionIn Fig. 3.12 a particle moves along a circular parth of radius r. It starts from point A and moves anticlockwise. Find the distance travelled by the particle as it : moves from A to B

View SolutionIn Fig. 3.12 a particle moves along a circular parth of radius r. It starts from point A and moves anticlockwise. Find the distance travelled by the particle as it : moves from A to C
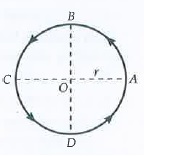
View SolutionIn Fig. 3.12 a particle moves along a circular parth of radius r. It starts from point A and moves anticlockwise. Find the distance travelled by the particle as it : moves A to D
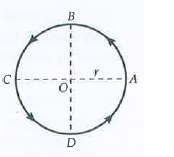
View SolutionA particle moves along a circle of radius `R. It starts from (A) and moves in antilockwise direction. Calculate the distance travelled by particle (a)one complete revolution. Also calcuate the magnituede of displacement in each case. Fig. 2 (a) .28.
View SolutionA body travels from `A to B` at `40 ms^(-1)`. And from `B to A` at 60 ms^(-1)`. Calculate the average speed and average velocity.
View SolutionOn a 60 km track, a train travels the first 30 km with a uniform speed of `30 kmh^(-1)`. How fast must the train travel the next 30 km so as to average `40 kmh^(-1)` for the entire trip ?
View SolutionA body covers one-third of its journey with speed 'u' , next third with speed 'v' and the last third with speed 'w'. Calculate the average speed of the body during the entire journey.
View SolutionA point traversed half the distance with a velocity `v_0`. The remaining part of the distance was covered with velocity `v_1` for half the time, and with velocity `v_2` for the other half of the time. Find the mean velocity of the point averaged over the whole time of motion.
View SolutionDefine the term acceleration. Is it a scalar or a vector quantity ? Give its units and dimensions.
View SolutionDefine the term uniform acceleration. Give one example of uniformly accelerated motion.
View SolutionExplain clearly (i) uniformacceleration (ii) variable acceleration (iii) Average acceleration (iv) instantaneous acceleration and show that instantaneous acceleration is the limition value of average acceleration.
View SolutionAVERAGE ACCELERATION
View SolutionINSTANTANEOUS ACCELERATION
View SolutionWhat are positive and negative accelerations ? Give examples.
View SolutionThe position of an object moving along x-axis is given by `x = a + bt^2` where `a=8.5 m, b=2.5 m s^-2 and t` is measured in seconds. What is its velocity at `t= 0 s and t = 2.0 s`. What is the average velocity between `t = 2.0 s and t = 4.0 s?`
View SolutionThe displacement (in metre) of a particle moving along x-axis is given by `x=18t +5t^(2). Calculate (i) the instantaneous velocity `t=2 s` (ii) average velocity between `t=2 s` to `t=3 s` (iii) instantaneous acceleration.
View SolutionThe displacement (in metre) of a particle moving along x-axis is given by `x=18t +5t^(2). Calculate (i) the instantaneous velocity `t=2 s` (ii) average velocity between `t=2 s` to `t=3 s` (iii) instantaneous acceleration.
View SolutionThe displacement (in metre) of a particle moving along x-axis is given by `x=18t +5t^(2). Calculate (i) the instantaneous velocity `t=2 s` (ii) average velocity between `t=2 s` to `t=3 s` (iii) instantaneous acceleration.
View SolutionThe displacement x of a particle varies with time t as
`x=4t^(2)-15t+25`
Find the position, velocity and acceleration of the particle at t=0. When will the velocity of the particle become zero? Can we call the motion of the particle as one with uniform acceleration ?
View SolutionThe velocity of a particle is given by the equation, `v = 2t^(2) + 5 cms^(-1) ` . Find
the change in velocity of the particle during the time interval between `t_(1) = 2s and t_(2) = 4s` .
View SolutionThe velocity of a particle is given by the equation, `v = 2t^(2) + 5 cms^(-1) ` . Find
the average acceleration during the time interval between`t_(1) = 2s and t_(2) = 4s` .
View SolutionThe velocity of a particle is given by the equation, `v = 2t^(2) + 5 cms^(-1) ` . Find
the instantaneous acceleration at `t_(2) = 4s`
View SolutionThe distance x of a particle moving in one dimensions, under the action of a constant force is related to time t by the equation, `t=sqrt(x)+3`, where x is in metres and t in seconds. Find the displacement of the particle when its velocity is zero.
View SolutionThe acceleration a in `ms^-2` of a particle is given by `a=3t^2+2t+2`, where t is the time. If the particle starts out with a velocity `v=2ms^-1` at `t=0`, then find the velocity at the end of `2s`.
View SolutionThe distance-time graph of the motion of an object moving with a contant speed is a straight line.
View SolutionDerive the equation of motion
`x=v_0t+1/2at^2` using appropriate graph.
View SolutionDerive the following equations of motion for an object moving with constant acceleration along a straight line : `v^(2) = v_0^(2) + 2a(x - x_0) = v_0^(2) + 2as`
View SolutionDerive the following equations of motion for an object moving with constant acceleration along a straight line : `s_nth = v_0 + a/2 (2n-1)`.
View SolutionDeduce the following equations for uniformly accelerated motion by using integration technique : v = u + at
View SolutionDeduce the following equations for uniformly accelerated motion by using integration technique : `s = ut + 1/2 at^(2)`
View SolutionDeduce the following relations analytically for a uniformly accelerated motion along a at. Iine, where terms have their usual meanings
` (i) v=u + at`
` (ii) s= ut = 1/2 at^2`
` (iii) v^2 =u^2 + 2 as`.
View SolutionDeduce the following equations for uniformly accelerated motion by using integration technique : `s_nth = u + a/2 (2n - 1)`
View SolutionA jet plane starts from rest with an acceleration of `3 ms^(-2)` and makes a run for 35 s before taking off. What is the minimum length of the runway and what is the velocity of the jet at take off ?
View SolutionAn electron travelling with a speed of `5xx10^(3) ms^(-1)` passes through an electric field with an acceleration of `10^(12)ms^(-2)`. (i) How long will it take for the electron to double its speed ?(ii) What will be the distance covered by the electron in this time?
View SolutionAn electron travelling with a speed of `5xx10^(3) ms^(-1)` passes through an electric field with an acceleration of `10^(12)ms^(-2)`. (i) How long will it take for the electron to double its speed ?(ii) What will be the distance covered by the electron in this time?
View SolutionA driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he ils driving a car at a speed of 54 km/h and the brakes cause a deceleration of `6.0 m/s^2`, find the distance travelled by the car after he sees the need to put the brakes on.
View SolutionOn a foggy day two drivers spot each other when they are just 80 meters apart. They are travelling at `27kmh^(-1)` and `60kmh^(-1)` , respectively. Both of them applied brakes retarding their cars at the rate of `5ms^(-1)` Determine whether they avert collision or not.
View SolutionA hunderd metre sprinter increases her speed from rest uniformly at the rate of `1ms^(-2)` upto three quarters of the total run and covers the last quarter with uniform speed. How much time does she take to cover the first half and the second half of the run?
View SolutionA motor car starts from rest and accelerates uniformly for 10 s to a velocity of `20 ms^(-1)`. It then runs at a constant speed and is finally brought to rest in 40 m with a constant acceleration. Total distance covered is 640 m. Find the value of acceleration, retardation and total tie taken.
View SolutionAn athlete runs a distance of 1500m in the following manner. (i) Starting from rest, he accelerates himself uniformly at `2ms^(-2)` till he covers a distance of 900m. (ii) He, then runs the remaining distance of 600m at the uniform speed developed. Calculate the time taken by the athlete to cover the two parts of the distance covered. Also find the time, when he is at the centre of the track.
View SolutionAn athlete runs a distance of 1500m in the following manner. (i) Starting from rest, he accelerates himself uniformly at `2ms^(-2)` till he covers a distance of 900m. (ii) He, then runs the remaining distance of 600m at the uniform speed developed. Calculate the time taken by the athlete to cover the two parts of the distance covered. Also find the time, when he is at the centre of the track.
View SolutionA man is l=9 m behind the door of a train when it starts moving with acceleration a=`2 m//s^2`.The man runs at full speed. How far does he have to run and after what time does he get into the train ? What is his full speed ?
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta,` to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car acceleration form rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta`, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA body covers 12m in 2nd second and 20m in 4th second. How much distance will it cover in 4 seconds after the 5th second ?
View SolutionA particle is moving in a straight line with constant acceleration. If x,y and z be the distances described by a particle during the pth, qth and rth second respectively, prove that (q-r)x+(r-p)y+(p-q)z=0
View SolutionTwo busses A and B are at positions 50m and 100m from the origin at time t=0. They start moving in the same direction simultaneously wi8th uniform velocities of `10ms^(-1)` and `5ms^(-1)` . Determine the time and position at which A overtakes B.
View SolutionAn object is moving along +ve x-axis with a uniform acceleration of `4ms^(-2)` . At time t=0 , x=5m and `v=3ms^(-1)` .
(a) What will be the velocity and position of the object at time t=2s?
What will be the velocity and position of the object when it has a velocity of `5ms^(-1)`?
View SolutionAn object is moving along +ve x-axis with a uniform acceleration of `4ms^(-2)` . At time t=0 , x=5m and `v=3ms^(-1)` .
(a) What will be the velocity and position of the object at time t=2s?
What will be the velocity and position of the object when it has a velocity of `5ms^(-1)`?
View SolutionFor a freely falling body
View SolutionA ball throuwn vertically upwards with a speed of `19.6ms^(-1)` from the top of a tower returns to the earth in 6s. Find the height of the tower.
View SolutionA ball is thrown vertically upwards with a velcotiy of `20 ms^(-1)` from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. `g=10 ms^(-2)`.
View SolutionA ball is thrown vertically upwards with a velocity of `20 ms^(-1)` from the top of a multistorey building. The height of the point from where the ball is thrown is 25 m from the ground. How long will it be before the ball hits the ground (Take, `g=10 ms^(-2)`) ?
View SolutionA ball is thrown vertically upwards with a velcotiy of `20 ms^(-1)` from the top of a multi-storey building. The height of the point fromwher the ball is thrown if 25m from the ground. (a) How high the ball will rise ? And (b) how long will it be before the ball hits the ground ? Take. `g=10 ms^(-2)`.
View SolutionA ball throuwn up is cautght by the thrower after 4s. How did it go and with what velocity was it thrown ? How far was it below the highest point 3s after it was thrown?
View SolutionA balloon is ascending at the rate of `9.8 m//s` and is 39.2 m above the ground when a package is dropped. (a) How long does the package take to reach the ground? (b) with what speed does it hit the ground ? `(g = 9.8 m//s^(2))`
View SolutionA food packet is released from a helicopter which is rising steadily at `2ms^(-1)` , After two second (i) What is the velocity of the packet ? (ii)How far is it below the helicopter?
Take `g=9.8ms^(-2)` .
View SolutionA food packet is released from a helicopter which is rising steadily at `2ms^(-1)` , After two second (i) What is the velocity of the packet ? (ii)How far is it below the helicopter?
Take `g=9.8ms^(-2)` .
View SolutionA parrachutist bails out from an aeropane and after dropping through a distance of `40 m` opens the parachute and decelerates at `2 ms^(-2)`. If he reaches the ground with a speed of `2 ms^(-1)`, how lowg he in the air ? At what height did he bail out from the plane ?
View SolutionTwo balls are thrown simultaneously, A vetically upwards with a speed of `20 ms^(-1)` from the ground, and B vetically downwards from height of 40 m with the same speed and along the same line of motion. At what points do the two balls collide? Take `g= 9.8 ms^(-2)`.
View SolutionA ball is dropped onto the floor from a height of 10 m. It rebounds to a height of 5 m. If the ball was in contact with the floor for `0.01 s`, what was its average acceleration during contact ? (Take `g=10 ms^(-2)`)
View SolutionA stone falls from a cliff and travels 24.5 m in the last second before it reaches the ground at the foot of the cliff. Find the height of the cliff.
View SolutionDraw the position-time graph of a stationary object.
View SolutionDraw the position-time graph for an object in uniform motion. Show that the slope of the position-time graph gives the velocity of the object.
View SolutionDraw the position-tie graph for uniformly accelerated motion. What does its slope give ?
View SolutionDraw the velocity-time graph for an object in uniform motion. Show that the area under the velocity-time graph gives the displacement of the object in the given time interval.
View SolutionDraw the velocity-time graph for uniformly accelerated motion. Show that slope of the velocity-time graph gives acceleration of the object.
View SolutionShow that the area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in that interval.
View SolutionDerive the following equations of motion for uniformly accelerated motion from velocity-time graph : v = u + at
View SolutionDerive the following equations of motion for uniformly accelerated motion from velocity-time graph : `s = ut + 1/2 at^(2)`
View SolutionDerive the following equations of motion for uniformly accelerated motion from velocity-time graph : `v^(2) - u^(2) = 2as`
View SolutionWhat is the nature of the distance-time graphs for uniform and non-uniform motion of an object ?
View SolutionWhat can you say about the motion of a body if :
(a) its displacement-time graph is a straight line ?
(b) its velocity-time graph is a straight line ?
View SolutionThe uniform motion in the following acceleration-time graph is
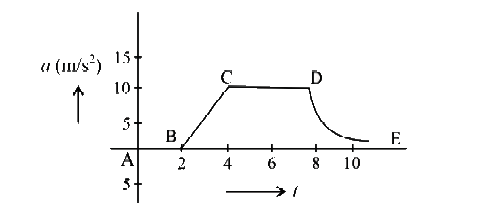
View SolutionFrom the top of a tower, a ball is droped to fall freely under gravity and at the same time, another bal is thrown up with a velocity of `50 ms^(-1)`. Plot the position-time graph for the motion of the two balls during the time interval t = 0 to t = 5s. Take `g = 10 ms^(-2)`
View SolutionA body starting from rest acclerates uniformly along a st. line , at the rate of `10 ms^(-2)` for 5 s. It moves for `2 s` with uniform velocoty of `50 ms^(-1)`. The it retards uniformly and comes to rest in 3 s`. Draw velocity-time graph of the and find the total distance travelled by body.
View SolutionA train moves from one station to another in two hours' time. Its speed-time graph during the motionis shown in Fig. 3.59 : calculate the distance covered during the time interval from 0.75 hour to 1 hour.
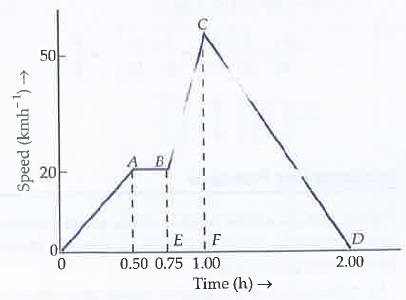
View Solution
Solved Example questions and complete solutions for chapter MECHANICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11