Complete Solutions to Exercise of chapter MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MECHANICS |
| SL ARORA | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A cyclist moving on a circular track of radius 100 m completes one revolution in 4 minutes What is his average speed ?
02:20View SolutionA cyclist moving on a circular track of radius 100 m completes one revolution in 4 minutes What is his average velocity in one full revolution ?
02:24View SolutionA body travels a distance `s_(1)` with vleocity `v_(1)` and distance `s_(2)` with velocity `v_(2)` in the with velocity `v_(2)` . Calculate the average velocity.
01:16View SolutionA car covers the first half of the distance between two places at a speed of `40 kmh^(-1)` and second half at `60 kmh^(-1)` Calculate the average speed of the car.
02:07View SolutionA train moves with a speed o f`30kmh^(-1)` in the first 15 minutes,with another speed of `40kmh^(-1)` the next 15 minutes,and then with a speed of `60 kmh^(-1)` in the last 30 minutes. Calculate the average speed of the train of train for this journey.
02:27View SolutionThe body travels a distance `s_(1) ` with velcity ` v_(1)` and `s_(2)` with velcity `v_(2)` in the same directin. Calculate the average velocity of the body .
01:59View SolutionA car along a starigth line for the first half time with speed `50 kmh^(-1)` and the second half time with speed `60kmh^(-1)`. Find the average speed of the car.
02:15View SolutionThe displacement x of a particle at time t along a straight line is given by `x = alpha - beta t+gamma t^(2)`. The acceleraion of the particle is
01:42View SolutionThe displacement x of a particle is dependent on time t according to the relation : `x = 3 - 5t + 2t^(2)`. If t is measured in seconds and s in metres, find its velocity at t = 2s.
02:17View SolutionThe displacement x of a particle is dependent on time t according to the relation : `x = 3 - 5t + 2t^(2)`. If t is measured in seconds and s in metres, find its acceleration at t = 4s.
01:54View SolutionThe displacement of a particle along the x-axis is given by `x=3+8t+7t^2`. Obtain its velocity and acceleration at `t=2s`.
01:50View SolutionThe distance traversed by a particle moving along a straight lne is given by `x = 180t+50t^(2)` metre. The acceleration of the particle is
01:06View SolutionThe distance traversed by a particle moving along a straight line is given by `x = 180 t + 50 t^(2)` metre. Find the velocity at the end of 4s.
01:29View SolutionThe distance traversed by a particle moving along a straight lne is given by `x = 180t+50t^(2)` metre. The acceleration of the particle is
01:06View SolutionA race car accelerates on a straight road from rest to a speed of `180 kmh^(-1)` in 25s. Assuming uniform acceleration of the car throughout, find the distance covered in this time.
02:31View SolutionA bullet travellling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
02:51View SolutionA car moving along a stainght highway with a speed of `72 kmh^(-1)` is brought to a stop within a distance of 100m. What is the retardation of the car and how long does it takes for the car to stop ?
03:00View Solutionon turning a corner a car driving at `36kmh^(-1)` finds a child on the road 55 m abead. He immediately applies brakes,so as to stop within 5 m of the child . Calculate the retardation produced and the time taken by the car to stop .
02:38View Solutionthe reaction time for an automobile drive os 0.6s if the automobile can be decelerated at `5 ms^(-2)` , calculate the total distance travelled in coming to stop fro, an intial velocity of `30kmh ^(-1)` after a singnal is observed.
05:05View SolutionA car starts from rest and accelerates uniformly for `10 s`to a velocity of `80 ms ^(-1)`. It then runs at a constant velocity and is finally brought to rest in `64 m` with a constant retardation. The total distance covered by the car is `584 m` Find the value of acceleration, retardation, and total time taken.
07:21View Solutiontwo tains one travelling at `72kmh^(-1)` and other at `90 kmh ^(-1)` are heading towards one another along a strauight level track. When they are 1.0km apart, both the drivers simultanously see the other 's train and apply brakes which restard each train at the rate of `1 .0ms^(-2)`.determine whether the trains would collide or not.
05:18View SolutionA scooter starts from rest have an acceleration of `1 ms^(-2)` while a car 150 m behind it starts from rest with an acceleration of `2ms^(-2)`. After how much time the car catches up with the scooter ?
02:11View SolutionA ball rolls down an inclined trck 2 m long in 4s. Find acceleration
01:59View SolutionA ball rolls down an inclined trck 2 m long in 4s. Find time taken to cover the second metre of the track.
03:46View SolutionA ball rolls down an inclined trck 2 m long in 4s. Find speed of the ball at the bottom of the track.
02:52View SolutionA bus starts from rest with constant acceleration of 5 `ms^–2`. At the same time a car travelling with a constant velocity of 50 `ms^–1` overtakes and passes the bus. (i) Find at what distance will the bus overtake the car ? (ii) How fast will the bus be travelling then ?
03:57View SolutionA bus starts from rest with a constant acceleration of `5 m//s^(2)` at the same time a car travelling with a constant velocity `50 m//s` over takes and passes the bus. How fast is the bus travelling when they are side by side?
04:31View SolutionA body starting from rest accelerates uniformly at the rate of `10cms^(-2)` and retaeds uniformly at the rate of `20cms^(-2)` . Find the least time in which it can complete the journey of 5km if the maximum velocity attained by the body is `72kmh^(-1)` .
06:40View SolutionA body covers `10 m` in the second second and `25 m` in fifth second of its motion. If the motion is uniformly accelerated, how far will it go in the the seventh second?
03:54View SolutionA body covers a distance of 4 m in `3^(rd)` second and 12m in `5^(th)` second. If the motion is uniformly accelerated. How far will it travel in the next 3 seconds?
04:59View SolutionAn object is moving with uniform acceleration. Its velocity after `4 s` is `20 ms^(-1)` and after `7 s` is `29 ms^(-1)` . Find the distance traveled by the object in 10th second.
03:40View SolutionA stone is thrown vertically upwards with a velocity of `4.9 ms^(-1)`. Calculate : the maximum height reached.
04:02View SolutionA stone is thrown vertically upwards with a velocity of `4.9 ms^(-1)`. Calculate : the time taken to reach the maximum height.
02:57View SolutionA stone is thrown vertically upwards with a velocity of `4.9 ms^(-1)`. Calculate : the velocity with which it returns to the ground.
03:01View SolutionA stone is thrown vertically upwards with a velocity of `4.9 ms^(-1)`. Calculate : the time taken to reach the ground.
04:28View SolutionA stone thrown upwards from the top of a tower 85 m high, reaches the ground in 5s. Find the greatest height above the ground.Take `g = 10 ms^(-2)`
04:10View SolutionA stone is thrown upwards from the top of tower 85 m high , reaches the ground in 5 s. find (i) the greatest height it reaches above the ground (ii) the velocity with which it reaches the ground and (iii) the time taken to reach the maximum height . Take g =` 10ms ^(-2)`?
05:35View SolutionA stone is thrown upwards from the top of tower 85 m high , reaches the ground in 5 s. find (i) the greatest height it reaches above the ground (ii) the velocity with which it reaches the ground and (iii) the time taken to reach the maximum height . Take g =` 10ms ^(-2)`?
05:35View Solutionfrom the top of multi-storeyed building ,39.2 m tall , a boy projects a stone vertically upward with an initial velocity of `9.8 ms^(-1)` such that it finally drops to the ground (i) when will the stone reach the ground? (ii) whn will it pass through the point of projection ? (iii) what will be its velocity before striking the ground ? take g =`10ms^(-2)`
05:29View Solutionfrom the top of multi-storeyed building ,39.2 m tall , a boy projects a stone vertically upward with an initial velocity of `9.8 ms^(-1)` such that it finally drops to the ground (i) when will the stone reach the ground? (ii) whn will it pass through the point of projection ? (iii) what will be its velocity before striking the ground ? take g =`10ms^(-2)`
05:29View Solutionfrom the top of multi-storeyed building ,39.2 m tall , a boy projects a stone vertically upward with an initial velocity of `9.8 ms^(-1)` such that it finally drops to the ground (i) when will the stone reach the ground? (ii) whn will it pass through the point of projection ? (iii) what will be its velocity before striking the ground ? take g =`10ms^(-2)`
05:29View SolutionA rocket is fired vertically up from the ground with a resultant vertical acceleration of `10 m//s^2.` The fuel is finished in 1 min and it continues to move up. (a) What is the maximum height reached? (b) Afte2r how much time from then will the maximum height be reached?(Take `g= 10 m//s^2`)
07:16View SolutionA balloon is ascending at the rate of `14 ms^(-1)` at a height of 98 m above the ground when the food packet is dropped from the balloon. After how much time and with what velocity does it reach the ground ? Take `g = 9.8 ms^(-2)`
04:15View SolutionA stone is dropped from a balloon rising upwards with a velocity of `16 ms^(-1)`. The stone reaches the ground in 4 s. Calculate the height of the balloon when the stone was dropped.
03:03View SolutionForm the top of a tower `100 m` in height a ball is dropped and at the same time another ball is projected vertically upwards from the ground with a velcoity of `25 ms^(-1)`. Find when and where the two balls will meet.
04:55View SolutionAn object is dropped from rest at a height of `150 m` and simultanously another object is dropped from rest at a height `100m`. What is the difference in their height after `2 s` if both the objects drop with same acceleration ? How does the difference in height vary with time ?
02:49View SolutionA body is dropped from rest at a height of `150 m` and simultanceously, another body is dropped from rest from a point `100 m` above the ground. What is the difference between heights after theymave fallen for (i) `3s (ii) 5s`. Consider that the body on reaching ground remains there and acceleration due to gravity be `10 m//s^(2)`.
08:16View SolutionA body falling freely under gravity passes two points 30 m apart in 1 s. From what point above the upper point it began to fall? (Take g = `9.8 m s^(-2)`).
03:46View SolutionFour marbles are dropped from the top of a tower one after the other with an interval of one second. The first one reaches the ground after 4 seconds . When the first one reaches the ground the distance between the first and second, the second and third and the third and forth will be respectively
04:43View SolutionFigure 3.64 shows the position-time graphs of three car A, B and C. On the basis of the graphs, answer the following questions : Which car has the highest speed and which the lowest ?
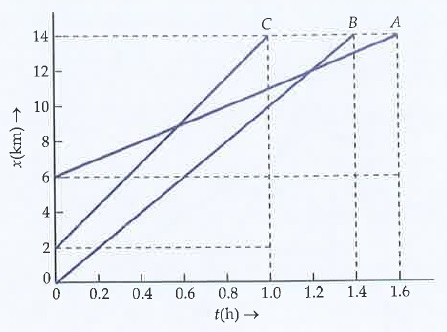 02:41View Solution
02:41View SolutionFigure 3.64 shows the position-time graphs of three car A, B and C. On the basis of the graphs, answer the following questions : Are the three cars ever at the same point on the road ?
 01:57View Solution
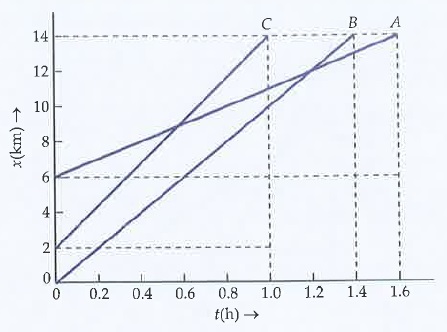
01:57View SolutionFigure 3.64 shows the position-time graphs of three car A, B and C. On the basis of the graphs, answer the following questions : When A passes C, where is B ?
 01:43View Solution
01:43View SolutionFigure 3.64 shows the position-time graphs of three car A, B and C. On the basis of the graphs, answer the following questions : How far did car A travel between the time it passed cars B and C ?
 02:30View Solution
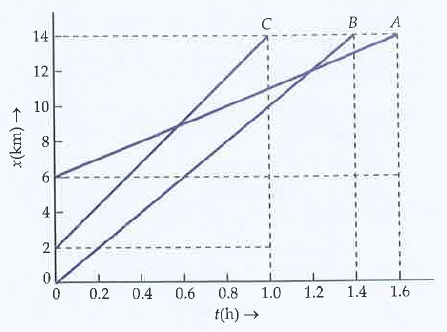
02:30View SolutionFigure shows the position-time graphs of three car A, B and C. On the basis of the graphs, answer the following questions : What is the relative velocity of car C with respect to car A ?
 06:39View Solution
06:39View SolutionFigure shows the position-time graphs of three car A, B and C. On the basis of the graphs, answer the following questions : What is the relative velocity of car B with respect to car C ?
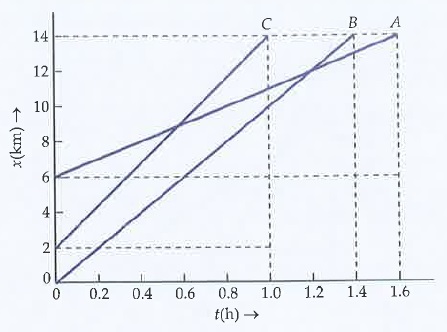 05:37View Solution
05:37View SolutionAn insect crawling up awall crawls 5 cm upwards in the first minute but then slides 3 cm downwardsin the next minute. It again crawls up 5 cm upwards in the third minute but again slides 3 cm downwards in the fourth minute. How long will the insect take to reach a crevice in the wall at a height of 24 cm from its starting point ? How does the position-time graph of the insect look like ?
11:17View Solutiona driver of a car travelling at `52 km//h` applies the brakes and acceleration uniformly in the opposite direction. The car stops in `5 s`. Another driver going at `34 km//h` in another car applies his brakes slowly and stops in `10 s`. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied ?
05:50View SolutionA motor car, starting from rest, moves with uniform acceleration and attains a velocity of `8 ms^(-1)` in 8 s. It then moves with uniform velocity and finally brought to rest in 32 m under unifrom retardation. The total distance covered by the car is 464 m. Find the acceleration.
01:55View SolutionA motor car, starting from rest, moves with uniform acceleration and attains a velocity of `8 ms^(-1)` in 8 s. It then moves with uniform velocity and finally brought to rest in 32 m under unifrom retardation. The total distance covered by the car is 464 m. Find the retardation
03:16View SolutionA motor car, starting from rest, moves with uniform acceleration and attains a velocity of `8 ms^(-1)` in 8 s. It then moves with uniform velocity and finally brought to rest in 32 m under unifrom retardation. The total distance covered by the car is 464 m. Find the total time taken.
05:25View SolutionStarting from rest a car accelerates unifromly with `3 ms^(-2)` for 5 s and then moves with uniform velocity. Drwa the distance-time graph of the motion of the car upto t = 7s.
04:10View SolutionThe velocity-time graph of an object moving along a straight line is as shown in Fig. 3.37. Find the net distance covered by the object in time interval between t=0 to t=10s. Also find the displacement in time 0 to 10 s.
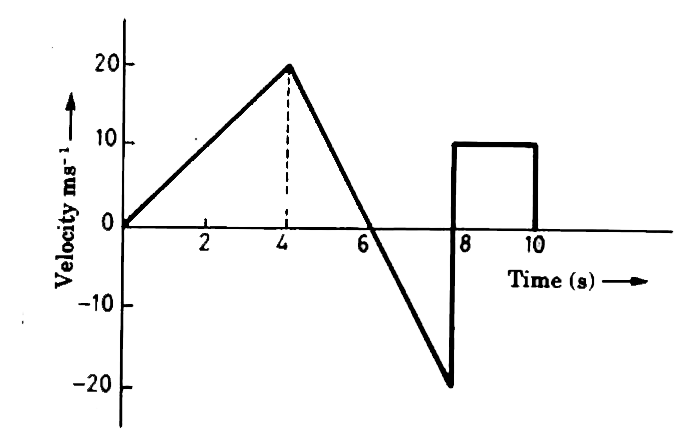 01:47View Solution
01:47View SolutionAs soon as a car just starts from rest in a certain direction, a scooter moving with a uniform speed overtakes the car. Their velocity-time graphs are shown in Fig. Calculate the difference between the distances travelled by the car and the scooter in 15 s.
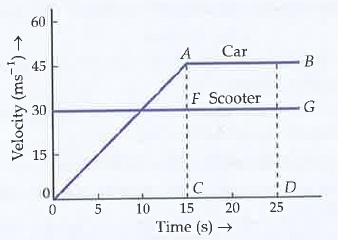 02:55View Solution
02:55View SolutionAs soon as a car just starts from rest in a certain direction, a scooter moving with a uniform speed overtakes the car. Their velocity-time graphs are shown in Fig. 3.66. Calculate the time when the car will catch up the scooter.
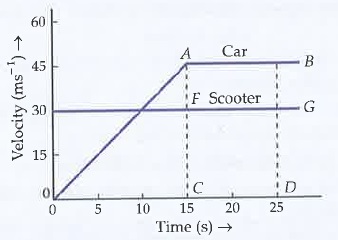 06:31View Solution
06:31View SolutionThe velocity (u)-time (t) graph of an object moving along a straight line is as shown is Fig. 2 (b) . 30. Calculate the distance covered by object between ` (i) t =0 to t=5 s` (ii) ` t=0 to t=10 s`.
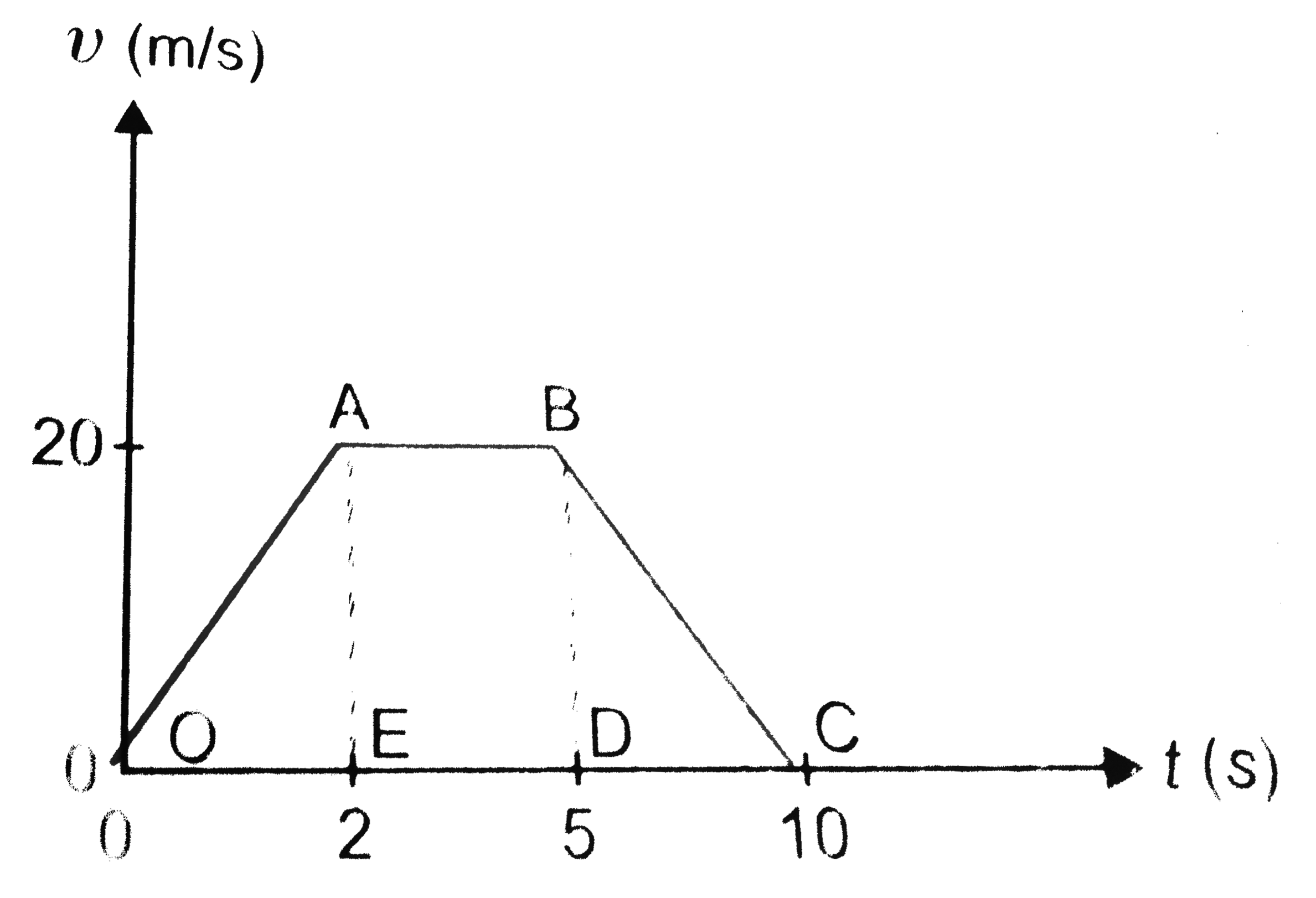 .02:32View Solution
.02:32View SolutionThe velocity (u)-time (t) graph of an object moving along a straight line is as shown is Fig. 2 (b) . 30. Calculate the distance covered by object between ` (i) t =0 to t=5 s` (ii) ` t=0 to t=10 s`.
 .02:32View Solution
.02:32View SolutionA jet airplane travelling at the speed of `450 kmh ^(-1)`ejects the burnt gases at the speed of `1200 kmh^(-1)` relative to the jet airplane. Find the speed of the brunt gases w.r.t a stationay observer on earth .
02:26View Solutiontwo car A and B are moving with velocities of `60 kmh^(-1) and 45 kmh^(-1)` respectively. Calculate the relative velocity of A w.r.t B if (i) both cars are travelling eastwards and (ii)car A is travelling eastwards and car B is travelling westwards.
02:06View Solutiontwo car A and B are moving with velocities of `60 kmh^(-1) and 45 kmh^(-1)` respectively. Calculate the relative velocity of A w.r.t B if (i) both cars are travelling eastwards and (ii)car A is travelling eastwards and car B is travelling westwards.
02:06View Solutionan open car is moving on a road with a speed of `100 kmh ^(-1)` . A man sitting in the car fires a bullet from the gun in the oppositve direction. If the spedd of the bullet is `250kmh ^(-1)` relative to the car.then find its (bullt 's ) speed with respect to an observe on the ground.
02:24View SolutionA car A is moving with is speed of `60kmh^(-1)` an car B is moving with a speed of `75 kmh^(-1)` ,along parallel strainght paths , starting paths starting from the same point. What is the position of car A w.r.t B after 20 mintues ?
02:01View Solutiontwo buses start simultaneoulsly towards each othehr from towns A and B which are 480 km apart. The first bus taken 8 hours to travel form A to B while the second bus takes 12 hours to travel from B to A. determine when and where the buses will meet.
03:01View SolutionTwo trains, each of length ` 100 m`, are running on parallel tracks. One overtakes the other in `20 second ` and one crosses the other in `10 second`. Calculate the velocities of two trains.
02:58View SolutionA man swins in a river with and against water at the rate of `15 kmh ^(-1) and 5 kmh^(-1)` . Find the man's speed in still water and the speed of the river.
05:48View SolutionA motor boat covers the distance between the two spost on the tiver in `9 h and 13 h` down stream and upstream respectively. Find the time required by the boat to cover this distance in still water.
08:00View SolutionA car A is travelling on a straight level road with a uniform speed of 60 km/h. It is followed by another car B which in moving with a speed of 70 km/h. When the distance between then is 2.5km, the car B is given a deceleration of `20(km)/(h^2)`. After how much time will B catch up with A
02:03View SolutionA particle is constrained to move on a straight line path. It returns to the starting point after 10 sec . The total distance covered by the particle during this time is 30 m . Which of the following statements about the motion of the particle is false
02:05View SolutionA car travels the first half of a distance between two places at a speed of `30 km// hr` and the second half of the distance at `50 km//hr` . The average speed of the car for the whole journey is
02:42View SolutionA car travels from A to B at a speed of `20 km//hr` and returns at a speed of `30 km//hr`. The average speed of the car for the whole journey is
02:06View SolutionIf the first one - third of q journey is travelled at 20 km `h^(-1)` , Next one - third at `40 km h^(-1)` And the last one third at `60 km h^(-1)` then the average speed for the whole journey will be
04:51View SolutionA person travelling on a straight line moves with a uniform velocity `v_1` for some time and with uniform velocity `v_2` for the next equal time. The average velocity v is given by
01:55View SolutionA 100 m long train is moving with a uniform velocity of `45 km//hr`. The time taken by the train to cross a bridge of length 1 km is
02:22View SolutionYou drive a car at a speed of `70 km//h` in a straight road for 8.4 km, and then the car runs out of petrol. You walk for 30 min to reach a petrol pump at a distance of 2 km. The average velocity from the beginning of your drive till you reach the petrol pump is
05:03View SolutionA car moving with a speed of 25 `ms^(-1) ` takes a U-turn in 5 seconds, without changing its speed. The average acceleration during these 5 seconds is
03:24View SolutionA particle moves along the x-axis with a position given by the equation x(t) = 5 + 3t, where x is in metres, and t is in seconds. The positive directions east. Which of the following statements about the particle is false ?
03:10View SolutionThe motion of a particle is described by the equation at `u = at`.The distance travelled by the particle in the first 4 seconds
01:55View SolutionThe acceleration a of a particle starting from rest varies with time according to relation, `a=alphat+beta`. Find the velocity of the particle at time instant t.
Strategy : `a=(dv)/(dt)`01:39View SolutionGiven a = 2t + 5`. Calculate the velocity of the body after 10 sec if it starts from rest.
01:59View SolutionWith the usual notations the following equation `S_(t)=u+1/2a(2t-1)` is
02:26View SolutionWhat is the relation between displacement, time and acceleration in case of a body having uniform acceleration
01:23View SolutionA body sliding down on a smooth inclined plane slides down `1//4th` distane in 2s. I will slide down the complete plane in
01:28View SolutionA particle moving in one dimension with a constant acceleration of `2 m/s^(2)` is observed to cover a distance of 5 m during a particular interval of 1 s. Thedistance covered by the particle in the next 1 s interval (in metre) is
02:42View SolutionA particle starts from rest, accelerates at `2(m)/(s^2)` for 10 s and then goes for constant speed for 30 s and then decelerates at `4(m)/(s^2)`. Till it stops. What is the distance travelled by it?
02:51View SolutionThe velocity of a particle at an instant is `10 m s^(-1)`. After 3 s its velocity will becomes `16 m s^(-1)`. The velocity at 2 s, before the given instant will be
02:33View SolutionA particle starts from rest with uniform acceleration `a`. Its velocity after 'n' second is 'v'. The displacement of the body in the last two second is
03:32View SolutionA car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate `beta` to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
05:53View SolutionThe velocity with which a body stricks the ground is always equal to the velocity with which it was projected upwards.' is the statement true ? On what principle is ist based ?
03:04View SolutionIf a ball is thrown vertically upwards with a velocity of `40m//s`, then velocity of the ball after `2s` will be `(g = 10m//s^(2))`
01:23View SolutionA stone released with zero velocity from the top of a water, reaches the ground in 4s. The height of the tower is `(g = 10 m//s^(2))`
01:27View SolutionA stone is thrown vertically up from the ground. It reaches a maximum height of 50 m in 10 sec. After what time it will reach the ground from maximum height position ?
06:39View Solution
Exercise questions and complete solutions for chapter MECHANICS of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11
