Complete Solutions to Example Solution of chapter PROJECTILE MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROJECTILE MOTION |
| SL ARORA | Example Solution |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
A passenger arriving in a new town wishes to go from the station to a hotel located ` 10 km` away on a straight road from the station. A dishonest cabman takes him along a circuitous path ` 23 km` long and reaches the hotel in ` 28` minutes . What is (a) the average speed of the taxi, (b) the magnitude of average velocity ? Are the two equal ?
View SolutionA cyclist travels from centre O of a circular park of radius 1 km and reaches point P. After cycling along `1//4` th of the circumference along PQ, he returns to the centre of the park along QO. If the total time taken is 10 minutes, calculate (i) net displacement (ii) average velocity and (ii) average speed of the cyclist.
View SolutionOn an open ground , a motorist follows a track that turns to his left by an angle of ` 60^@` after every ` 500 m`. Starting from a given turn , specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with total path length covered by the motorist in each case.
View SolutionAn aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10 s apart is `30^(@)` , what is the speed of the aircraft ?
View SolutionA projectile is fired horizontally with a velocity of `98 ms^(-1)` from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionA body is thrown horizontally from the top of a tower and strikes the ground after three seconds at an angle of `45^@` with the horizontal. Find the height of the tower and the speed with which the body was projected. (Take ` g = 9.8 m//s^2`)
View SolutionA bomb is dropped from an aeroplane when it is directly above a target at a height of 1000m. The aeroplane is moving horizontally with a speed of `500 kmh^(-1)`. By how much distance will the bomb miss the target ?
View SolutionTwo tall buildings face each other and are at a distance of 180 m from each other. With what velocity must a ball be thrown horizontally from a window 55 m above the ground in one building, so that it enters a window 10.9 m above the ground in the second building ?
View SolutionA body is projected horizontally from the top of a cliff with a velocity of `9.8ms^(-1)`. What time elapes before horizontal and vertical velocities become equal ? Take `g=9.8 ms^(-2)`.
View SolutionTwo paper screens `A` and `B` are separated by a distance of `100m`. A bullet pierces `A` and `B`. The hole in `B` is `10 cm` below the hole in `A`. If the bullet is travelling horizontally at the time of hitting the screen `A`, calculate the velocity of the bullet when it hits the screen `A`. Neglect resistance of paper and air.
View SolutionA marksman wishes to hit a target just in the same level as the line of sight. How high from the target he should aim, if the distance of the target is 1600 m and the muzzle velocity of the gun is `800 ms^(-1)` ? Take `g = 9.8 ms^(-2)`.
View SolutionA body is projected with a velocity of `30 ms^(-1)` at an angle of `30^(@)` with the vertical. Find the maximum height, time of flight and the horizontal range.
View SolutionA cricketer can throw a ball to a maximum horizontal distance of 100 m. How high above the ground can the cricketer throw the same ball ?
View SolutionThe ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of `40 ms^(-1)` can go without hitting the ceiling of the hall ?
View SolutionA bullet fired at an angle of `30^(@)` with the horizontal hits the ground 3 km away. By adjusting the angle of projection, can one hope to hit a target 5 km away ? Assume the muzzle speed to be fixed and neglect air resistance.
View SolutionA projectile has a range of 50 m and reaches a maximum height of 10 m. Calculate the angle at which the projectile is fired.
View SolutionFind the angle of projection for which the horizontal range and the maximum height are equal.
View SolutionProve that the maximum horizontal range is four times the maximum height attained by the projectile, when fired at an inclination so as to have maximum horizontal range.
View SolutionShow that a given gun will shoot three times as high when elevated at an angle of `60^(@)` as when fired at angle of `30^(@)` but will carry the same distance on a horizontal plane.
View SolutionA ball is thrown at angle `theta` and another ball is thrown at an angle `(90^(@)-theta)` with the horizontal direction from the same point with velocity `39.2 ms^(-1)`. The second ball reaches 50 m higher than the first ball. Find their individual heights. Take `g = 9.8 ms^(-2)`.
View SolutionIf `R` is the horizontal range for `theta` inclination and `h` is the maximum height reached by the projectile, Then maximum range is
View SolutionFor given value of u, there are two angles of projection for which the horizontal range is the same. Show that the sum of the maximum heights for these two angles is independent of the angle of projection.
View SolutionShow that there are two values of time for which is projectile is at the same height. Also show that the sum of these two times is equal to the time of flight.
View SolutionA ball is kicked at an angle of `30^(@)` with the vertical. If the horizontal component of its velocity is `19.6 ms^(-1)`, find the maximum height and horizontal range.
View SolutionA fighter plane flying horizontally at an altitude of ` 1.5 km` with speed ` 720 kmh^(-1)` passes directly over head an anticraft gun.
At what angle from the vertical should the gun be fired from the shell with muzzle speed ` 600 ms^(-1)` to hit plane.
At what minimum altitude should the pilot fly the plane to avoid being hit ? ( Take g= 10 `ms^(-2)`).
View SolutionAt what angle should a body be projected with a velocity `24 ms^(-1)`. Just to pass over the obstacle 16 m high at a horizontal distance of 32 m ? Take `g = 10 ms^(-2)`.
View SolutionA target is fixed on the top of a pole 13 metre high. A person standing at a distance of 50 metre form the pole is capable of projecting a stone with a velocity `10 sqrt(g) ms^(-1)`. If he wants to strike the target in shortest possible time, at what angle should he project the stone ?
View SolutionTwo persons simultaneously aim and fire their guns at a bird sitting on a tree. The first person fires his shot with a speed of `100 m//s` at an angle of projection of `30^(@)`. The second person is ahead of the first by a distance of `50 m` and fire his shot with a speed of `80 m//s`. how must he aim his gun so that both the shots hit the bird simultaneously. Calculate the distance of the foot of the tree from two persons and the height of the tree. With what velocities and when do the two shots hit the bird.
View SolutionWhat is the angular velocity of a second hand and minute hand of a clock ?
View SolutionCalculate the angular speed of flywheel making 420 revolutions per minute.
View SolutionA circular wheel of 0.50 m radius is moving with a speed of `10 ms^(-1)`. Find the angular speed.
View SolutionA stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 seconds, what is the magnitude and direction of acceleration of the stone ?
View SolutionAn aircraft executes a horizontal loop of radius 1 km with a steady speed of `900 km h^(-1)`. Compare its centripetal acceleration with the acceleration due to gravity.
View SolutionAn insect trapped in a circular groove of radius 12 cm moves along the groove steadily and completes 7 revolutions in 100 s. (i) What is the angular speed and the linear speed of the motion ? (ii) Is the acceleration vector a constant vector ? What is its magnitude ?
View SolutionThe radius of the earth's orbit around the sun is `1.5 xx 10^(11)m`. Calculate the angular and linear velocity of the earth. Through how much angle does the earth revolve in 2 days?
View SolutionA cyclist is riding with a speed of `27 km h^(-1)`. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate `0.5 ms^(-2)`. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn ?
View SolutionA particle moves in a circle of radius 4.0 cm clockwise at constant speed of `2 ms^(-1)`. If `hat(x)` and `hat(y)` are unit acceleration vectors along X-axis and Y-axis respectively (in `cms^(-2)`), find the acceleration of the particle at the instant half way between P and Q. Refer to Fig.5.14 (a).
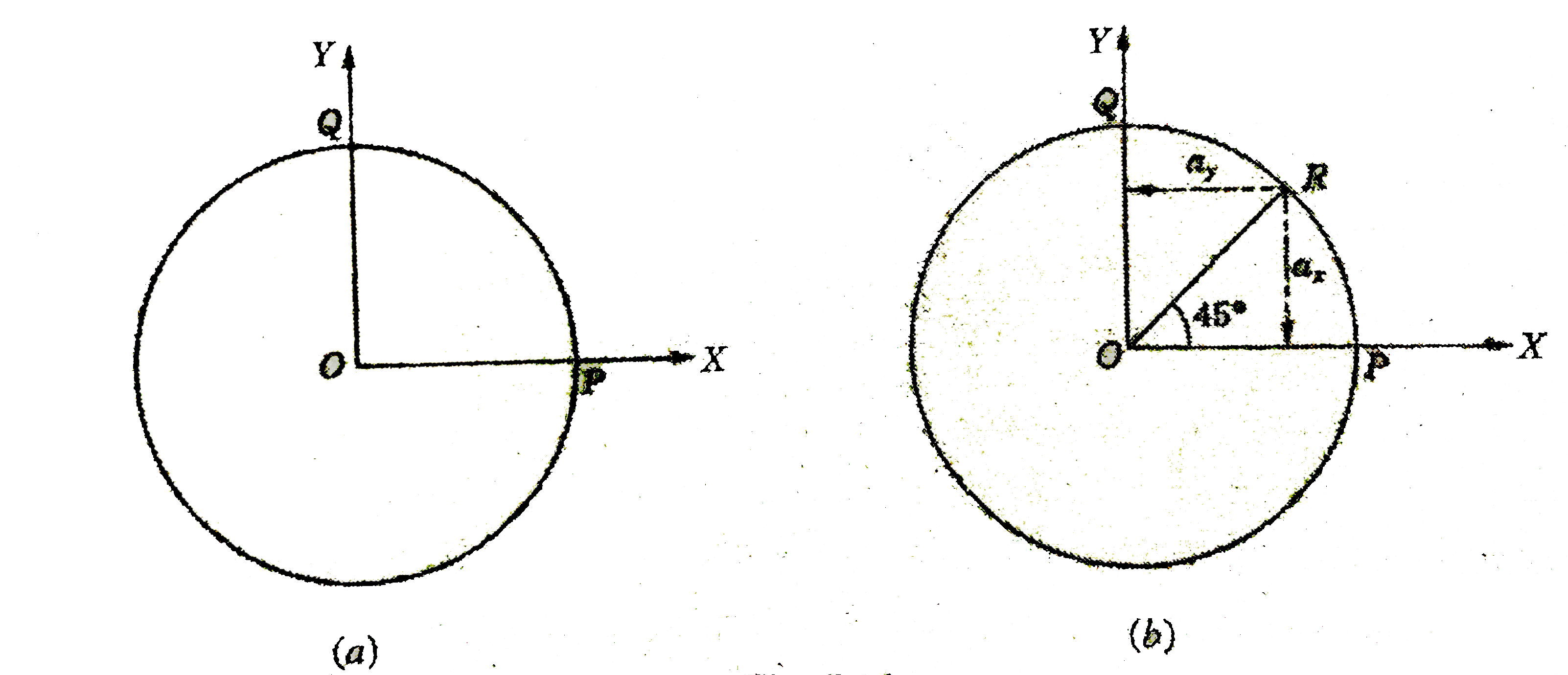
View Solution
Example Solution questions and complete solutions for chapter PROJECTILE MOTION of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11