Complete Solutions to Problen Solution of chapter PROJECTILE MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | PROJECTILE MOTION |
| SL ARORA | Problen Solution |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
A particle of mass 100 g is fired with a velocity of `20 ms^(-1)` making an angle of `30^(@)` with horizontal. When it rises to the point of its highest point, find the change in its momentum.
View SolutionA body of mass m is projected with velocity v at an angle of `45^(@)` with the horizontal. Find the change in its momentum at the end of flight.
View SolutionThe height y and the distance x along the horizontal plane of projectile on a certain planet (with no atmosphere on it) are given by y = `(8t-5t^(2))` metre and x = 6t metre , where time t is in seconds. Find the initial velocity with which the projectile is projected.
View SolutionShow that the motion of one projectile as seen from another projectile will always be a straight line motion.
View SolutionA particle is projected horizontal with a speed u from the top of plane inclined at an angle `theta` with the horizontal. How far from the point of projection will the particle strike the plane?
View SolutionA helicopter on a flood relief mission flying horizontally with a speed u at a altitude h, has to drop a food packet for a victim standing on the ground. At what distance from the victim should the food packet be dropped ?
View SolutionA ball is thrown from ground level so as to just clear a wall 4m high at a distance of 4 m and falls at a distance of 14 m from the wall. Find the magnitude and direction of the initial velocity.
View SolutionA ball rolls off the top of a staircase with a horizontal velocity `u m//s`. If the steps are h meter high and b meter wide, the ball will hit the edge of the nth steps, if:
View SolutionA particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If `alpha` and `beta` be the base angles and `theta` the angle of projection, prove that `tan theta = tan alpha + tan beta`.
View SolutionA particle is projected with velocity `2 sqrt(gh)` so that it just clears two walls of equal height h which are at a distance 2h from each other. Show that the time of passing between the walls is `2 sqrt(h//g)`.
View SolutionA shell is fired from a gun from the bottom of a hill along its slope. The slope of the hill is `alpha = 30^(@)`, and the angle of the barrel to the horizontal `beta = 60^(@)`. The initial velocity u of the shell is `21 ms^(-1)`. Find the distance from the gun to the point at which the shell falls.
View SolutionIf the horizontal range of a projectile be a and the maximum height attained by it is b, then prove that the velocity of projection is
View SolutionThe velocity of a projectile when it is at the greatest height is `(sqrt (2//5))` times its velocity when it is at half of its greatest height. Determine its angle of projection.
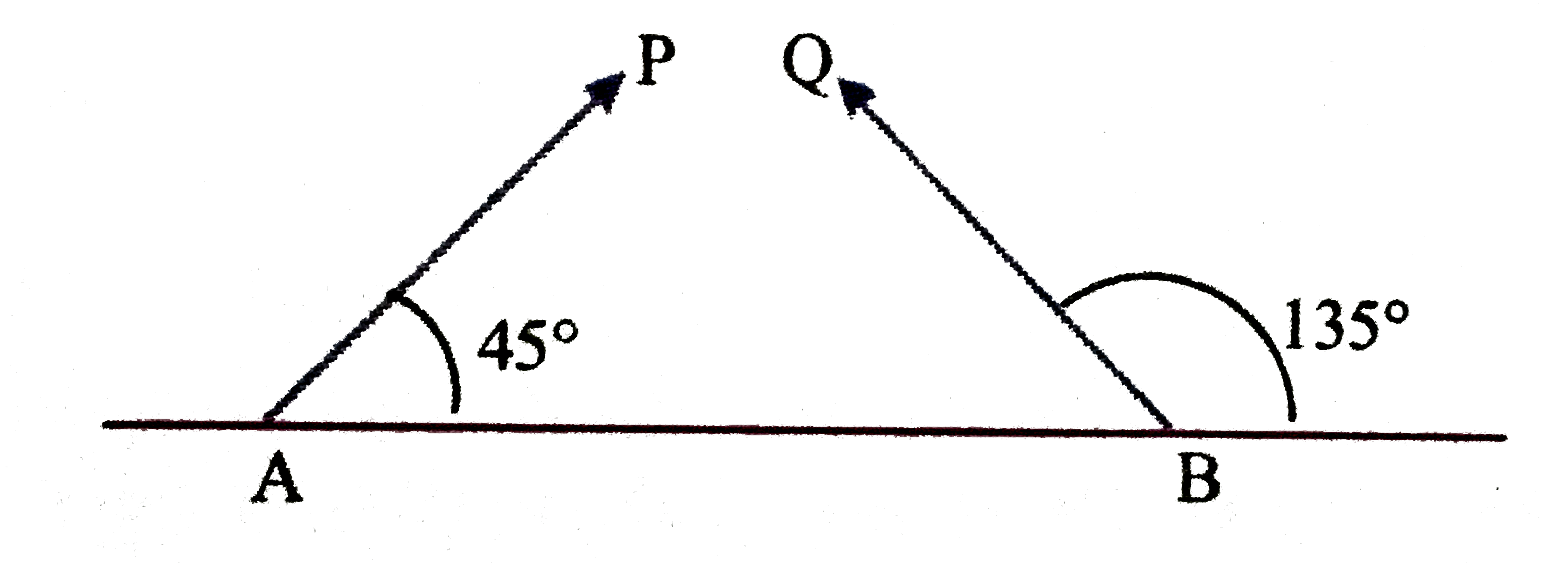
View SolutionParticles `P` and `Q` of masses `20g` and `40g`, respectively, are projected from positions `A` and `B` on the ground. The initial velocities of `P` and `Q` make angles of `45^(circ)` and `135^(circ)`, respectively with the horizontal as shown in the fig. Each particle has an initial speed of `49m//s`. The separation `AB` is `245m`. Both particles travel in the same vertical plane and undergo a collision. After the collision `P` retraces its path. The separation of `Q` from its initial position when it hits the ground is
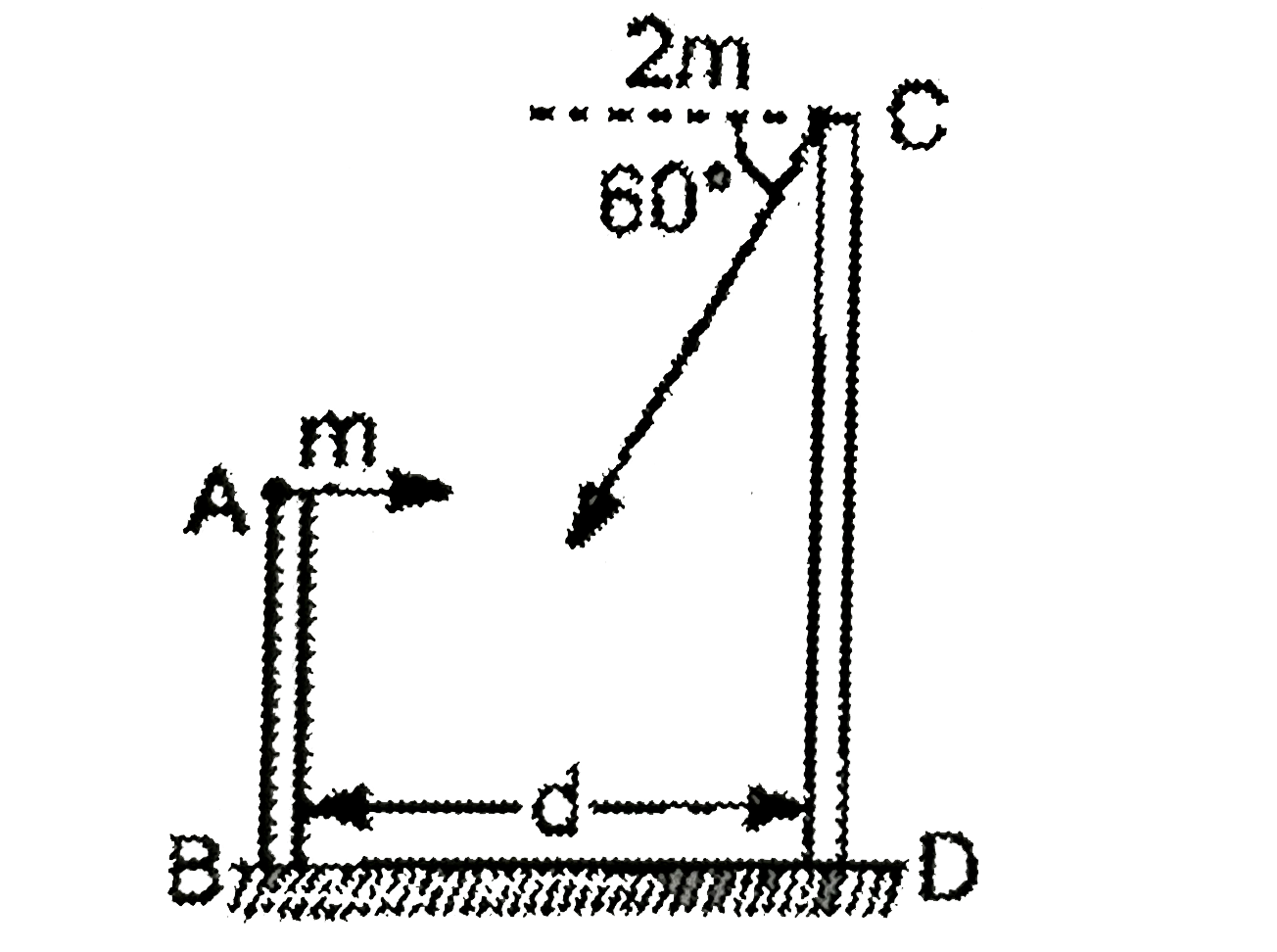
View SolutionTwo towers AB and CD are situated a distance d apart as: shown in Fig. 1E.139 (a). AB is 20 m high and CD is 30 m high from the ground. An object of mass mis thrown from the top of AB horizontally with a velocity of 10 m/s towards CD.
Simultaneously another object of mass 2m is thrown from the ·top of CD at an angle of `60^(@)` to the horizontal towards AB with the same magnitude of initial velocity as that of the_ first' objects . The two objects move in the same vertical plane, collide in mid-air and stick to each other.
Calculate the distance d between the towers.
View SolutionA bullet of mass M is fired with a velocity `50m//s` at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length `10//3` metres and gets embeded in the bob. After the collision, the string moves through an angle of `120^@`. Find
(i) the angle `theta`,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take `g=10 m//s^2`
View SolutionTwo guns situated at the top of a hill of height `10 m` fire one shot each with the same speed `5sqrt(3) m//s` at some interval of time. One gun fires horizontal and the other fores upwards at an angle of `60^(@)` with the horizontal. Two shots collide in air at a poit `P`. Find (i) time-interval between the firing and (ii) coordinates of the point `P`. Take the origin of coordinates system at the foot of the hill right below the muzzle and trajectorise in the `x-y` plane.
View Solution
Problen Solution questions and complete solutions for chapter PROJECTILE MOTION of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11