Complete Solutions to EXAMPLE of chapter Work, Energy and power of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Work, Energy and power |
| SL ARORA | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
How is work done measured when, The force acts along the direction of motion of the body
View SolutionHow is work done measured when, The force is inclined to the direction of motion of the body?
View SolutionWhat is meant by positive work, negative work and zero work ? Illustrate your answer with two examples of each type.
View SolutionWrite the dimensional formula of work.
View SolutionDefine absolute and gravitational units of force state relation between them .
View SolutionWrite an expression for work done in terms of rectangular components of force and displacement.
View SolutionA gardener pushes a lawn roller through a distance of 20 m. If he applies a force of 20 kg wt in a direction inclined at `60^(@)` to the ground , find the work
View SolutionA person is holding a bucket by applying a force of 10 N. He moves a horizontal distance of 5 m and then climbs up a vertical distance of 10 m. Find the total work done him.
View SolutionA cyclist comes to a skidding stop in `10m`. During this process, the force on the cycle due to the road is `200N` and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?
View SolutionA cyclist comes to a skidding stop in `10m`. During this process, the force on the cycle due to the road is `200N` and is directly opposite to the motion.
a. How much work does the road do on the cycle?
b. How much work does the cycle do on the road?
View SolutionA force `oversetrightarrowF=hati+5hatj+7hatk` acts on a particle and displaces it through `oversetrightarrows=6hati+9hatk`. Caldulate the work done if the force is in newton and displacement in metre.
View SolutionA force `vecF(yhatl+xhatJ),` where K is a positive constant, acts on a particle moving in the XY-Plane. Starting from the origin, the particle is taken along the positive X-axis to a point (a,0) and then parallel to the y-axis to the point (a,a). Calculate the total work done by the force on the particle.
View SolutionA uniform chain of length 2 m is kept on a table such that a length of 60 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg. What is the work done in pulling the entire chain on the table?
View SolutionCalculate the work done in raising a stone of mass 5 kg and specific gravity 3, lying at the bed of a lake through a height of 5 m.
View SolutionA cluster of clouds at a height of 1000m above the earth burst and enough rain fell to cover an area of `10^(6)m^(2)` with a depth of 2cm. How much work would have been done in raising water to the height of clouds ? Take `g=10m//s^(2)` and density of water `10^(3)kg//m^(3)`.
View SolutionA 2kg particle starts at the origin and moves along the positive x-axis. The net force acting on it measured at intervals of 1 m : 27.9, 28.3, 30.9, 34.0, 34.5, 46.9, 48.2, 50.0, 63.5, 13.6, 12.2, 32.7, 46.6 and 27.0 (in newtons). What is the total work done on the particle in this interval?
View SolutionA body moves from point A to B under the action of a force, varying in magnitude as shown in figure. Obtain the work done. Force is expressed in newton and displacement in meter.

View SolutionA woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100N over a distance of 10m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50N. The total distance through which trunk has been moved is 20m. Plot the force applied by the woman and the frictional force, which is 50N against the distance. Calculat the work done by the two forces over 20m.
View SolutionA particle moves along the X-axis from x=0 to x=5 m under the influence of a force given by `F=7-2x+3x^(2).` Find the work done in the process.
View SolutionDefine the term energy. What are its units and dimensions? Name the different forms of energy.
View Solution(a) What is mechanical energy ? (b) What is electromagnetic energy ?
View SolutionDefine kinetic energy. Give some examples of bodies possessing kinetic energy.
View SolutionWhat do you mean by kinetic energy ? Derive an expression for the kinetic energy of an object of mass m moving with velocity, `upsilon.`
View SolutionWORK ENERGY THEOREM
View SolutionWORK ENERGY THEOREM
View SolutionA toy rocket of mass 0.1 kg hass a small fuel of mass 0.02 kg, which it burns out in 3s. Starting from rest on a horizontal smooth track, it gets a speed of `20ms^(-1)` after the fuel is burnt out. What is the approcimate thrust of the rocket ? What is the energy content per unit mass of the fuel ? (Ignore the small mass variation of teh rocket during fuel burning).
View SolutionA bullet weighing 10 g is fired with a velocity of `800 ms^(-1)`. After passing through a mud wall 1 m thick, its velocity decreases to `100 ms^(-1)`. Find the average resistance offered by the mud wall.
View SolutionA shot travelling at the rate of `100 ms^(-1)` is just able to pierce a plank 4 cm thick. What velocity is required to just pierce a plank 9 cm thick ?
View SolutionIn a ballistics demonstration, a police officer fires a bullet mass `50.0g` with speed `200ms^(-1)` on soft plywood of thickness 2.00cm. The bullet emerges only with `10%` of its initial kinetic energy. What is the emergent speed of the bullet ?
View SolutionIt is well known that a rain drop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop, but is otherwise undetermined. Consider a drop of mass 1.0g falling from a height of 1.00km. It hits the ground with a speed of `50.0ms^(-1)` (a) What is the work done by the gravitational force ? (b) What is the work done by the unknown resistive force ?
View SolutionA block of mass `m=1kg` moving on a horizontal surface with speed `v_(i)=2ms^(-1)` enters a rough patch ranging from `x0.10m to x=2.01m`. The retarding force `F_(r)` on the block in this range ins inversely proportional to x over this range
`F_(r)=-(k)/(x) fo r 0.1 lt xlt 2.01m`
`=0` for `lt 0.1m` and `x gt 2.01m` where `k=0.5J`. What is the final K.E. and speed `v_(f)` of the block as it crosses the patch?
View SolutionTwo identical 5 kg blocks are moving with same speed of `2m//s` towards eachother along a frictionless horizontal surface. The two blocks collide, stick together and come to rest. Consider the two blocks as a system. Caluculate work done by (i) external forces (ii) internal forces.
View SolutionTwo identical 5 kg blocks are moving with same speed of `2m//s` towards eachother along a frictionless horizontal surface. The two blocks collide, stick together and come to rest. Consider the two blocks as a system. Caluculate work done by (i) external forces (ii) internal forces.
View SolutionIf the linear momentum of a body increases by 20%, what will be the % increase in the kinetic energy of the body ?
View SolutionIf the kinetic energy of kinetic energy of a body increases by 300%, by what % will the linear momentum of the body rease ?
View SolutionA body of mass `0.3kg` is taken up an inclined plane of length `10m` and height `5m,` and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is `0.15`.
What is the
(a) work done by the gravitational force over the round trip ?
(b) work done by the applied force on the upward journey ?
(c) work done by the frictional force over the round trip ,
(d)kinetic energy of the body at the end of the trip ?
View SolutionA body of mass `0.3kg` is taken up an inclined plane of length `10m` and height `5m,` and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is `0.15`.
What is the
(a) work done by the gravitational force over the round trip ?
(b) work done by the applied force on the upward journey ?
(c) work done by the frictional force over the round trip ,
(d)kinetic energy of the body at the end of the trip ?
View SolutionA body of mass `0.3kg` is taken up an inclined plane of length `10m` and height `5m,` and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is `0.15`.
What is the
(a) work done by the gravitational force over the round trip ?
(b) work done by the applied force on the upward journey ?
(c) work done by the frictional force over the round trip ,
(d)kinetic energy of the body at the end of the trip ?
View SolutionA body of mass 0.3 kg is taken up an inclined plane to length 10 m and height 5 m, and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is 0.15. What is the kinetic energy of the body at the end of the trip?
View SolutionWhat is meant by the term potential energy ? Give its two examples.
View SolutionMention some common types of petential energy?
View SolutionWhat do you mean by gravitational potential energy ? Derive an expression for the gravitational potential energy of an object raised to a height h .
View SolutionCONSERVATIVE FORCES
View SolutionExplain qualitatively that how is the gravitational force a conservative force?
View SolutionWhat are conservative and non-conservative forces, explain with examples. Mention some of their properties.
View SolutionDefine potential energy in context with a conservative force. How can these two quantities be determined from each other ? Write the necessary relations?
View SolutionShow analytically that gravitational force is a conservative force.
View SolutionSTATEMENT-1 : Mechanical energy is the sum of macroscopic kinetic & potential energies.
STATEMENT-2 : Mechanical energy is that part of total energy which always remain conserved.
View SolutionCONSERVATIVE FORCES
View SolutionShow that the total mechanical energy of a freely falling body remains constant throughout its fall?
View SolutionA vehicle of mass `15` quintal climbs up a hill `200 m` high. It then moves on a level road with a speed of `30 ms^(-1)`. Calculate the potential energy gained by it and its total mechanical energy while running on the top of the hill.
View SolutionCalculate the velocity of the bob of a simple pendulum at its mean position if it is able to rise to a vertical height of 10 cm. Take `g=9.8 ms^(-2)`.
View SolutionA girl of mass 40 kg sits in a swing formed by a rope of 6 m length. A person pulls the swing to a side so that the rope makies an angle of `60^(@)` with the vertical. What is the gain in potential energy of the girl ?
View SolutionHow high must a body be lifted to gain an amount of potential energy equal to the kinetic energy it has when moving at speed `20 ms^(-1)`? The value of acceleration due to gravity at a pleace is `g=9.8 ms^(-2)` .
View SolutionThe string of a pendulum is `2.0m` long. The bob is pulled sideways so that the string becomes horizontal and then the bob is released. What is the speed with which the bob arrives at the lowest point ? Assume theat `10%` of initial energy is dissipated against air resistance. Take `g=10m//s^(2)`
View SolutionA ball bounce of `80%` of its original height . What fraction of its mechanical energy is lost in each bounce ?
View SolutionA ball at rest is dropped from a height of 12m. It loses 25% of its kinetic energy in striking the ground, find the height to which it bounces. How do you account for the loss in kinetic energy ?
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_0` at the lowest point a such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost poin, C. This is shown in Figure. Obtain an expression for `v_0`
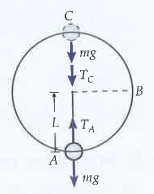
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(0)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) `v_(0)` (ii) the speeds at points B and C, (ii) the ration of kinetic energies `(K_(B)//K_(C))` at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
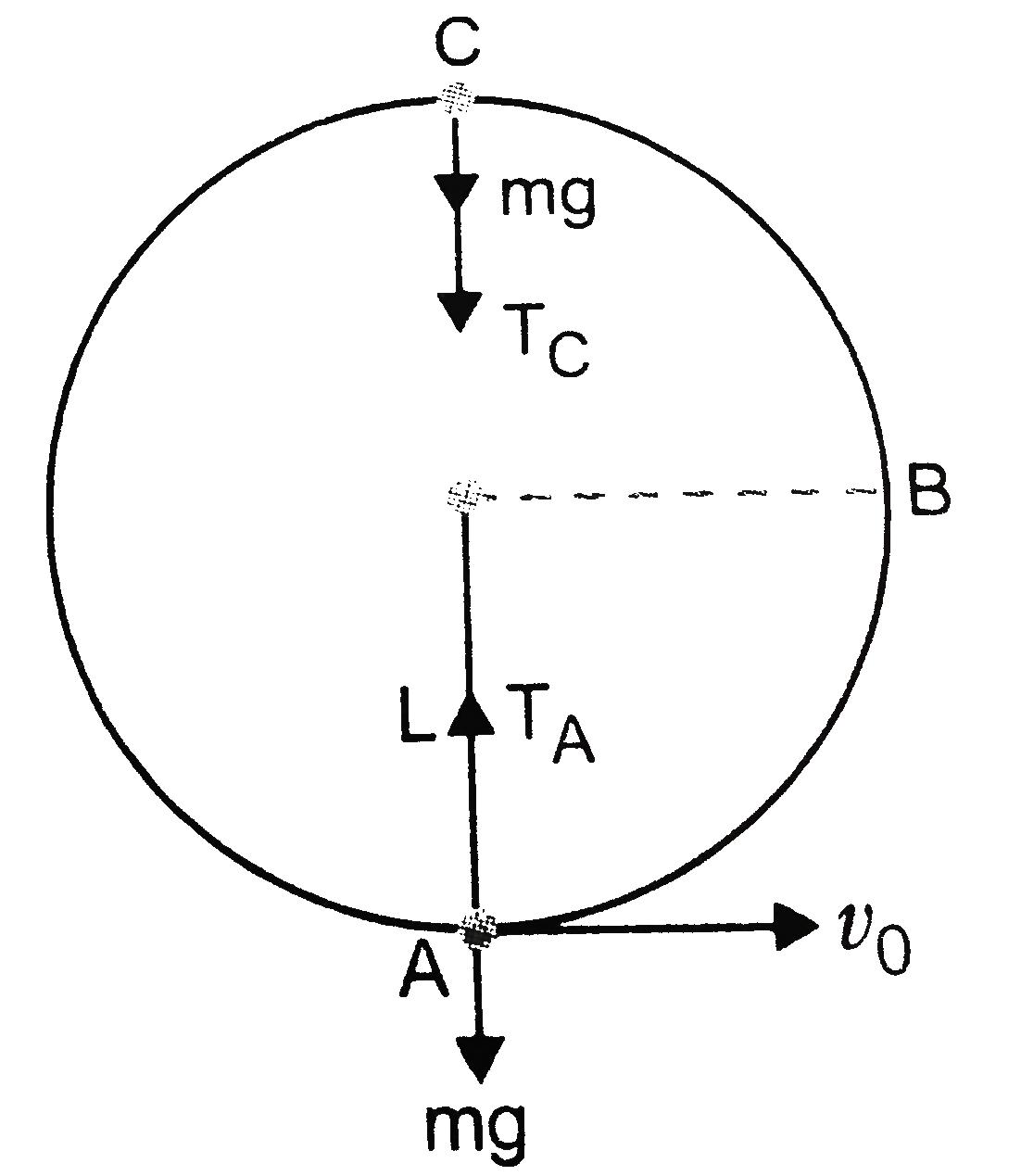
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(0)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) `v_(0)` (ii) the speeds at points B and C, (ii) the ration of kinetic energies `(K_(B)//K_(C))` at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.

View SolutionA ball falls under gravity from a height of 10 m with an initial downward velocity u. It collides with the ground, losses 50% of its energy in collision and then rises back to the same height. The initial velocity u is
View SolutionShow that the elastic force of a spring is a conservative forcce. Hence write an ex,pression for the petenial energy of an elastic stretched spriing.
View SolutionDraw a plot of spring force `F_s` and displacement x. Hence find an expresion for the P.E. of an elatic stretched spring,
View SolutionTwo springs have force constants `k_(1) " and " k_(2) (k_(1) gt k_(2))`. On which spring is more work done, if (i) they are stretched by the same force and (ii) they are stretched by the same amount ?
View SolutionTwo springs have force constants `k_(1) " and " k_(2) (k_(1) gt k_(2))`. On which spring is more work done, if (i) they are stretched by the same force and (ii) they are stretched by the same amount ?
View SolutionThe length of a steel wire increases by `0*5cm` , when it is loaded with a weight of `5*0kg`. Calculate force constant of the wire and workdown in stretching the wire. Take `g=10ms^(-1)`.
View SolutionThe length of a steel wire increases by `0*5cm` , when it is loaded with a weight of `5*0kg`. Calculate force constant of the wire and workdown in stretching the wire. Take `g=10ms^(-1)`.
View SolutionThe potential energy of a certain spring when stretched through a distance 'S' is `10` joule. The amount of work (in joule) that must be done on this spring to stretch it through an additional distance 'S' will be
View SolutionTo stimulat car accidents, the auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000kg moving with a speed of `18.0 km//h` on a smooth road and colliding with a horizontally mounted spring of spring constant `6.25xx10^(3)Nm^(-1)`. What is the maximum compression of the spring?
View SolutionA spring of force constant 24N`//`m is resting on a frictionless horizontal surface. A force of 10N is applied on the block of mss 4kg at one end of the spring. What is the speed of the block when it has been moved through a distance of 0.5 m ?
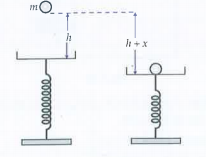
View SolutionA ball of mass m is dropped from a height h on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. What is the spring constant k?
View SolutionA block of mass 2 kg initially at rest is dropped from a height of 1m into a vertical spring having force constant `490 Nm^(-1)`. Calculate the maximum distance through which the spring will be compressed.
View SolutionDescribe the verious forms of energy?
View SolutionWhat is Einstein's mass-energy equivvalence? Mention some of its practical applications?
View SolutionState and explain the principle of conservation of energy?
View SolutionThe energy required to break one bond in DNA is `10^(-20)J`. This value in `eV` is nearly:
View SolutionExpress (a) the energy required to break one bond in DNA `(10^(-10)J)` in eV.
(b) the kinetic energy of an air molecule `(10^(-21)J)` in eV.
(c) the daily intake of a human adult `(10^(7)J)` in kilocalories.
View SolutionExpress (a) the energy required to break one bond in DNA `(10^(-10)J)` in eV.
(b) the kinetic energy of an air molecule `(10^(-21)J)` in eV.
(c) the daily intake of a human adult `(10^(7)J)` in kilocalories.
View SolutionHow much mass is converted into tenergy per day in a nuclear power plant operated at `10^(7)` kW?
View SolutionIf `1000kg` of water is heated from `0^(@)C` to `100^(@)C`, calculate the increase in mass of water.
View SolutionCalculate the energy in MeV equivalent to the rest mass of an electron . Given that the rest mass of an electron , `m=9.1 xx 10^(-31) kg`, `1MeV = 1.6 xx 10^(-13) J` and speed of light , `c= 3 xx 10 ^(8) ms ^(-1)`.
View SolutionExtimate the amount of energy released in the following nuclear fusion reaction. `overset(2)(1)H+overset(2)(1)Hrightarrowoverset(3)(2)He+overset(1)(0)n` Given mass of `overset(2)(1)H=2.0141` amu, mass of `overset(3)(2)He=3.0160` amu, mass of `overset(1)(0)n=1.0087` amu and 1 amu =`1.661xx10^(-27)kg`. Express your answer in units of MeV?
View SolutionWhen slow neutrons are incident on a target containing `underset(92)overset(235).U`, a possible fission reaction is
`underset(92)overset(235).U+underset(0)overset(1).nrarr underset(56)overset(141).Ba+underset(36)overset(92).Kr+3_(0)^(1)n`
Estimate the amount of energy released using the following data Given, mass of `underset(92)overset(235).U=235.04 amu`, mass of `underset(0)overset(1).n=1.0087 amu`, mass of `underset(56)overset(141).Ba=140.91 amu`, mass of `underset(36)overset(92).Kr=91.926 amu`, and energy equivalent to 1 amu=931 MeV.
View SolutionDefine the term power. Is it a scalar or vector quantity? Give its dimensions and units.
View SolutionDefine instantaneous power. Express it as the scalar product of force and velocity vectors.
View SolutionOf which physical quantity is the unit kilowatt hour? Define one kilowatt hour. Express it in joules.
View SolutionA man weighing 60 kg climbs up a staircase carrying a load of 20 kg on his head. The stair case has 20 steps each of height 0.2 m. If he takes 10 s to climb find his power
View SolutionA car of mass `2000kg` is lifted up a distance of `30m` by a crane in 1 minute . A second crane does the same job in 2 minues. Do the cranes consume the same or different amounts of fuel ? What is the power supplied by each crane ? Neglect power disspation against friction.
View SolutionThe human heart discharges 75ml of blood at each beat against a pressure of 0.1m of Hg. Calculate the power of the heart assuming that the pulse frequency is 80 beats per minute. Given, density of mercury `=13.6xx10^(3) kg//m^(3)`
View SolutionAn electric motor is used to lift an elevator and its load (total mass 1500kg) to a height of 20m. The time taken for the job is 20s. What work is done ? What is the rate at which work is done. If efficiency of the motor is `75%`, at which rate is the energy supplied to the motor?
View SolutionCalculate the horse power of a man who can chew ice at the rate of `60g min.^(-1)`. Given `J = 4.2 J cal^(-1)` and altent heat of ice `= 80 cal g^(-1), 1hp = 746W`.
View SolutionA machine gun fires 60 bullets per minute with a velocity of `700ms^(-1)`. If each bullet has a mass of 50g, find the power of the gun.
View SolutionAn elevator can carry a maximum load of `1800 kg` (elevator + passengers) is moving up with a constant speed of `2 ms^(-1)`. The friction force opposite the motion is `4000 N`.What is minimum power delivered by the motor to the elevator?
View SolutionA well `20m` deep and `3m` is diameter contains water to a dept of `14m`. How long will a `5 hp` engine take to empty it ?
View SolutionThe turbine pits at Niagra Falls are 50m deep. The average horse power develop is 5000. If the efficiency of the generator `85%` , how much water passes through the turbine per minute ? Take `g=10m//s^(2)`.
View SolutionA man cycles up a hill whose slope is 1 in 20 with a velocity of `6.4 km h^(-1)` along the hill. The weight of the man and the cycle is 98kg. What work per minute is the man doing ? What is his horse power ?
View SolutionIn elastic collision,
View SolutionIn an inelastic collision
View SolutionWhich of the following is not a perfectly inelastic collision
View SolutionDefine the terms : head- on collision and oblique collision
View Solution
EXAMPLE questions and complete solutions for chapter Work, Energy and power of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11