A 2kg particle starts at the origin and moves along the positive x-axis. The net force acting on it measured at intervals of 1 m : 27.9, 28.3, 30.9, 34.0, 34.5, 46.9, 48.2, 50.0, 63.5, 13.6, 12.2, 32.7, 46.6 and 27.0 (in newtons). What is the total work done on the particle in this interval?
To find the total work done on the particle as it moves along the positive x-axis, we will follow these steps:
Step 1: Understand the relationship between work, force, and displacement
The work done W by a force F over a displacement s is given by the formula:
W=F⋅s
In this case, since the force is acting in the direction of displacement, we can simplify this to:
W=F×s
where s is the displacement.
Step 2: List the forces and displacements
The net forces acting on the particle at each 1-meter interval are given as:
- F1=27.9N
- F2=28.3N
- F3=30.9N
- F4=34.0N
- F5=34.5N
- F6=46.9N
- F7=48.2N
- F8=50.0N
- F9=63.5N
- F10=13.6N
- F11=12.2N
- F12=32.7N
- F13=46.6N
- F14=27.0N
Since the displacement for each interval is s=1m, we can use this value for all calculations.
Step 3: Calculate the total work done
The total work done WT can be calculated by summing the work done in each interval:
WT=(F1+F2+F3+F4+F5+F6+F7+F8+F9+F10+F11+F12+F13+F14)×s
Substituting s=1m:
WT=(27.9+28.3+30.9+34.0+34.5+46.9+48.2+50.0+63.5+13.6+12.2+32.7+46.6+27.0)×1
Step 4: Perform the addition
Now, let's calculate the sum:
WT=27.9+28.3+30.9+34.0+34.5+46.9+48.2+50.0+63.5+13.6+12.2+32.7+46.6+27.0
Calculating this step-by-step:
- 27.9+28.3=56.2
- 56.2+30.9=87.1
- 87.1+34.0=121.1
- 121.1+34.5=155.6
- 155.6+46.9=202.5
- 202.5+48.2=250.7
- 250.7+50.0=300.7
- 300.7+63.5=364.2
- 364.2+13.6=377.8
- 377.8+12.2=390.0
- 390.0+32.7=422.7
- 422.7+46.6=469.3
- 469.3+27.0=496.3
Thus, the total work done is:
WT=496.3J
Final Answer
The total work done on the particle in the given interval is 496.3J.
The work done W by a force F over a displacement s is given by the formula:
W=F⋅s
In this case, since the force is acting in the direction of displacement, we can simplify this to:
W=F×s
where s is the displacement.
The net forces acting on the particle at each 1-meter interval are given as:
- F1=27.9N
- F2=28.3N
- F3=30.9N
- F4=34.0N
- F5=34.5N
- F6=46.9N
- F7=48.2N
- F8=50.0N
- F9=63.5N
- F10=13.6N
- F11=12.2N
- F12=32.7N
- F13=46.6N
- F14=27.0N
The total work done WT can be calculated by summing the work done in each interval:
WT=(F1+F2+F3+F4+F5+F6+F7+F8+F9+F10+F11+F12+F13+F14)×s
Substituting s=1m:
WT=(27.9+28.3+30.9+34.0+34.5+46.9+48.2+50.0+63.5+13.6+12.2+32.7+46.6+27.0)×1
Now, let's calculate the sum:
WT=27.9+28.3+30.9+34.0+34.5+46.9+48.2+50.0+63.5+13.6+12.2+32.7+46.6+27.0
Calculating this step-by-step:
- 27.9+28.3=56.2
- 56.2+30.9=87.1
- 87.1+34.0=121.1
- 121.1+34.5=155.6
- 155.6+46.9=202.5
- 202.5+48.2=250.7
- 250.7+50.0=300.7
- 300.7+63.5=364.2
- 364.2+13.6=377.8
- 377.8+12.2=390.0
- 390.0+32.7=422.7
- 422.7+46.6=469.3
- 469.3+27.0=496.3
WT=496.3J
The total work done on the particle in the given interval is 496.3J.
Topper's Solved these Questions
Similar Questions
Only one force is acting on a 2.8 kg particle-like object whose position is given by x=4.0t−5.0t2+2.0t3, with x in meters and t in seconds. What is the work done by the force from t=0 to t=6.0 s ?
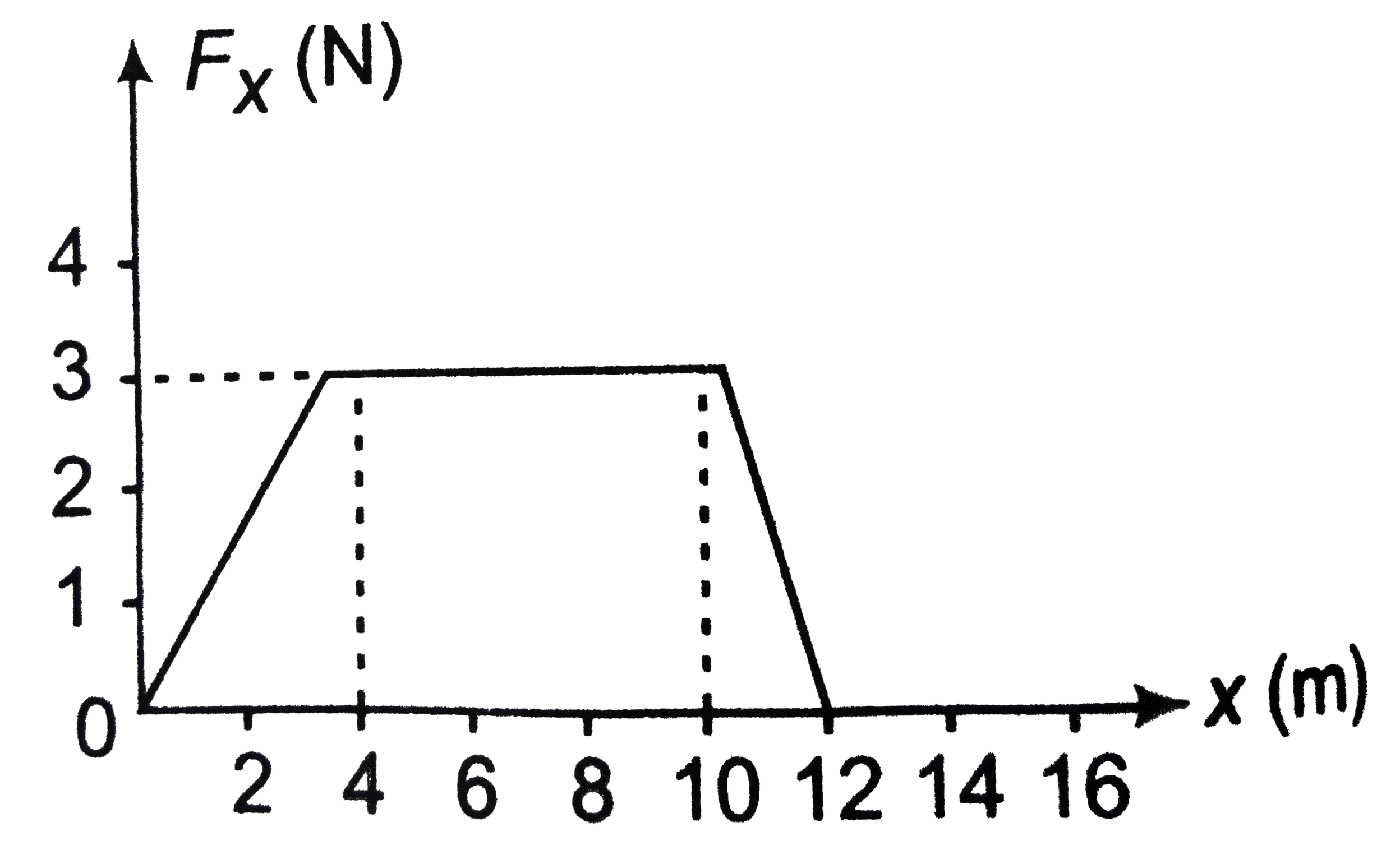
View SolutionA particle is subjected to a force Fx that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from x=10.0m to x=5.0m,
(b) from x=5.0m to x=10.0m,
(c ) from x=10.0m to x=15.0m,
(d) what is the total work done by the force over the distance x=0 to x=15.0?
 .
.
View Solution
Knowledge Check
What is the median of the numbers 4.6,0,9.3,−4.8,7.6,2.3,12.7,3.5,8.2,6.1,3.9,5.2?
A3.8B4.9C5.7D6What is the median of a numbers 4.6, 0, 9.3.-4.8. 7.6. 23. 12.7.3.5, 8.2,6.1,3.9, 5.2
AA. 3.8BB. 17.85CC. 15.7DD. 6In the following series is written in the reverse order, which number will be the fourth to the right of the seventh number from the left?
7,3, 9, 7,0,3, 8, 4,6, 2, 1, 0, 5, 11, 13.A0B5C9D11
The weights of 9 boxes in kgms are as follows:
27.5, 31.2, 28.0, 32.0, 29.8, 30.3, 92.0, 28.7, 31.5
Find the appropriate average weight of the boxes.
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionWhat is the LCM of 13,56,29,427?
View SolutionA particle of mass 3 kg is moving along x - axis and its position at time t is given by equation x=(2t2+5)m. Work done by all the force acting on it in time interval t=0 to t=3s is
View SolutionThe position (x) of a particle of mass 1 kg moving along X-axis at time t is given by (x=12t2) metre. Find the work done by force acting on it in time interval from t=0 to t=3s.
View Solution
