Complete Solutions to EXAMPLE of chapter System of particles & rotational Motion of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | System of particles & rotational Motion |
| SL ARORA | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
What is meant by a particle, a system and internal and external Force?
View SolutionWhat do you meant by centre of mass of a system? How does its differ from centre of gravity?
View SolutionObtain an expression for the position vector of centre of mass of a two particle system.
View SolutionWrite an expression for the position vector of the centre of mass of n-particle system. Also write the equations of motion which govern the motion of the centre of mass
View SolutionShow that in the absence of any external force, the velocity of the centre of mass remains constant.
View SolutionShow that the total linear momentum of a system of particles is conserved in the absence of any external force. Also show that total linear momentum of the system is equal to the product of the total mass of the system and the velocity of its centre of mass.
View SolutionFind the centre of gravity of a triangular lamina, each side of which measures `9sqrt(3)` cm
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionTwo particle of masses 100g and 300 g at a given time have positions `2 hat(i)+5hat(j)+13 hat(k) and -6hat(i)+4hat(j)-2hat(k)`m respectively and velocities `10 hat(i)-7hat(j)-3hat(k)and 7 hat(i)-9hat(j)+6 hat(k) "ms"^(-1)` respectively. Determine the instantaneous position and velocity of CM.
View SolutionIf three point masses `m_(1),m_(2) and m_(3)` are situated at the vertices of an equilateral triangle of side a, then what will be the co-ordinates of the centre of mass of this system ?
View SolutionFind the position of centre of mass of the T-shaped plate from `O`, in Fig.

View SolutionFind the centre of mass of a uniform `L` shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is `3kg`.

View SolutionA uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
View SolutionA square of side `4 m` having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre `O`.
View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
View SolutionDetermine the position of the centre of mass of a hemisphere of radius R.
View SolutionDetermine the coordinate of the centre of mass of a right circular solid cone of base radius R and height h.
View SolutionWhat is a rigit body? Give Examples.
View SolutionOn what factors does the position of cm of a rigid body depend ?
View SolutionWhat do you mean by rotational motion of a rigid body?
View SolutionOn the application of a constant torque , a wheel is turned from rest through 400 radians in 10 s. The angular acceleration is :
View SolutionANGULAR ACCELERATION
View SolutionThe angular speed of a motor wheel is increased from 120 rpm to 3120 rpm in 16 seconds. The angular acceleration of the motor wheel is
View SolutionA constant torque is acting on a wheel. If starting from rest, the wheel makes n rotations in t seconds, show that the angular
acceleration is given by `alpha = (4pi n)/(t^(2)) rad s^(-2)`.
View SolutionThe radius of a wheel of car is `0.4m`. The car is accelerated from rest by an angular acceleration of `1.5 rad//s^(2)` for `20 s`. How much distance will the wheel cover in this time and what will be its linear velocity ?
View SolutionThe turning effect of the applied force does NOT depend upon
View SolutionFind the term of an A.B is p and its common difference is q. Find its 10^th trem
View SolutionState and explain the principle of moments of rotational equilibrium. Define mechanical advantage.
View SolutionWhat is a couple ? What effect does it have on a body ?
View SolutionObtain an expression for work done by a gas in an isothermal expansion.
View SolutionExplain how torque can be expressed as a vector product of two vectors. How is the direction of torque determined ?
View SolutionDefine the term angular momentum. Give its units and dimensions.
View SolutionThe relation between the torque `tau` and angular momentum L of a body of moment of inertia I rotating with angular velocity `omega` is
View SolutionProve that the angular momentum of a particle is equal to twice the product of its mass and areal velocity.
View SolutionProve that the rate of change of total angular momentum of a system of particles is equal to the total torque acting on the system.
View Solution(i) Find the torque of a force `7hati + 3hatj - 5hatk` about the origin. The force acts on a particle whose position vector is `hati - hatj + hatk`.
(ii) Show that moment of a couple does not depend on the point about which you take the moments.
View SolutionA metal bar `70 cm` long and `4.00 kg` in mass is supported on two knife edges placed `10 cm` from each end. A `6.00 kg` weight is suspended at `30 cm` from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
View SolutionA particle of mass `m` is released from rest from point `P` at `x = x_(0)` on X-axis from origin `O` and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time `t`, when it is at the point `Q w.r.t.O` ?
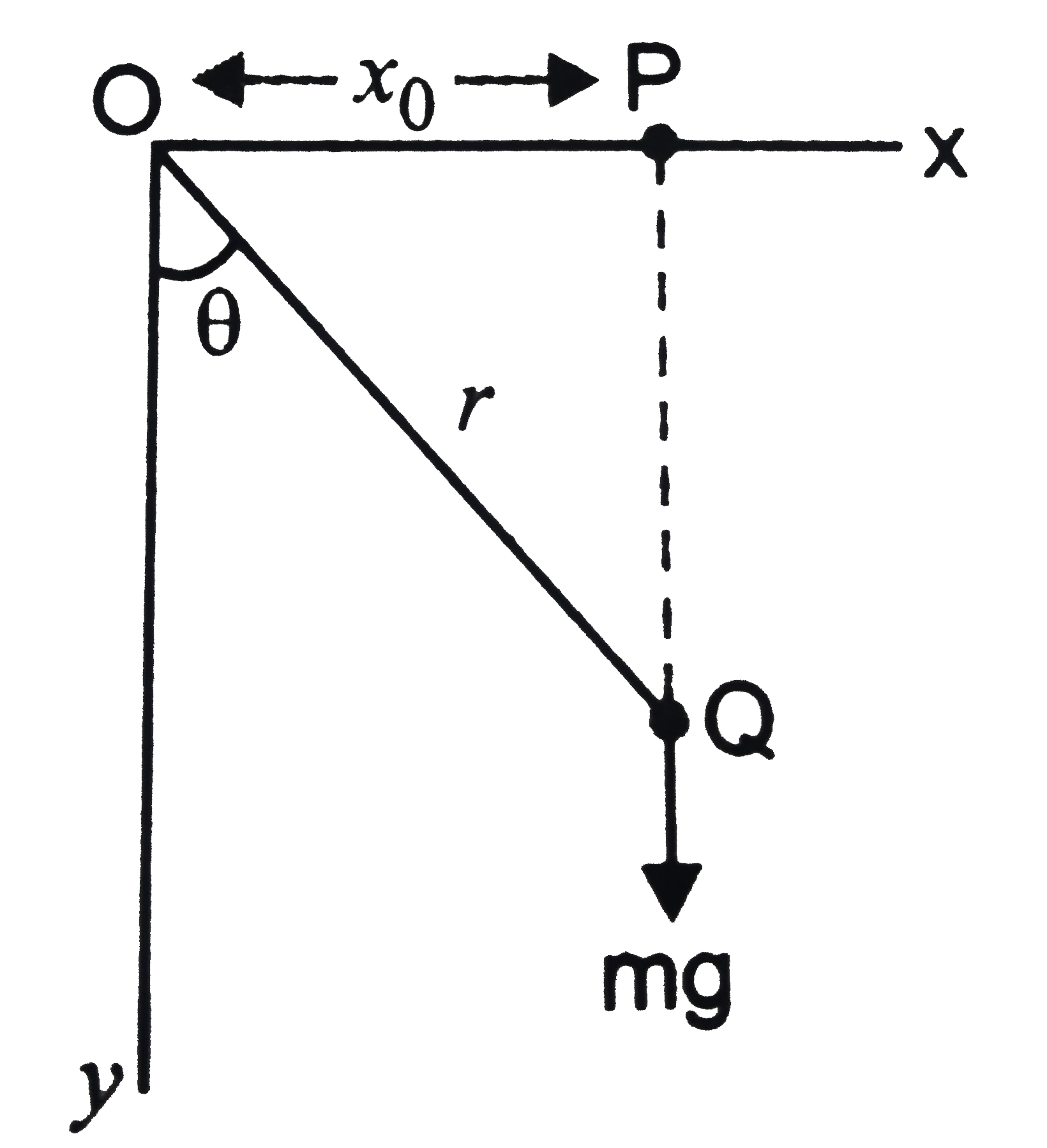
View SolutionA particle of mass `m` is released from rest from point `P` at `x = x_(0)` on X-axis from origin `O` and falls vertically along y-axis as shown in Fig. What is the magnitude of the torque acting on the particle at time `t`, when it is at the point `Q w.r.t.O` ?

View SolutionAn electron of mass `9 xx 10^(-31)` kg revolves in a circle of radius 0.53 Å around the nucleus of hydrogen with a velocity of `2.2 xx 10^(6) "ms"^(-1)`. Show that its angular momentum is equal to `h//2pi`, where `h` is Plank's constant of value `6.6 xx 10^(-34) Js`.
View SolutionShow that angular momentum of a satellite of mass `M_(s)` revolving around earth of mass `M_(e)` in an orbit of radius `r` is `sqrt(GM_(s)^(2)M_(e)r)`.
View SolutionDefine a rigid body. What is meant by the term equilibrium ?
View SolutionDistinguish between stable, unstable and neutral equilibria of a body.
View SolutionMoment of inertia of a body depends upon
View SolutionWhat are the factors on which moment of inertia of a body depend ?
View SolutionMention some practical applications which make use of the property of moment of inertia
View SolutionA body is rotating with uniform angular velocity w about an axis. Establish the formula for its kinetic energy of rotation. Define moment of inertia of the body with respect to the axis of rotation on this basis
View SolutionThe radius of gyration of a body depends upon
View SolutionState and prove theorem of perpendicular axes.
View SolutionState and prove theorem of parallel axes.
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionWhat is the moment of inertia of a uniform circular ring about its diameters ?
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionWhat is the moment of inertia of a uniform circular ring about its diameters ?
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionState the expression for the moment of inertia of a thin uniform disc about an axis perpendicular to its plane and through its centre. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane.
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionDerive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionMoment of inertia of a hollow cylinder of mass `M` and radius `R`, about the axis of cylinder is
View SolutionState the expression for the moment of inertia of a solid cylinder of uniform cross section about an axis through its centre and perpendicular to its length.
View SolutionState the expression for the moment of inertia of a solid cylinder of uniform cross section about an axis through its centre and perpendicular to its length.
View SolutionWhat is moment of inertia of a solid sphere about its diameter ?
View SolutionA wheel of mass 8 kg and radius of gyration 25 cm is rotating at 300 rpm. What is its moment of inertia ?
View SolutionThree point masses `m_(1), m_(2)` and `m_(3)` are located at the vertices of an equilateral triangle of side `alpha`. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through `m_(1)?`
View SolutionThree balls of masses `1 kg, 2 kg and 3 kg` are arranged at the corners of an equilateral triangle of side `1 m`. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View SolutionFour particles of masses `4 kg, 2 kg, 3kg and 5 kg` are respectively located at the four corners `A, B, C, D` of a square of side `1 m`. Calculate the moment of inertia of the system about
(i) the axis passing through point of intersection of the diagonals and perpendicular to the plane of the square. (ii) side `AB` (ii) diagonal `BD`.
View SolutionFour particles of masses `4 kg, 2 kg, 3kg and 5 kg` are respectively located at the four corners `A, B, C, D` of a square of side `1 m`. Calculate the moment of inertia of the system about
(i) the axis passing through point of intersection of the diagonals and perpendicular to the plane of the square. (ii) side `AB` (ii) diagonal `BD`.
View SolutionFour particles of masses `4 kg, 2 kg, 3kg and 5 kg` are respectively located at the four corners `A, B, C, D` of a square of side `1 m`. Calculate the moment of inertia of the system about
(i) the axis passing through point of intersection of the diagonals and perpendicular to the plane of the square. (ii) side `AB` (ii) diagonal `BD`.
View SolutionCalculate the moment of inertia of a cylinder of length `1.5 m`, radius `0.05m` and density `8 xx 10^(3) kg//m^(3)` about the axis of the cylinder.
View SolutionCalculate the moment of inertia of the earth about its diameter, taking it to be a sphere of `10^(25)` kg and diameter 12800 km.
View SolutionFour spheres of diameter 2a and mass M are placed with their centres on the four corners of a square of side b. Then moment of inertia of the system about an axis about one of the sides of the square is :-
View SolutionTwo point masses of 2kg and 10 kg are connected by a weightless rod of length 1.2 m. Calculate the `M.I.` of the system about axis pasing through the centre of mass and perpendicular to this system.
View SolutionFind the moment of inertia of a rectangular bar magnet about an axis passing through its centre and parallel to its thickness. Mass of magnet is `100 g`, its length is `12 cm`, breadth is `3 cm` and thickness is `2 cm`.
View SolutionCalculate the ration of radii of gyration of circular ring and a disc of the same radius about the axis passing through their centres and perpendicular to their planes.
View SolutionFind the radius of gyration of a hollow uniform sphere of radius `R` about its tangent.
View SolutionFind the radius of gyration and moment of inertia of a rod of mass `100g` and length `1 m` about an axis passing through its centre and perpendicular to its length.
View SolutionA wheel is rotating at a speed of 1000 rpm and its `KE is 10^(6) J`. What is moment of inertia of the wheel about its axis of rotation ?
View SolutionCalculate the `KE` of rotation of a circular disc of mass `1 kg` and radius `0.2 m` rotating about an axis passing through its centre and perpendicular to its plane. The disc is making `30//pi` rotations per minute.
View SolutionAn energy of `484 J` is spent in increasing the speed of a flywheel from 60 rpm to 360 rpm. Calculate moment of inertia of flywheel.
View SolutionCalculate rotational `K.E.` of earth about its own axis, taking it to be a sphere of mass `6 xx 10^(24) kg` and radius `6400 km`.
View SolutionA metre stick is held vertically with one end on the floor and is then allowed to fall . Find the speed of the other end when it hits the floor , assuming that the end of the floor does not slip . Take g = 10 m/`s^(2)`.
`[sqrt30 m//s]`
View SolutionA uniform circular disc of mass `m` is set rolling on a smooth horizontal table with a uniform linear velocity `v`. Find the total K.E. of the disc.
View SolutionA solid sphere is rolling on a frictionless plane surface about the axis of symmetry. Find the rotational energy of the sphere. Also, find the ratio of rotational `K.E.` to total energy.
View SolutionA wheel of mass `5 kg` and radius `0.40 m` is rolling on a road without sliding with angular velocity `10 rad s^-1`. The moment of ineria of the wheel about the axis of rotation is `0.65 kg m^2`. The percentage of kinetic energy of rotate in the total kinetic energy of the wheel is.
View SolutionA solid cylinder rolls down an inclined plane. Its mass is `2 kg and radius 0.1 m`. It the height of the inclined plane is `4m`, what is its rotational `K.E.` when it reaches foot of the plane ? Assume that the surfaces are smooth. Take `M.I.` of solid cylinder about its axis = `mr^(2)//2`.
View SolutionA bucket of mass `8 kg` is supported by a light rope wound around a solid wooden cylinder of mass `12 kg and radius 20 cm`, free to rotate about its axis. A man holding the free end of the rope with the bucket and the cylinder at rest initially, lets go the bucket freely downward in a well `50 m` deep. Neglecting friction, obtain the speed of bucket and angular speed of the cylinder just before the bucket enters water. Take `g = 10 m//s^(2)`.
View SolutionRelate torque with angular acceleration
View SolutionEstablish a relation between angular momentum and moment of inertia of a rigid body.
View SolutionA torque of `2.0 xx 10^(-4)` Nm is applied to produce an angular acceleration of `4 "rad s"^(-2)` in a rotating body. What is the moment of inertia of the body ?
View SolutionA car moves on a road with a speed of `54 km h^(-1)`. The radius of its wheels is `0.35 m`. What is the average negative torque transmitted by its brakes to the wheels if the car is brought to rest in `15 s`? Moment of inertia of the wheels about the axis of rotation is `3 kg m^(2)`.
View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. What force should be applied tangentially to the rim of the flywheel so that it acquires an angular acceleration of `2 "rad s"^(-2)` ?
View SolutionA torque of 10 Nm is applied to a flywheel of mass 10 kg and radius of gyration 50 cm. What is the resulting angular acceleration ?
View SolutionA grindstone has moment of inertia of `6 kg m^(2)`. A constant torque is applied and the grindstone is found to have a speed of `150` rpm, 10 second after satrting from rest. Calculate the torque.
View SolutionA flywheel of mass 25 kg has a radius of 0.2 m. It is making 240 r.p.m. what is the torque necessary to bring it to rest in 20 s ? If the torque is due to a force applied tangentially on the rim of the flywheel, what is the magnitude of the force ?
View SolutionA cord is wound around the circumference of a wheel of diameter 0.3 m. The axis of the wheel is horizontal. A mass of 0.5 kg is attached at the end of the cord and it is allowed to fall from rest. If the weight falls 1.5 m in 4s, what is the angular acceleration of the wheel ? Also find out the moment of inertia of the wheel.
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass `20 kg` and radius `20 cm`. A steady pull of `25 N` is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
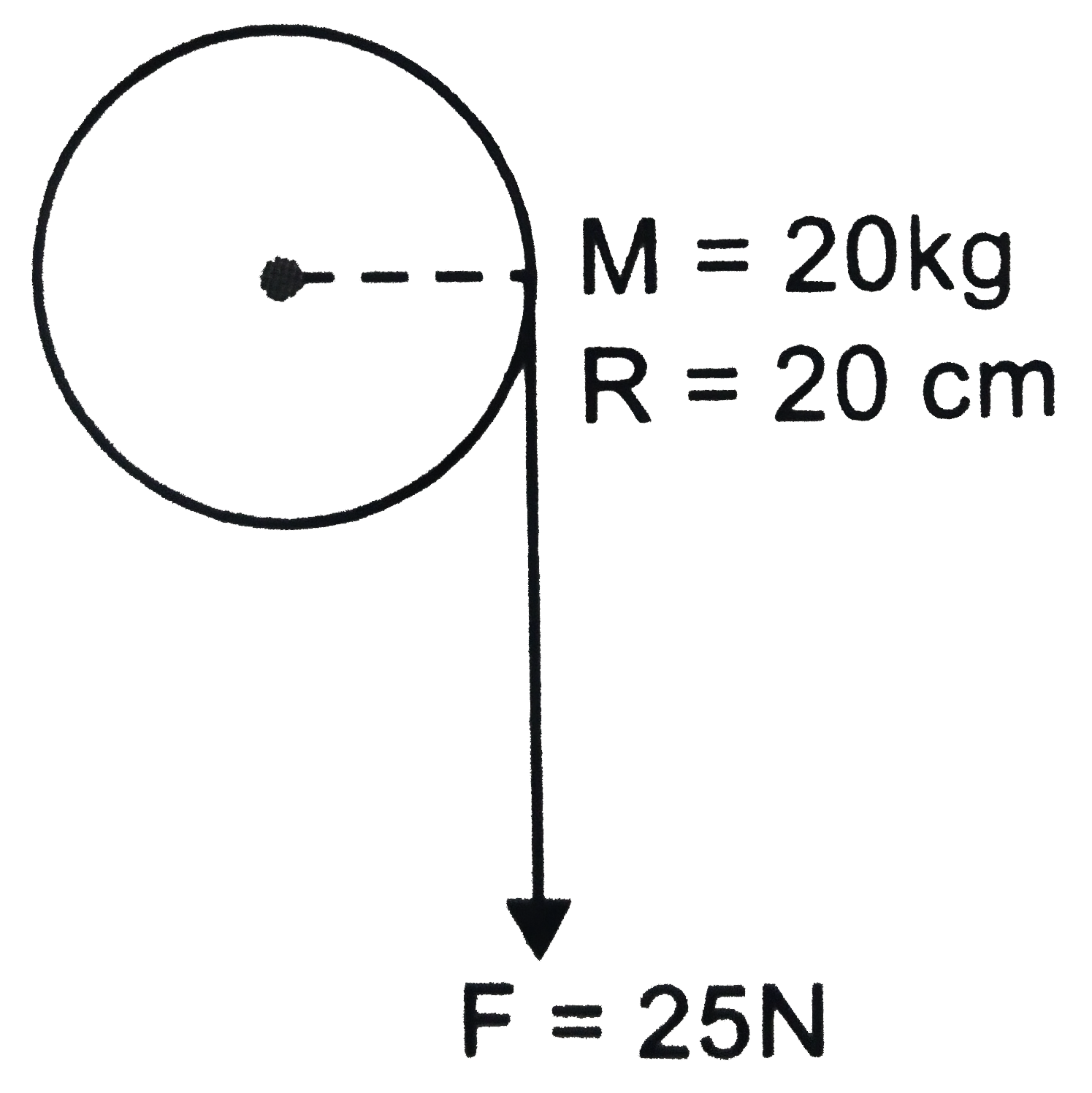
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when `2 m` of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass `20 kg` and radius `20 cm`. A steady pull of `25 N` is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
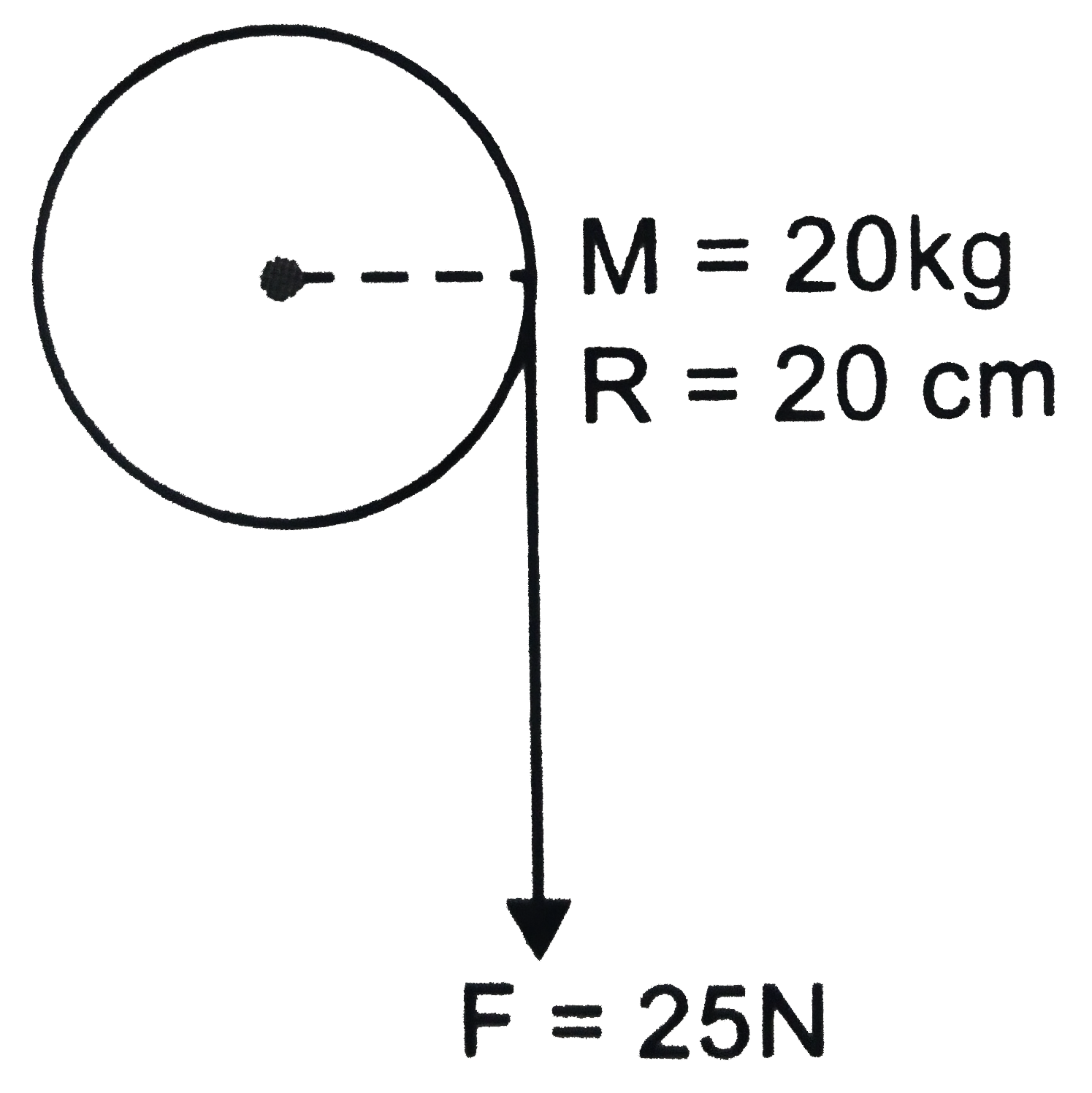
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when `2 m` of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass `20 kg` and radius `20 cm`. A steady pull of `25 N` is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
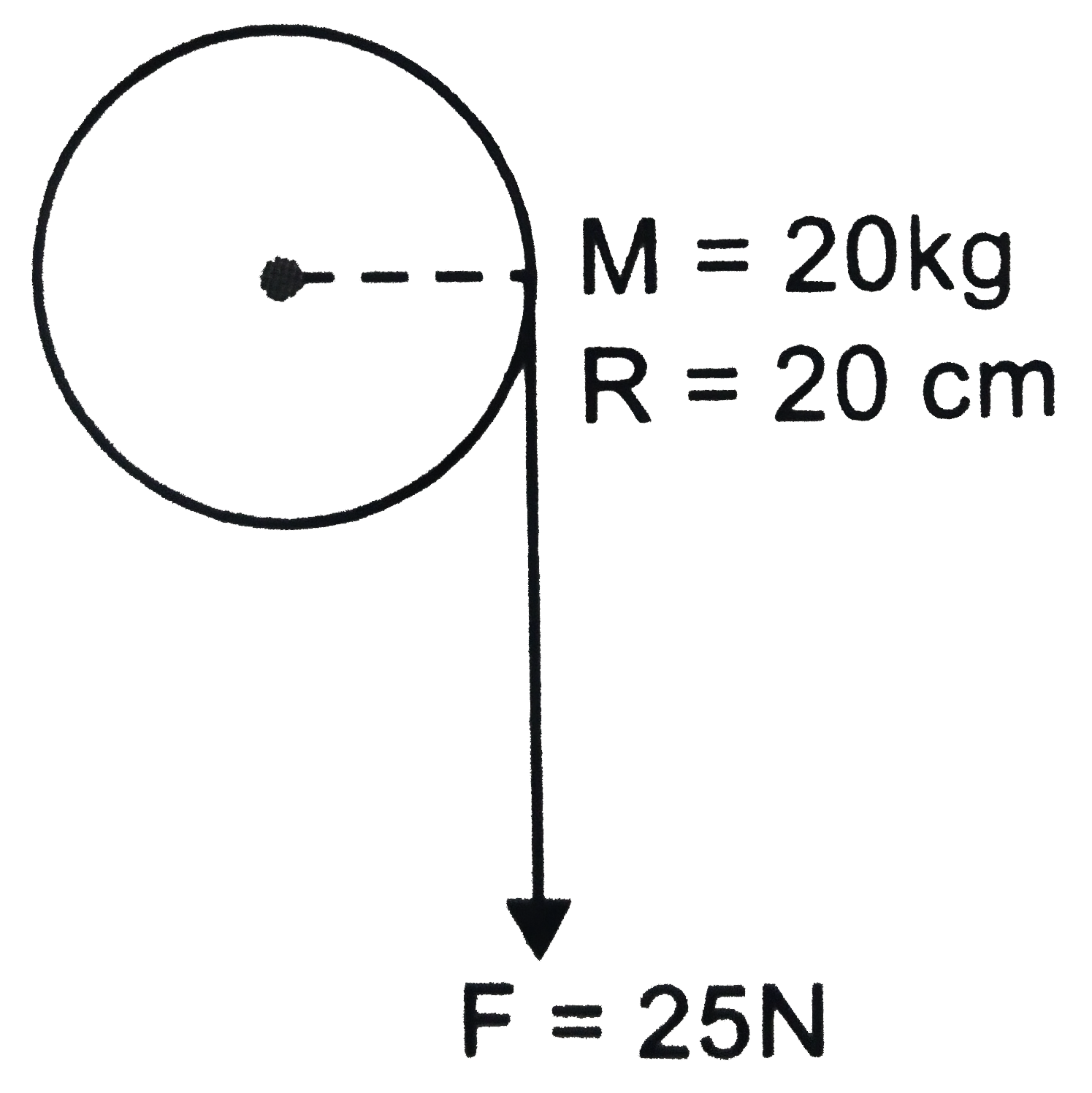
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when `2 m` of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View Solution
EXAMPLE questions and complete solutions for chapter System of particles & rotational Motion of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11