Complete Solutions to JEE Main And Advanced of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 54 |
| Academic Year | 2023-24 |
The numerical value of the angular velocity of rotation of the earth should be…….. Rad/s in order to make the effective acceleration due to gravity equal to zero.
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
View SolutionThe masses and radii of the Earth and the Moon are `M_1, R_1 and M_2,R_2` respectively. Their centres are at a distance d apart. The minimum speed with which a particel of mass m should be projected from a point midway between the two centres so as to escape to infinity is ........
View SolutionA particle is projected vertivally upwards from the surface of earth `(`radius` R_e)` with a kinetic energy equal to half of the minimum value needed for it to escape. The height to which it rises above the surface of earth is ……
View Solutionit possible to put an artifical1 satellite into orbit in such a way that it will always remain directly over New Delhi.
View SolutionIf the radius of the earth were to shrink by one percent its mass remaining the same, the acceleration due to greavity on the earth's surface would
View SolutionIf g is the acceleration due to gravity on the earth's surface, the gain in the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth, is
View SolutionIf the distance between the earth and the sun were half its present value, the number of days in a year would have been
View SolutionA geo-stationary stellite orbits around the earth in a circular orbit of radius 36,000km. Then, the time period of a spy stellite orbitting a few hundred km above the earth's surface `(R_(earth) = 6400km)` will approximately be
View SolutionA simple pendulum is oscillating without damiping, When the displacement of the bob is less than maximum, its acceleration vector `veca` is correctly show in:
View SolutionA binary star system consists of two stars A and B which have time period `T_A and T_B, radius R_Ba` and mass `M_a and M_B.` Then
View SolutionA spherically symmetric gravitational system of particles has a mass density` rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):}` where`rho_0` is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce `r(0ltrltOO)` form the centre of the system is represented by
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

View SolutionA satellite is moving with a constant speed 'V' in a circular orbit about the earth. An object of mass 'm' is ejected from the satellite such that it just escapes form the gravitational pull of the earth. At the tme of its ejection, the kinetic energy of the object is
View SolutionA planet of radius `R=(1)/(10)xx(radius of Earth)` has the same mass density as Earth. Scientists dig a well of depth`(R )/(5)` on it and lower a wire of the same length and a linear mass density `10^(-3) kg m(_1)` into it. If the wire is not touching anywhere, the force applied at the top of the wire by a person holding it inplace is (take the radius of Earth`=6xx10^6m` and the acceleration due to gravity on Earth is `10ms^(-2)`
View SolutionImagine a light planet revoling around a very massiv star in a circular orbit of radius R with a period of revolution T. if the gravitatinal force of attraction between the planet and the star is proportional to `R-(5//2)`
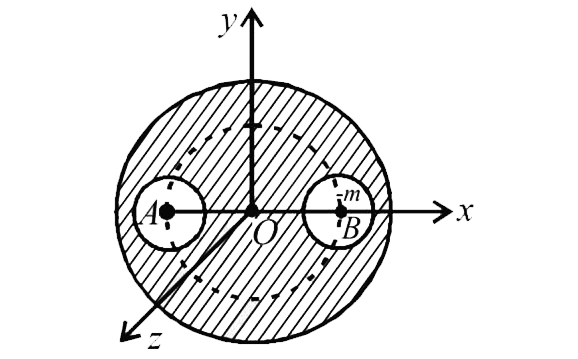
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionThe magnitude of the gravitational field at distance `r_1` and `r_2` from the centre of a unifrom sphere of radius R and mass m are `F_1 and F_2` respectively. Then:
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo spherical planets P and Q have the same uniform density `rho,` masses `M_p and M_Q` and surface areas A and 4A respectively. A spherical planet R also has uniform density `rho` and its mass is `(M_P + M_Q).` The escape velocities from the plantes P,Q and R are `V_P V_Q and V_R` respectively. Then
View SolutionTwo bodies, each of mass M, are kept fixed with a separation 2L. A particle of mass m is projected from the midpoint of the line joining their centres, perpendicular to the line. The gravitational constant is G. The correct statement (s) is (are)
View SolutionTwo satellites `S_1 and S_2` revole round a planet in coplanar circular orbits in the same sanse. Their periods of revolution are 1 hour and 8 hour respectively. The radius of the orbit of `S_1` is `10^4 km,` When `S_2` is closest to `S_1` find
(i) the speed of `S_2` relative to `S_1`
(ii) the angular speed of `S_2` as actually observed by an astronaut is `S_1.`
View SolutionThree particles, each of mass m, are situated at the vertices of equilateral triangle of side length a. The only forces. It is desired that each particle moves in a circle while maintaining the original mutual speration a. Find the intial velocity that should be given to each particle and also the time period of the circular motion.
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above the earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.
View SolutionThe distance between the centres of two stars is `10alpha`. The masses of these stars are M and 16M and their radii `alpha ` and `2alpha`. A body of mass m is fired straight from the surface of the larger star towards the smaller star. What should be its minimum initial speed to reach the surface of teh smaller star? Obtain the expression interms of G, M and `alpha`.
View SolutionA body is projected vartically upwards from the bottom of a crater of moon of depth `( R)/(100)` where R is the radius of moon with a velocity equal to the escape velocity on the surface of moon. Calculate maximum height attained by the body formt eh surface of the moon.
View SolutionAssertion : An astronaut in an orbiting space station above the earth experience weightlessness.
Reason : An object moving around the earth under the infuence of earth's gravitational force is in a state of 'free fall'
View SolutionAssertion : An astronaut in an orbiting space station above the earth experience weightlessness.
Reason : An object moving around the earth under the infuence of earth's gravitational force is in a state of 'free fall'
View SolutionGraviational acceleration on the surface of plane fo `(sqrt6)/(11)g.` where g is the gracitational acceleration on the surface of the earth. The average mass density of the planet is `(2)/(3)` times that of the earth. If the escape speed on the surface of the earht is taken to be `11 kms^(-1)` the escape speed on teh surface of the planet in `kms^(-1)` will be
View SolutionA bullet is fired vertically upwards with velocity v form the surface of a spherical planet. If the escape velocity from the planet is `v_(esc) = vsqrtN`, then the value of N is (ignore energy loss due to atmosphere)
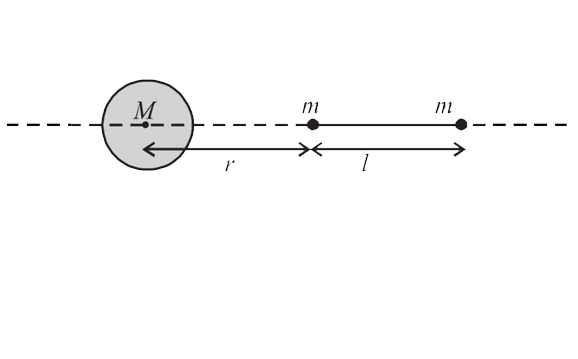
View SolutionA larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only throght their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tensin in the rod is zero for `m =k((M)/(288)).` The value of k is
View SolutionThe kinetic energy needed to project a body of mass m from the eath surface (radus R) to infinity is
View SolutionIf suddenly the gravitational force of attraction between Earth and a stellite revolving around it becomes zero, then the stellite will
View SolutionEnergy required to move a body of mass m from an orbit of radius 2R to 3R is
View SolutionThe escape velocity of a body depeds upon mass as
View SolutionThe time period of a satellite of earth is 5 hours. If the separation between the earth and the satellite is increased speartion between the earth and the satellite is increased to 4 times the previous value, the new time period will becomes
View SolutionTwo spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View SolutionThe escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of `45^@` with the vertical, the escape velocity will be
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View SolutionThe time period of an earth stellite in circuarl orbit is independet fo
View SolutionIf 'g' is the potential energy of an object of mass 'm' raised from the surface of the earth to a height equal to the radius 'R' of the earth is
View SolutionSuppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius 'R' around the sun will be proportional to
View SolutionThe change in the value of 'g' at a height 'h' above the surface of the earth is the same as at a depth 'd' below the surface of earth. When both 'd' and 'h' are much smaller then the radius of earth, then which one of the following is correct?
View SolutionA particle of mass 10g is kept on the surface of a uniform sphere of masss 100kg and radius 10cm. Find the work to be done against the gravitational force between them to take the particel far away from the sphere (you may take `G = 6.67xx10^(-11) Nm^2 /kg^2)`
View SolutionAverage density of the earth
View SolutionA planet in a distant solar systyem is 10 times more massive than the earth and its radius is 10 times smaller. Given that the escape velocity from the earth is `11kms^(-1)`, the escape velocity from the surface of the planet would be
View SolutionThis question contains Statement -1 and Stantement -2 Of the four choices given after the statements, choose the one that best desctibes the two statemesnts.
Statement -1:
For a mass M kept at the center of a cube of side 'a', the flux of gravitational field passing through its sides `4piGM.`
Statement -2:
If the direction of a field due to a point source is radial and its dependence on the distance 'r' from the source is given as `(1)/(r^2)`, its flux throught a closed surface depends only on the strength of the source enclosed by the surfcae and not on the size or shape of the surface.
View SolutionThe height at which the acceleration due to gravity becomes `(g)/(9)` (where g =the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is :
View SolutionTwo bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is:
View SolutionThe mass of a spaceship is 1000kg. It is to be launched from the earth's surface out into free space. The value of g and R (radius of earth) are `10m/s^2` and 6400 km respectively. The required energy for this work will be:
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionFrom a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential `V =0at r = oo,` the potential at (G = gravitational constatn)

View SolutionA satellite is revolving in a circular orbit at a height 'h' from the earth's surface (radius of earth R, h ltltR). The minimum increase in its orbital velocity required, So that the satellite could escape from the erth's gravitational field, is close to :(Neglect the effect of atomsphere.)
View Solution
JEE Main And Advanced questions and complete solutions for chapter GRAVITATION of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11