Complete Solutions to JEE Main And Advanced of chapter WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVES |
| SUNIL BATRA | JEE Main And Advanced |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A travelling wave has the frequency `v` and the particle displacement amplitude `A`. For the wave the particle velocity amplitude is ………………… and the particle acceleration amplitude is ……………………..
View SolutionSound waves of frequency `660 Hz` fal normally on a perfectly reflecting wall. The shortest distance from the wall at which the pair particles have maximum amplitude of vibration is ……………… meters.
View SolutionTwo simple harmonic motions are represented by the equations
`y_(1) = 10 sin(3pit + pi//4) and y_(2) = 5(sin 3pit + sqrt(3)cos 3pit)` their amplitude are in the ratio of ………… .
View SolutionIn a sonometer wire, the tension is maintained by suspending a `50 kg` mass from the free end of the wire. The suspended mass is completely submerged in water, the fundamental frequency will become …………… `Hz`.
View SolutionThe displacement of a wave disturbance propagating in the positive x-direction is given by
`y =(1)/(1 + x^(2))`at `t = 0` and `y =(1)/(1 +(x - 1)^(2))` at `t =2s`
where, `x` and `y` are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionA cylinder resonance tube open at both enda has fundamental frequency `F` in air. Half of the length of the tube is dipped vertically in water. The fundamental frequency to the air culumn now is …………………… .
View SolutionA bus is moving towards a gauge wall with a velocity of `5m//s^(-1)`. The driver sounds a horn of frequency `200 Hz`. The frequency of the beats heard by a passenger of the bus will be ………… `Hz` (Speed of sound in air `= 342m//s^(-1))`
View SolutionA main stands on the ground at a fixed distance from a siren which emits sound of fixed amplitude. The man hears the sound to be on a clear night than on a clear day.
View SolutionA plane wave of sound travelling in air is incident upon a plane water surface. The angle of incidence is `60@`. Assuming sneill's law to be valid for sound waves, it follows that the sound wave will be refrected into water away from the normal.
View SolutionA source of sound with frequency `256 Hz` is moving with a velocity `V` towards a wall and an observer is stationary detween the source and the wall. When the observer is between the source and the wall he will hear beats.
View SolutionA cylindrical tube open at both ends, has a fundamental frequency '`f` in air. The tube is dipped vertically in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column in now
View SolutionA wave representing by the equation `y = a cos(kx - omegat)` is superposed with another wave to form a stationary wave such that `x = 0` is a node. The equation for the other wave is
View SolutionAn object of specific gravity `rho` is hung from a thin steel wire. The fundamental frequency for transverse standing waves in wire is `300 Hz`. The object is immersed in water so that one half of its volume is submerged. The new fundamental in `Hz` is
View SolutionA wave disturbance in a medium is described by `y(x, t) = 0.02 cos((50pit + (pi)/(2))cos(10pix)` where `x and y` are in meter and `t` is in second`
View SolutionThe extension in a string, obeying Hooke's law, is x. The speed of sound in the stretched string is v. If the extension in the string is increased to `1.5 x`, the speed of sound will be :-
View SolutionAn open pipe is suddenly closed at one end with the result that the frequency of third harmonic of the closed pipe is found to be higher by `100 Hz` then the fundamental frequency of the open pipe. The fundamental frequency of the open pipe is
View SolutionA travelling wave in a stretched string is described by the equation `y = A sin (kx - omegat)` the maximum particle velocity is
View SolutionA train moves towards a stationary observer with speed `34 m//s`. The train sounds a whistle and its frequency registered by the obsrever is `f_(1)`. If the train's speed is reduced to `17 m//s`, the freuqncy registered is `f_(2)`. If the speed of sound of `340 m//s`, then the ratio `f_(1)//f_(2)`is
View SolutionTwo vibrating strings of the same material but lengths `L` and `2L` have radii `2r` and `r` respectively. They are stretched under the same tension. Both the string vibrate in their fundamental nodes, the one of length `L` with freuqency `v_(1)` and the other with frequency `v_(2). the raio `v_(1)//v_(2)` is given by
View SolutionTwo monatomic ideal gases `1` and `2` of molecular masses `m_(1)` and `m_(2)` repectively are enclosed in separate containers kept at the same temprature. The ratio of the of sound in gas `1` to that in gas `2` is given by
View SolutionTwo pulse in a stretched string whose centers are initially `8cm` apart are moving towards each other as shown in the figure. The speed of each pulse is `2cm//s`. After `2seconds`, the total energy of the pulse will be
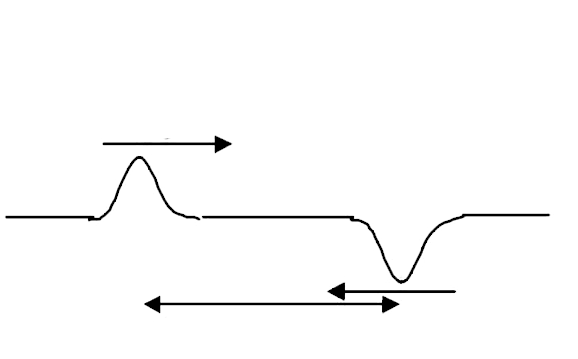
View SolutionThe ends of a stretched wire of length `L` are fixed at `x = 0 and x = L`. In one experiment, the displacement of the wire is `y_(1) = A sin(pi//L) sin omegat` and energy is `E_(1)` and in another experiment its displacement is `y_(2) = A sin (2pix//L ) sin 2omegat` and energy is `E_(2)`. Then
View SolutionA siren placed at a railway platform is emmitting sound of frequency `5 kHz`. A passenger sitting in a moving train `A` records a frequency of `5.5kHz` while the train approaches the siren. During his return journey in a different train `B` he records a frequency of `6.0 kHz` while approaching the same siren. the ratio the velocity of train of `A` is
View SolutionA sonometer wire resonates with a given tuning fork forming standing waves with five antitodes between the two bridges when a mass of `9kg` is suspended from the wire. when this same tuning fork forming three antitodes for the same positions of the bridges. the value of `M` is
View SolutionA police car moving at `22m//s`, chases motorcyclist. The police man sounds his horn at `176 Hz`, while both of them move towards a ststionary siren of frequency `165 Hz`. Calculate the speed of the motorcycle, if it is given that he does not observes any beats.

View SolutionIn the eperiment for the determinetion of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fundamental mode, with a tuning fork is `0.1m`. When this length is changed to `0.35m`, the same tuning fork resonates with the first overone. calculate the end correction.
View SolutionA pipe of length `l_(1)`, closed at one end is kept in a chamber of gas of density `rho_(1)`. A second pipe open at both ends is placed in a second chamber of gas of density `rho_(2)`. The compressibility of both the gases is equal. Calculate the length of the second pipe if frquency of first overtone in both the cases is equal
View SolutionIn a resonance tube with tuning fork of frequency `512 Hz`, first resonance occurs at water level equal to `30.3cm` and second resonance ocuurs at `63.7cm`. The maximum possible error in the speed of sound is
View SolutionAn open pipe is in resonance in `2nd` harmonic with frequency `f_(1)`. Now one end of the tube is closed and frequency is increased to `f_(2)` such that the resonance again ocuurs in `nth` harmonic. Choose the corrct option
View SolutionA massless rod of length `L` is suspened by two identical string `AB` and `CD` of equal length. A block of mass `m` is suspended from point `O` such that `BO` is equal ti 'x'. Further it is obsreved that the frequency of `1st` harmonic in `AB` is equal to `2nd` harmonic frequency in `CD`. 'x' is
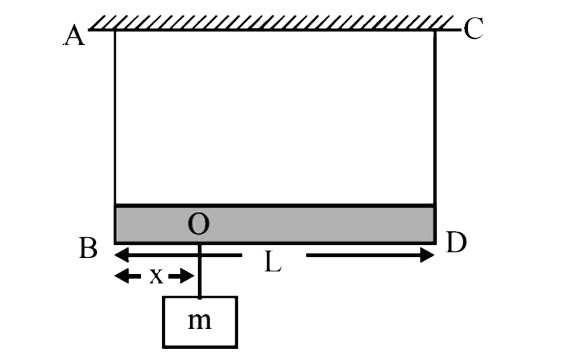
View SolutionIn the experiment to determine the speed of sound using a resonance column,
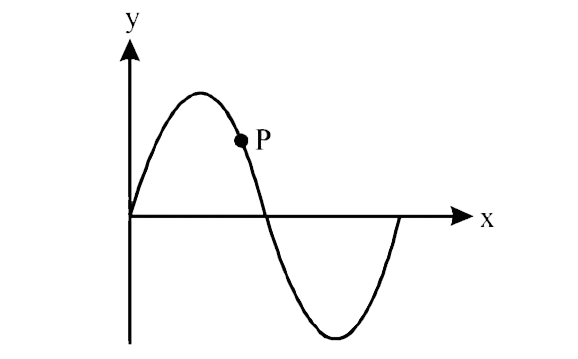
View SolutionA transverse sinusoidal wave moves along a string in the positive x-direction at a speed of `10cm//s`. The wavelength of ythe wave is `0.5m` and its amplitude is `10cm`. At a particular time `t`, the snap-shot of the wave is shown in figure. The velocity of point `P` when its displacement is `5cm` is -
View SolutionA vibrating string of certain length `l` under a tension `T` resonates with a maode corresponding to the first overtone (third harmonic) of an air column of length `75cm` inside a tube closed at one end. The string also gereates `4` beats per second when excited along with a tuning fork of frequency `n`. now when the tension of the string is slightly increased the number of beats reduces `2` per second. assuming the velocity of sound in air ti be `340 m//s`, the frequency `n` of the tuning fork in `Hz` is
View SolutionA hollow pipe of length `0.8m` is closed at one end. At its open end a `0.5 m` long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is `50 N` and the speed of sound is `320 ms^(-1)`, the mass of the string is
View SolutionA police car with a siren of frequency `8 KHz` is moving with uniform velocity `36 Km//hr` towards a ball building which reflects the sound waves. The speed of sound in air is `320 m//s`. The frequency of the siren heard by the car driver is
View SolutionA student is performing the experiment of resonance column. The diameter of the column tube is `4cm`. The frequency of the tuning fork is `512 Hz`. The air tempreture is `38@C` in which the speed of sound is `336 m//s`. The zero of the meter scale coincide with the top end of the resonance column tube. when the first resonance ocuurs, the reading of the water level in the column is
View SolutionA wave equation which gives the displacement along the y-direction is given by `y = 10^(-4) sin(60t + 2x)` where `x and y` are in meters and `t` is time in secinds. This represents a wave
View SolutionA travelling wave is described by the equation `y = y_(0) sin ((ft - (x)/lambda))`. The maximum particle velocity is equal to four times the wave velocity if
View SolutionAn air columbn in pipe, which is closed at one end, will be in resonance with a vibrating tuning fork of frequency `264 Hz` if the length of the column in `cm` is :
View SolutionA tube, closed at one end and containing air, produces, when excited, the fundamental note of frequency `512 Hz`. If the tube is open at both ands the fundamental frequency that can be excited is (in Hz)
View SolutionThe displacement of partcles in a string streched in the x-direction is by `y`. Among the following expressions for `y`, those describing wave motion are :
View SolutionAn organ pipe `P_(1)` open at one end vibrating in its first harmonicare and another pipe `P_(2)` open at ends vibrating in its third harmonic are in resonance with a given tuning fork. The ratio of the length of `P_(1)` to that `P_(2)` is
View Solutionvelocity of sound in air is `320m//s`. A pipe closed at one end has of `1m`. Negative end corrections, the air column in air pipe can resonate for sound of frequency :
View SolutionA wave is represented by the equation
`y = A sin(10pix + 15pit + (pi)/(3))`
where `x` is in meter and `t` is in seconds. The expression represents :
View SolutionTwo idential straight wires are stretched so as to produce `6` beats per second when vibrating simultaneously. On changing the tension slightly in one of them, the beat frequency remains unchanged. Denoting by `T_(1)`, `T_(2)` the higher and the lower initial tension in the strings, then it could be said that while making the above changes in tension,
View SolutionThe displacement `y` of a particle executing periodic motion is given by `y = 4 cos^(2) ((1)/(2)t) sin(1000t)`
This expression may be considered to be a result of the superposition of
View SolutionA sound wave of frequency `f` travels horizontally to the right. It is reflected from a large vertical plane surface moving to left with a speed `v`. The speed of sound in mwdium is `C`
View SolutionA string of length `0.4 m` and mass `10^(-2)kg` is tightly clamped at its ends. The tension in the dtring is `1.6 N`. Idential wave pulse are produced at one end at equal intervals of time, `Deltat`. The minimum value of `Deltat` which allows constructive inetrference successive pulse is
View SolutionThe `(x, y)` co-ordinates of the corners of a square plate are `(0, 0)`, `(L, L)` and `(0, L)`. The edges of the plate are clamped and transverse standing waves are set up in it. If `u(x, y)` denotes the displacement of the plate at the point `(x, y)` at some instant of time, the possible expression `(s)` for `u` is (are) (a = posotive constant)
View SolutionA transverse sinusoidal wave of amplitude a, wavelength `lambda` and frequency `f` is travelling on a stretched string. The maximum speed of any point in the string is `v//10`, where `v` is the speed of propagation if the wave. If `a = 10^(-3)m` and `v = 10ms^(-1)`, then `lanbda` and `f` are given by
View Solution`y(x, t) = 0.8//[4x + 5t)^(2) + 5]` represents a moving pulse, where `x` and `y` are in meter and `t` in second. Then
View SolutionIn a wave motion `y = a sin (kx - omegat)`, `y` can represent
View SolutionStanding waves can be produced
View SolutionAs a wave propagates,
View SolutionA student performed the experiment to measured the speed of sound in air using resonance air-column method. Two resonances in the air-column were obtained by lowering the water level. The resonance with the shoter air-column is the first resinance and that with the longer air-column is the second resonance. then,
View SolutionA person blows into open- end of a long pipe. As a result, a high pressure pulse of air travel down the pipe. When this pulse reaches the other end of the pipe,
View SolutionA horizontal stretched string, fixed at two ends, is vibrating in its fifth harmonic according to the equation, `t(x, t) = (0.01m) sin[(62.8m^(-1))t]`. Assuming `pi = 3.14`, the correct statement `(s)` is (are)
View SolutionTwo vehicles, each moving with speed `u` on the same horizontal straight road, are spproaching each other. Wind blows along the road with velocity `w`. One of these vehicles blows a whistle of frequency `f_(1)`. An observer in the other vehicle hears the frequency of the whistle to be `f_(2)`. the speed of sond in still air is `VC`. the correct statement `(s)`is (are)
View SolutionA student is performing an experiment using a resonance column and a tuning fork of frequency `244s^(1-)`. He is told that the air in the tube has been replaced by another gas (assuming that the air column ramains filled with the gas). If the minimum height at which resonace occurs is `(0.350+- 0.005)m`, the gas in the tube is (Useful information : `sqrt(167RT) = 640J^(1//2)mode^(-1//2)`,
`sqrt(140RT) = 590J^(-1//2)`. the molar masses `M` in grams are given in the options. take the values of `sqrt((10)/(M))` for each gas as given there.)
View SolutionOne end of a taut string of length `3m` along the x-axis is fixed at `x = 0`. The speed of the waves in the string is `100ms^(-1)`. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength`(s)` of these sationary waves is (are)
View SolutionTwo loudspeaker `M` and `N` are located `20m` apart and emit sound at frequencies `118Hz` and `121Hz`, respectively. A car is intially at a point `P`, `1800m` away from the midpoint `Q` of the line `MN` and moves towards `Q` constantly at `60 km//hr` along the perpedicular bisector of `MN`. it crosses `Q` and eventually reaches a point `R`, `1800m` away from `Q`. let `v(t)` represent the beat frequency measured by a person sitting in the car at time `t`. let `v_(P)`, `v_(Q) and v_(R)` be the beat frequencies measured at locations `P`,`Q` and `R`, respectively. the speed of sound in air is `330ms^(-1)`. which of the following statement (s) is (are) true regarding the sound heard by the person?
View Solution`AB` is a ccylinder of length `1m` fitted with a thin flexible diaphragn `C` at the middle and other thin flexible diaphragms `A` and `B` at the ends. The portions `AC` and `BC` contain hydrogen and oxygen gases respectively. The diaphragms `A` and `B` are set into vibrations of same frequency. what is the minimum frequency of these vibrations for which diaphragms `C` is a node? (Under the conditions of experiment `v_(H_(2) = 1100m//s`, v_(0_(2) = 300m//s`).

View SolutionA copper wire is held at the two ends by rigid supports. At `30^(@)C`, the wire is just taut, with negligible tension. Find the speed of transverse waves in this wire at `10^(@)C`.
Given : Young modulus of copper `= 1.3 xx 10^(11) N//m^(2)`.
Coefficient of linear expansion of copper ` = 1.7 xx 10^(-5) ^(@)C^(-1)`. Density of copper `= 9 xx 10^(3) kg //m^(3)`.
View SolutionA tube of a certain diameter and of length `48cm` is open at both ends. Its fundamental frequency is found to be `320 Hz`. The velocity of sound in air is `320 m//sec`. Estimate the diameter of the tube.
One end of the tube is now closed. Calculate the lowest frequrncy of resonance for the tube.
View SolutionA source of sound of frequency `256Hz` is moving rapidly towards wall with a velocity of `5m//sec`. How many beats per second will be heard if sound travels at a speed of `330m//sec`.
View SolutionA string `25cm` long and having a mass of `2.5 gm` is under tension. A pipe closed at one end is `40cm` long. When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, `8` beats per second are heard. It is observed that decreasing the tension in the string decreases beat frequency. if the speed of sound in air is `320m//s`, find the tension in the string.
View SolutionA uniform rope of length `12m` and mass `6kg` hangs vertically from a rigid support. A block of mass `2kg` is attached to the free end of the rope. A transverse pulse of wavelength `0.06m` is produced at the lower end of the rope. What is the wavelength of the pulse whwn it reaches the top of the rope?
View SolutionA steel wire of length `1m`, `mass 0.1kg` and uniform cross-sectional area `10^(-6)m^(2)` is rigidly fixed at both ends. The temperature of the wire is lowered by `20^(@)C`. If transverse calculate the frequency of the fundamental mode of vibration.
Given for steel `Y = 2 xx 10^(11)N//m^(2)`
`alpha = 1.21 xx 10^(-5) per ^(@)C`
View SolutionThe vibrations of a string of length `60cm` fixed at both ends are represented by the equation----------------------------
`y = 4 sin ((pix)/(15)) cos (96 pit)`
Where `x` and `y` are in `cm` and `t` in seconds.
(i) What is the maximum displacement of a point at `x = 5cm`?
(ii) Where are the nodes located along the string?
(iii) What is the velocity of the particle at `x = 7.5 cm` at `t = 0.25 sec`.?
(iv) Write down the equations of the component waves whose superpositions gives the above wave
View SolutionTwo tuning forks with natural frequencies of `340 Hz` each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency `3 Hz`. Find the speed of the tuning fork.
View SolutionThe following equations represent transverse waves :
`z_(1) = A cos(kx - omegat)`,
`z_(2) = A cos (kx + omegat)`, `z_(3) = A cos (ky - omegat)`
Identify the combineation (s) of the waves which will produce (i) standing wave(s), (ii) awave travelling in the direction making an angle of `45^(@)` degrees with the positive `x` and positive `y` axes. In each case, find the positions at which the resultant is always zero.
View SolutionA train approaching a hill at a speed of `40 km//hr` sounds a whistle of frequency `580 Hz` when it is at a distance of `1km` from a hill. A wind with a speed of `40km//hr` is blowing in the direction of motion of the train Find
(i) the frequency of the whistle as heard by an observer on the hill,
(ii) the distance from the hill at which the echo from the hill is heard by the driver and its frequency.
(Velocity of sound in air `= 1, 200 km//hr`)
View SolutionA source of sound is moving along a circular orbit of radius `3 meter` with an angular velocity of `10 rad//s`. A sound detector located far away from the source is executing linear simple harmonic motion along the line `BD` with an amplitude `BC = CD = 6 meters`. the frequency of oscillation of the detector is `(5)/(pi)` per second. the source is at the point `A` when the detector is at the point `B`. if the source emits a continous sound wave of frequency `340 Hz`, find the maximum and the mnimum frequencies recorded by the detector.

View SolutionThe displacement of the medium in a sound wave is given by the equation `y_(1) = A cos(ax + bt)` where `A`, `a and b` are positive constants. The wave is reflected by an obstacle situated at `x = 0`. The intensity of the reflected wave is `0.64` times that of the incident wave.
(a) What are the wavelength and ffrequency of incident wave?
(b) Write the equation for the reflected wave.
( c ) In the resultant wave formed after reflection, find the maximum and minimum values of the particle speeds in the medium.
(d) Express the resultant wave as a superposition of a standing wave and a travelling wave. what are the positions of the antinodes of the standing wave ? What is the direction of propagation of travelling wave?
View SolutionTwo radio stations broadcast their programmes at the same amplitude `A` and at slightly different frequencies `omega_(1)` and `omega_(2)` respectively, where `omega_(1) - omega_(2) = 10^(3) Hz A` detector receives the signals from the two stations simultaneously. it can only detect signals of intensity `ge 2A^(2)`.
(i) Find the time interval between successive maxima of the intensity of the signal received by the detector.
(ii) Find the time for which the detector remains idle in each cycle of the intensity of the signal.
View SolutionA whistle emmitting a sound of frequency `440 Hz` is tied to a string of `1.5m` length and rotated with an angular velocity of `20rad s^(-1) in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a large distance from the whistle.
View SolutionA band playing music at a frequency `f` is moving towards a wall at a speed `v_(b)`. A motorist is following the band with a speed `v_(m)`. If the speed of sound, obtain an expression for the beat frequency heard by the motorist.
View SolutionThe air column in a pipe closed at one end is made to vibrate in its second overtone by a tuning fork of frequency `440 Hz`. The speed of sound in air is `330ms^(-1)`. End corrections may be naglected. Let `P_(0)` denote the mean pressure at any point in the pipe, and `DeltaP` the maximum amplitude of pressure variation.
(a) Find the length `L` of the air column.
(b) What is the amplitude of pressure variation at the middle of the column?
( c ) What are the maximum and minimum pressures at the open end of the pipe?
(d) What are the maximum and minimum pressures at the closed end of the pipe?
View SolutionA long wire `PQR` is made by joining two wires `PQ` and `QR` of equal radii `PQ` has length `4.8 m` and mass `0.06 kg`. `QR` has length `2.56m` and mass `0.2 kg`. The wire `PQR` is under a tension of `80N`. A sinusoidal wave-pulse of amplitude `3.5cm` is sent along the wire `PQ` from end `P`. No power is dissipated during the propagation of the wave-pulse. caculate,
(a) the time taken by the wave-pulse to reach the other end `R` of the wire, and
(b) the amplitude of the reflected and transmitted wave-pulse after the incident wave-pulse crosses the jjoint `Q`.
View SolutionA `3.6m` long vertical pipe resonates with a source of frequency `212.5 Hz` when water level is at certain height in the pipe. Find the height of water level (from the bottom of the pipe) at which resonance occurs. Neglect end correction. Now , the pipe is filled to a height `H (~~ 3.6m)`. A small hole is drilled very close to its bottom and water is allowed to leak. Obtain an expression for the rate of fall of water level in the pipe as a function of `H`. If the radii of the pipe and the hole are `2 xx 10^(-2)m` and `1 xx 10^(-3)m` respectively, calculate the time interval between the occurance of first two resonances. Speed of sound in air `340m//s` and `g = 10m//s^(2)`.
View SolutionA boat is travelling in a river with a speed `2m//s`. From this boat, a sound transmitter is lowered into the river through a rigid support. The wavelength of the sound emitted from the transmitter inside the water is `14.45mm`. Assume that attenuation of sound in water and air is negligible.
(a) What will be the frequency detected by a receiver kept inside the river downstream?
(b) The transmitter and the receiver are now pulled up into air. the air is blowing with a speed `5m//s` in the direction opposite the river stream. Determine the frequency of the sound detected by the receiver.
Temperature of the air and water = `20^(@)C`, Density of river water `= 10^(3) kg//m^(3)`,
Bulk modulus of the water `= 2.088 xx 10^(9)`Pa, gas constant `R = 8.31 J//mol-K`,
Mean molecular mass of air `= 28.8 xx 10^(-3) kg//mol`, `C_(P)//C_(V)` for air `= 1.4`)
View SolutionTwo narrow cylindrical pipes `A and B` have the same length. Pipe `A` is open at both ends and is filled with a monoatomic gas of molar mass `M_(A)`. Pipe `B` is open at one end and closed at the other end, and is filled with a distomic gas of molar mass `M_(B)`. Both gases are at the same tempreture.
(a) If the frequency of the second harmonic of the fundamental mode in pipe `A` is equal to the frequency of the third harmonic of the fundamental mode in pipe `B`, determine the value of `M_(B)//M_(B)`.
(b) Now the open end of pipe `B` is also closed (so that the pipe is closed at both ends). Find the ratio of the fundamental frequency in pipe `A` to that in pipe `B`.
View SolutionA tuning fork of frequency `480 Hz` resonates with a tube closed at one end of length `16 cm` and diameter `5cm` in fundamental mode. Calculate velocity of sound in air.
View SolutionA string tied between `x = 0 and x = l` vibrates in fundamental mode. The amplitude `A`, tension `T` and mass per unit length `mu` is given. Find the total energy of the string.

View SolutionA whistling train approaches a junction. An observer standing at juction obsrever the frequency to be `2.2 KHz` and `1.8 KHz` of the approaching and the receding train respectively. Find the speed of the train (speed of sound `300m//s`)
View SolutionA transverse harmonic disturbance is produced in a string. The maximum transverse velocity is `3m//s` and maximum transverse acceleration is `9om//s`. If the wave velocity is `20 m//s` then find the waveform.
View SolutionWaves `y_(1) = Acos(0.5pix - 100pit)` and `y_(2)Acos(0.46pix - 92pit)` are travelling along x-axis. (Here `x` is in `m` and `t` is in second)
Find the number of times intensity is maximum in time interval of `1 sec`.
View SolutionWaves `y_(1) = Acos(0.5pix - 100pit)` and `y_(2)Acos(0.46pix - 92pit)` are travelling along x-axis. (Here `x` is in `m` and `t` is in second)
The wave velocity of louder sound is
View SolutionWaves `y_(1) = Acos(0.5pix - 100pit)` and `y_(2)Acos(0.46pix - 92pit)` are travelling along x-axis. (Here `x` is in `m` and `t` is in second)
The number of times `y_(1) + y_(2) = 0` at `x = 0` in `1sec` is
View Solutiontwo trains `Aand B` moving with speeds `20m//s` and `30m//s` respectively in the same direction on the same straight track, with `B` ahesd of `A`. The engines are at the front ends. The engine of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in the figure. the spread in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. the speed of sound in still air is `340 m//s`.
The speed of sound of the whistle is
View Solutiontwo trains `Aand B` moving with speeds `20m//s` and `30m//s` respectively in the same direction on the same straight track, with `B` ahesd of `A`. The engines are at the front ends. The engine of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in the figure. the spread in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. the speed of sound in still air is `340 m//s`.
The distribution of the sound intensity of the whistle as observed by the passengers in train `A` is best represented by
View Solutiontwo trains `Aand B` moving with speeds `20m//s` and `30m//s` respectively in the same direction on the same straight track, with `B` ahesd of `A`. The engines are at the front ends. The engine of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in the figure. the spread in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. the speed of sound in still air is `340 m//s`.
The spread of frequency as observed by the passenger in train `B` is
View SolutionA `20 cm` long string, having a mass of `1.0g`, is fixed at both the ends. The tension in the string is `0.5 N`. The string is into vibrations using an external vibrator of frequency `100 Hz`. Find the separation (in cm) between the successive nodes on the string.
View SolutionA stationary source is emmitting sound at a fixed frequency `f_(0)`, which is reflected by two cars approaching the source. The difference between the frequencies of sound reflected from the cars is `1.2%` of `f_(0)`. What is the difference in the speeds of the cars (in km per hour) to the nearest integer ? The cars are moving at constant speeds much smaller than the speed of sound which is `330 ms^(-1)`.
View SolutionWhen two progressive waves `y_(1) = 4 sin (2x - 6t)` and `y_(2) = 3 sin (2x - 6t - (pi)/(2))` are superimposed, the amplitude of the resultant wave is
View SolutionFour harmonic waves of equal freuencied and equal intensity `I_(0)` have phase angles `0, (pi)/(3), (2pi)/(3)` and `pi`. When they are superposed, the intensity of the resulting wave is `nI_(0)`. The value of `n` is
View SolutionLength of a string tied to two rigid support is `40cm`. Maximum length (wavelength in cm) of a stationary wave produced on it is
View SolutionTube `A` has both ends open while tube `B` has one closed, otherwise they are identical. The ratio of fundamental frequency of tube `A and B` is
View SolutionA tuning fork arrangement (pair) produces `4 beats//sec` with one fork of frequrncy `288cps`. A little wax is placed on the unknown fork and it then produces `2 beats//sec`. The frequency of the unknown fork is
View SolutionA wave `y = a sin (omegat - kx)` on a string meets with another wave producing a node at `x = 0`. Then the equation of the unknown wave is
View Solution
JEE Main And Advanced questions and complete solutions for chapter WAVES of SUNIL BATRA 41 YEARS IITJEE PHYSICS (HINGLISH) of Class 11