Complete Solutions to Assignement section -D (Linked Comprehension) of chapter MOTION IN A PLANE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A PLANE |
| AAKASH INSTITUTE | Assignement section -D (Linked Comprehension) |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
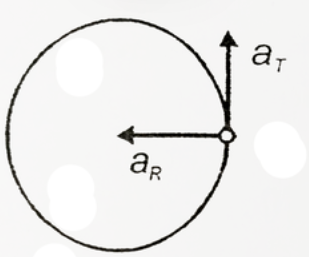
The time after which the speed of particle reduces to half of its initial value is
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
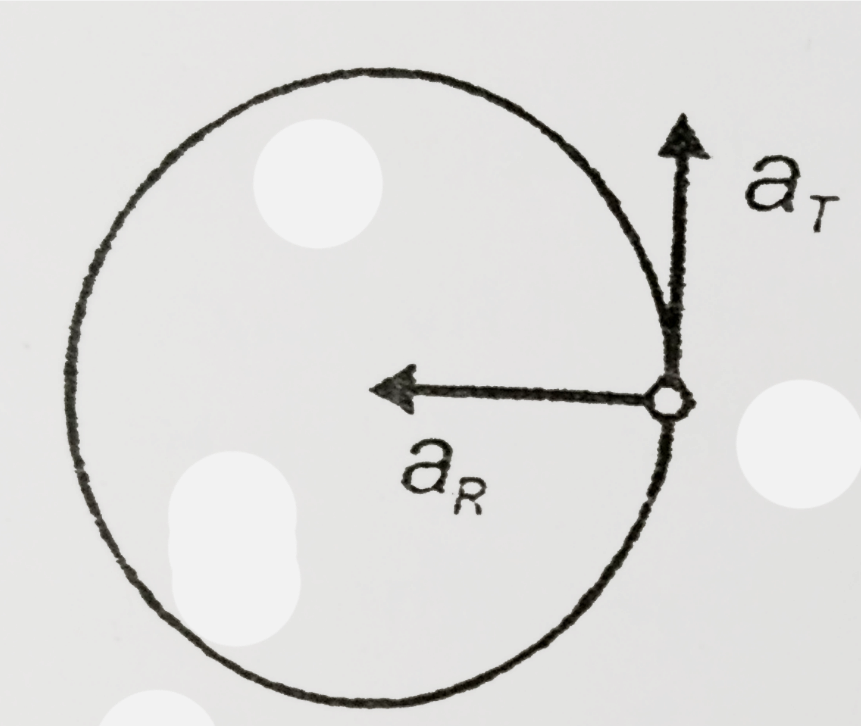
The magnitude of tangential acceleration at ` t = R/(2u)` is
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.

The magnitude of tangential acceleration at ` t = R/(2u)` is
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g `= 10 m//s^(2)]`
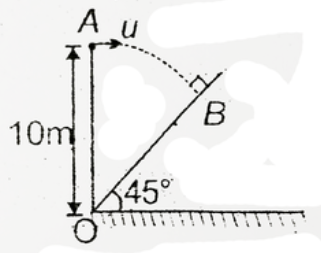
Find horizontal speed with which the particle was projected
View SolutionA particle is projected horizontally with spee u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g `= 10 m//s^(2)]`
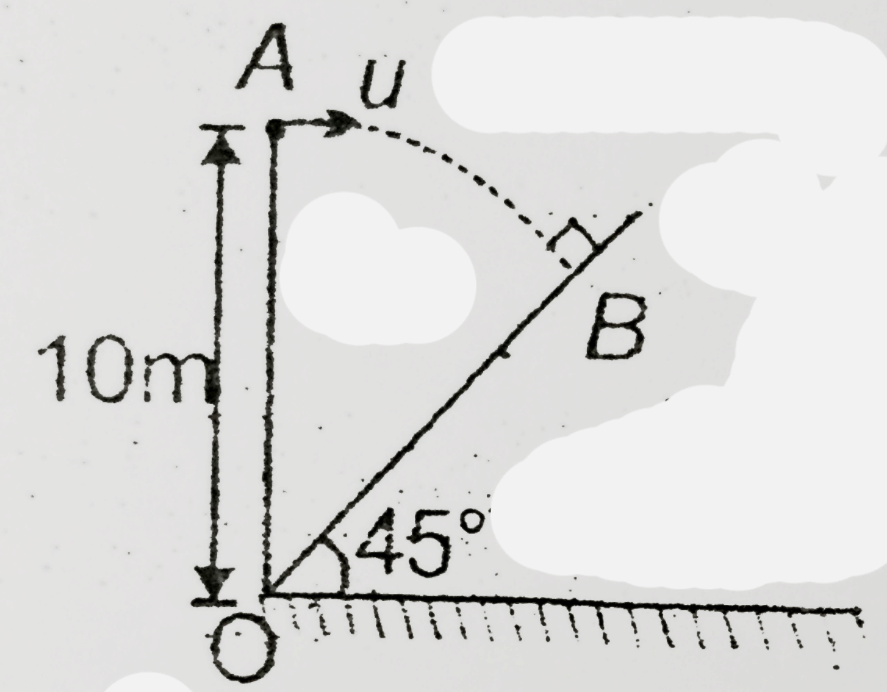
Find the length OB along the inclined plane
View SolutionA particle is projected horizontally with speed u from point A, which is 10 above the ground . If the particle hits the inclined perpendicularly at point B. [ g `= 10 m//s^(2)]`

Find horizontal speed with which the particle was projected
View SolutionWhen a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
After reversing its direction ,how much time was taken by the boat to meet the raft again ( i.e. `2^(nd)` time) ?
View SolutionWhen a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
Find the speed of river
View SolutionWhen a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
Now, it instead of 6 km they have met at 8 km from point P. Find the speed of river
View SolutionRaindrops are falling with velocity `10 sqrt2` m/s making and angle `45^(@)` with the vertical. The drops appear to be falling vertically to a man running with constant velocity . The velocity of rain drops change such that the rain drops now appear to be falling vertically with `sqrt3` times the velcoity it appeared earlier to the same person running with same velocity .
The magnitude of velocity of man w.r.t ground is
View SolutionRaindrops are falling with velocity `10 sqrt2` m/s making and angle `45^(@)` with the vertical. The drops appear to be falling vertically to a man running with constant velocity . The velocity of rain drops change such that the rain drops now appear to be falling vertically with `sqrt3` times the velcoity it appeared earlier to the same person running with same velocity .
After the velocity of rain drops change the magnitude of velocity of raindrops with respect to ground is
View SolutionRaindrops are falling with velocity `10 sqrt2` m/s making and angle `45^(@)` with the vertical. The drops appear to be falling vertically to a man running with constant velocity . The velocity of rain drops change such that the rain drops now appear to be falling vertically with `sqrt3` times the velcoity it appeared earlier to the same person running with same velocity .
The angle ( in degrees) between the initial and final velocity of rain drops with respect to ground.
View Solution
Assignement section -D (Linked Comprehension) questions and complete solutions for chapter MOTION IN A PLANE of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS MOTION IN A PLANE
- Assignement section -A Objective (one option is correct)
- Assignement section -B Objective (one option is correct)
- Assignement section -C Objective (More than one option is correct)
- Assignement section -D (Linked Comprehension)
- Assignement section -E (Assertion-Reason)
- Assignement section -F (Matrix-Match)
- Assignement section -G (Integer)
- Assignement section -H (Multiple True-False)
- Assignement section -I (Subjective )
- Assignement section -J (Aakash Challengers Questions)
- Example
- llustration 1 :
- Try yourself