Complete Solutions to ASSIGNMENT ( SECTION -B) objective type questions (one option is correct) of chapter LAWS OF MOTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | LAWS OF MOTION |
| AAKASH INSTITUTE | ASSIGNMENT ( SECTION -B) objective type questions (one option is correct) |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
A block of mass 'm' is held stationary against a rough wall by applying a force F as shown. Which one of the following statement is incorrect ?
A. Friction force = mg
B. F will not produce torque
C. Normal will not produce torque
D. Normal reaction = F
View SolutionA block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

View SolutionIn the figure shown , two blocks of masses 2 kg and 4kg are connected by a massless string which is just taut (i.e., tension is zero at this moment ). Now two forces 4 N and 15 N are applied on blocks . The tension in the string is (coefficient of static and kinetic friction are same ). [ g = `m//s^(2)`]
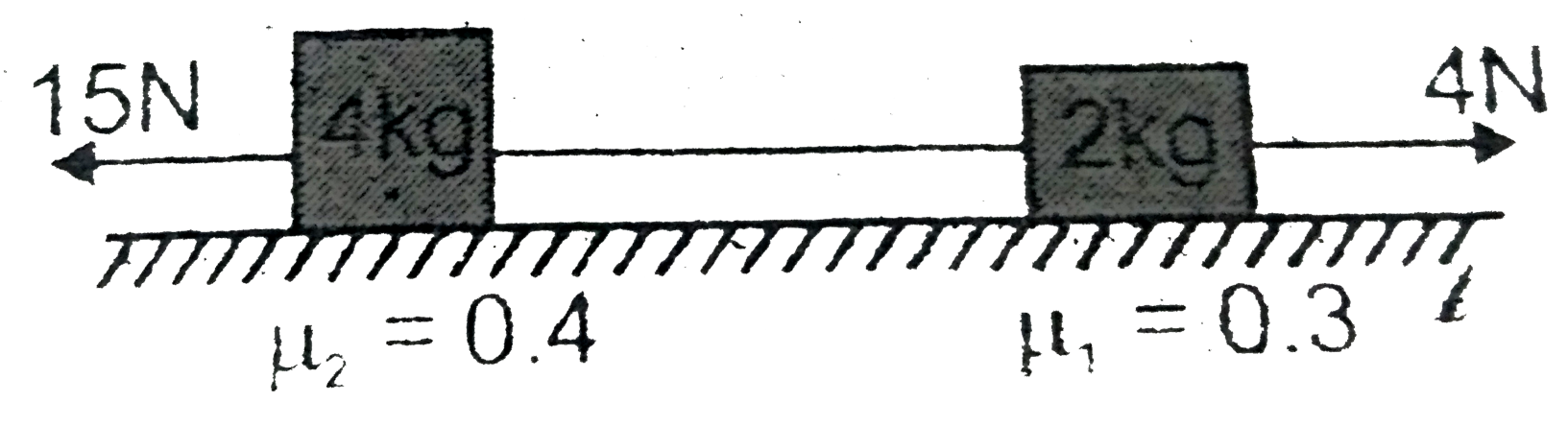
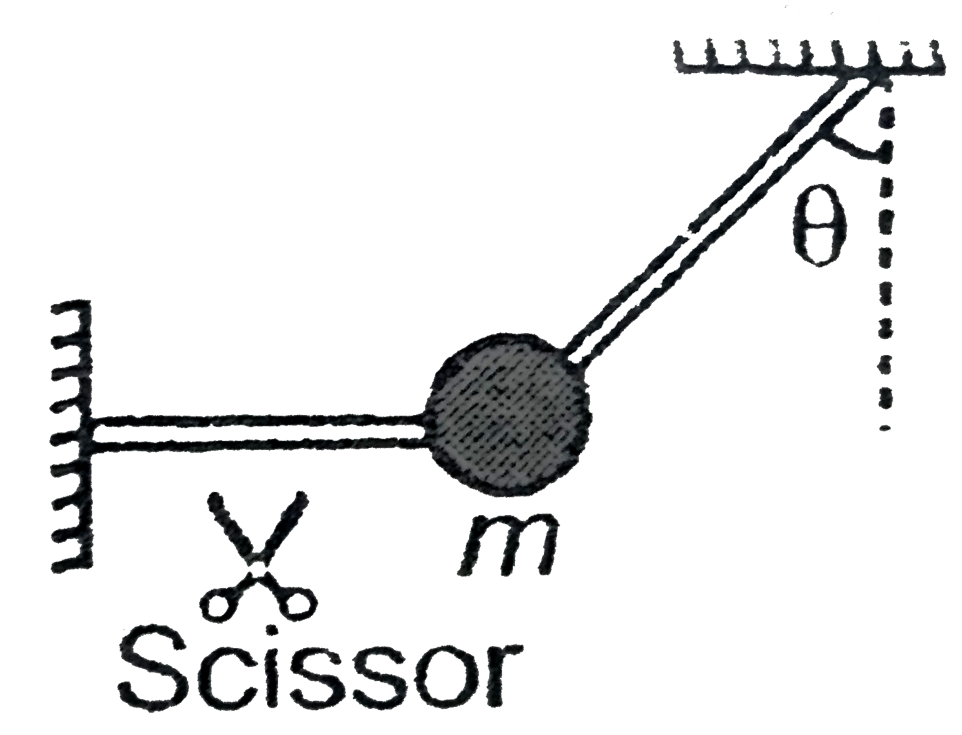
View SolutionFigure shows a small ball of mass m held at rest by means of two light and inextensible strings. The tensions in the inclined string at the instant shown and just after cutting the horizontal atring are respectively
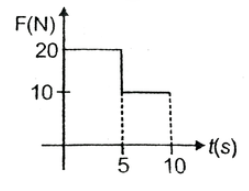
View SolutionForce is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t=10 s will be
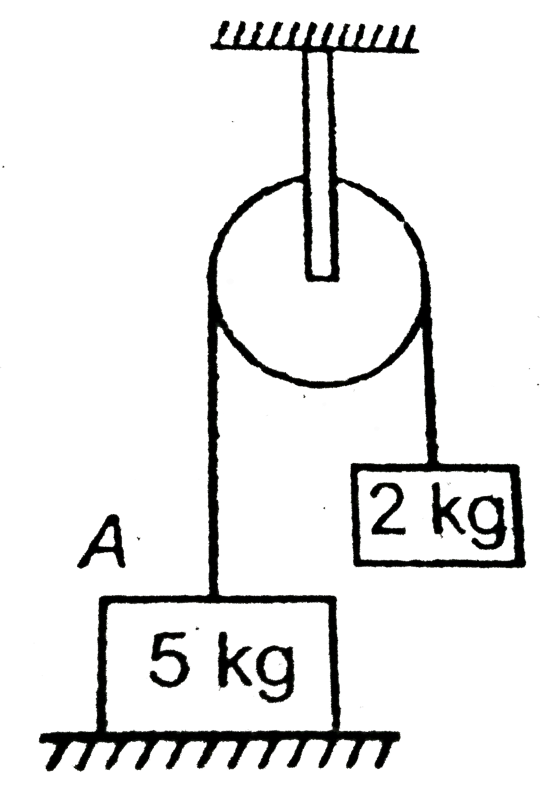
View SolutionIn the arrangement shown, what is the normal reaction the block A ( mass = 5 kg) and ground
View SolutionA block of mass 2 kg rests on the floor of an elevator , which is moving down with an acceleration 'g' , then the apparent weight of the block is [ take g = `10 m//s^(2)` ]
View SolutionA disc of radius 4 m is rotating about its fixed center with a constant angular velocity `omega` = 2 rad /s ( in the horizontal plane.) A bloc s also rotating with disc without slippng . If co- efficient of friction between the bloc and the disc is `0*4` then the maximum distance at which the block can rotate without slipping s ( g = `10 m//s^(2))` brgt
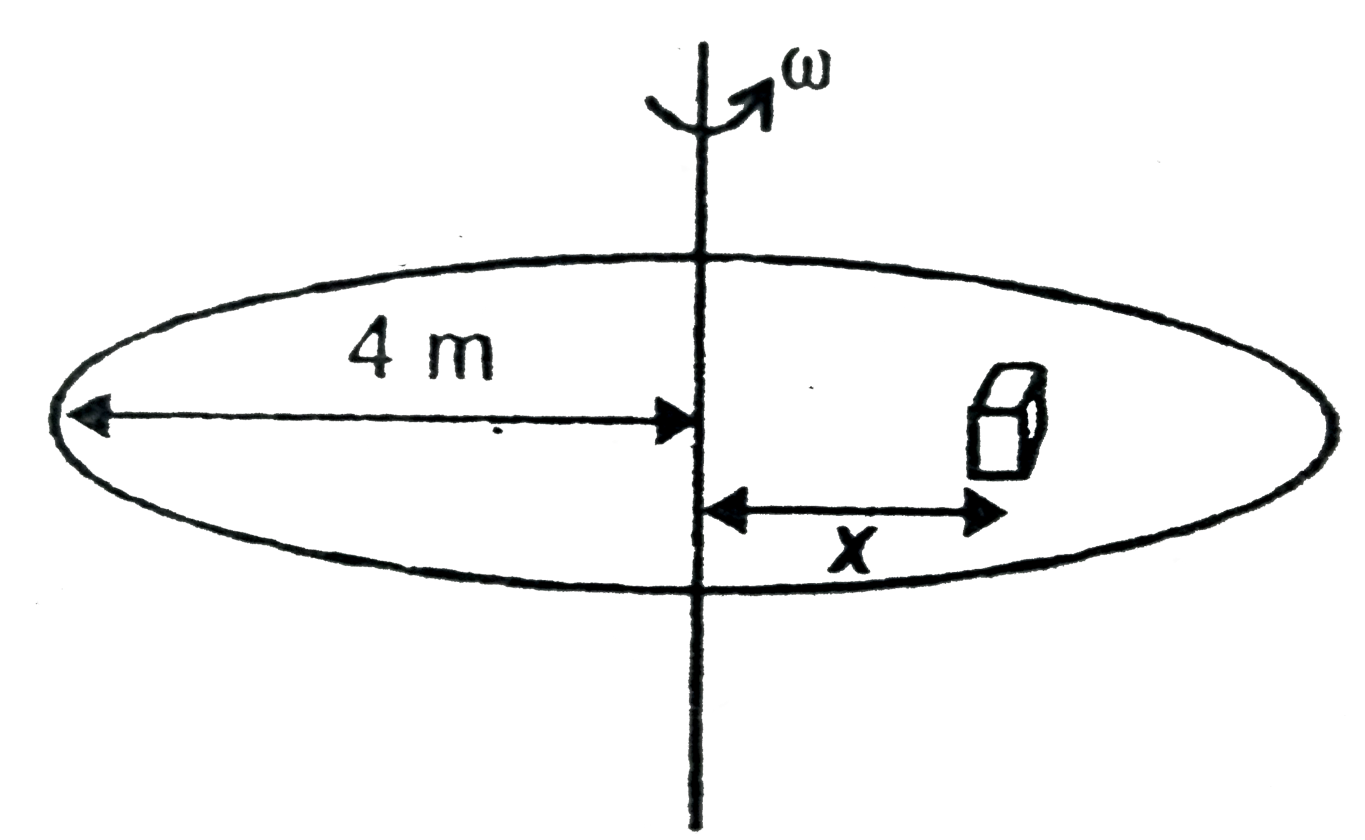
View SolutionA circular track of radius 600 m is tio be designed for cars at an average speed of 180 km/hr. What should be the angle of banking of the track?
View SolutionA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View SolutionA block of mass m is kept on a plank . The coefficient of friction between the plank and block is 1. The plank is slowly raised from one end so that it makes angle `theta` with horizontal . The forces of friction acting on the plank , when `theta = 30 ^(@) and theta 60^(@) ` are respectively,
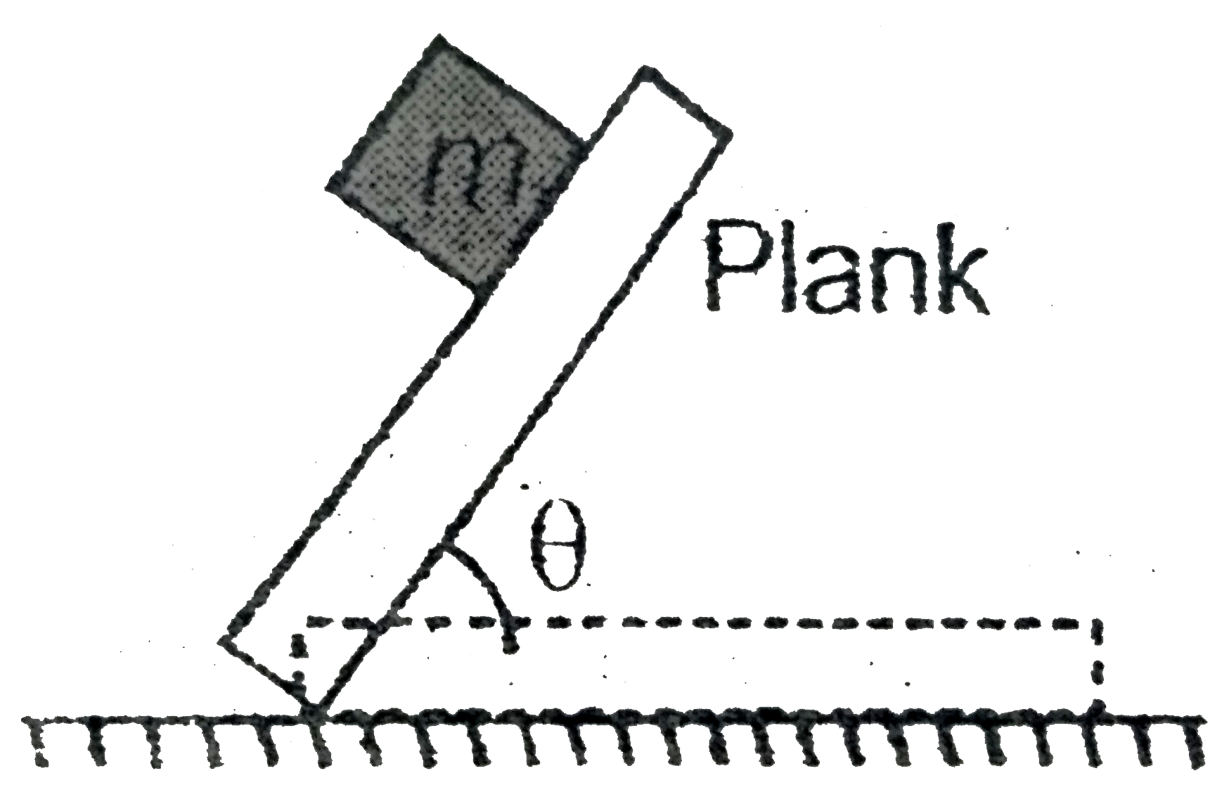
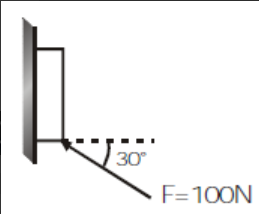
View SolutionA force of 100 N is applied on a block of mass 3 kg as shown in figure. The coefficient of friction between the surface and the block is `1/4` .Then the friction force acting on the block is
View SolutionA block of mass 5 kg is placed on a rough horizontal plane . The coefficients of stastic and kinetic friction between the block and surface are `0*5 and 0*3` respectively. A force of 100 N is applied at an angle `30^(@)` with the horizontal as shown in the figure . The acceleration of the block will be [ g = `10 m//s^(2)`]
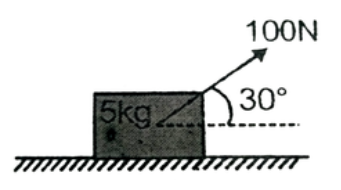
View SolutionIn the figure shown coefficient of friction between 8 kg block and surface is zero and coefficient of friction ( both static and kinetic ) between the blocks is 0.4. A force of 20 N is applied on 8 kg block as shown . The acceleration of 4 kg mass is [ g = `10 m//s^(2)`]
A. ` 4 m//s^(2)`
B. `0.5 m//s^(2)`
C. `5/3 m//s^(2)`
D. `3/5 m//s^(2)`
View SolutionIn the arrangement shown in figure coefficient of friction between 5kg block and incline plane is mu=0.5. Friction force acting on the 5kg block is

A. 20N
B. 10N
C. 15N
D. 5N
View SolutionAt a certain moment of time, acceleration of the block A is 2 `m//s^(2)` . Upward and acceleration of block B is 3 `m//s^(2)` upward. The acceleration of block C is ( masses of pulleys and string are negligible )
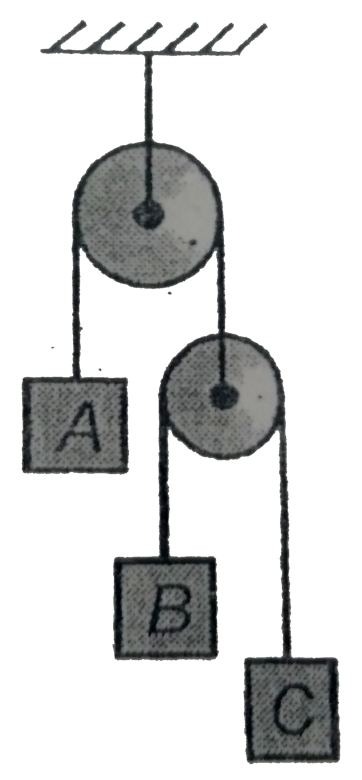
View SolutionA train is moving forward with a horizontal acceleration a. A man sitting in the train drops a coin on the floor of the train . The acceleration of the coin w.r.t man is
View SolutionIf pulley and all strings as shown are massless, then tension `T_(2) = 100 N` . Calculate weight of the block ( g = `10 m//s^(2))`
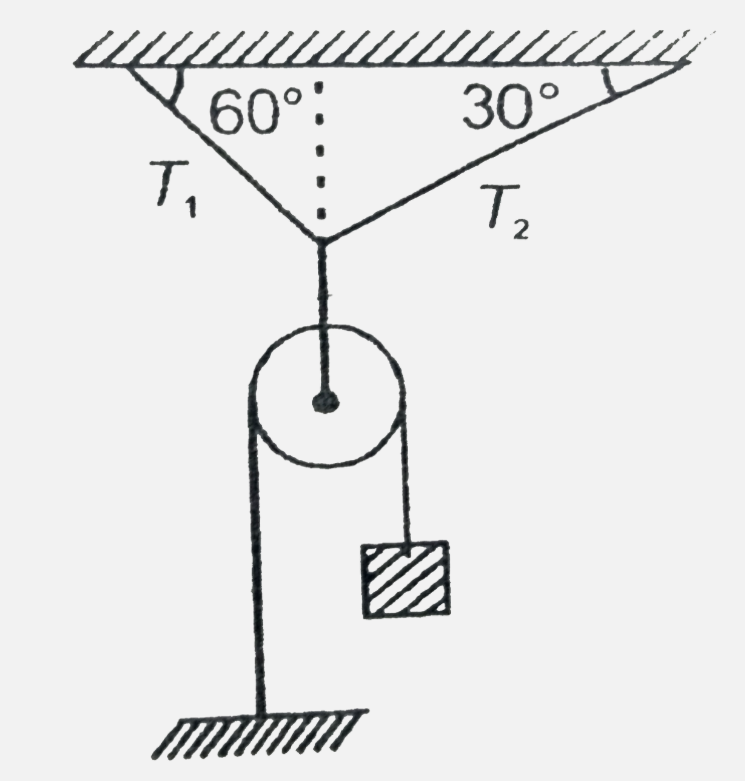
View SolutionA block of mass 2 kg rests on an inclined plane of inclination angle `37^(@)` , then calculate the force of friction acting on the block [ take g = `10 m//s^(2))`
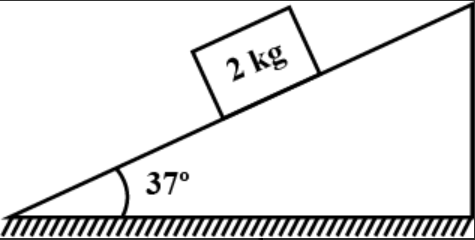
View SolutionAll surfaces shown in the figure are frictionless. A block of mass 2 kg is kept on a wedge of mass 10 kg. If the mass m remains stationary w.r.t wedge , the magnitude of force P is ( g = `10 m//s^(2))`
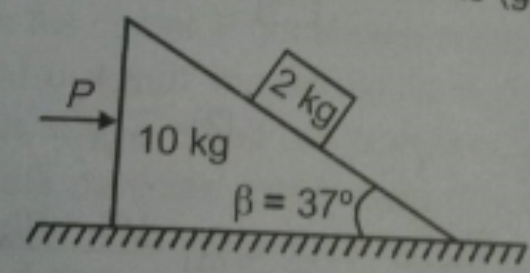
View SolutionIn the given figure the co- efficient of friction between the block and the incline plane is '1'. The acceleration with which the system should be accelerated so that the friction between the block and the wedge becomes zero ( g = ` 10 m//s^(2)`) is
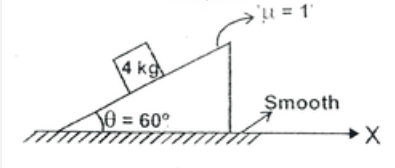
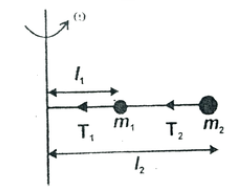
View SolutionThe whole set up shown in the figure is rotating with constant angular velocity `omega` on a horizontal frictionless table. The ratio of tensions `(T_(1))/(T_(2))` is
`("Given" (l_(2))/(l_(2)) = 2/1 )`
View SolutionA block of mass 10 kg is placed on rough inclined plane of inclination angle `37^(@)` .Coefficient of friction between block & plane is `0*8`, find minimum magnitude of F so that block remains at rest .

View SolutionA body of mass 'm' is moving with constant speed V on a track shown in figure . At point A & point B radius of curvature is R. `N_(A) , N_(B), & N_(C)` represents normal reactions at A,B,& C. Which of the gollowing option is correct ?

View SolutionThe magnitudes of accelerations of blocks of mass 2 kg and 4 kg are respectively . ( Pulleys and threads are massless) ( g = 10 `m//s^(2`)
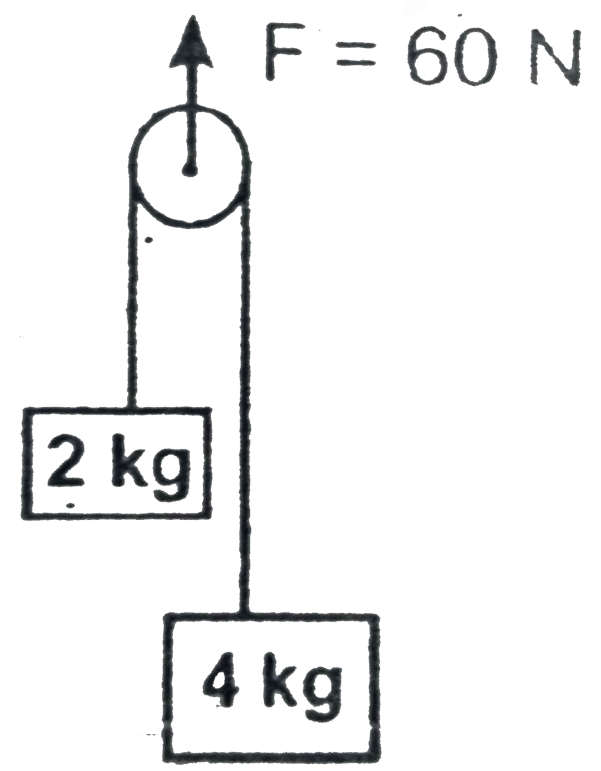
View SolutionSwimming is possible by
View SolutionWhen we jump out of a boat standing in water it moves
View SolutionA force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
View SolutionAnswer the question briefly and the point:
What is the angle of friction between two surfaces in contact having coefficient of friction `(1)/(sqrt3)`?
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is `mu` = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of `(L)/(x)`?
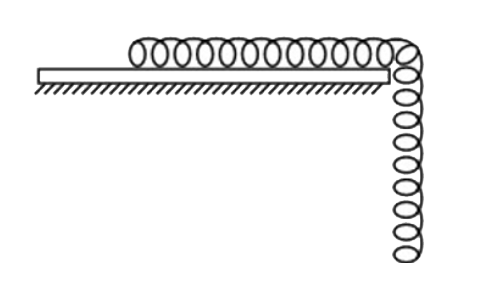
View SolutionA road is 8 m wide. Its radius of curvature is 40 m. The outer edge is above the lower edge by a distance of 1.2 m. This road is most suited for a velocity of
View SolutionFind the ratio of the extension in upper spring to lower spring
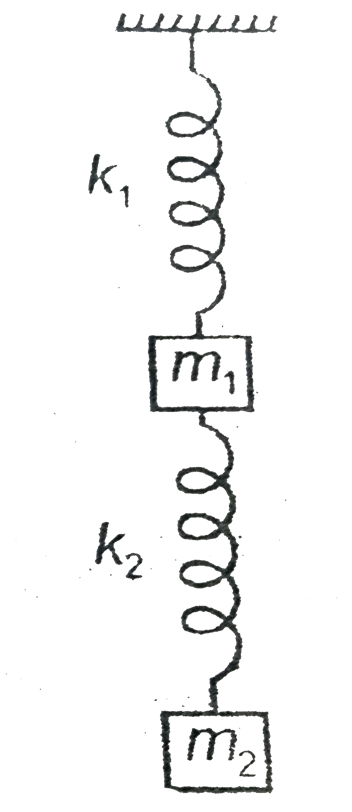
View SolutionFor the system shown in figure , to be in equilibrium , determine mass m .

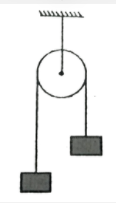
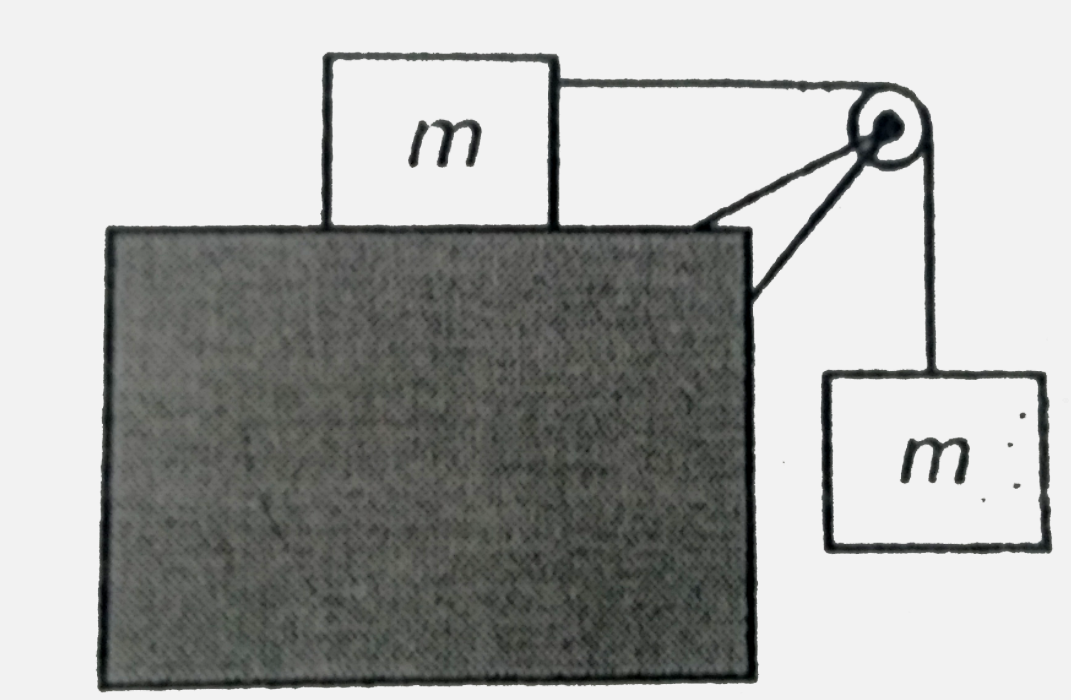
View SolutionIf two identical masses, attached by a light string passing over a light , frictionless pulley ( fixed ) of an Atwood's machine ( at different heights ) , are released from rest .
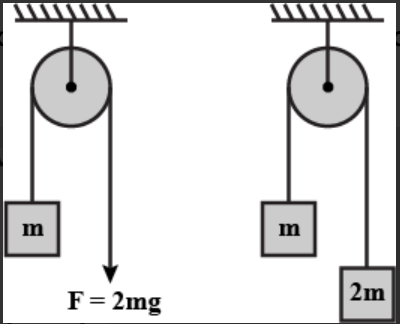
View SolutionThe magnitud of difference in accelerations of blocks of mass m in . Both the cases shown below is
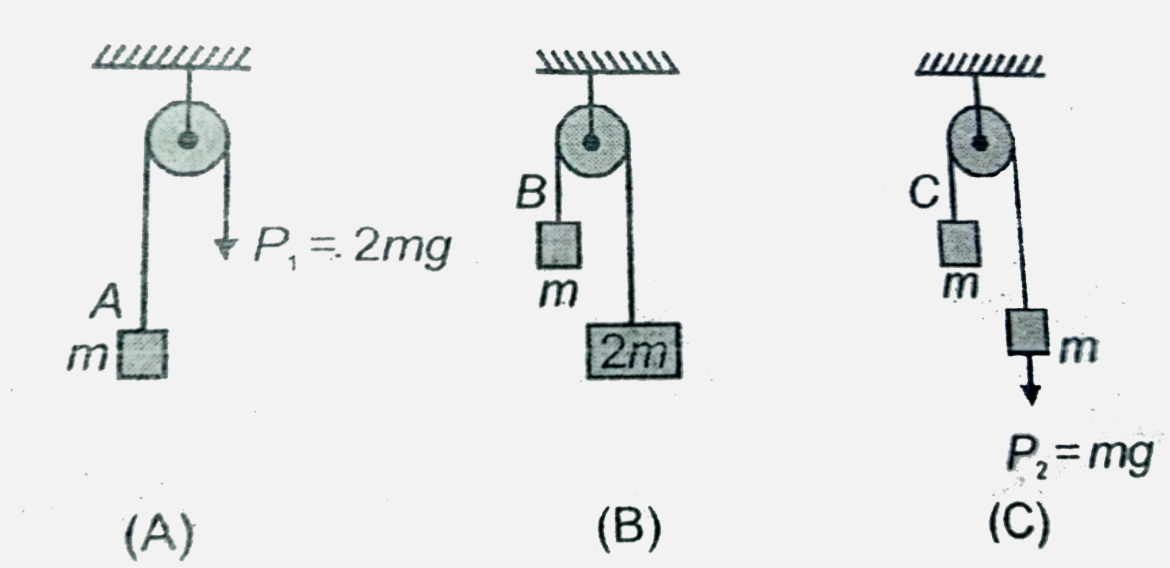
View SolutionIn the figure the blocks A, B and C of mass m each , having accelerations `a_(1) , a_(2) and a_(3)` respectively . `P_(1) and P_(2)` are external forces of magnitude 2 mg and mg respecttively .
View SolutionFigure shows a block of mass 2m sliding on a block of mass m. Find the acceleration of each block . ( All surface are smoth )
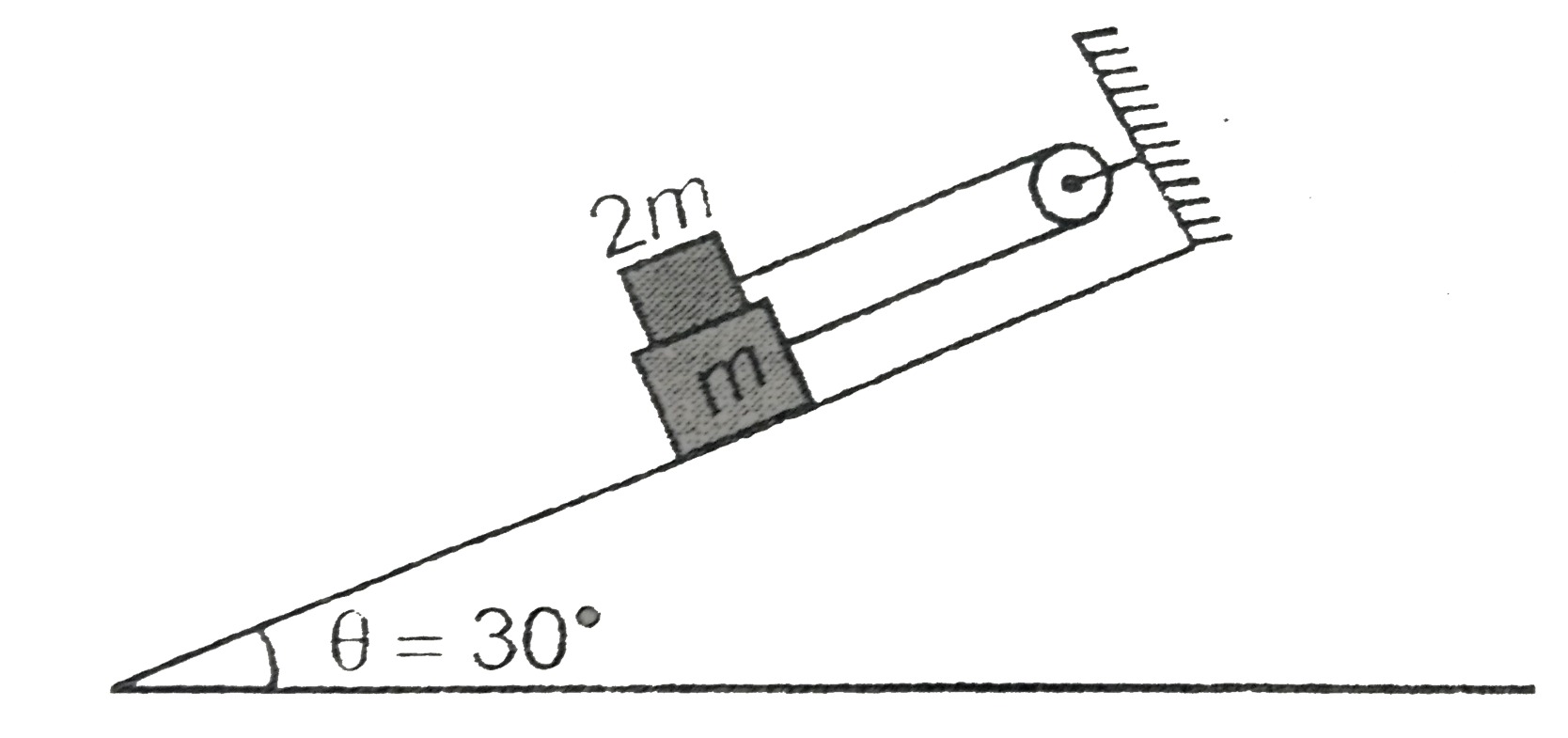
View SolutionTwo identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
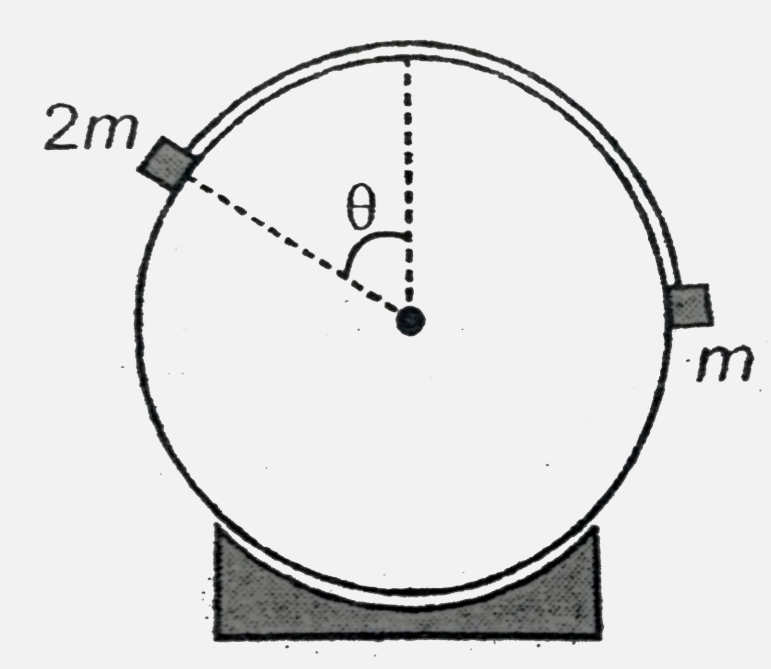
View SolutionA mass 2m lies on a fixed , smooth cylinder . An ideal string attached to 2m passes over the cylinder to mass m . Then the value of angle `theta` for which system is in equilibrium
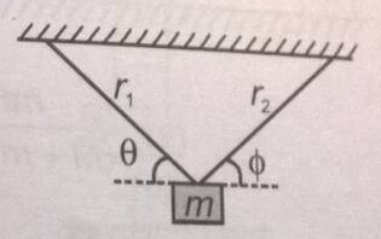
View SolutionA block is suspended by two light ropes ` r_(1) and r_(2)` as shown in figure . Then what is the tension the rope `r_(2)`
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionA block of mass 10 kg is suspended through two light spring balances as shown in figure

View SolutionTwo blocks of masses M and 2M are connected to each other through a light spring as shown in figure . If we push the mass M with a force F which cause acceleration a in mass M. what will the acceleration in 2M?
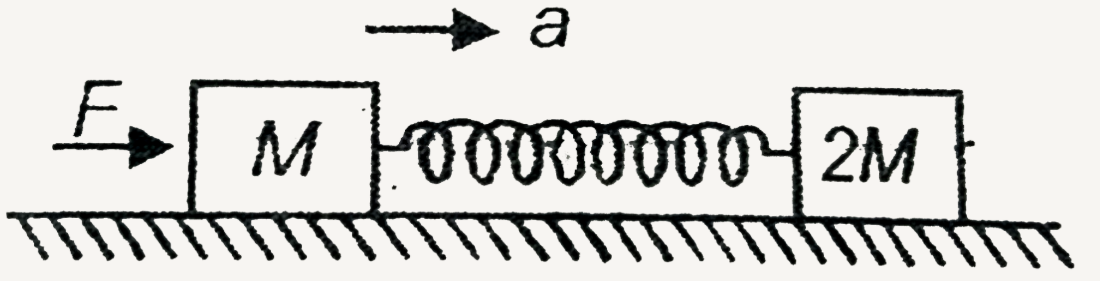
View SolutionThree masses `m_(1) ,m_(2) and m_(3)` are attached to a string -pulley system as shown . All the three masses are held at rest and then released If `m_(3) ` remains at rest , then

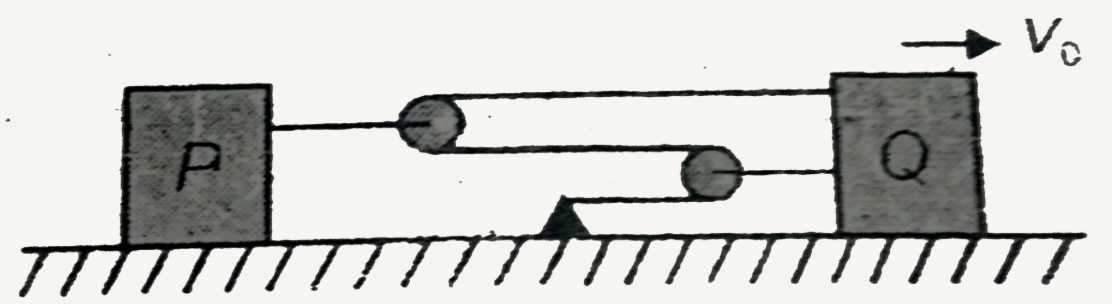
View SolutionThe block Q moves to the right with a constant velocity `v_(0)` as shown in figure. The relatives velocity of body P with respect to Q is ( assume all pulleys and strings are ideal)
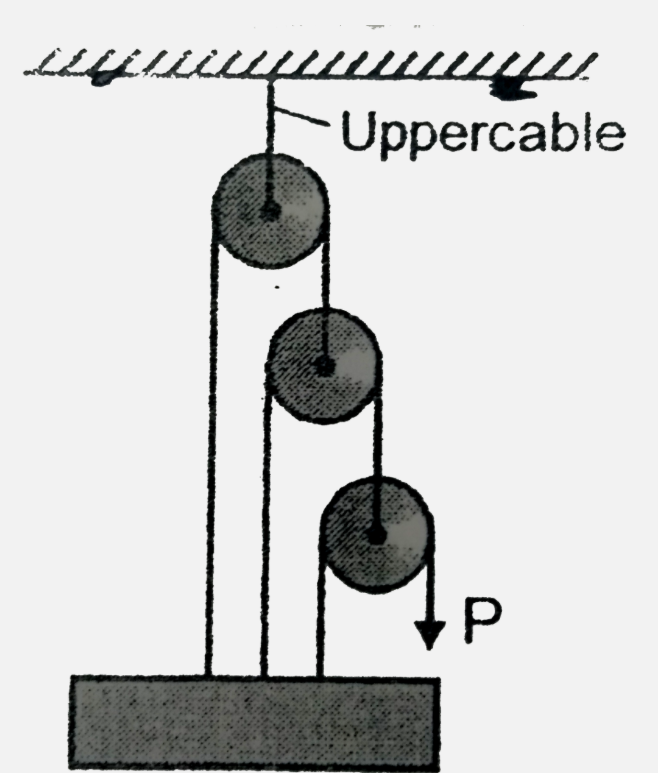
View SolutionThe pull P is just sufficient to keep the 14 N block in equilibrium as shown . Pulleys are ideal . Find the tension ( in N) in the upper cable connected with celling
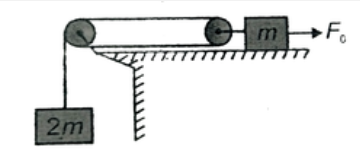
View SolutionA block of mass m on a smooth horizontal surface is. Connected to a second mass 2m by a light cord over a light frictionless pulley as shown. ( Neglect the mass of the cord and of the pulley). A force of magnitude `F_(0)` is applied to mass m as shown. Neglect any fiction . Find the value of force `F_(0)` for which the system will be in equilibrium
View SolutionWith what force must a man pull on the rope to hold the plank in position it the man weights 60 kg? Neglect the weight of the plank, rope and pulley ( Take g= `10m//s^(2))`

View SolutionBlocks P and R starts from rest and moves to the right with acceleration `a_(p) = 12t m//s^(2) and a_(R) = 3 m//s^(2)`. Here t is in seconds . The time when block Q again comes to rest is
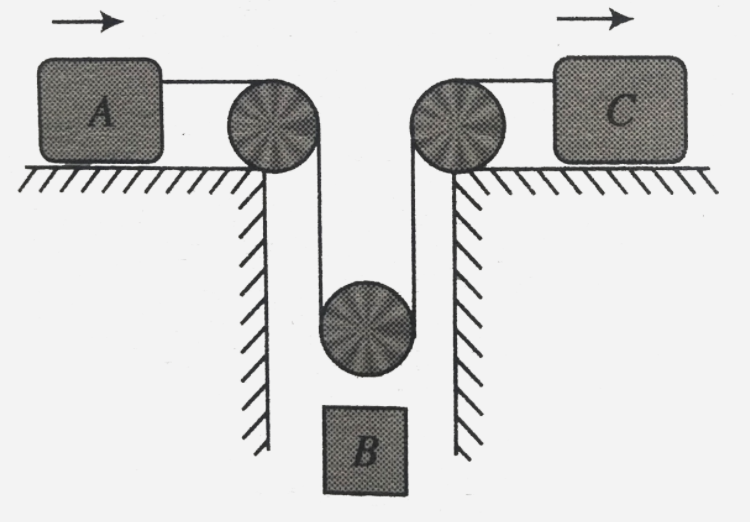
View SolutionIn the arrangement , shown below pulleys are massless and frictionless and threads are inextensible , block of mass `m_(1)` will remain at rest if
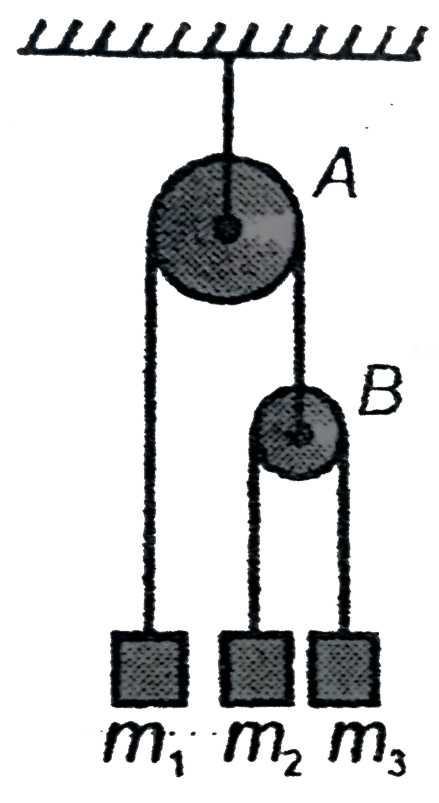
View SolutionIn the arrangement shown in fig. `m_(1)=1kg, m_(2)=2 kg`. Pulleys are massless and strings are light. For what value of M, the mass `m_(1)` moves with constant velocity.

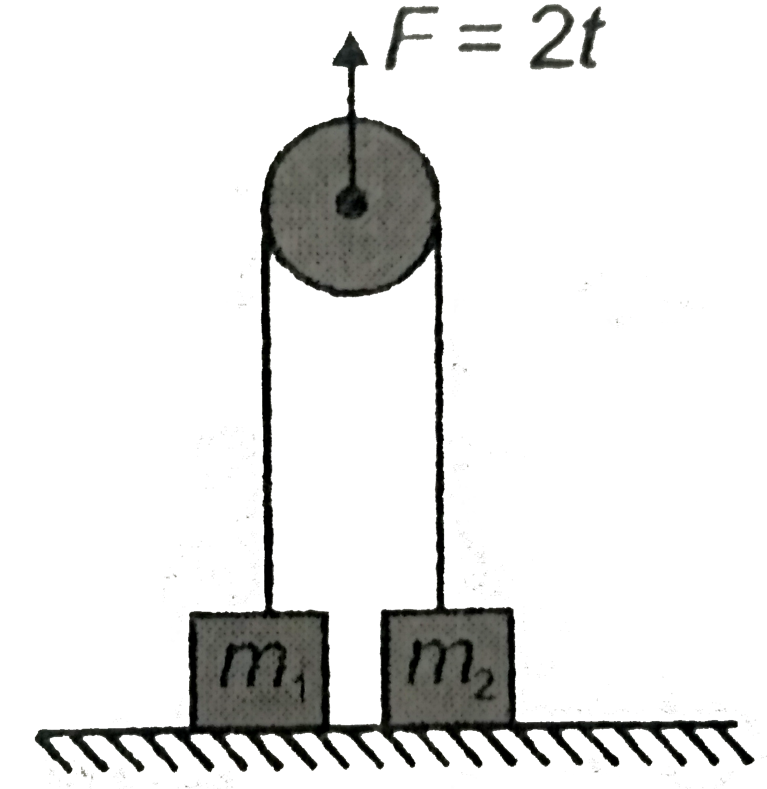
View SolutionIn the figure shown `m_(1) = 1 kg , m_(2) = 2 kg `, pulley is ideal . At t = 0 , both msses touches the ground and string is tout . A force F = 2t is applied to pulley ( t is in second ) then `m_(1)` is lifted off the ground at time ( g = 10 `m//s^(2))`
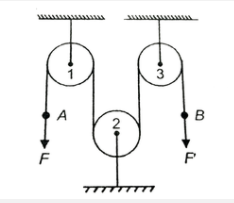
View SolutionThe tension at any point of the string AB will be same if
View SolutionIn the following diagram a massless pulley is pulled by a constant force of magnitude P. There is no friction between the block and the floor. The acceleration produced in the block of mass m is
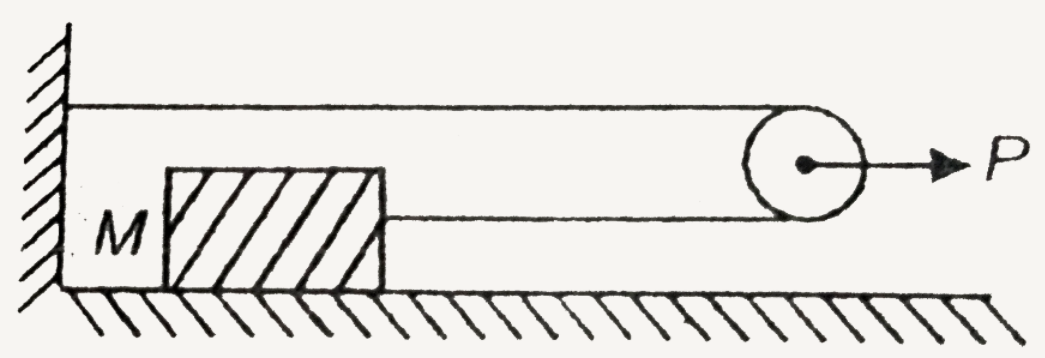
View SolutionA price of length 1 m and mass 1 kg is suspended vertically from one end of a massless string passing on asmooth , fixed pulley . A ball of mass 2 kg is attached to the other end from the position shown . Time taken by the ball to cross the pipe is shown. Time taken by the ball to cross the pipe is
View SolutionA particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals `omega`, then
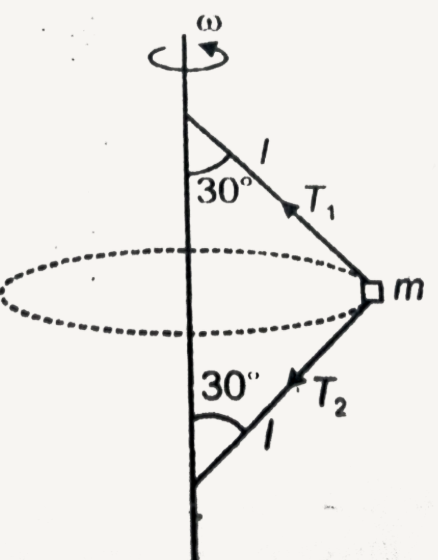
View SolutionA particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals `omega`, then
`T_(1)` equals
View SolutionA car is taking a turn of radius 400 m on a horizontal circle . Coefficient of friction between the ground and tyres of car is 0.2 . Find the maximum speed with a safe turn can be taken
View SolutionA ball of mass 'm' is rotating in a circle of radius 'r' with speed v inside a smooth cone as shown in figure. Let N be the normal reaction on the ball by the cone .then choose the wrong option.

View Solution
ASSIGNMENT ( SECTION -B) objective type questions (one option is correct) questions and complete solutions for chapter LAWS OF MOTION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS LAWS OF MOTION
- ASSIGNMENT ( SECTION -A)
- ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
- ASSIGNMENT ( SECTION -C) objective type questions (More than one options are correct)
- ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question
- ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question (Comprehension -I)
- ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question (Comprehension -II) (Choose the correct answer :)
- ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question (Comprehension -III) (Choose the correct answer :)
- ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question (Comprehension -IV) (Choose the correct answer :)
- ASSIGNMENT ( SECTION -E) Assertion - Reason Type Questions
- ASSIGNMENT ( SECTION -F ) Matrix - Match Type Questions
- ASSIGNMENT ( SECTION -G ) Integer Answer Type Questions
- ASSIGNMENT ( SECTION -H ) Multiple True - False Type Questions (Identify the correct combination of true (T) and false (F) of the given three statements.)
- ASSIGNMENT ( SECTION -I ) Subjective Type Questions
- ASSIGNMENT ( SECTION -J ) Aakash Challengers Questions
- Assignment (SECTION-A)
- Assignment (SECTION-B)
- Assignment (SECTION-C)
- Assignment (SECTION-D) (Assertion-Reason Type Questions)
- Example
- EXAMPLES
- EXERCISE
- Illustration
- TRY YOURSELF