Complete Solutions to Example of chapter MOVING CHARGES AND MAGNETISM of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOVING CHARGES AND MAGNETISM |
| AAKASH INSTITUTE | Example |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
A chagre particle having charge 2 C is thrown with velocity `2hati+3hatj` inside a region `E=2hatj` and magnetic field `5hatk` Find the initial Lorentz force action on the particle
View SolutionA charged particle of charge 1 mC and mass 2g is moving with a speed of 5m/s in a uniform magnetic field of 0.5 tesla. Find the maximum acceleration of the charged particle
View SolutionA charged particle of specific charge (i.e charge per unit mass) 0.2 C/kg has velocity `2 hat(i) - 3 hat(j)` (m/s) at some instant in a uniform magnetic field `5 hat(i) + 2 hat(j)` (tesla). Find the acceleration of the particle at this instant
View SolutionA charged particle moving in a magnetic field `vecB=hati-hatj` tesla, has an acceleration of `2hati+alpha hatj(m//s^(2))` at some instant. Find the value of `alpha`
View SolutionFind the instantaneous direction of force in following case (magnetic field and velocity are indicated)
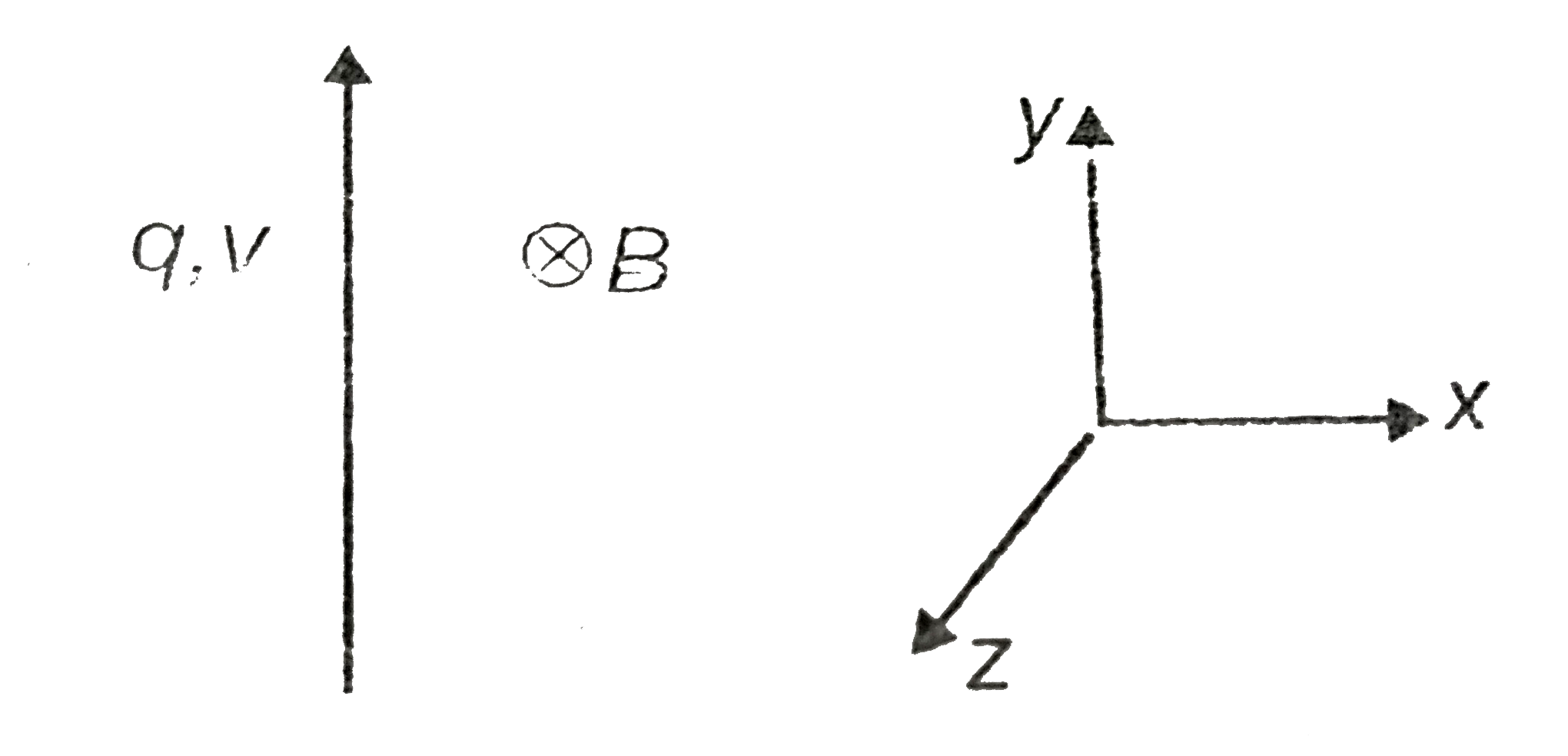
View SolutionThe horizontal component of earth's magnetic field at a certain place is ` 3xx 10^(-5) T` and the direction of the field is from the geographic south to the geographic north. A very long straight conductor is carrying a steady current of 1 A. What is the force per unit length on it when it is placed on a horizontal table and the direction of current is from east to west ?
View SolutionA straight wire of mass 400 g and length 2m carries a current of 2A. It is suspended in mid air by a uniform horizontal field B. What is the magnitude of the magnetic field ?
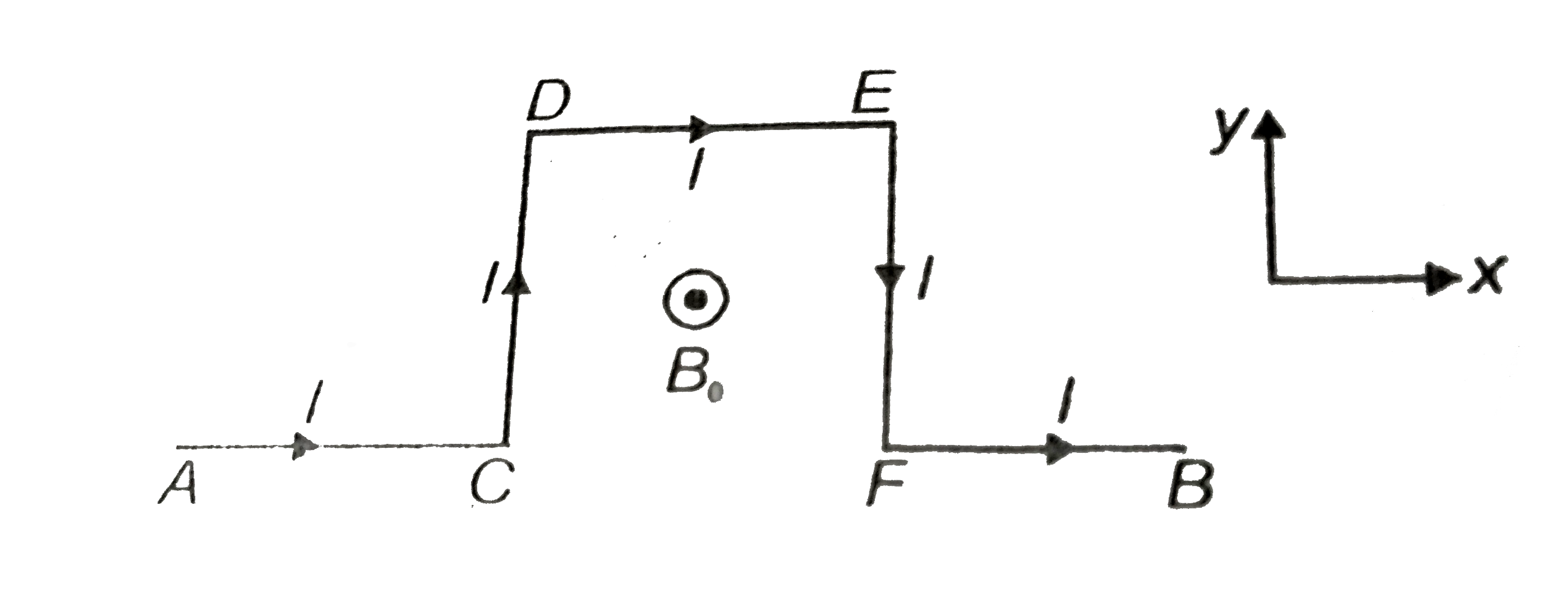
View SolutionA uniform magnetic field `vec(B) = B_(0) hat(k)` exists in a region. A current carrying wire is placed in x-y plane as show. Find the force acting on the wire AB, if each section of the wire is of length 'a'.
View SolutionA proton and an `alpha`-particle, accelerated through same potential difference, enter a region of uniform magnetic field with their velocities perpendicular to the field. Compare the radii of circular paths followed by them.
View SolutionIf a charged particle is thrown with double the speed in a region of transverse magnetic field, how do its radius and time period of revolution change?
View SolutionFour particles enter a region of uniform magnetic field. Their trajectories are shown in figure. What are the signs of the charge of all four particles ?
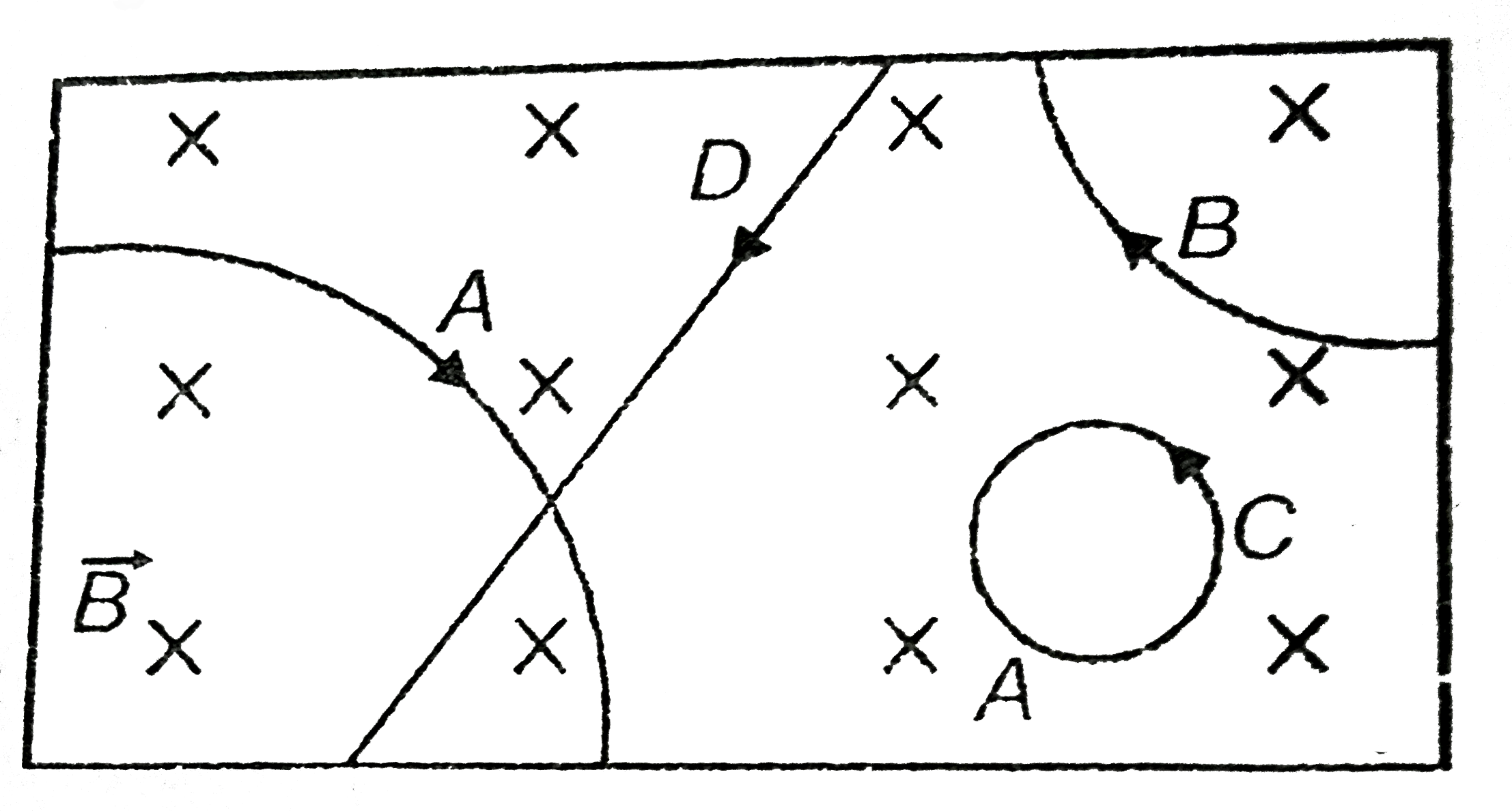
View SolutionTwo protons are projected with different velocities in a region having uniform magnetic field that is perpendicular to their velocities. The region is large enough that the protons can execute complete circular trajectories. How do the radii of their circular paths compare? Which particles takes longer to complete one revolution?
View SolutionA beam of proton with a velocity of `4xx10^(5)ms^(-1)` enters a uniform magnetic field of 0.3 T at an angle of `60^(@)` to the magnetic field/The radius of helical path taken by proton beam is
View SolutionA proton, an electron, a neutron, an `alpha`-particle and an unknown particle enter a region of magnetic field with equal momental. Figure shows paths (market 1 to 5) followed by these particles. Identify which path corresponds to which particle
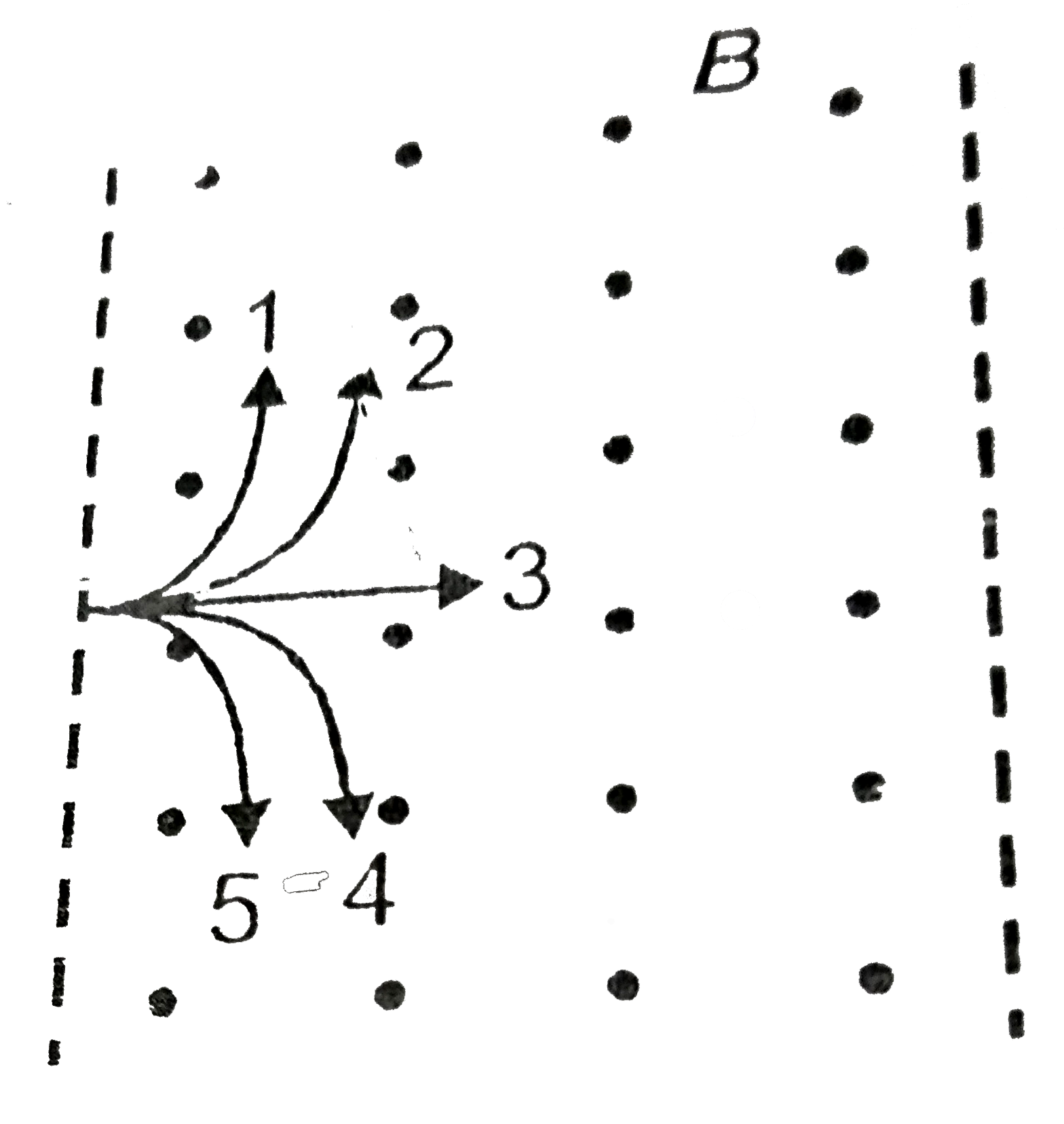
View SolutionThe magnetic field applied in a cyclotron is 3.5 T. What will be the frequency of electric field that must be applied between the does in order to accelerate protons ?
View SolutionMagnetic field applied on a cyclotron is `0*7T` and radius of its dees is `1*8m`. What will be the energy of the emergent protons in `MeV`? Mass of proton`=1*67xx10^-27kg`.
View SolutionA current carrying conductor of length `l` is bent into two loops one by one. First loop has one turn of wire and the second loop has two turns of wire. Compare the magnetic fields at the centre of the loops
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
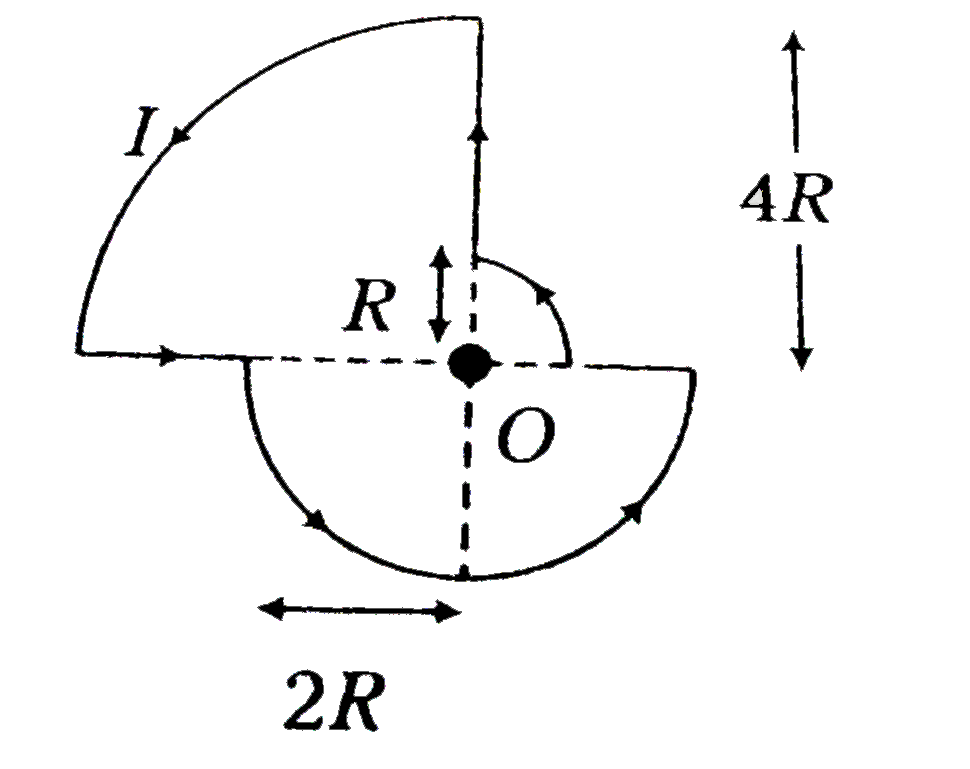
View SolutionWrite equation for Ampere's circuital law for the Amperian loop shown (traversed in the direction shown by arrow marks put on it)
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

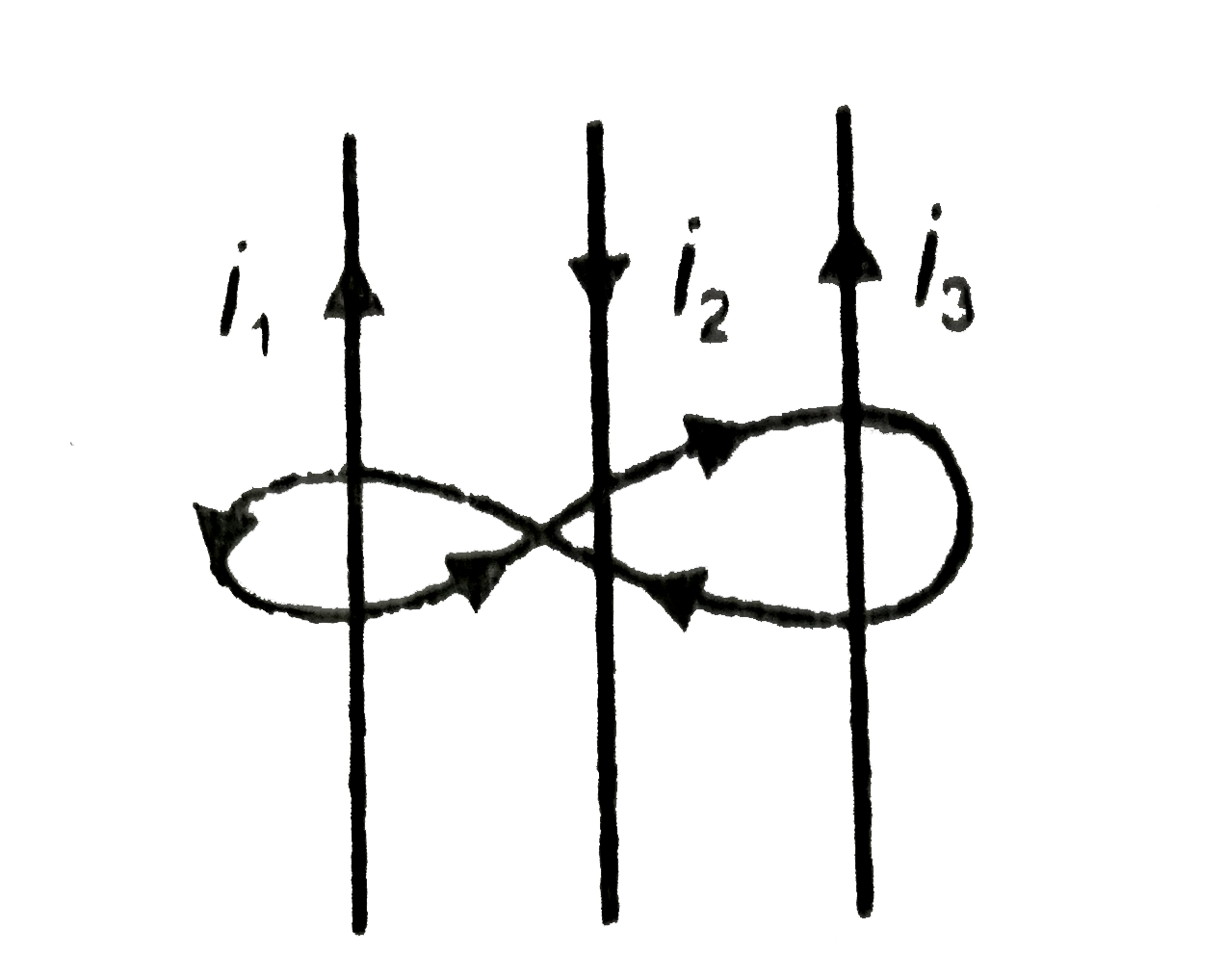
View SolutionWhat is the net magnetic field at point O for the current distribution shown here?
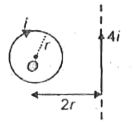
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region `r lt a and r gt a`

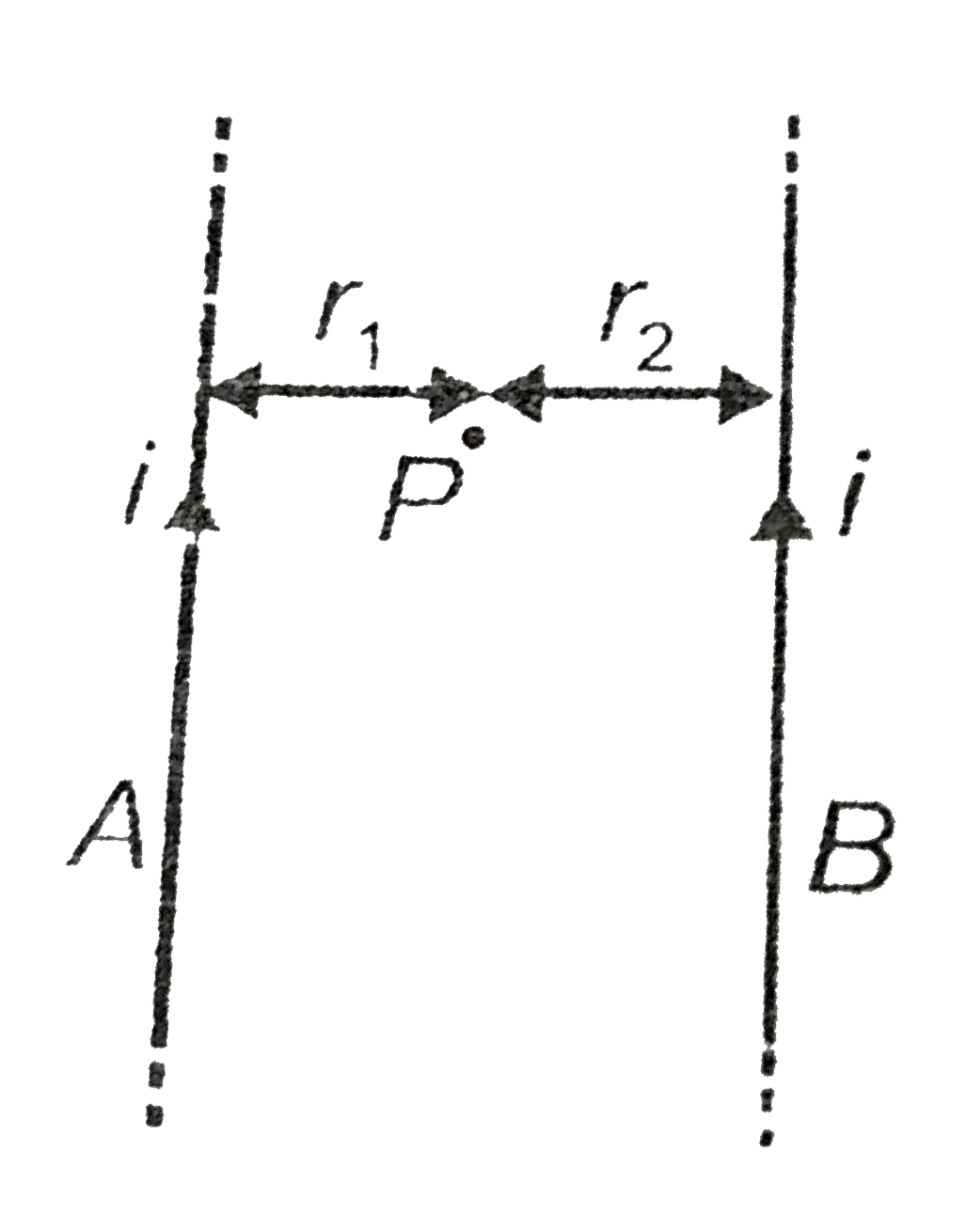
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given `r_(1) gt r_(2)`
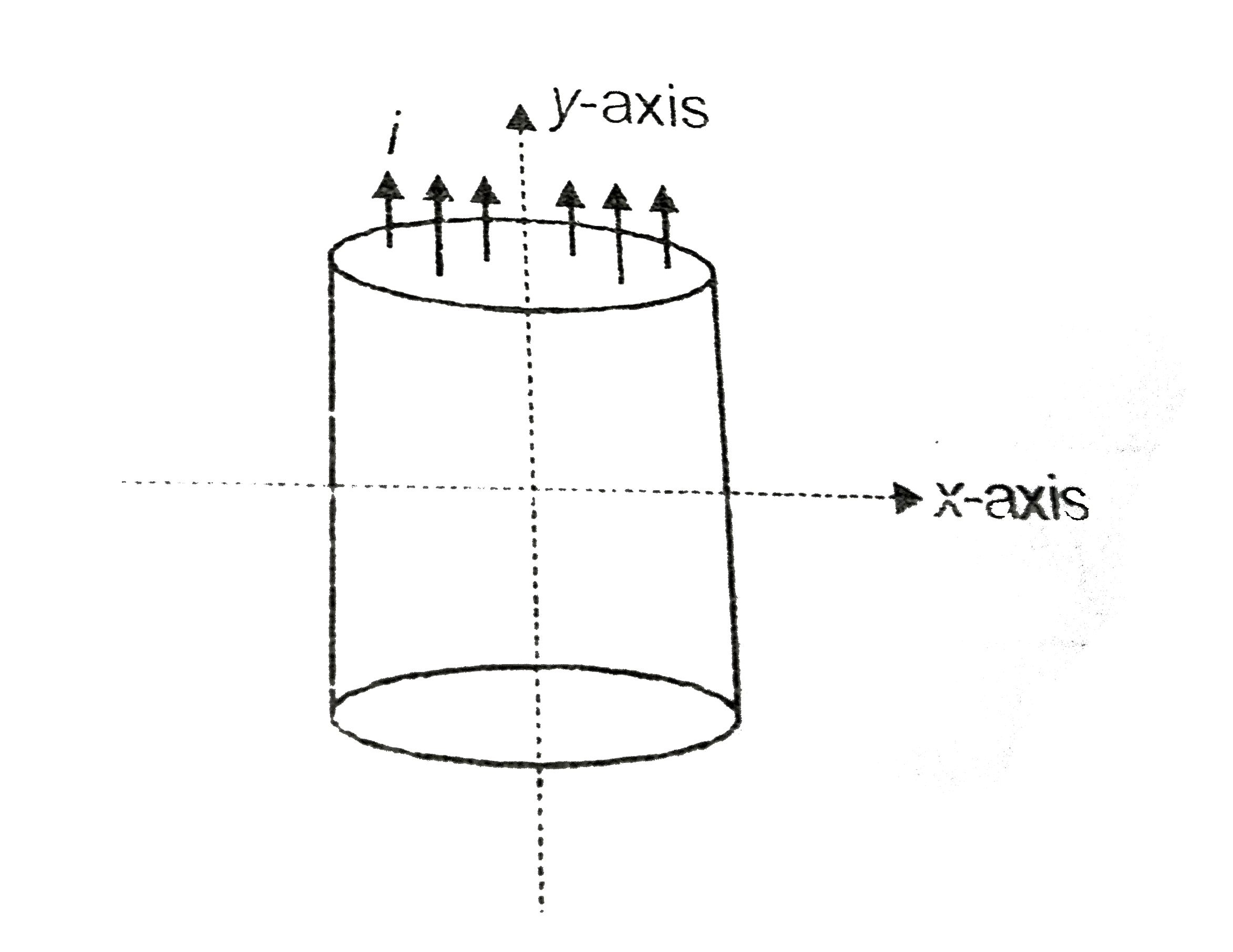
View SolutionA solenoid 50 cm long has 4 layers of windings of 350 turns each. If the current carried is 6A, find the magnetic field at the centre of the solenoid.
View SolutionA square loop OABCO of side I carries a current i. It is placed as shown figure.Find the magnetic moment of the loop

View SolutionCurrent is flowing in a wire frame kept as shown in the figure where EDCF is in y-z plane and AFCB is in x-z plane. Current in the wire frame is i and length of each side is a. Find the magnetic moment

View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field `B_(0)` Tesla in x-y plane as shown in figure. The loop carries a current `i = 1A` in the direction shown. Find the torqure acting on the loop
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed `omega` about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA galvanometer has a resistance of 30 ohm and a current of 2 mA is needed to give a full scale deflection. What is the resistance needed and how is it to be connected to convert this galvanometer
(a) Into an ammeter of 0.3 A range ?
(b) Into a volmeter of 0.2 V range ?
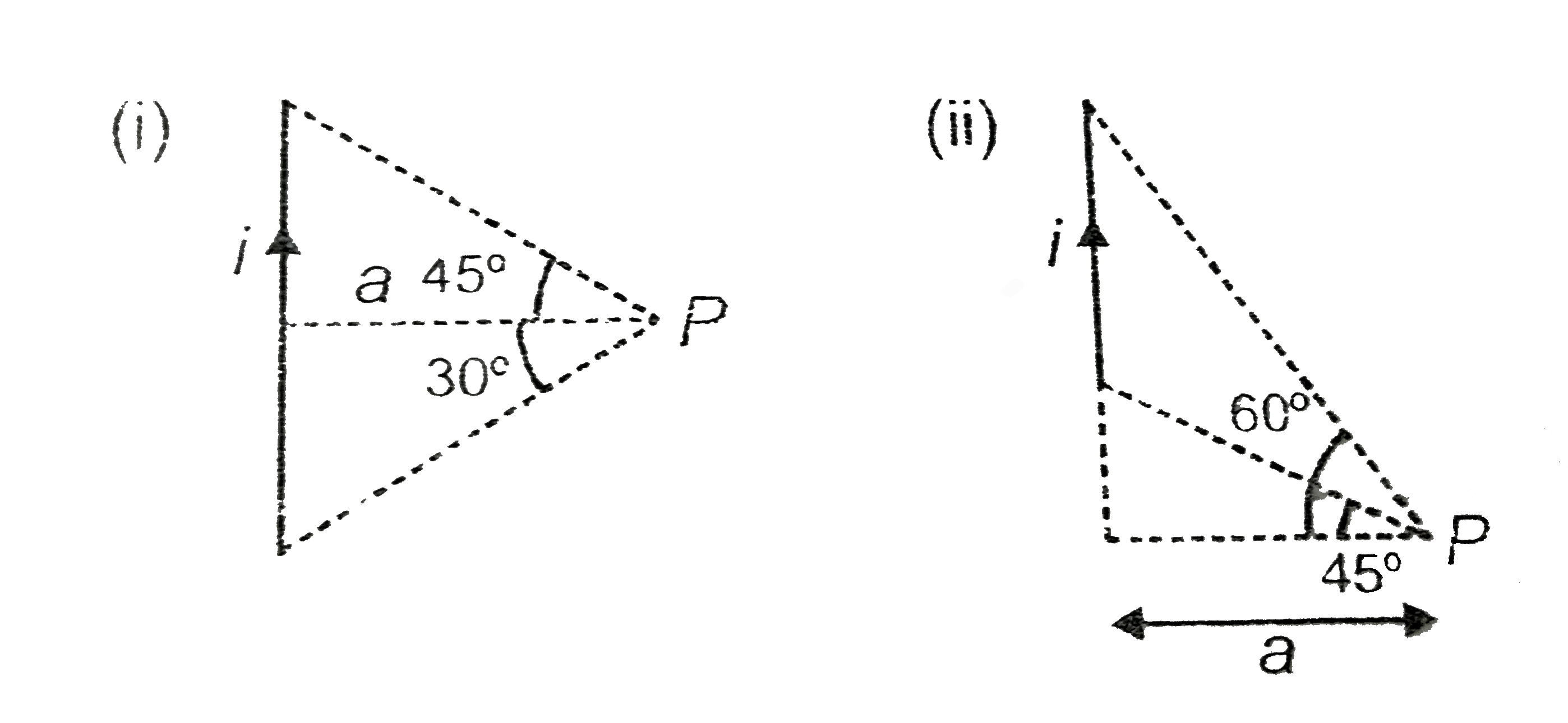
View SolutionWhat are value of `phi_(1), phi_(2)` and r to find out magnetic field at P in the following cases ?
View SolutionFigure shows a long and thin strip of width b which carries a current `I`. Find magnetic induction due to the current in strip at point P located at a distance `r` from the strip in the plane of strip as shown in figure-4.35.

View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.2m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionA current loop is bent in the form of a rectangule of sides a and b as shown. The current flowing through the loop is i and its direction is shown in the figure. Calculate the magnetic field at the centre of the rectangle
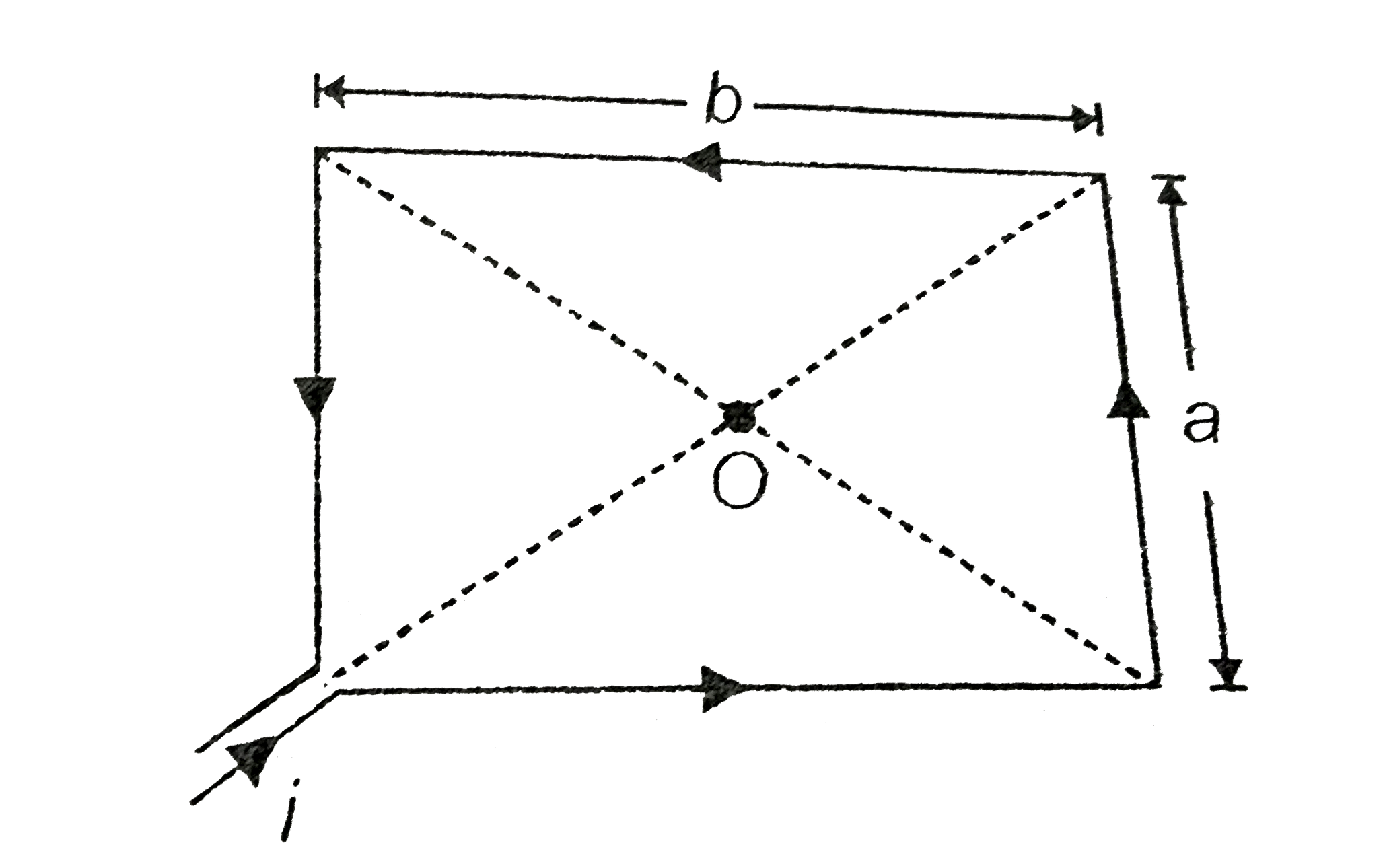
Strategy : Due to each side of the rectangle, field at O is perpendicular to the plane of paper adn outwards (you can check it using Right Hand Thumb Rule). So the fields can be added up to find net magnetic field.
View SolutionFind the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle `theta` at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element `i vec(dl)` as shown. The field due to this element at the centre can be obtained by Biot-Savart law
View SolutionA current enters a uniform conducting loop of radius r at X and leaves at Y
(i) What is magnetic field at O due to arc portions XBY and XAY of the loop ?
(ii) What is net magnetic field at O ?

View SolutionThe figure shows a long straight current carrying conductor. Can you plot the variation of magnetic field on x-axis ?
View SolutionCan you use Ampere's law of find the magnetic field at the centre of a ring of radius R and carrying current l?
View SolutionConsider a system of two long coaxial cylinders: solid (of radius a carrying i current in positive z direction) and hollow (or radius b carrying current i in negative z direction). Find the magnetic field at a point distant r from of the cylinders for
(i) `r le a`
(ii) `a lt r lt b`
(iii) `r gt b`

View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as `J = kr^(2)`, where, k is a constant. Find an expression for the magnetic field B at a distance `r (lt R)` from the axis

View SolutionA proton and an `alpha`-particle, accelerated through same potential difference, enter a region of uniform magnetic field with their velocities perpendicular to the field. Compare the radii of circular paths followed by them.
View SolutionIf a charged particle is thrown with double the speed in a region of transverse magnetic field, how do its radius and time period of revolution change?
View SolutionThere exists a uniform magnetic field `vec(B) = +B_(0) hat(k) " for " x gt 0 and vec(B) = 0` for all `x lt 0`. A charged particle placed at `(0, -a,0)` is given an initial velocity `vec(v) = v_(0) hat(i)`. What is the magnitude and nature of charge on the particle such that it crosses through the origin ?
Strategy: When the charge is projected perpendicular to a uniform magnetic field, it follows a circular path. In this case, the force acting on it will be directed either towards +y-axis. or y-axis. It is given that it crosses point O. Thus, the force at `(0, -a, 0)` must be towards y-axis
View SolutionA particle of charge q and mass m released from origin with velocity `vec(v) = v_(0) hat(i)` into a region of uniform electric and magnetic fields parallel to y-axis. i.e., `vec(E) = E_(0) hat(j) and vec(B) = B_(0) hat(j)`. Find out the position of the particle as a functions of time
Strategy : Here `vec(E) || vec(B)`
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
`a_(y) = (F_(y))/(m) = (F_(e))/(m) = (qE_(0))/(m)`
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
`vec(v) (t) = v_(x) hat(i) + v_(y) hat(j) + v_(z) hat(k)`
View SolutionA long wire is bent to form a rectangular section and is placed in a region with a uniform magnetic field, as shown in figure. The magnetic field is directed downward and has a magnitude of 2.5 T. The wire carries a 25-A current. Find the net torque on the wire about the z-axis

View SolutionThe figure shows top view of a conducting rob AB, bent to form a semicircle of radius R, carrying current I, placed on a smooth horizontal table. It is subjected to a uniform magnetic field B perpendicular to its plane as shown. The rod is held at rest in its position by two light strings attached to its ends. Calculate the magnetic force acting on the conductor AB and the tension in the strings.
Strategy: To find the force conductor, consider a small arc of length `dl = Rd theta`. This arc can be consider as a straight conductor of length dl.
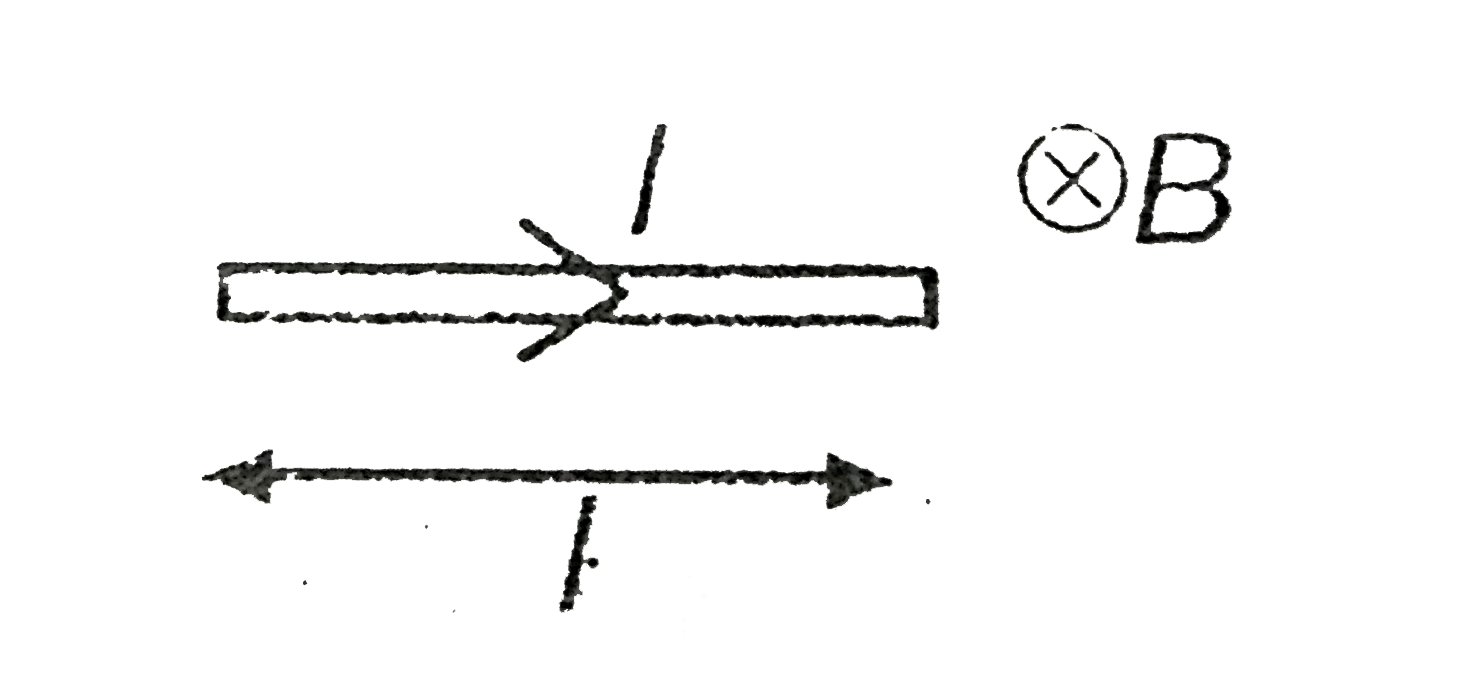
View SolutionWhat is the magnetic force acting on the finite wire due to the fixed infinite wire shown here?
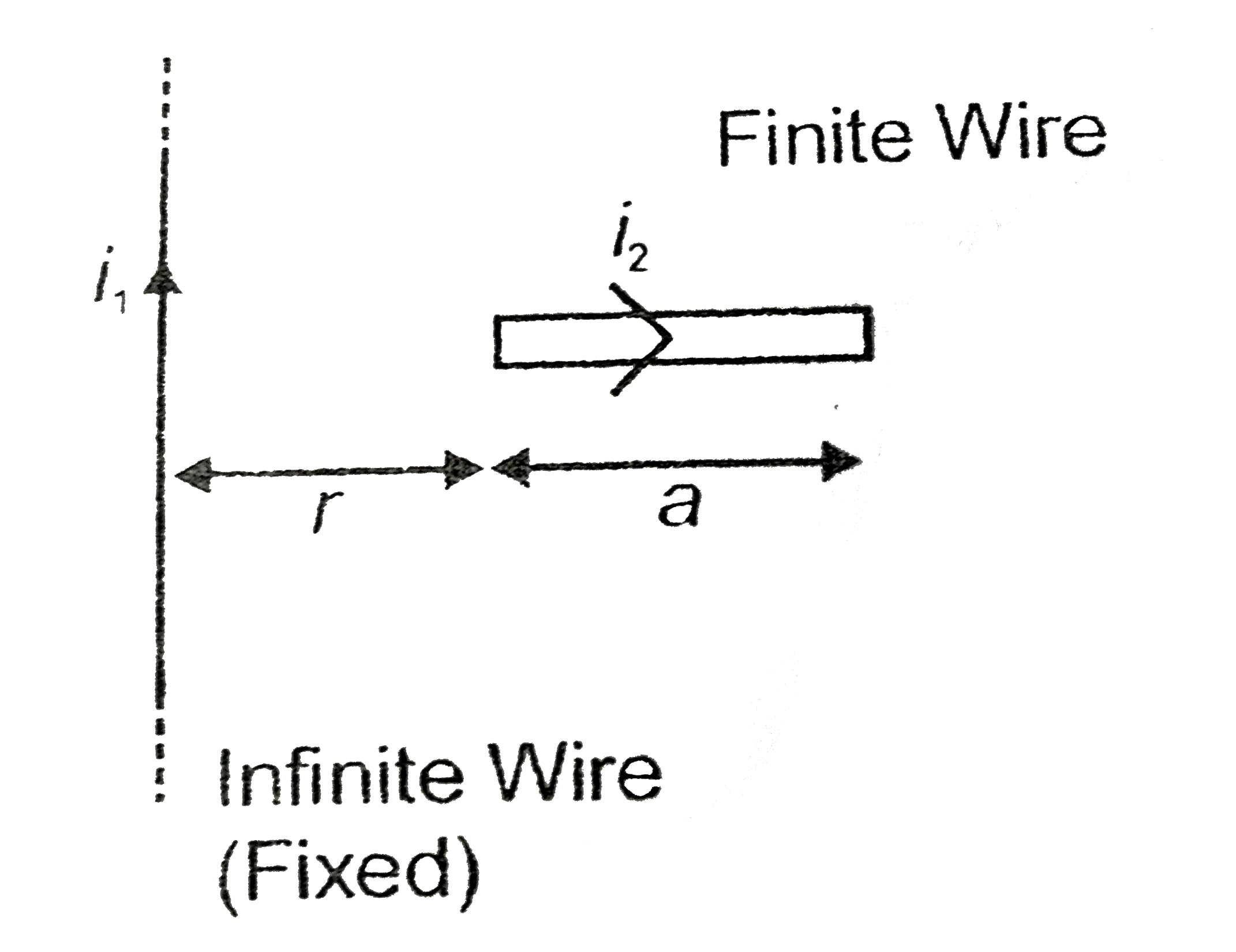
Strategy: We cannot use formula `vec(F) = i vec(l) xx vec(B)` to find the force as the magnetic field created by the fixed infinite wire is non-uniform. We have to consider an element on the finite wire, find force on it and integrate to obtain the net force.
View SolutionAn electron revolves anti-clockwise around a proton in a hydrogen atom. The speed of electron is v and radius of its circular orbit is r. find
(i) The magnetic field produced at the centre
(ii) Magnetic dipole moment of circulating electron
(iii) The ratio of magnetic moment of angular momentum of electron
Strategy: A charge in motion constitutes current. Therefore, an electron moving on circle is equivalent to a current carrying loop
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed `omega` about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA current loop of magnetic dipole moment `vec(M)` is placed in uniform magnetic field B. Initially the angle between `vec(M) and vec(B) " is " theta_(1)`. Find the work done by magnetic field as the angle is increased from `theta_(1) " to " theta_(2)`
View SolutionA coil of radius R carries a current `i_(1)`. Another concentric coil of radius `r (r lt lt R)` carries a current `i_(2)`. Planes of two coils are mutually perpendicular and both the coils are free to rotate about common diameter. Find maximum kinetic energy attained by the two coils, when both are released from rest. The masses of two coils are M and m respectively.
Strategy : The magnetic field due to coil of radius R is `(mu_(0)i_(1))/(2R)`. This field exerts a torque on shorter coil. An equal and opposite torque is exerted by the shorter coil on larger coil. There is no external torque acting on the system. The angular momentum remains conserved. Also the total mechanical energy remains conserved. At any instant, let `omega_(1) and omega_(2)` represent the angular velocity
View Solution
Example questions and complete solutions for chapter MOVING CHARGES AND MAGNETISM of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS MOVING CHARGES AND MAGNETISM
- Assignment Section C (Objective Type Questions (More than one option are correct)
- Assignment Section D (Linked Comprehension Type Questions)
- Assignment Section E (Assertion - Reason Type Questions)
- Assignment Section F (Matrix-Match Type Questions
- Assignment Section G Integer Answer Type Questions
- Assignment Section H (Multiple True-False Type Questions)
- Assignment Section I (Subjective Type Questions)
- Assignment Section J (Aakash Challengers Questions)
- Assignment (Section A) Objective Type Questions (One option is correct)
- Assignment (Section B) Objective Type Questions (One option is correct)
- Example
- Illustration
- Try Yourself