A current loop is bent in the form of a rectangule of sides a and b as shown. The current flowing through the loop is i and its direction is shown in the figure. Calculate the magnetic field at the centre of the rectangle
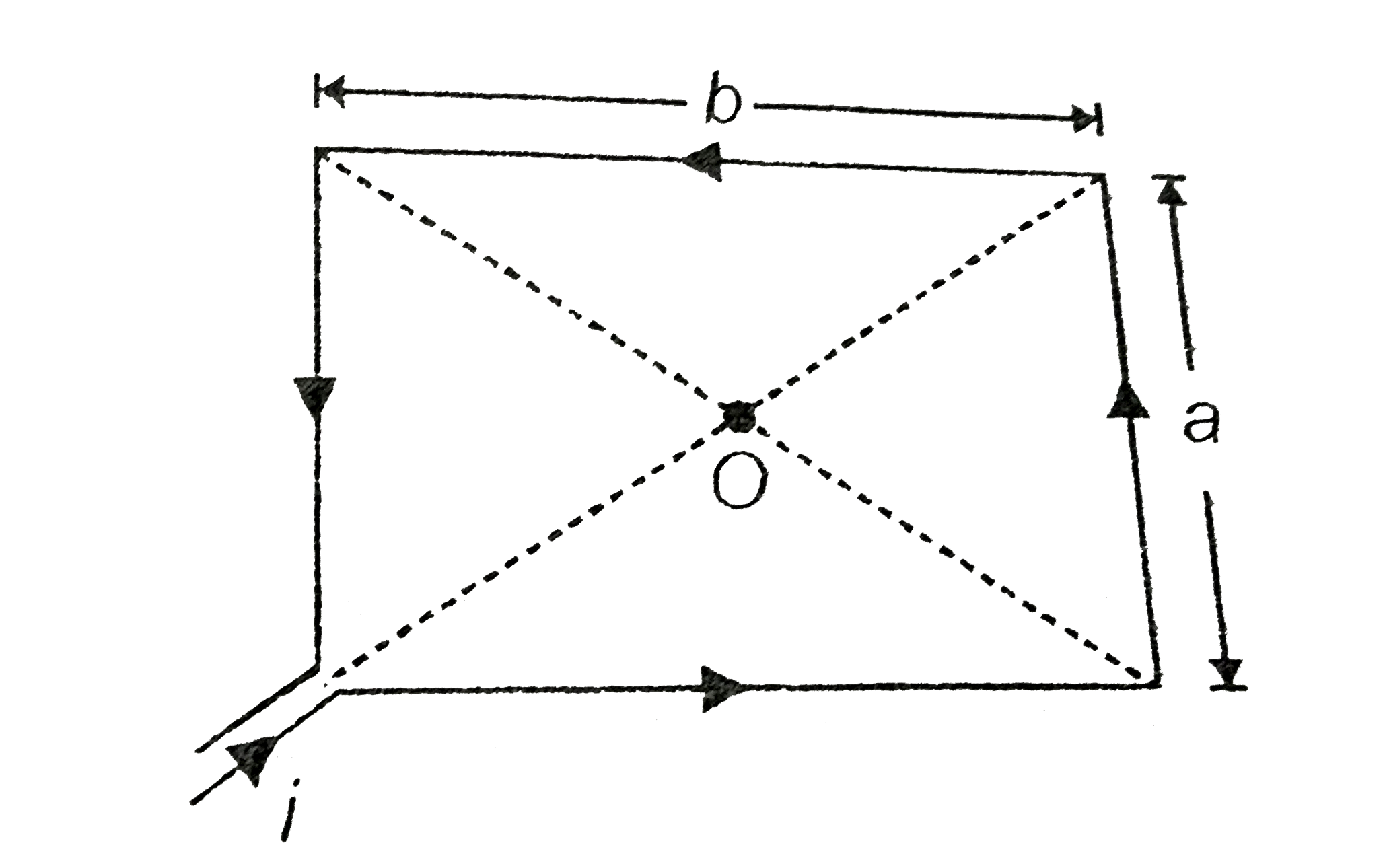
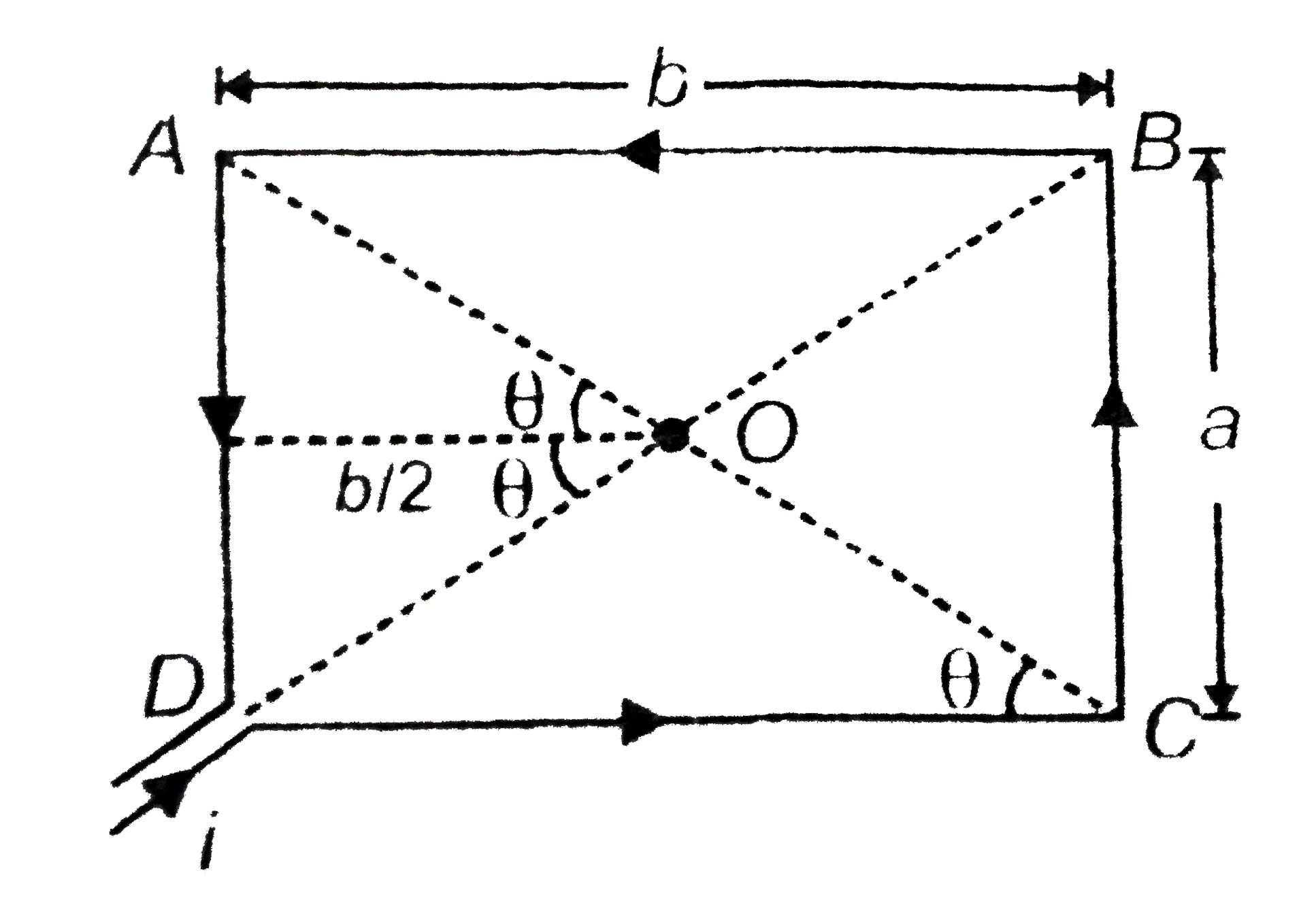
Strategy : Due to each side of the rectangle, field at O is perpendicular to the plane of paper adn outwards (you can check it using Right Hand Thumb Rule). So the fields can be added up to find net magnetic field.
Due to straight conductor AD, magnetic field is given by
BAD=μ0i4π(b/2)[sinθ+sinθ]
[Using B=μ0i4πr(sinϕ1+sinϕ2)]
As sinθ=ADAC=a√a2+b2
∴BAD=μ0iπb(a√a2+b2)
SImilarly, BAB=μ0iπa(b√a2+b2) (Hint : Interchange a and b)
BBC=μ0iπb(a√a2+b2) (same as BAD)
and BCD=μ0iπa(b√a2+b2) (same as BAB)
Net magnetic field B=BAB+BCD+BDA=2μ0iπ[ab√a2+b2+ba√a2+b2]
=2μ0iπab(√a2+b2)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Illustration
Explore 14 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGES AND MAGNETISMExercise:Try Yourself
Explore 27 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
- NUCLEIBook:AAKASH INSTITUTE ENGLISHChapter:NUCLEIExercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
Similar Questions
Find the magnetic field at the centre O of the loop shown in the figure
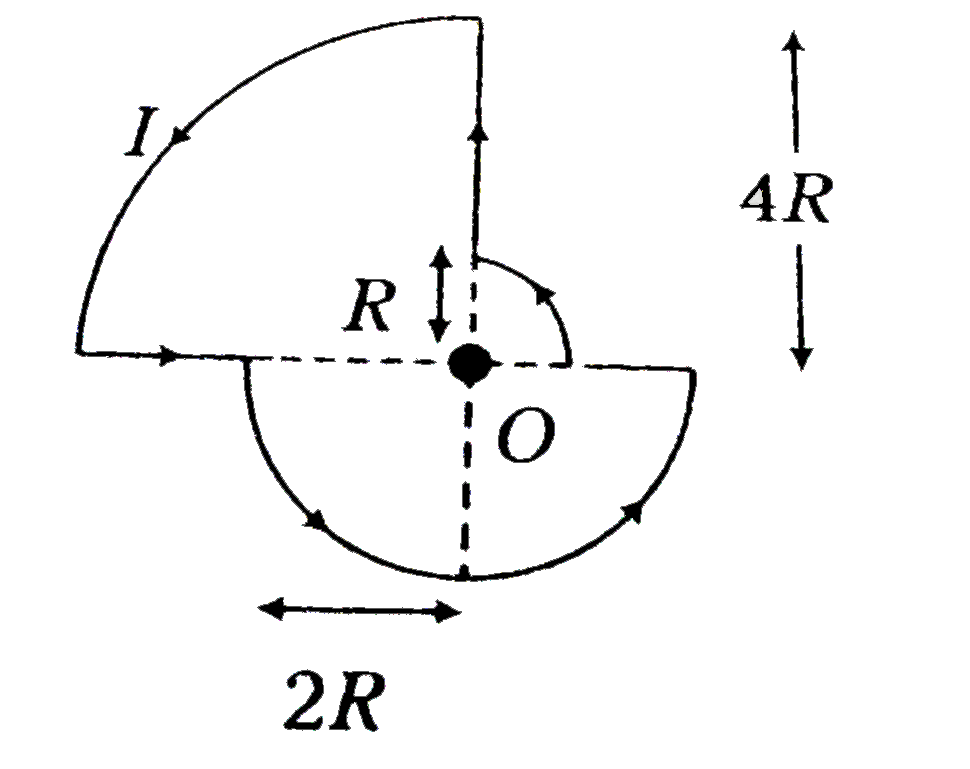
View SolutionFind the magnetic field at the centre O of the loop shown in the figure
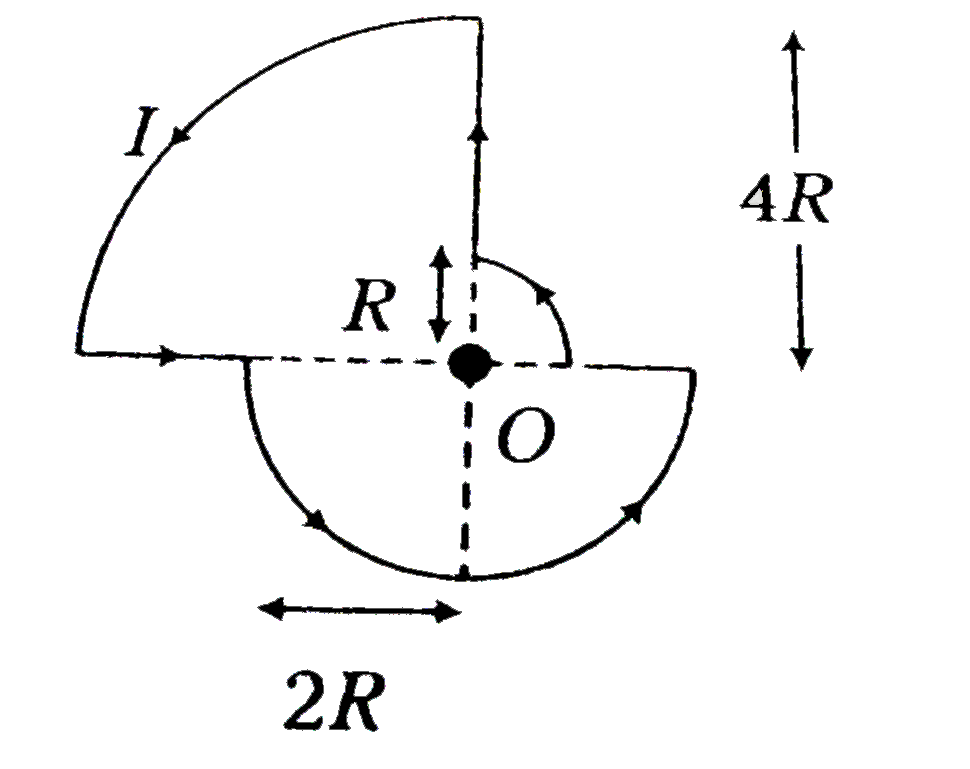
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
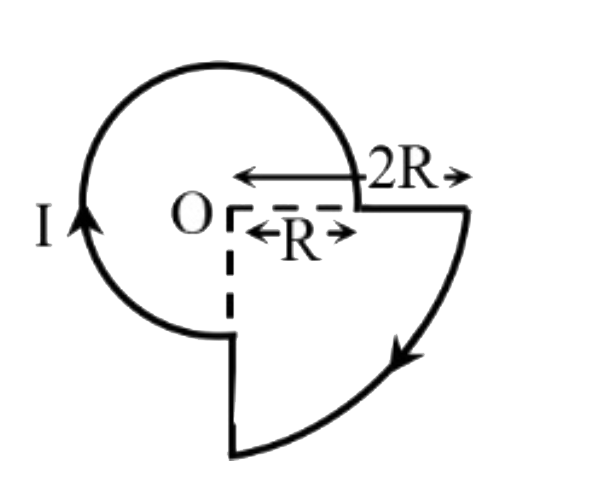
View SolutionA current of I amperes is flowing through each of the bent wires as shown. Find the magnitude of magnetic field at O.
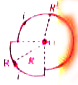
View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
View SolutionA current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
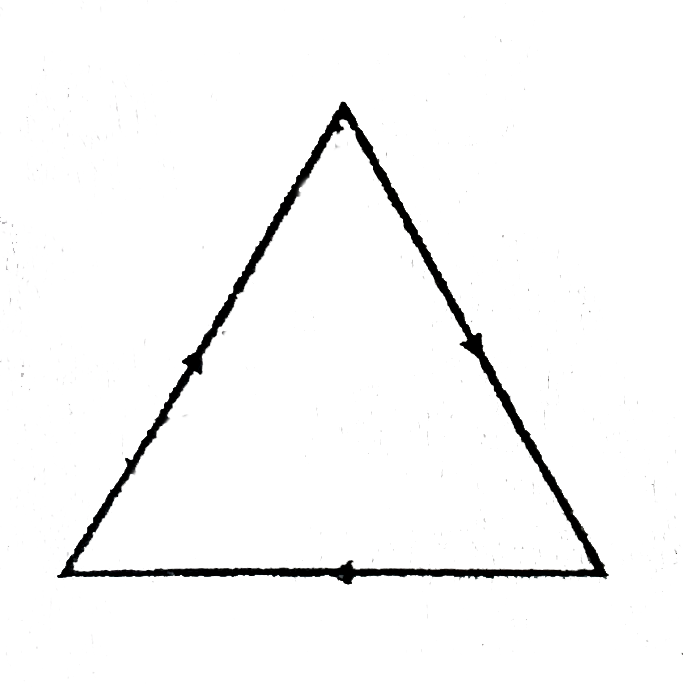
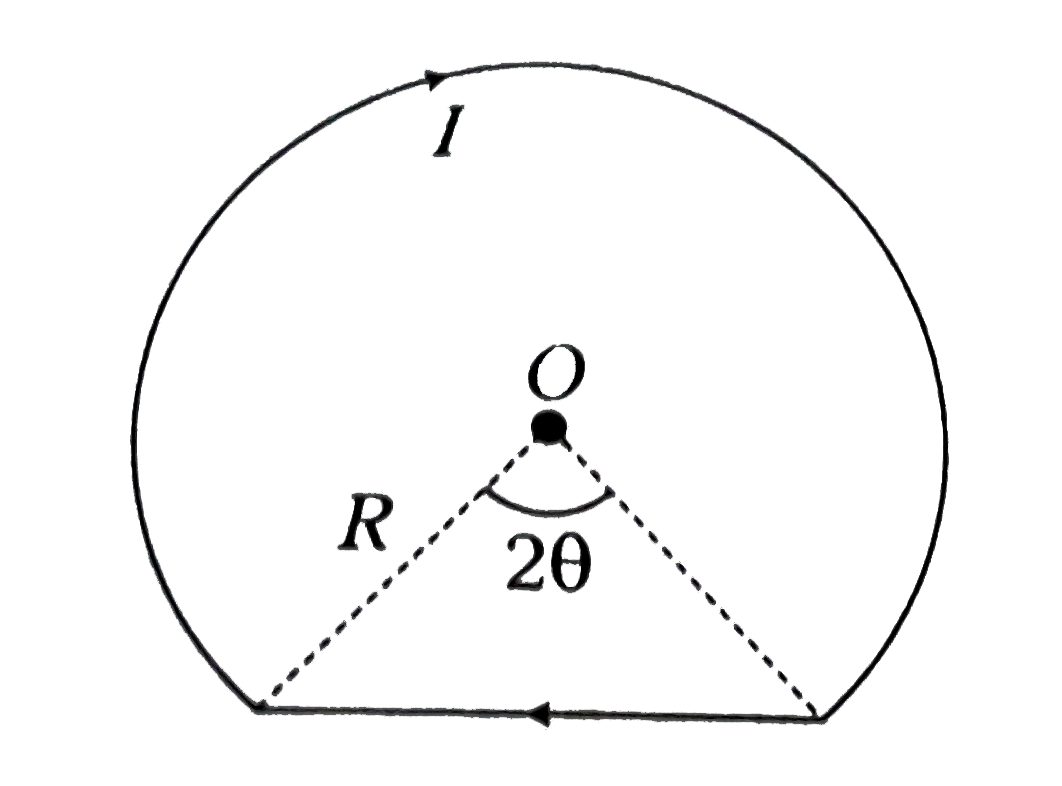
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,

View Solution
