Complete Solutions to ASSIGNMENT SECTION-J of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| AAKASH INSTITUTE | ASSIGNMENT SECTION-J |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
You have a microammeter which reads `50 muA` at full scale deflection and the coild in the meter movement has a resistance of 20 ohms. By adding two resistors , `R_(1)` and `R_(2)` and a 1.5 volt battery you can convert this into an ohmeter. When the two outcoming leads of this ohmeter are connected together , the meter is to register ohms by giving exactly full-scale deflectio. When the leads are connected across an unknown resisance R, the deflection will indicate the resistance value,if the scalse is appropriately marked . In particular , we wan half scale deflection to indicate 15 ohms. What values of `R_(1)` and `R_(2)` are required , how should the connections be made ?
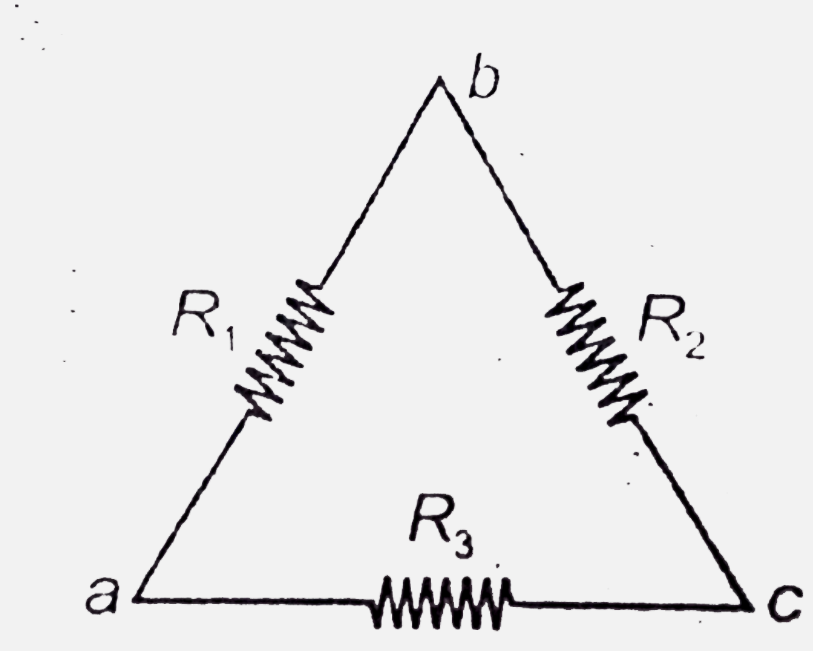
View SolutionConsider the circuit shown in the figure. Equivalent resistance between terminals ab,ac,c equals `30 Omega, 60 Omega ` and `70 Omega ` respectively. Find the respectively . Find the resistance `R_(1) , R_(2) `and `R_(3)`
View SolutionInitially switch 'S' was open and the circuit has achieved its steady state at t=0. Then , switch 'S' is sddenly closed. Find the current through resistance R as a function of time.

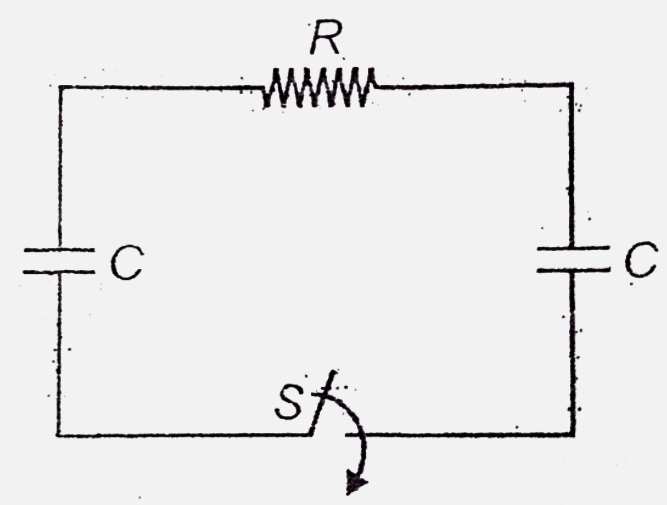
View SolutionIn the circuit shown the capacitance of each capacitance is equal to C and the resistance in R. One of the capacitance was connected to a voltage `V_(0)` and then at the moment t=0 was shorted by means of the switch S. Find
(i) Current in the circuit as a function of time.
(ii) The amount of generated heat provided a dependece l(t) is known
View SolutionTwo metal balls of the same radius a are located in a homogeneous poorly conducting meium with resistivity `rho`. Find the resistance of the medium between the balls provided that the separated between them is much greater than the radius of the ball.
Strategy `:` Let us mentally impart the charge `+q` and `=q` to the balls respectively. The electric field strength at the surface of a ball will be determined only by its own charge and the cahrge can be considered to be uniformly distributed over the surface, because the other ball is at infinite distance.
View SolutionA rod of length `L` and cross-section area `A` lies along the x-axis between `x=0` and `x=L`. The material obeys Ohm's law and its resistivity varies along the rod according to `rho(x) = rho_0 epsilon^(-x//L)`. The end of the rod `x=0` is at a potential `V_0` and it is zero at `x=L`.
(a) Find the total resistance of the rod and the current in the wire.
(b) Find the electric potential in the rod as a function of `x`.
View SolutionIf all the energy lost from joule heating stays in a wire , and the temperature increases as a result the resistivity also increase. The current will therefore change as a function of time of time, the joule heating will change and so forth. If the wire material has constant heat capacity , the rate of energy loss in wire will be proportional to rate of change of temperature . Assuming that potential stays constant set up a differential equation that describes the rate of change of temperature .If this equation is solved, how can the current he found as a function of time ?
(Given m is the mass of the wire , V is the potential difference across the wire, C is the specfic heat capacity of wire , `alpha` is the thermal coefficient of resistance, `R_(0)` is the resistance of wire at initial temperature `T_(0))`.
View SolutionIn a uniform solid cylinder of radius R conductivity increases linearly with the distance as we move from the axis to the surface of cylinder from `sigma_(1)` to `sigma_(2)`. Current I enters the cylinder from one end and leaves from the other end. Find the current density as a function of distance from axis of the cylinder at any cross-section.

View SolutionConsider
` .
.
The charge appearing is `C_(2)` is.
View Solution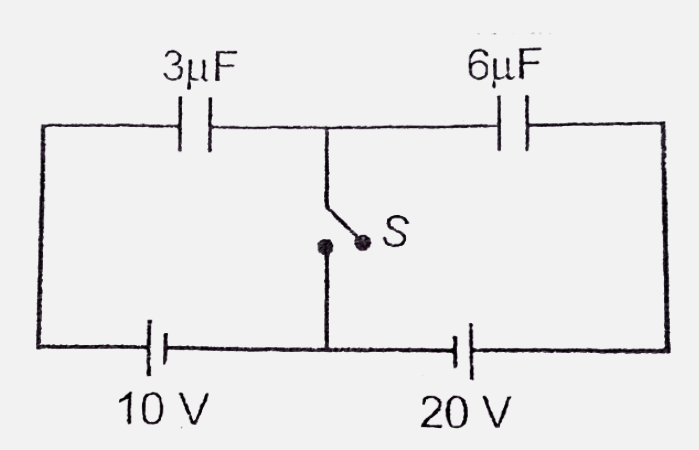
At t=0 switch S is closed . Find
(i) Charge flown through switch
(ii) Charges flown through both cells.
(iii) Work done by both cells
(iv) Heat dissipated in circuit.
View Solution
ASSIGNMENT SECTION-J questions and complete solutions for chapter CURRENT ELECTRICITY of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS CURRENT ELECTRICITY
- ASSIGNMENT SECTION-I(SUBJECTIVE TYPE QUESTIONS)
- ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
- ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
- ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS)
- ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS) Comprehension - II
- ASSIGNMENT SECTION-E (ASSERTION-REASON TYPE QUESTION)
- ASSIGNMENT SECTION-H ( MULTIPLE TRUE-FALE TYPE QUESTIONS)
- ASSIGNMENT SECTION-H( INTEGER ANSWER TYPE QUESTIONS)
- ASSIGNMENT SECTION-J
- ASSIGNMENT SECTION-J(MATRIX-MATCH TYPE QUESTIONS)
- ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
- EXAMPLE
- Try Yourself