Complete Solutions to Exercise (More Than One Correct Option Type Questions) of chapter DIFFERENTIATION of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | DIFFERENTIATION |
| ARIHANT MATHS | Exercise (More Than One Correct Option Type Questions) |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
If `y=(secx-tanx)/(secx+tanx),` then `(dy)/(dx)` equals.
View SolutionIf `y=(x^4+x^2+1)/(x^2+x+1)` then `(dy)/(dx)=a x+b` , find `a` and `b`
View SolutionWhich of the following could be the sketch graph of `y = (d(xlnx))/dx`
View SolutionLet `f(x)=x+3ln(x-2)&g(x)=x+5ln(x-1),` then the set of `x` satisfying the inequality `f^(prime)(x)
View SolutionIf ` cos^(-1) ((x^(2) -y^(2))/( x^(2)+y^(2)))=a ,then (dy)/(dx) =`
View SolutionIf`f(x)=|x|^(|sinx|)`,then`f'((pi)/(4))` equals
View Solution`y=x/(a+x/(b+x/(a+x/(b+...oo))))`, `(dy)/(dx)=b/(a(b+2y))`
View SolutionIf `y=x^(x^(2)),` then `(dy)/(dx)` equals
View Solution`"If "xsqrt(1+y)+ysqrt(1+x)=0," prove that "(dy)/(dx)=-(1)/((x+1)^(2)).`
View SolutionIf `x^2e^y+2xye^x+13=0` then `(dy)/(dx)=`
View SolutionIf `x=e^(y+e^(y+e^(y+...oo))),xgt0`, then `(dy)/(dx)` is equal to
View SolutionLet `g` be the inverse function of `f and f'(x)=(x^(10))/(1+x^(2)).` If `g(2)=a` then `g'(2)` is equal to
View SolutionIf `f and g` are the function whose graphs are as shown, let `u(x)=f(g(x)),w(x)=g(g(x))`
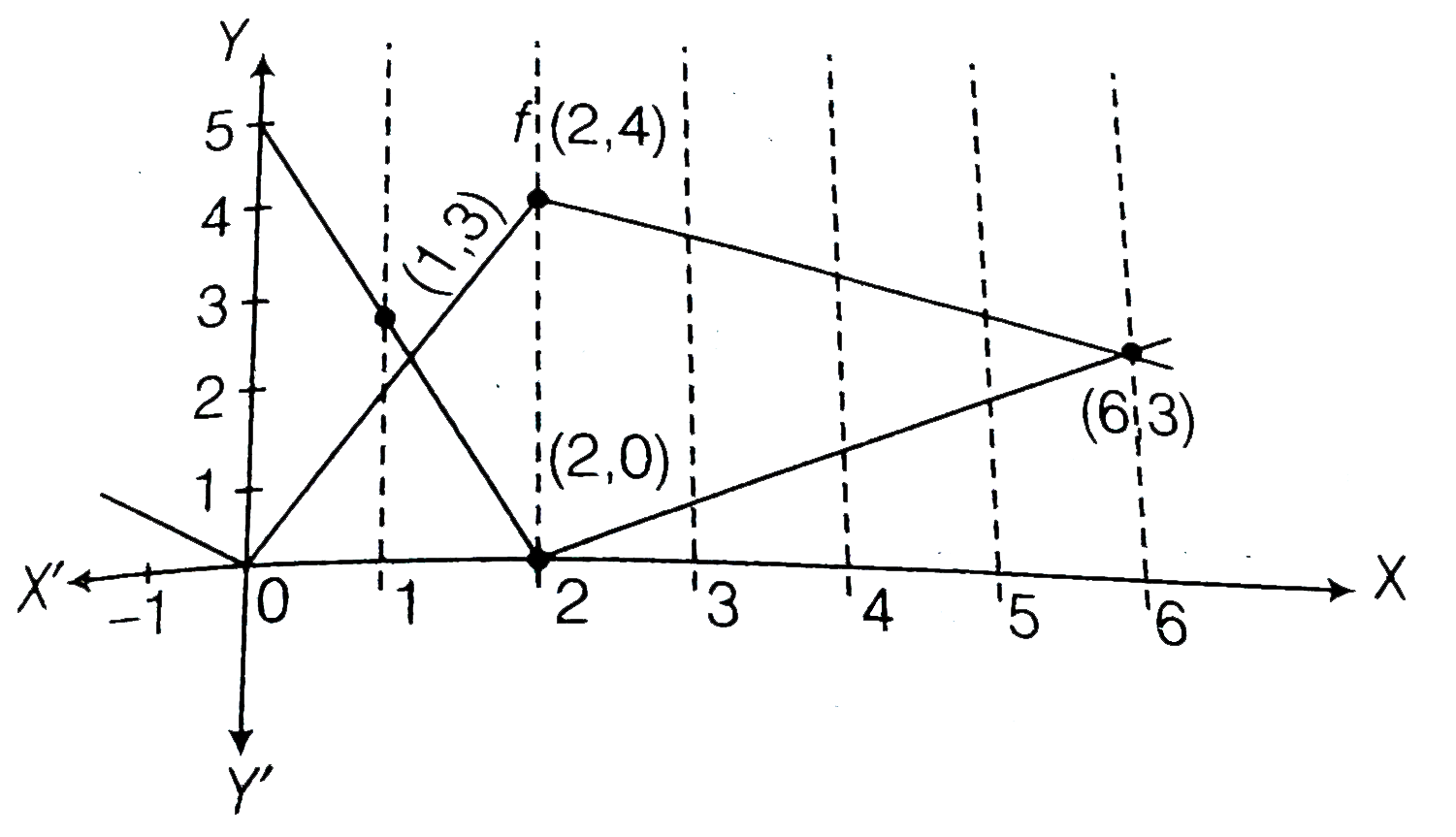 Then the value of `u'(1)+w'(1)` is
Then the value of `u'(1)+w'(1)` is
View Solution`f'(x) = g(x) and g'(x) =-f(x)` for all real x and `f(5)=2=f'(5) then f^2 (10) + g^2 (10)` is
View SolutionIf `y=(f_(0)f_(0)f)(x)andf(0)=0,f'(0)=2` then `y'(0)` is equal to
View SolutionIf `y^2=P(x)` is a polynomial of degree `3,` then `2(d/(dx))(y^2dot(d^2y)/(dx^2))` is equal to `P^(x)+P^(prime)(x)` (b) `P^(x)dotP^(x)` `P(x)dotP^(x)` (d) a constant
View SolutionIf `y=f(x)andx=g(y)` are inverse functions of each other, then
View SolutionIf `y` is a function of `x` then `(d^2y)/(dx^2)+y \ dy/dx=0.` If `x` is a function of `y` then the equation becomes
View SolutionLeg `g(x)=ln(f(x)),` whre `f(x)` is a twice differentiable positive function on `(0,oo)` such that `f(x+1)=xf(x)dot` Then, for `N=1,2,3,` `g^(N+1/2)-g^(1/2)=`
View SolutionIf the functions `f(x)=x^(3)+e^(x//2) " and " g(x)=f^(-1)(x)`, the value of g'(1) is ………… .
View SolutionLet `f(theta)=sin(tan^(-1)((sintheta)/(sqrt(cos2theta))))`, where `-pi/4ltthetaltpi /4`then the value of `d/ (d(tantheta)) f(theta)`is
View SolutionIf `y=log_(sinx)(tanx),` then `(dy)/ (dx)` at `x=(1)/(4)` is equal to
View SolutionIf `y=sum_(r=1)^(x) tan^(-1)((1)/(1+r+r^(2)))`, then `(dy)/(dx)` is equal to
View SolutionIf `y=(sin^(-1)(sinalphasinx)/(1-cosalphasinx))`, then `y'(0)` is equal to
View SolutionIf `f(x)=cot^(-1)((x^(x)-x^(-x))/(2))` then f'(1) equals
View SolutionThe function `f(x)=e^x+x ,` being differentiable and one-to-one, has a differentiable inverse `f^(-1)(x)dot` The value of `d/(dx)(f^(-1))` at the point `f(log2)` is `1/(1n2)` (b) `1/3` (c) `1/4` (d) none of these
View SolutionIf `f''(x)=-f(x) and g(x)=f^(prime)(x)` and `F(x)=(f(x/2))^2+(g(x/2))^2` and given that `F(5)=5,` then `F(10)` is (a)5 (b) 10 (c) 0 (d) 15
View Solutionabout to only mathematics
View SolutionIf `x=f(t)cost-f^(prime)(t)sint` and `y=f(t)sint+f^(prime)(t)cost ,` then `((dx)/(dt))^2+((dy)/(dt))^2=` `f(t)-f"(t)` (b) `{f(t)-f"(t)}^2` (c) `{f(t)+f"(t)}^2` (d) none of these
View SolutionIf `y=at^2+2bt-c`and ` t = ax^2+2bx+c`, then`(d^3y)/(dx^3)` equals
View SolutionDifferential coefficient of `(x^((l+m)/(m-n)))^(1//(n-l))*(x^((m+n)/(n-l)))^(1//(l-m))*(x^((n+l)/(l-m)))^(1//(m-n))` wrt `x` is
View Solutionif `y=(A+Bx)e^(mx)+(m-1)^-1 e^x` then `(d^2y)/(dx^2)-2m(dy)/(dx)+m^2y` is equal to:
View SolutionIf `f(x)=cos^(-1)1/(sqrt(13))(2cosx-3sinx)` `+sin^(-1)1/(sqrt(13))x(2cosx+3sinx)wdotrdottsqrt(1+x^2),` then find `(df(x))/(dx)` at `x=3/4dot`
View SolutionIf `f(x)=sqrt(x+2sqrt(2x-4))+sqrt(x-2sqrt(2x-4))` then the value of 10 `f'(102^(+))`, is
View SolutionLet `y=1n(1+cosx)^2` . Then the value of `(d^2y)/(dx^2)+2/(e^(y/2))` equal (b) `2/(1+cosx)` `4/(1+cosx)` (d) `(-4)/((1+cos"x")^2)`
View SolutionIf `f(x)=(a+sqrt(a^2-x^2)+x)/(sqrt(a^2-x^2)+a-x)` where `a>0` then `f'(0)` has the value equal to
View SolutionLet `u/x a n dv(x)` be differentiable functions such that `(u(x))/(v(x))=7.If(u^(prime)(x))/(v^(prime)(x))=pa n d((u(x))/(v(x)))=q ,t h e n(p+q)/(p-q)` has the value of to 1 (b) 0 (c) 7 (d) `-7`
View SolutionIf f(x) `=|log_(e)|x||,` then f'(x) equals
View SolutionIf `f(x)` is given by
`f(x)=(cosx+i sinx)(cos3x+isin3x)`.........
.......`[cos(2n-1)x+isin(2n-1)x]`,
then f''(x) is equal to
View SolutionLet `f(x)=x^(n)` , n being a non-negative integer, The value of `n` for which the equality `f'(x+y)=f'(x)+f'(y)` is valid for all `x,ygt0,` is
View SolutionIf `f(x)=sin{(pi)/(3)[x]-x^(2)}" for "2ltxlt3` and [x] denotes the greatest integer less than or equal to x, then `f'"("sqrt(pi//3)")"` is equal to
View SolutionThe function `u=e^x sin x ; v=e^x cos x` satisfy the equation a.`v(d u)/(dx)-u(d v)/(dx)=u^2+v^2` b. `(d^2u)/(dx^2)=2v` c. `(d^2v)/(dx^2)=-2u` d. `(d u)/(dx)+(d v)/(dx)=2v`
View SolutionIf `f(x)=log_(x^(2))(logx)`,then f '(x)at x= e is
View SolutionLet f be a differentiable function satisfying
`[f(x)]^(n)=f(nx)" for all "x inR.`
Then, `f'(x)f(nx)`
View SolutionIf `y=f(x)` is an odd differentiable function defined on `(-oo,oo)` such that `f^(prime)(3)=-2,t h e n|f^(prime)(-3)|` equals_________.
View Solution`"If "y=sqrt(x+sqrt(y+sqrt(x+sqrt(y+...oo))))," then prove that "(dy)/(dx)=(y^(2)-x)/(2y^(3)-2xy-1)`
View SolutionIf `f(x)=|cosx-sinx| `, then `f'(pi/4)` is equal to
View SolutionLet `f(x)=x^2+xg^2(1)+g^''(2) and g(x)=f(1).x^2+xf'(x)+f''(x),` then find `f(x) and g(x).`
View Solutionif `f(x) = x^n` then the value of `f(1) - (f'(1))/(1!) + (f''(1))/(2!) + ---+((-1)^n f''^--n times (1))/(n!)`
View SolutionIf `y+log(1+x)=0` which of the following is true?
View SolutionIf `y=2^(3^(x))`, then `y'` equals
View SolutionIf `g` is the inverse of `fandf(x) = x^(2)+3x-3,(xgt0).` then `g'(1)` equals
View SolutionIf `x^(3)-2x^(2)y^(2)+5x+y-5=0 and y(1) = 1`, then
View SolutionLet `y=sqrt(x+sqrt(x+sqrt(x+oo)))` , `(dy)/(dx)` is equal to
(a)`1/(2y-1)` (b) `x/(x+2y)` (c)`1/(sqrt(1+4x)` (d) `y/(2x+y)`
View SolutionIf`y=x^((lnx)^ln(lnx))` , then `(dy)/(dx)` is equal to
View SolutionWhich of the following functions are not derivable at `x=0?`
View Solution`"Let "f(x)=(sqrt(x-2sqrt(x-1)))/(sqrt(x-1-1))x." Then"`
View SolutionIf `2^(x)+2^(y)=2^(x+y)` then `(dy)/(dx)`is equal to
View SolutionFor the function `y=f(x)=(x^(2)+bx+c)e^(x)`, which of the following holds?
View SolutionIf `sqrt(y+x)+sqrt(y-x)=c,` where `cne0`, then `(dy)/(dx)` has the value equal to
View SolutionIf `y = tan x tan 2x tan 3x, (sin 12x != 0)` then `dy / dx` has the value equal to
View Solution
Exercise (More Than One Correct Option Type Questions) questions and complete solutions for chapter DIFFERENTIATION of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS DIFFERENTIATION
- Differentiation Exercise 5:
- EXAMPLE
- Examples
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 10
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 3:
- Exercise For Session 4
- Exercise For Session 5
- Exercise For Session 6
- Exercise For Session 7
- Exercise For Session 8
- Exercise For Session 9
- SOLVED EXAMPLES