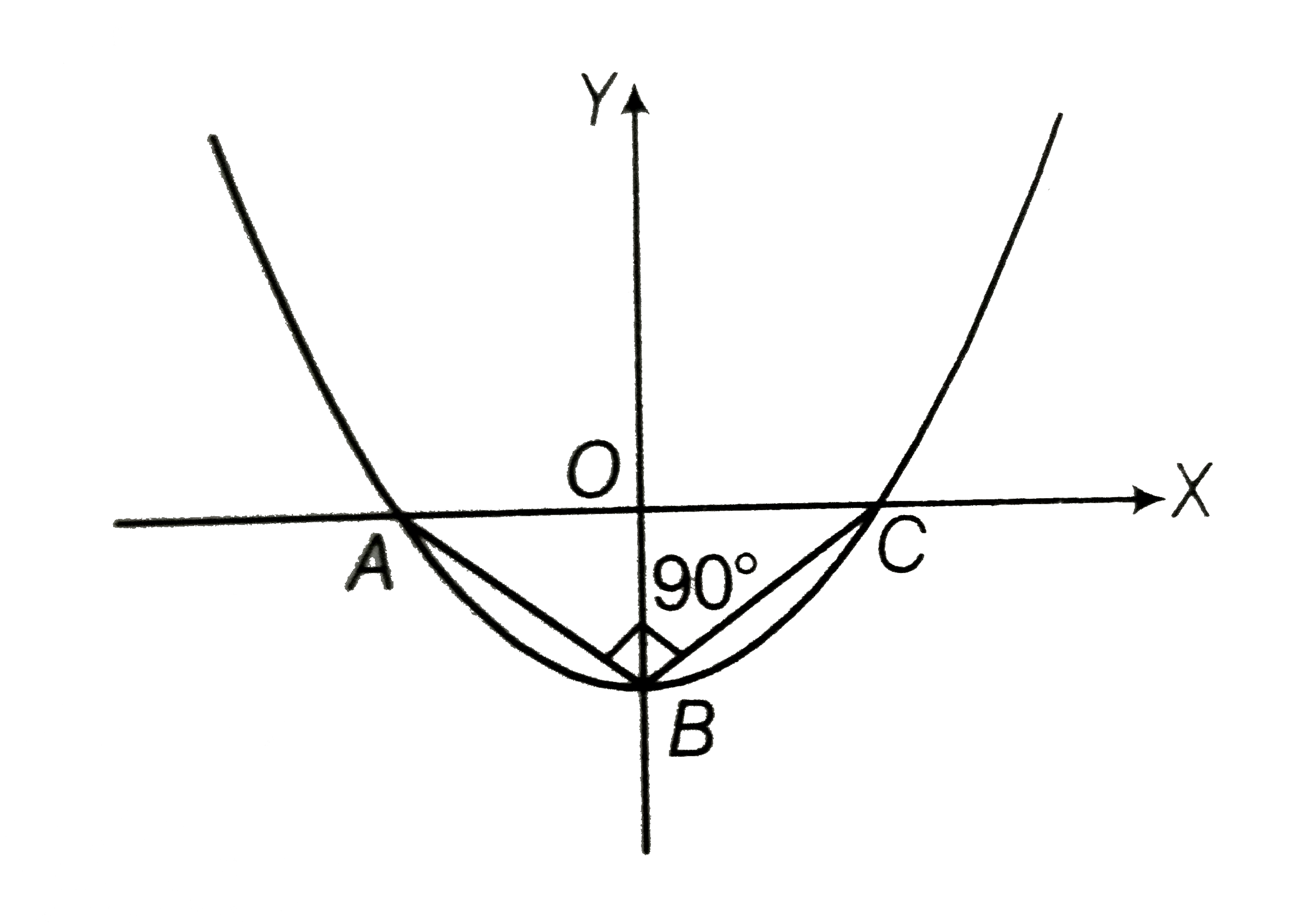
In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.
y=f(x) is given by
y=−x2−8
y=x22√2−2√2
y=x2−4
y=x22−√2
The correct Answer is:B
Given that AC=4√2 units
∴AB=BC=AC√2=4 units andd OB=√(BC)2−(OC)2
=√(4)2−(2√2)2[∵OC=AC2]
=2√2 units
∴ Vertices are A=(−2√2,0),
B=−(0,−2√2)
and C=(2√2,0)
Since y=f(x)=ax2+bx+c passes through A,B and C then
0=8a−2√2b+c−2√2=c
and 0=8a+2√2b+c
We get b=0,a=12√20 and c=−2√2
∴y=f(x)=x22√2−2√2
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:ARIHANT MATHS ENGLISHChapter:THEORY OF EQUATIONSExercise:Exercise (Single Integer Answer Type Questions)
Explore 10 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHS ENGLISHChapter:THEORY OF EQUATIONSExercise:Exercise (Matching Type Questions)
Explore 2 Videos
- THEORY OF EQUATIONSBook:ARIHANT MATHS ENGLISHChapter:THEORY OF EQUATIONSExercise:Exercise (More Than One Correct Option Type Questions)
Explore 15 Videos
- THE STRAIGHT LINESBook:ARIHANT MATHS ENGLISHChapter:THE STRAIGHT LINESExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 17 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBook:ARIHANT MATHS ENGLISHChapter:THREE DIMENSIONAL COORDINATE SYSTEMExercise:Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
Explore 2 Videos
Similar Questions
In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.
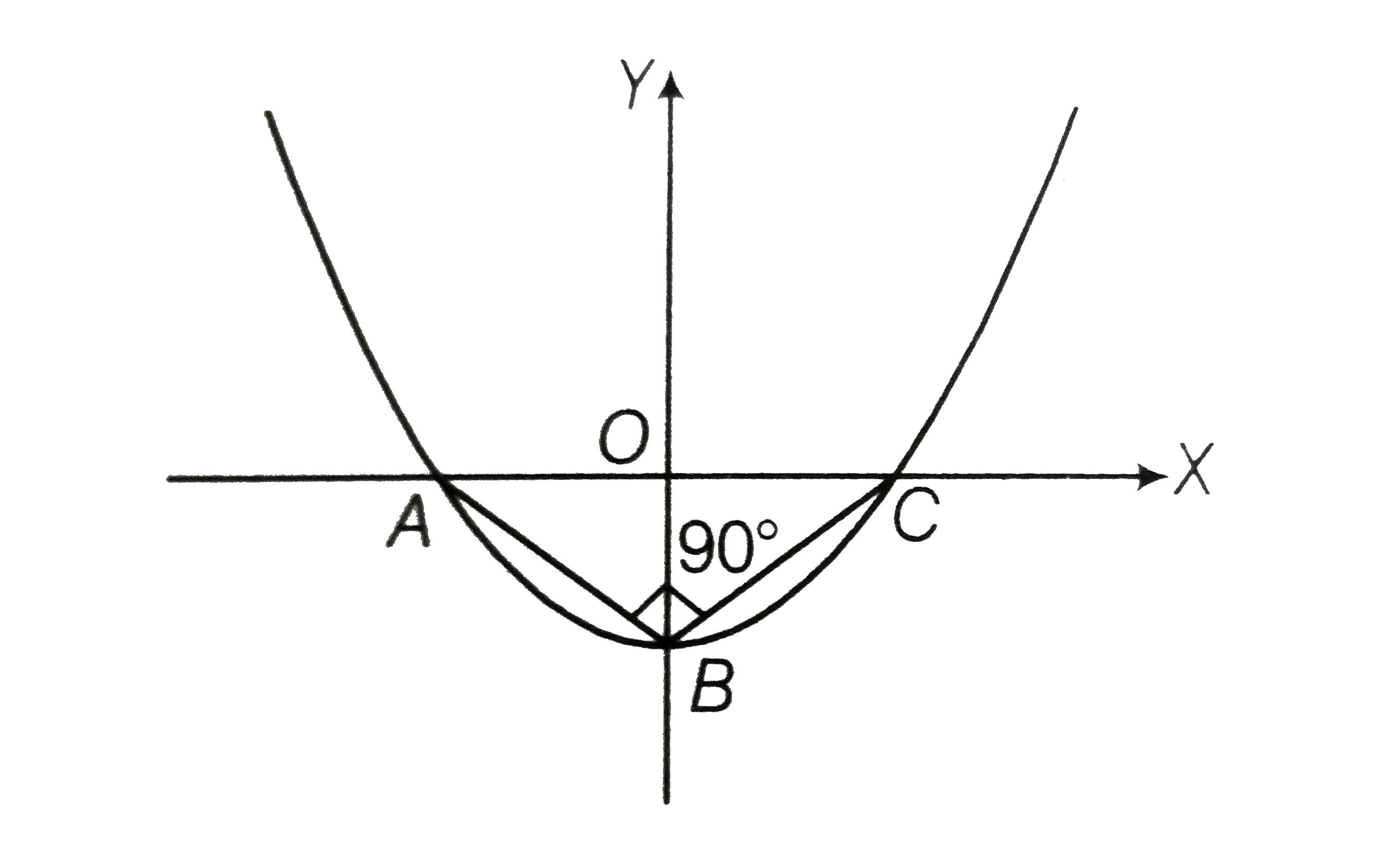
Minimum valueof y=f(x) is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
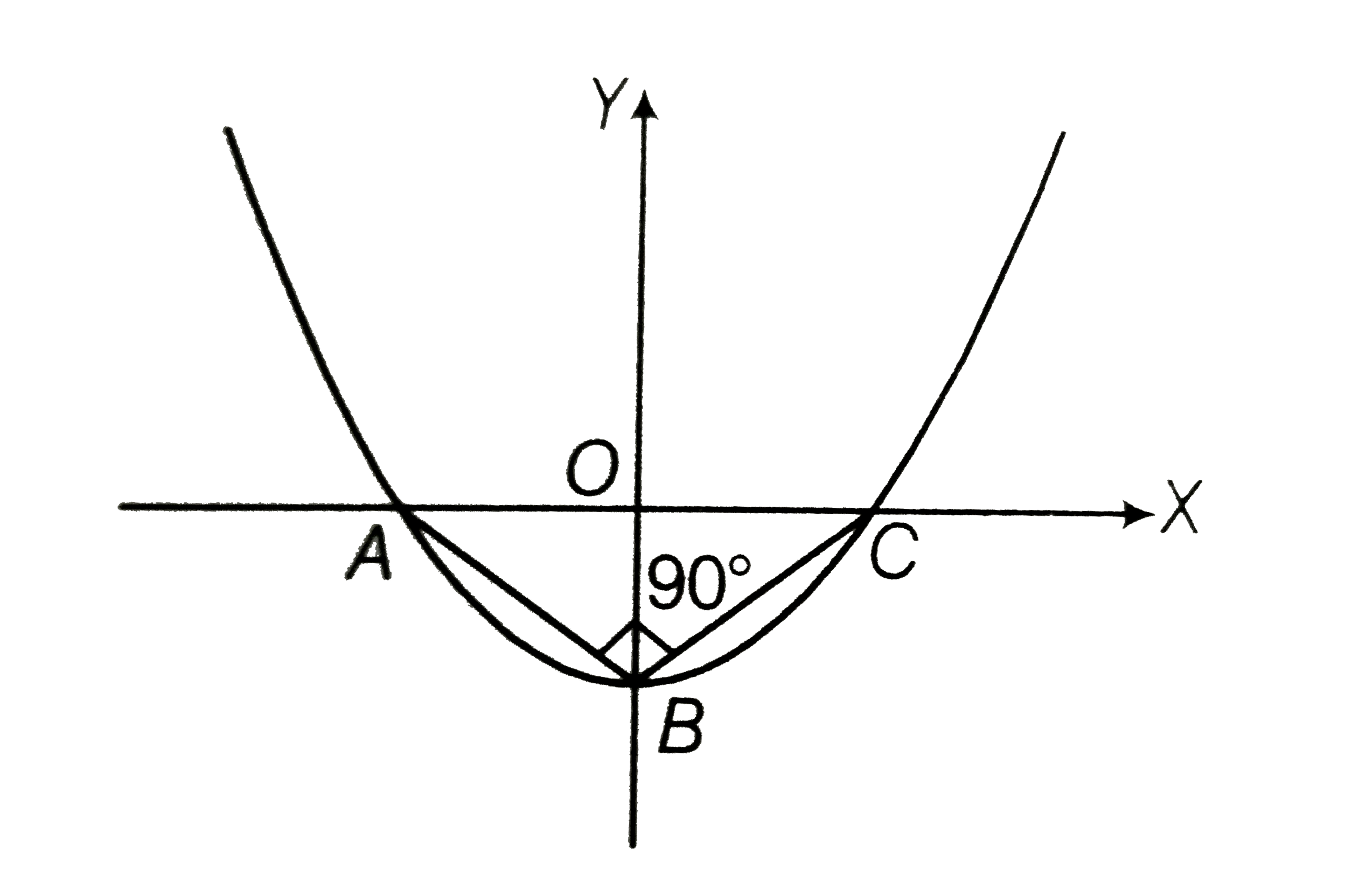
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View SolutionDraw a right angled isosceles triangle whose hypotenuse is 5.2 cm long.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionThe length of the hypotenuse of an isosceles right triangle whose one side is 4√2 cm is 12cm (b) 8cm (c) 8√2cm (d) 12√2cm
View SolutionA right angled isosceles triangle is inscribed in the circle x2+y2_4x−2y−4=0 then length of its side is
View SolutionFind the equations of the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as
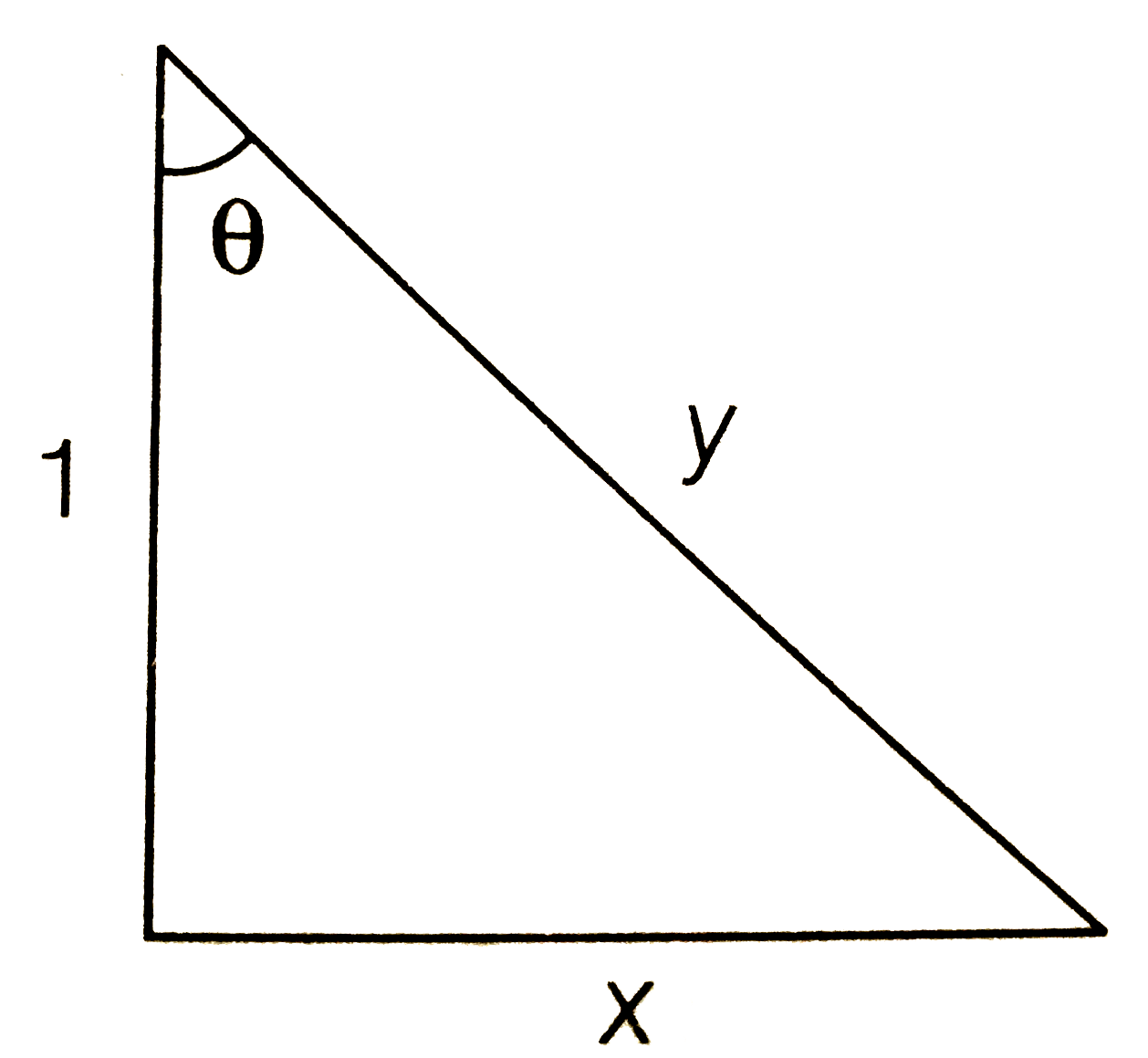

View SolutionFind the equations the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
View SolutionFind the equation of one of the side of an isosecles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2,2).
View Solution