Complete Solutions to Practice Exercise of chapter FLUID MECHANICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | FLUID MECHANICS |
| BITSAT GUIDE | Practice Exercise |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
The pressure at the bottom of a tank of liquid is not proprtional to
View SolutionIf a vessel containing a fluid of density `rho` upto height h is accelerated vertically downwards with accelerations `a_(0)`. Then the pressure by fluid at the bottom of a vessel is
View SolutionIn each heart beat, a heart pumps 80 ml blood at an average pressure of 100 ml of Hg. What will be the power output of the herat? (Assume 60 heart beat per minute
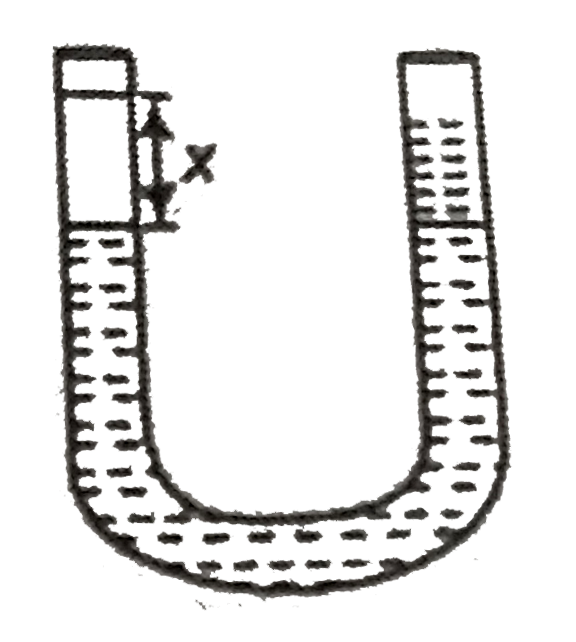
View SolutionOne end a U-tube of unifrom bore (area A) cpmtaining mercury is connected to sunction pump . Because of it the level of liquid of density `rho` falls in one limb. When the pump is removed, the restoring force in the other limb is
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity `omega` then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionIf the weight of a body in vacuum is w and `w_(1)` and `w_(2)` are weights when it is immersed in a liquid of specific gravity `rho_(1)` and `rho_(2)` respectively, then find the relation among `w,w_(1)and w_(2)`
View SolutionA closed rectangular tank 10 m long, 5 m, wide and 3 m deep is completely filled with and oil of specific gravity `0.92` . Find the preesure difference betweenn the nrear and front cornrers of the tank, if is moving with an acceleration of `3 m//s^(2)` in the horizontal direction
View SolutionA U-tube having a liquid of density `rho` is accelerated at a `m//s^(2)` , so as to create be the height difference between two columns of l/2 (as shown if figure) . If/is the length of the base of U-tube the value of acceleration given to the system is

View SolutionA body weight 5 N in air and 2 N when immersed in a liquid. The buoyant force is
View SolutionA necless weighing 50 g in air, but it weight 46 g in water. Assume copper is mixed with gold to prepare the neckless. Find how much copper is present in it. (Specific gravity of gold is 20 and that of copper is 10 )
View SolutionIf air of weight w is filled in a empty ballon which weights `w_(1)` the weight of ballon will become `w_(2)` Suppose the density of air inside and out side the vallon is same, then,
View SolutionA soft plastic bag of weight `w_(0)` is filled with air at STP Now, weigth of the bag is w in air. Then,
View SolutionA block of ice of area A and thickness `0.5 m` is floating in the fresh water. In order to just support a man of 100 kg , the area A should be (specific gravity of ice `0.917` and density of water `=1000 kg//m^(2))`
View SolutionA pieceo of ice is floating in water . Find the fraction of volume of he piece of ice outside the water
(Given density of ice `=900 kg//m^(3)` and density of water `=1000 kg//m^(3))`
View SolutionA block of wood floats with 1//4 of its volume under water. What is he density of wood? (Density of water `=1000 kg //m^(3))`
View SolutionA block weights 15 N and 12 N in air and water respectively . When it is immeresed in another liquid, it weights 13 N then find the relative density of ice is block.
View SolutionIn English the phrase tip of the iceberg is used to mean a small visible fraction of something that is mostly hidden . For a real iceberg. What is this fraction. If the density of sea water is `1.03 kg//c c` and that of ice is `0.92 g//c c`?m
View SolutionVessel contains oil `(density 0.8 g//c c)` over mercury (density `13.6 g//c c)` A homogeneous sphere floats with half its volume immersed in mercury and the other half in oil. The density of the sphere in g/c c is
View SolutionIn a steady icnompressible flwo of a liquid
View SolutionWater from a tap emerges vertically downwards an intial speed of 1 m/s . The cross-sectional area of the tap is `10^(-4)m^(2)` . Assume that the pressure is contant throughout the stream of water and that the flow is steady . The cross-sectional area of the steam. `0.15` m below the tap is
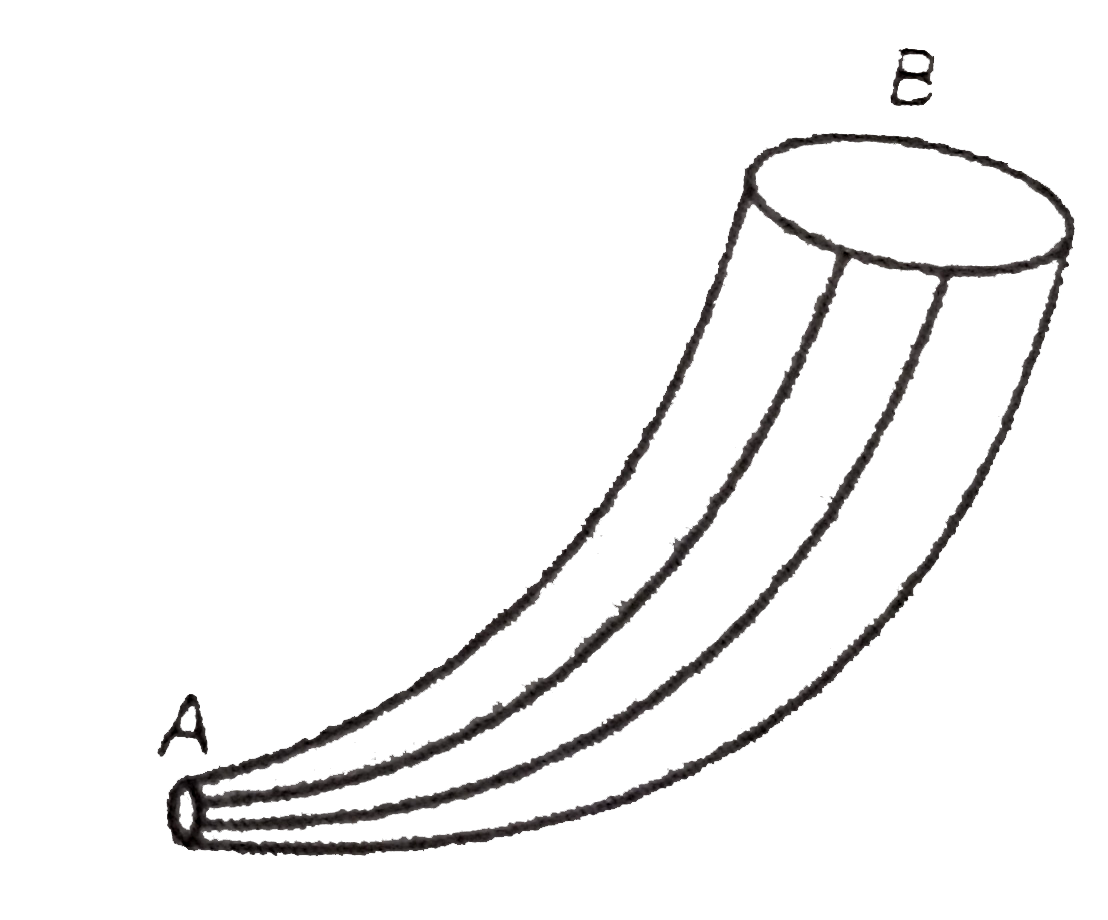
View SolutionA tube of flow is shown in the figure.
View SolutionA pipe GB is fitted withb two pipes C and D as shown in the figure. `A=24 m^(2)` at G and velocity of water at G is 10 m/s and at C is 6 m/s . The velocity of water at D is

View SolutionBernoulli's equation is applicable to points
View SolutionThe horizontal flow of fluid depends upon
View Solutionin steday horizontal flow,
View SolutionFrom a horizontal tube with area of cross-section `A_(1)` and `A_(2)` as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.

View SolutionA vessel is filled with water and kerosence oil. The vessel has a small hole in the bottom. Neglecting viscosity if the thickness of water layer is `h_(1)` and kerosens layer is `h_(2)` then the velocity v of flow of water will be (density of water is `rho_(1)`b g/c c and that of kerosense is `rho_(2)` g/c c
View SolutionMark the correct options (s).
View SolutionWater flows along horizontal pipe whose cross-section is not constant. The pressure is 1 cm of Hg, where the veloecity is 35 cm/s . At a point where the velocity is 65cm/s then pressure will be
View SolutionA pilot tube was inserted in a pipe to measure the velocity of water in it. If the water rises in the tube is 200 mm . Find the velocity of water.
View SolutionA cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
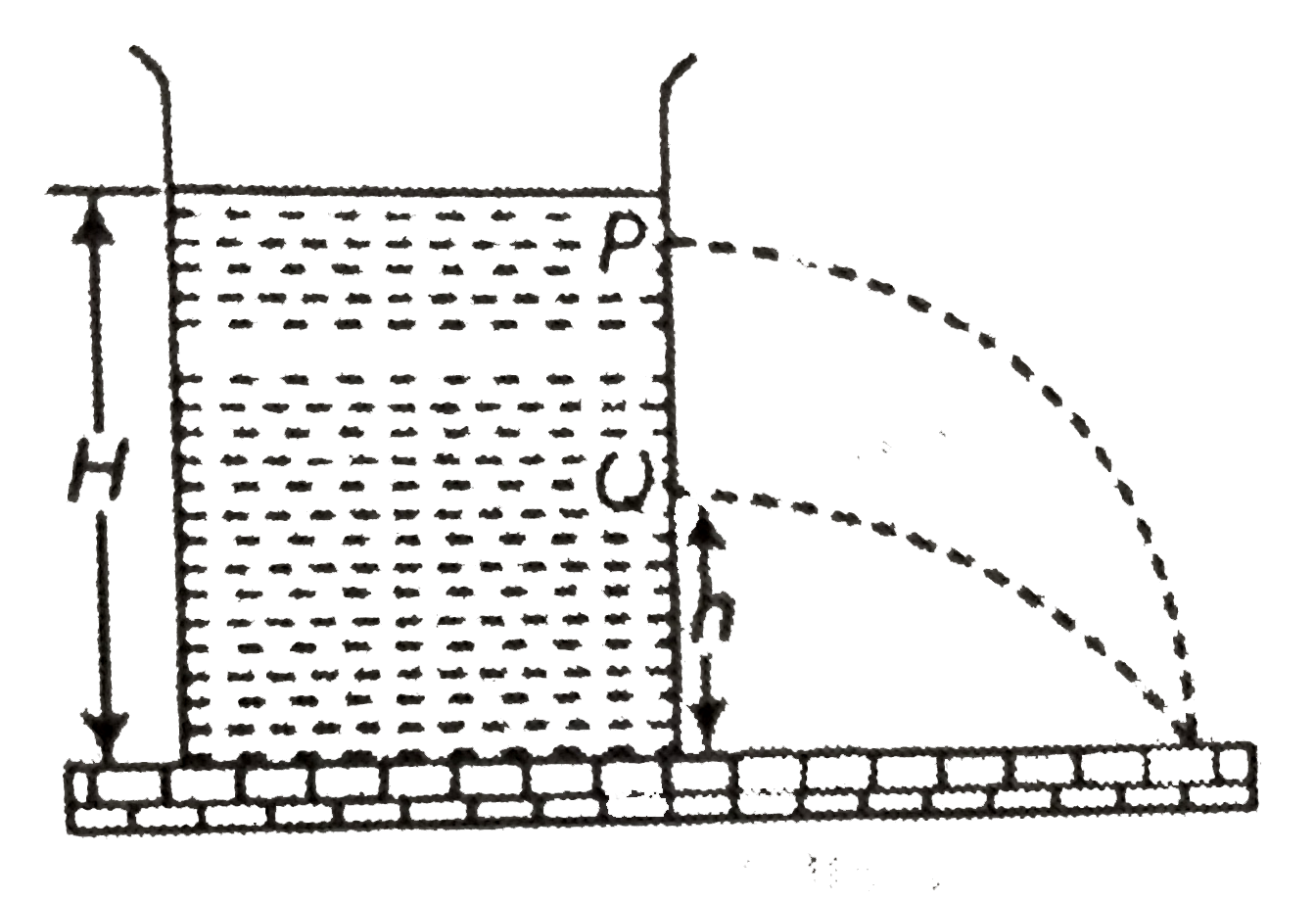
View SolutionA liquid having area of free surface A and has an orifice at a depth of h with an area a, below the liquid surface, then find the velocity v of flow through the orifice
View SolutionA capillary tube of area of cross-section A is dipped in water veritcally. Calculate the amount of heat evolved as the water rises in the capillary tunbe upto height h. The density of water is `rho`
View SolutionThe radius of the biggest metal coin of thickness t and density `rho` which would be able to float on water surface of surface of water is `rho`
View SolutionAn open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. what will be length of the air column above mercury in the above now ?
(Atmospheric pressure = 76 cm of Hg)
View SolutionWhile measuring surface temsoion of water using capillary rise method, heihgt of the lowr meniscus from free surface of water is 3 cm while inner radius of capillary tube is found to be `0.5` cm. Then compute tension of water using this data. (Take contact angle between glass and water and a 0 and `g=9.81 m//s^(2)`
View SolutionTo what depth must a rubber ball be taken in deep sea so that its volume is decreases by `0.1%` (The bulk modulus of rubber is `9.8xx10^(8) N//m` , and the density of sea water is `10^(3) kg//m^(3))`
View SolutionA wooden block or mass m and density `rho` is tied to a string, the other end of the string is fixed to bottom of a tank. The tank is filled with a liquid of density `sigma` with `sigmagtrho`. The tension in the string will be
View SolutionAssume that a drop of liquid evaporates by decreases in its surface energy, so that its temperature remains unchanged. What should be the minimum radius of the drop for this to be possible? The surface tension is T, density of liquid is `rho` and L is its latent heat of vaporization.
View SolutionWater is flowing continuously from a tap having an internal dimeter `8xx10^(-3) m` . The water then, water rises up in it leaves the tap is `0.4 ms^(-1)` . The diameter of the water stream at a distance `2xx10^(-1)`m beblow the tap is close to
View SolutionIn an experiment a capillary tube is kept vertical , then water rises up in the tube upt 3mm height . When the tube is fitted at an angle of `60^(@)` with verical , what should be the height of water rise
View SolutionCalculate for the rise of water in a capillary tube when kept veritcal in water whose radii is 1/4th of that capillry tube which when kept veritcal water rise in it upto a height of 3 mm
View SolutionCalculate the heat evolved for the rise of water when one end of the capillary tube of radius r is immeresed vartically into water. Asssume surface tension =T and density of water to be `rho`
View SolutionIn a liquid threr is air bubble of radius 1 mm at a depth 10 cm below the free space. The surface tension of liquid `0.075n//m` and density is `1000 kg//m^(2)` . By what amout is the pressure indide the bubble greater than the atmospheric preesure ?
View SolutionCalculate the work done by a boy In making a soap bubble of diameter `1.4 cm ` by blowing .if he surface tension of soap solution is `0.03 N//m`
View SolutionA drop of radius r is broken into n equal drips. Calulate the work done if surface tension of water is T.
View SolutionWhat will happen if n drops of a liquid each has surface energy E, combine to form a single drop.
View SolutionIf a bigger drop of liquid at temperature t, breaks up into number of small droplets, then what is temperature of the droplests ? (Assume bigger drop is isolated from its surroundings )
View SolutionThe excess pressure inside a soap bubble of radius 4 cm is `30 "dyne"//cm^(2)` . The surface tension is
View SolutionCalculate the work done against surface tention in fromation of a drop of mercury of radius 4 cm (Surface tension for murcury =465 dyne/cm)
View SolutionCalculate the energy required to increases the radius of a soap bubble from 1 cm to 2 cm (The surface tansion is 30 dyne/cm.)
View SolutionA small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities are`rho` and `sigma(rhogtsigma)` fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
View SolutionA liquid drop of radius R breaks into N smaller droplets of radii r, If liquid has density `rho,` specific heat s and surface tension, T, than the drop in temeperature is given
View Solutionbody of density `rho` is dropped from height h into a liquid having density `sigma(sigmagt rho)` .If the body just touches the of the container, then the distance of fallen would be proprotional to (Neglect viscous forces)
View SolutionA block of mass m and density p is hanging from a string . If it is lowered into a vessel of cross-sectional area A containing a liquid of density `sigma(lt rho)` and gets fully immered, the increase in pressure at the bottom of vessel would be
View SolutionA solid sphere falls with a terminal velocity of 32 m/s in air . If it is allowed to fall in vacuum, then
View SolutionFind the common radius of curvature when two soap bubbles with radii `r_(1)`
View SolutionWater is following in a river. If the velocity of a layer at a distance 10 cm from the bottom is 20n cm/s. Find the velocity of layer at a height of 40 cm from the bottom.
View SolutionA horizontal plate `(10cmxx10cm ) ` moves on a layer of oil of thickness 4 mm with a constant speed of 10 cm/s . The coefficient of viscosity of oil is 4 poise. The constant speed of the plae is
View SolutionA liquid is flowing through a narrow tube. The coefficient of viscosity of liquid is `0.1308` poise. The length and inner radius of tube are 50 cm and 1 min respectively . The rate of flow or liquidn is `360 cm^(3)//min` . Find the pressue difference between ends of tube.
View SolutionFind the terminal velocity of solid shpere or radius `0.1 m` moving in air in vertically downward direction . `(eta=18xx10^(-5) Ns//m^(2)` , density of sphere `=1000 kg//m^(2)` and `g=10^m//s^(2))`
View SolutionEight equal drops of water each of radius r=2 mm are falling through air with a teminaln velocity of 16 cm/s . The eight drops combine to be from a big drop. Calculate the terminal velocit of big drop.
View SolutionAt `20.`C, to attain the terminal velocity how fast willan aluminium sphre of radii 1 mm fall though water. Assume flow to be laminar flow and specific gravity (AI) `=2.7eta_("water")=8xx10^(-4) Pa`
View Solution
Practice Exercise questions and complete solutions for chapter FLUID MECHANICS of BITSAT GUIDE of Class 12