Complete Solutions to Exercises of chapter COORDINATE SYSYEM of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | COORDINATE SYSYEM |
| CENGAGE NEW | Exercises |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
`A B C` is an isosceles triangle. If the coordinates of the base are `B(1,3)` and `C(-2,7)` , the coordinates of vertex `A`
View SolutionIf two vertices of a triangle are (1,3) and (4,-1) and the area of triangle is 5 sq. units, then the angle at the third vertex lies in :
View SolutionWhich of the following sets of points form an equilateral triangle? `(a)(1,0),(4,0),(7,-1)` `(b)(0,0),(3/2,4/3),(4/3,3/2)` `(c)(2/3,),(0,2/3),(1,1)` (d) None of these
View SolutionA particle `p` moves from the point `A(0,4)` to the point `10 ,-4)` . The particle `P` can travel the upper-half plane `{(x , y)|ygeq}` at the speed of `1m//s` and the lower-half plane `{(x , y)|ylt=0}` at the speed of 2 m/s. The coordinates of a point on the x-axis, if the sum of the squares of the travel times of the upper- and lower-half planes is minimum, are (1, 0) (b) (2, 0) (c) (4, 0) (d) (5, 0)
View SolutionIf `|x_1y_1 1x_2y_2 1x_3y_3 1|=|a_1b_1 1a_2b_2 1a_3b_3 1|` then the two triangles with vertices `(x_1, y_1),(x_2,y_2),(x_3,y_3)` and `(a_1,b_1),(a_2,b_2),(a_3,b_3)` are equal to area (b) similar congruent (d) none of these
View Solution`O P Q R` is a square and `M ,N` are the middle points of the sides `P Qa n dQ R` , respectively. Then the ratio of the area of the square to that of triangle `O M N` is 4:1 (b) 2:1 (c) 8:3 (d) 7:3
View SolutionA straight line passing through `P(3,1)` meets the coordinate axes at `Aa n dB` . It is given that the distance of this straight line from the origin `O` is maximum. The area of triangle `O A B` is equal to
View SolutionLet `A-=(3,-4),B-=(1,2)dot` Let `P-=(2k-1,2k+1)` be a variable point such that `P A+P B` is the minimum. Then `k` is 7/9 (b) 0 (c) 7/8 (d) none of these
View SolutionThe polar coordinates equivalent to `(-3,sqrt3)` are
View SolutionIf the point `x_1+t(x_2-x_1),y_1+t(y_2-y_1)` divides the join of `(x_1,y_1)` and `(x_2,y_2)` internally in ratio of `t:1` then vlaue of `t` is
View Solution`P` and `Q` are points on the line joining `A(-2,5)` and `B(3,1)` such that `A P=P Q=Q B` . Then, the distance of the midpoint of `P Q` from the origin is 3 (b) `(sqrt(37))/2` (b) 4 (d) 3.5
View SolutionIn triangle ABC, angle B is right angled, `AC=2` and `A(2,2), B(1,3)` then the length of the median AD is
View SolutionOne vertex of an equilateral triangle is `(2,2)` and its centroid is `(-2/sqrt3,2/sqrt3)` then length of its side is (a) `4sqrt(2)` (b) `4sqrt(3)` (c) `3sqrt(2)` (d) `5sqrt(2)`
View SolutionABCD is a rectangle with `A(-1,2),B(3,7)` and `AB:BC=4:3`. If P is the centre of the rectangle, then the distance of P from each corner is equal to
View SolutionIf `(2,-3), (6,-5)` and `(-2,1)` are three consecutive verticies of a rohmbus, then its area is (a) 24 (b) 36 (c) 18 (d) 48
View SolutionIf poitns `A(3,5)` and B are equidistant from `H(sqrt2,sqrt5)` and B has rational coordinates,then `AB=`
View SolutionLe n be the number of points having rational coordinates equidistant from the point `(0,sqrt3)`, the
View SolutionIn a `triangle ABC` the sides `BC=5, CA=4` and `AB=3`. If `A(0,0)` and the internal bisector of angle A meets BC in D `(12/7,12/7)` then incenter of `triangle ABC` is
View SolutionIf `A(0, 0), B(1, 0) and C(1/2,sqrt(3)/2)` then the centre of the circle for which the lines `AB,BC, CA` are tangents is
View SolutionStatement 1: If in a triangle, orthocentre, circumcentre and centroid are rational points, then its vertices must also be rational points.
Statement : 2 If the vertices of a triangle are rational points, then the centroid, circumcentre and orthocentre are also rational points.
View SolutionConsider three points `P = (-sin (beta-alpha), -cos beta)`, `Q = (cos(beta-alpha), sin beta)`, and `R = ((cos (beta - alpha + theta), sin (beta - theta))`, where `0< alpha, beta, theta < pi/4` Then
View SolutionIf two vertices of a triangle are `(-2,3)` and `(5,-1)` the orthocentre lies at the origin, and the centroid on the line `x+y=7` , then the third vertex lies at
View SolutionThe vertices of a triangle are `(p q ,1/(p q)),(p q)),(q r ,1/(q r)),` and `(r q ,1/(r p)),` where `p ,q` and `r` are the roots of the equation `y^3-3y^2+6y+1=0` . The coordinates of its centroid are `(1,2)` (b) `(2,-1)` (c) `(1,-1)` (d) `(2,3)`
View SolutionIf the vertices of a triangle are `(sqrt(5,)0)` , (`sqrt(3),sqrt(2))` , and `(2,1)` , then the orthocentre of the triangle is (a) `(sqrt(5),0)` (b) `(0,0)` `(sqrt(5)+sqrt(3)+2,sqrt(2)+1)` (d) none of these
View SolutionTwo vertices of a triangle are `(4,-3) & (-2, 5)`. If the orthocentre of the triangle is at `(1,2)`, find coordinates of the third vertex .
View SolutionIn `Delta ABC` if the orthocentre is `(1,2)` and the circumcenter is `(0,0)` then centroid of `Delta ABC` is.
View SolutionA triangle `A B C` with vertices `A(-1,0),B(-2,3/4),` and `C(-3,-7/6)` has its orthocentre at `Hdot` Then, the orthocentre of triangle `B C H` will be `(-3,-2)` (b) `1,3)` `(-1,2)` (d) none of these
View SolutionIf a triangle `A B C ,A-=(1,10),` circumcenter `-=(-1/3,2/3),` and orthocentre `-=((11)/3,4/3)` , then the coordinates of the midpoint of the side opposite to `A` are
View SolutionIn the `DeltaABC`, the coordinates of B are `(0, 0), AB=2, /_ABC=pi/3` and the middle point of BC has the coordinates (2,0). The centroid of the triangle is
View SolutionIf the origin is shifted to the point `((a b)/(a-b),0)` without rotation, then the equation `(a-b)(x^2+y^2)-2a b x=0` becomes
View SolutionA light ray emerging from the point source placed at `P(2,3)` is reflected at a point `Q` on the y-axis. It then passes through the point `R(5,10)dot` The coordinates of `Q` are (a) `(0,3)` (b) `(0,2)` (c) `(0,5)` (d) none of these
View SolutionPoint `P(p ,0),Q(q ,0),R(0, p),S(0,q)` from.
View SolutionA rectangular billiard table has vertices at `P(0,0),Q(0,7),R(10 ,7),` and `S(10 ,0)dot` A small billiard ball starts at `M(3,4)` , moves in a straight line to the top of the table, bounces to the right side of the table, and then comes to rest at `N(7,1)` . The `y-` coordinate of the point where it hits the right side is 3.7 (b) 3.8 (c) 3.9 (d) 4
View SolutionABCD is a square Points `E(4,3)` and `F(2,5)` lie on AB and CD, respectively,such that EF divides the square in two equal parts. If the coordinates of A are `(7,3)`,then the coordinates of other vertices can be
View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
View SolutionA rectangle `A B C D ,` where `A-=(0,0),B-=(4,0),C-=(4,2)D-=(0,2)` , undergoes the following transformations successively: `f_1(x ,y)vec(y ,x)` `f_2(x , y)vec(x+3y ,y)` `f_3(x , y)vec((x-y)//2),(x+y)//2)` The final figure will be square (b) a rhombus a rectangle (d) a parallelogram
View SolutionIf a straight line through the origin bisects the line passing through the given points `(acosalpha,asinalpha)` and `(acosbeta,asinbeta),` then the lines (a) are perpendicular (b) are parallel (c) have an angle between them of `pi/4` (d) none of these
View SolutionLet `A_r ,r=1,2,3, ` , be the points on the number line such that `O A_1,O A_2,O A_3dot` are in `G P ,` where `O` is the origin, and the common ratio of the `G P` be a positive proper fraction. Let `M ,` be the middle point of the line segment `A_r A_(r+1.)` Then the value of `sum_(r=1)^ooO M_r` is equal to
(a) `(O A_1(O S A_1-O A_2))/(2(O A_1+O A_2))` (b) `(O A_1(O A_2+O A_1))/(2(O A_1-O A_2)` (c)`(O A_1)/(2(O A_1-O A_2))` (d) `oo`
View SolutionThe vertices of a parallelogram `A B C D` are `A(3,1),B(13 ,6),C(13 ,21),` and `D(3,16)dot` If a line passing through the origin divides the parallelogram into two congruent parts, then the slope of the line is (a) `(11)/(12)` (b) `(11)/8` (c) `(25)/8` (d) `(13)/8`
View SolutionPoint A and B are in the first quadrant,point O is the origin. If the slope of OA is 1,slope of OB is 7 and OA=OB,Then slope of AB is: a. -1/5 b. -1/4 c. -1/3 d. -1/2
View SolutionLet a,b,c be in A.P and x,y,z be in G.P.. Then the points `(a,x),(b,y)` and `(c,z)` will be collinear if
View SolutionIf `sum_(i-1)^4(x1^2+y 1^2)lt=2x_1x_3+2x_2x_4+2y_2y_3+2y_1y_4,` the points `(x_1, y_1),(x_2,y_2),(x_3, y_3),(x_4,y_4)` are the vertices of a rectangle collinear the vertices of a trapezium none of these
View SolutionThe vertices `A` and `D` of square `A B C D` lie on the positive sides of `x-` and y-axis , respectively. If the vertex `C` is the point `(12 ,17)` , then the coordinates of vertex `B` are (a) `(14 ,16)` (b) (15, 3) (c) `17 ,5)` (d) `(17 ,12)`
View SolutionThrough the point `P(alpha,beta)` , where `alphabeta>0,` the straight line `x/a+y/b=1` is drawn so as to form a triangle of area `S` with the axes. If `a b >0,` then the least value of `S` is (a) `alphabeta` (b) `2alphabeta` (c) `3alphabeta` (d) none
View SolutionThe locus of the moving point whose coordinates are given by `(e^t+e^(-t),e^t-e^(-t))` where `t` is a parameter, is (a) `x y=1` (b) `x+y=2` (c) `x^2-y^2=4` (d) `x^2-y^2=2`
View SolutionThe locus of a point represent by
`x=(a)/(2)((t+1)/(t)),y=(a)/(2)((t-1)/(t))`, where `t=in R-{0}`, is
View SolutionVertices of a variable triangle are `(3,4); (5costheta, 5sintheta)` and `(5sintheta,-5costheta)` where `theta` is a parameter then the locus of its orthocentre is a. `(x+y-1)^2+(x-y-7)^2=100` b. `(x+y-7)^2+(x-y-1)^2=100` c. `(x+y-7)^2+(x+y-1)^2=100` d. `(x+y-7)^2+(x-y+1)^2=100`
View SolutionVertices of a variable triangle are `(3,4); (5costheta, 5sintheta)` and `(5sintheta,-5costheta)` where `theta` is a parameter then the locus of its orthocentre is a. `(x+y-1)^2+(x-y-7)^2=100` b. `(x+y-7)^2+(x-y-1)^2=100` c. `(x+y-7)^2+(x+y-1)^2=100` d. `(x+y-7)^2+(x-y+1)^2=100`
View SolutionFrom a point, P perpendicular PM and PN are drawn to x and y axes, respectively. If MN passes through fixed point (a,b), then locus of P is
View SolutionThe locus of point of intersection of the lines `y+mx=sqrt(a^2m^2+b^2)` and `my-x=sqrt(a^2+b^2m^2)` is
View SolutionIf the roots of the equation
`(x_(1)^(2)-a^2)m^2-2x_1y_1m+y_(1)^(2)+b^2=0(agtb)` are the slopes of two perpendicular lies intersecting at `P(x_1,y_1)`, then the locus of P is
View SolutionThrough point `P(-1,4)`, two perpendicular lines are drawn which intersect x-axis at Q and R. find the locus of incentre of `Delta PQR`. a. `x^2+y^2+2x-8y-17=0` b. `x^2-y^2 +2x-8y+17=0` c. `x^2+y^2-2x-8y-17=0` d. `x^2-y^2+8x-2y-17=0`
View SolutionThe number of integral points (x,y) (i.e, x and y both are integers) which lie in the first quadrant but not on the coordinate axes and also on the straight line `3x + 5y = 2007` is equal to
View SolutionThe foot of the perpendicular on the line `3x+y=lambda` drawn from the origin is `Cdot` If the line cuts the `x` and the y-axis at `Aa n dB` , respectively, then `B C: C A` is
View SolutionThe image of `P(a,b)` on the line `y=-x` is Q and the image of Q on the line `y=x` is 'R' find the mid-point of 'P' and 'R'
View SolutionIf the equation of the locus of a point equidistant from the points `(a_1,b_1)` and `(a_2,b_2)` is `(a_1-a_2)x+(b_2+b_2)y+c=0`, then the value of C is
View SolutionConsider three lines as follows. `L_1:5x-y+4=0` `L_2:3x-y+5=0` `L_3: x+y+8=0` If these lines enclose a triangle `A B C` and the sum of the squares of the tangent to the interior angles can be expressed in the form `p/q ,` where `pa n dq` are relatively prime numbers, then the value of `p+q` is
View SolutionConsider a point A(m,n) , where m and n are positve intergers. B is the reflection of A in the line `y=x`, C is the reflaction of B in the y axis, D is the reflection of C in the x axis and E is the reflection of D is the y axis. The area of the pentagon ABCDE is a. `2m (m+n)` b. `m (m+3n)` c. `m(2m+3n)` d. `2m(m+3n)`
View SolutionIn the given figure, OABC is a rectangle. Slope of OB is
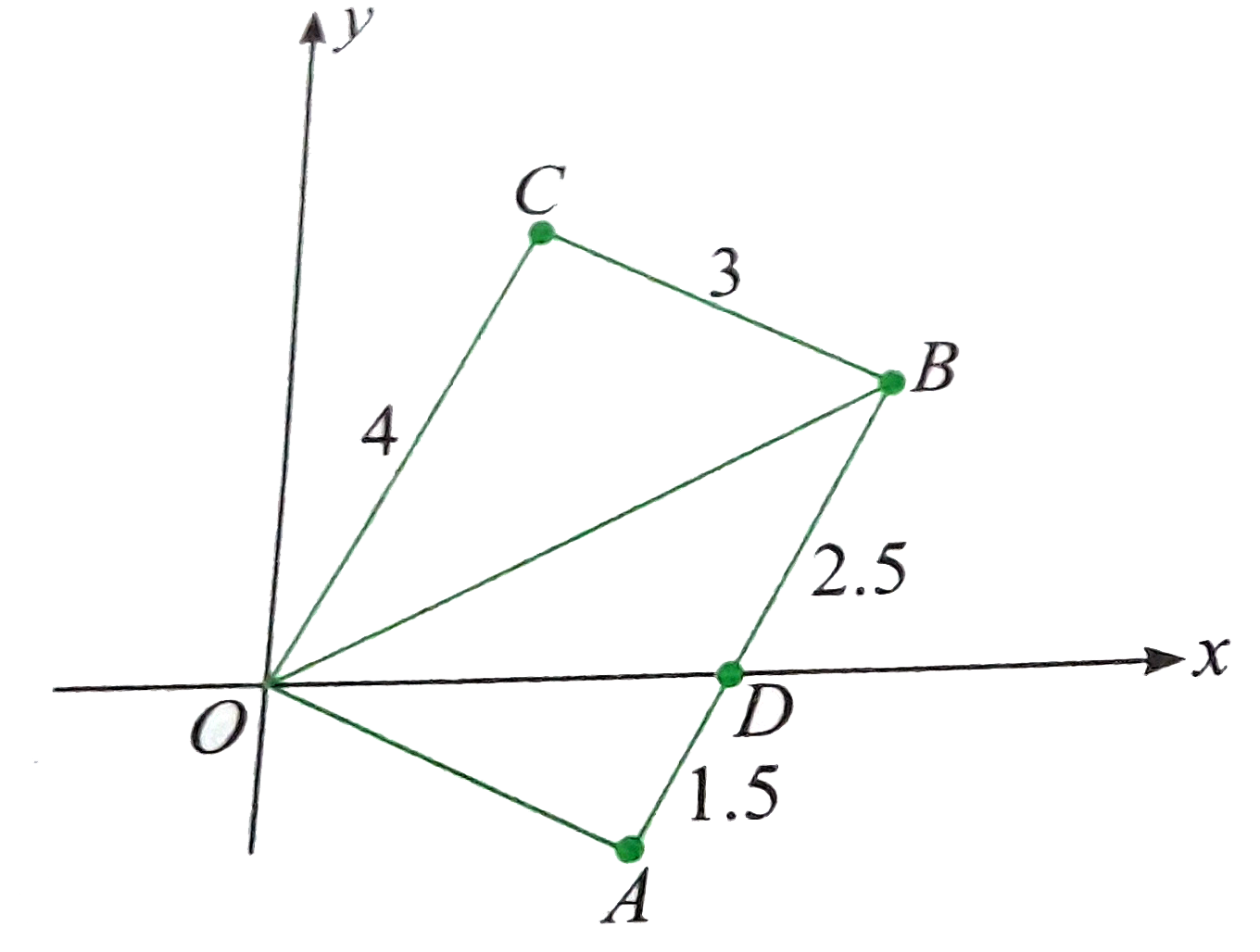 a. `1//4`
b. `1//3`
c. `1//2`
d. Cannot be determined
a. `1//4`
b. `1//3`
c. `1//2`
d. Cannot be determined
View Solution
Exercises questions and complete solutions for chapter COORDINATE SYSYEM of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS COORDINATE SYSYEM
- Concept applications 1.1
- Concept applications 1.2
- Concept applications 1.3
- Concept applications 1.4
- Concept applications 1.5
- Concept applications 1.6
- Exercises
- Illustration1.1
- Illustration1.10
- Illustration1.11
- Illustration1.12
- Illustration1.13
- Illustration1.14
- Illustration1.15
- Illustration1.16
- Illustration1.17
- Illustration1.18
- Illustration1.19
- Illustration1.2
- Illustration1.20
- Illustration1.21
- Illustration1.22
- Illustration1.23
- Illustration1.24
- Illustration1.25
- Illustration1.26
- Illustration1.27
- Illustration1.28
- Illustration1.29
- Illustration1.3
- Illustration1.30
- Illustration1.31
- Illustration1.32
- Illustration1.33
- Illustration1.34
- Illustration1.35
- Illustration1.36
- Illustration1.37
- Illustration1.38
- Illustration1.39
- Illustration1.4
- Illustration1.40
- Illustration1.41
- Illustration1.42
- Illustration1.43
- Illustration1.44
- Illustration1.45
- Illustration1.46
- Illustration1.47
- Illustration1.48
- Illustration1.49
- Illustration1.5
- Illustration1.50
- Illustration1.51
- Illustration1.52
- Illustration1.53
- Illustration1.54
- Illustration1.55
- Illustration1.56
- Illustration1.57
- Illustration1.58
- Illustration1.59
- Illustration1.6
- Illustration1.60
- Illustration1.61
- Illustration1.62
- Illustration1.63
- Illustration1.64
- Illustration1.65
- Illustration1.66
- Illustration1.67
- Illustration1.7
- Illustration1.8
- Illustration1.9
- JEE Main
- Linked
- Matrix match type
- Multiple correct
- Numerical value
- Solved examples