Complete Solutions to Linkded Comprehension Type of chapter AREA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | AREA |
| CENGAGE NEW | Linkded Comprehension Type |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
Let `A_(r)` be the area of the region bounded between the curves `y^(2)=(e^(-kr))x("where "k gt0,r in N)" and the line "y=mx ("where "m ne 0)`, k and m are some constants
`A_(1),A_(2),A_(3),…` are in G.P. with common ratio
View SolutionLet `A_(r)` be the area of the region bounded between the curves `y^(2)=(e^(-kr))x("where "k gt0,r in N)" and the line "y=mx ("where "m ne 0)`, k and m are some constants
`lim_(n to oo)Sigma_(i=1)^(n)A_(i)=(1)/(48(e^(2k)-1))` then the value of m is
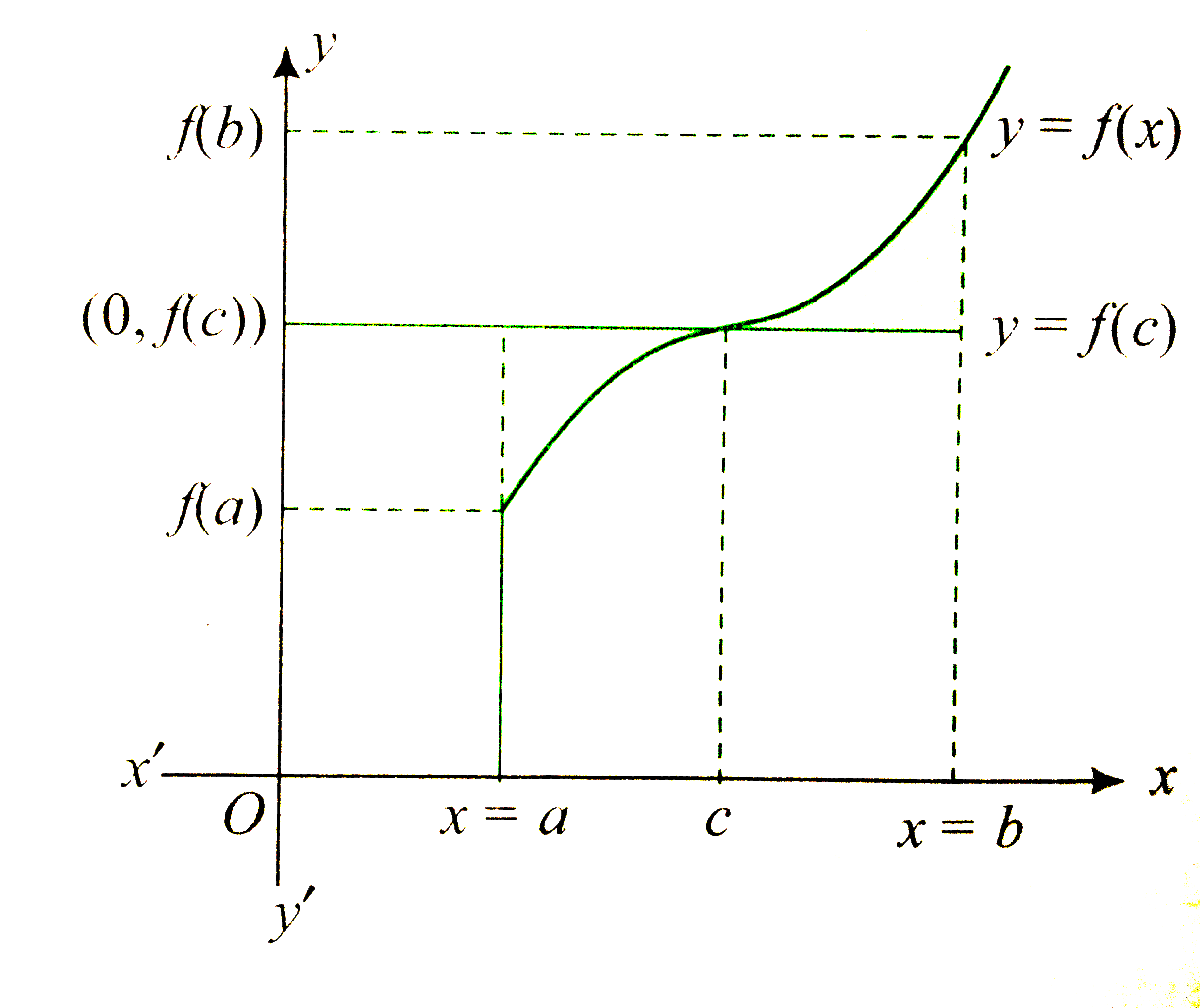
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at `x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2)`.
`"Proof : " A=int_(a)^(c)(f(c)-f(x))dx+int_(c)^(b)(f(c))dx`
`=f(c)(c-a)-int_(a)^(c)(f(x))dx+int_(a)^(b)(f(x))dx-f(c)(b-c)`
`rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b)(f(x))dx-int_(a)^(c)(f(x))dx`
Differentiating w.r.t. c, we get
`(dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0)`
For maxima and minima , `(dA)/(dc)=0`
`rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0)`
Hence, `c=(a+b)/(2)`
`"Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0`
Hence, A is minimum when `c=(a+b)/(2)`.
If the area bounded by `f(x)=(x^(3))/(3)-x^(2)+a` and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
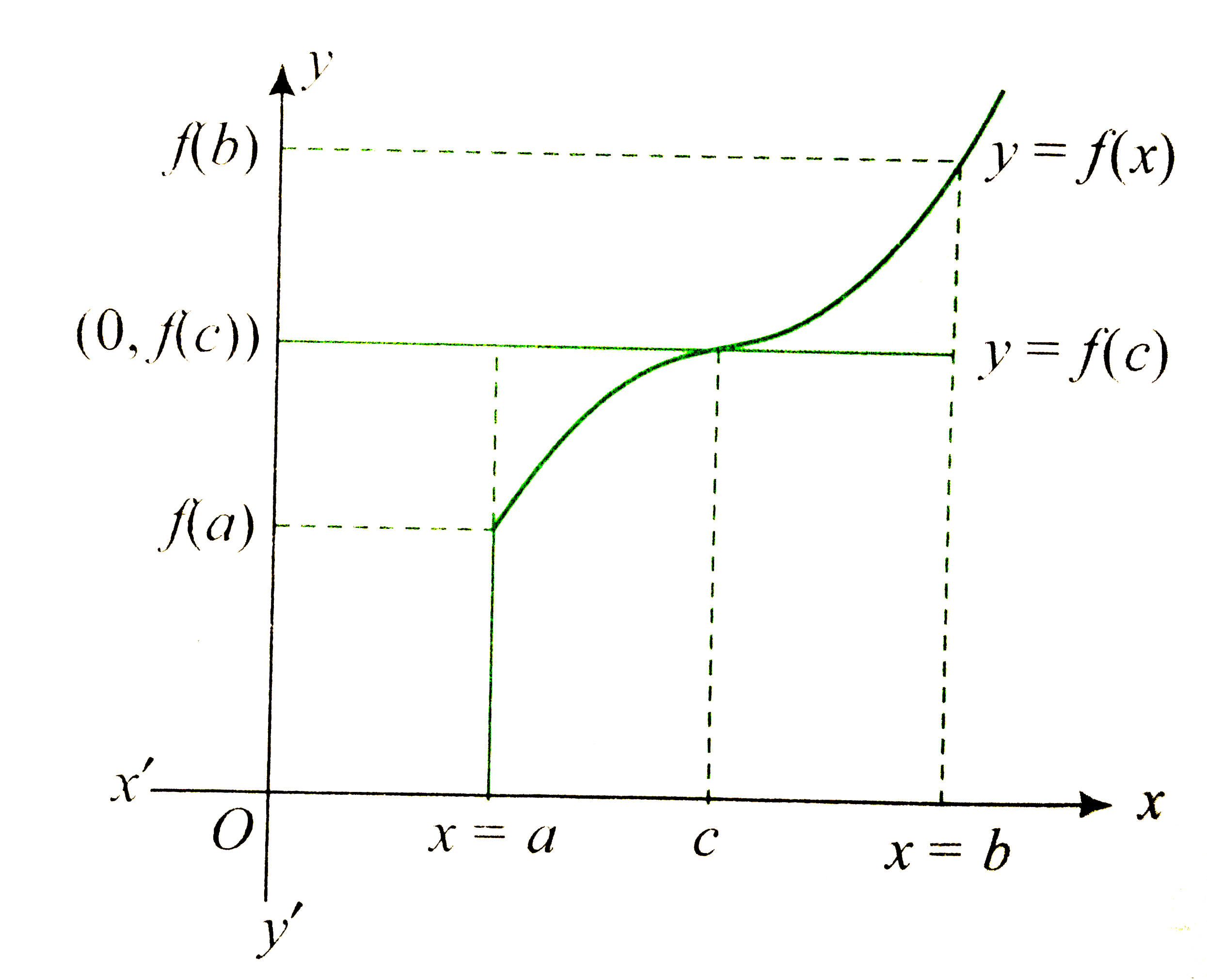
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at `x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when`
` "c=(a+b)/(2)`.
`"Proof : " A=int_(a)^(c) (f(c)-f(x))dx+int_(c)^(b) (f(c))dx`
`=f(c)(c-a)-int_(a)^(c) (f(x))dx+int_(a)^(b) (f(x))dx-f(c)(b-c)`
`rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b) (f(x))dx-int_(a)^(c) (f(x))dx`
Differentiating w.r.t. c, we get
`(dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0)`
For maxima and minima , `(dA)/(dc)=0`
`rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0)`
Hence, `c=(a+b)/(2)`
`"Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0`
Hence, A is minimum when `c=(a+b)/(2)`.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function `y=x^(3)+3x^(2)+x+a`, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is
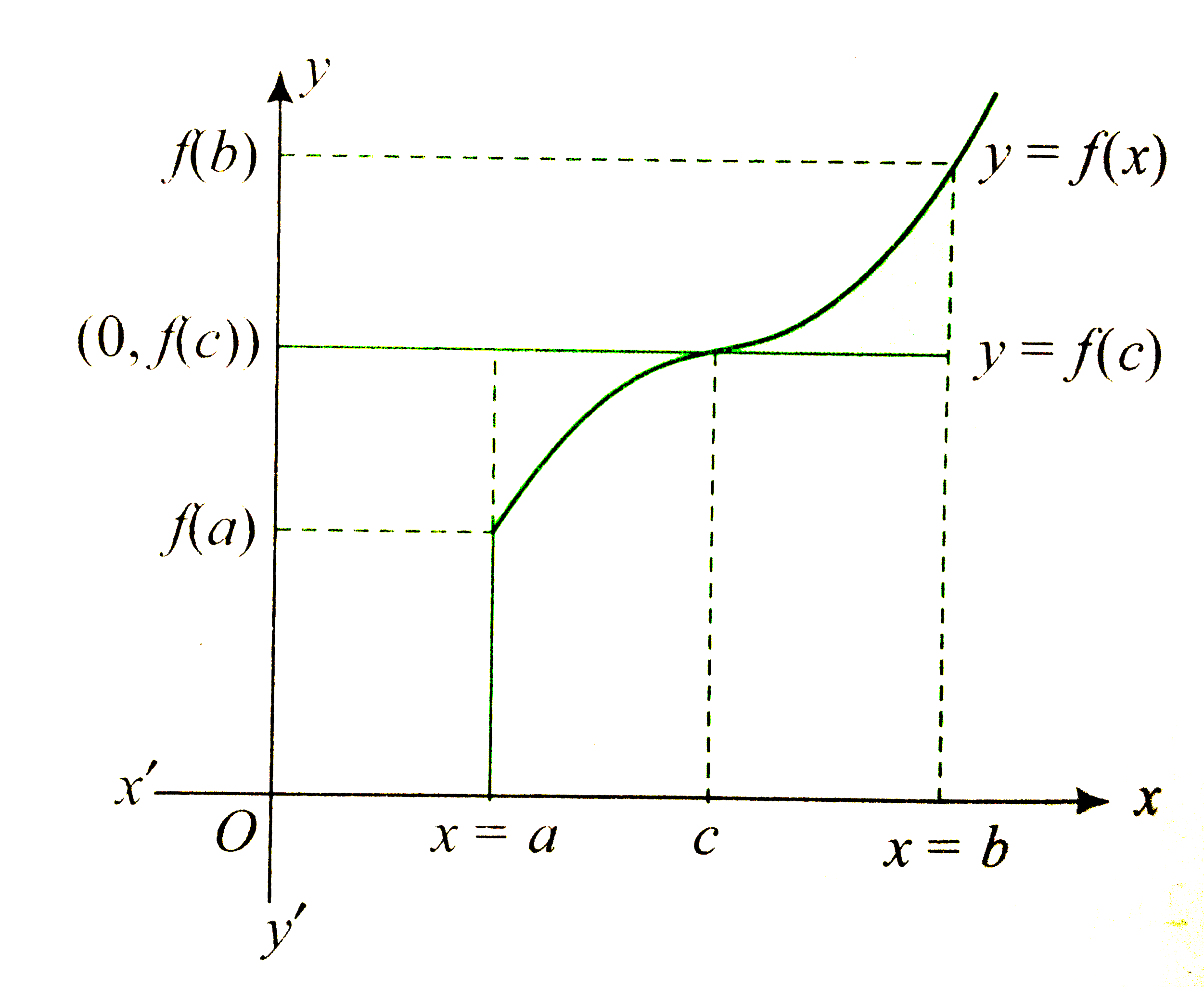
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at `x=a, x=b, y=f(x) and y=f(c)("where "c in (a,b))" is minimum when "c=(a+b)/(2)`.
`"Proof : " A=int_(a)^(c)(f(c)-f(x))dx+int_(c)^(b)(f(c))dx`
`=f(c)(c-a)-int_(a)^(c) (f(x))dx+int_(a)^(b)(f(x))dx-f(c)(b-c)`
`rArr" "A=[2c-(a+b)]f(c)+int_(c)^(b)(f(x))dx-int_(a)^(c)(f(x))dx`
Differentiating w.r.t. c, we get
`(dA)/(dc)=[2c-(a+b)]f'(c)+2f(c)+0-f(c)-(f(c)-0)`
For maxima and minima , `(dA)/(dc)=0`
`rArr" "f'(c)[2c-(a+b)]=0(as f'(c)ne 0)`
Hence, `c=(a+b)/(2)`
`"Also for "clt(a+b)/(2),(dA)/(dc)lt0" and for "cgt(a+b)/(2),(dA)/(dc)gt0`
Hence, A is minimum when `c=(a+b)/(2)`.
If the area enclosed by `f(x)= sin x + cos x, y=a` between two consecutive points of extremum is minimum, then the value of a is
View SolutionConsider the area `S_(0),S_(1),S_(2)….` bounded by the x-axis and half-waves of the curve `y=e^(-x) sin x," where "x ge 0.`
The value of `S_(0)` is
View SolutionConsider the sequence of natural numbers `s_0,s_1,s_2`,... such that `s_0 =3, s_1 = 3 and s_n = 3 + s_(n-1) s_(n-2)`, then
View SolutionConsider the area `S_(0),S_(1),S_(2)….` bounded by the x-axis and half-waves of the curve `y=e^(-x) sin x," where "x ge 0.`
The value of `S_(0)` is
View SolutionTwo curves `C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12,` satisfying the relation `"(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))`
The area bounded by the curve `C_(1) and C_(2)` is
View SolutionTwo curves `C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12,` satisfying the relation `"(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))`
The area bounded by the curve `C_(2) and |x|+|y|=sqrt(12)` is
View SolutionTwo curves `C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12,` satisfying the relation `"(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))`
The area bounded by `C_(1) and x+y+2=0` is
View SolutionConsider the two curves `C_(1):y=1+cos x and C_(2): y=1 + cos (x-alpha)" for "alpha in (0,(pi)/(2))," where "x in [0,pi].` Also the area of the figure bounded by the curves `C_(1),C_(2), and x=0` is same as that of the figure bounded by `C_(2),y=1, and x=pi`.
The value of `alpha` is
View SolutionConsider two curves `C_1: y=1/x a n dC_2: y=1nx` on the `x y` plane. Let `D_1` denotes the region surrounded by `C_1,C_2,` and the line `x=1a n dD_2` denotes the region surrounded by `C_1,C_2` and the line `x=adot` If `D_1=D_2,` then the sum of logarithm of possible value of `a` is _____________
View SolutionConsider the function defined implicity by the equation `y^(2)-2ye^(sin^(-1)x)+x^(2)-1+[x]+e^(2sin ^(-1)x)=0("where [x] denotes the greatest integer function").`
The area of the region bounded by the curve and the line `x=-1` is
View SolutionConsider the function defined implicity by the equation `y^(2)-2ye^(sin^(-1)x)+x^(2)-1+[x]+e^(2sin ^(-1)x)=0("where [x] denotes the greatest integer function").`
Line x=0 divides the region mentioned above in two parts. The ratio of area of left-hand side of line to that of right-hand side of line is
View SolutionConsider two functions
`f(x)={([x]",",-2le x le -1),(|x|+1",",-1 lt x le 2):} and g(x)={([x]",",-pi le x lt 0),(sinx",",0le x le pi):}`
where [.] denotes the greatest integer function.
The exhaustive domain of `g(f(x))` is
View SolutionComputing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., `x=x(t), y=(t),` then the area of the figure is evaluated by one of the three formulas :
`S=-int_(alpha)^(beta)y(t)x'(t)dt,`
`S=int_(alpha)^(beta)x(t)y'(t)dt,`
`S=(1)/(2)int_(alpha)^(beta)(xy'-yx')dt,`
Where `alpha and beta` are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
The area of the region bounded by an are of the cycloid `x=a(t-sin t), y=a(1- cos t)` and the x-axis is
View SolutionComputing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., `x=x(t), y=(t),` then the area of the figure is evaluated by one of the three formulas :
`S=-int_(alpha)^(beta)y(t)x'(t)dt,`
`S=int_(alpha)^(beta)x(t)y'(t)dt,`
`S=(1)/(2)int_(alpha)^(beta)(xy'-yx')dt,`
Where `alpha and beta` are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
The area of the loop described as
`x=(t)/(3)(6-t),y=(t^(2))/(8)(6-t)` is
View SolutionComputing area with parametrically represented boundaries : If the boundary of a figure is represented by parametric equation, i.e., `x=x(t), y=(t),` then the area of the figure is evaluated by one of the three formulas :
`S=-int_(alpha)^(beta) y(t)x'(t)dt,`
`S=int_(alpha)^(beta) x(t)y'(t)dt,`
`S=(1)/(2)int_(alpha)^(beta)(xy'-yx')dt,`
Where `alpha and beta` are the values of the parameter t corresponding respectively to the beginning and the end of the traversal of the curve corresponding to increasing t.
If the curve given by parametric equation `x=t-t^(3), y=1-t^(4)` forms a loop for all values of `t in [-1,1]` then the area of the loop is
View SolutionLet f(x) be a continuous function fiven by `f(x)={(2x",", |x|le1),(x^(2)+ax+b",",|x|gt1):},"then "`
If f(x) is continuous for all real x then the value of `a^(2)+b^(2)` is
View SolutionLet `f(x)` be continuous function given by `f(x)={2x ,|x|lt=1`and `x^2+a x+b ,|x|>1}dot`
Find the area of the region in the third quadrant bounded by the curves `x=-2y^2a n dy=f(x)` lying on the left of the line `8x+1=0.`
View Solution
Linkded Comprehension Type questions and complete solutions for chapter AREA of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS AREA
- Archives
- Comprehension Type
- Concept Application Exercise 9.1
- Concept Application Exercise 9.2
- Concept Application Exercise 9.3
- Exercises - Single Correct Answer Type
- ILLUSTRATION
- Linkded Comprehension Type
- Matrix Match Type
- Multiple Correct Answer Type
- Multiple Correct Answers Type
- Numerical Value Type
- Single Correct Answer Type
- Solved Examples