Complete Solutions to ILLUSTRATION of chapter AREA of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | AREA |
| CENGAGE NEW | ILLUSTRATION |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
Find the area of the closed figure bounded by the curves `y=sqrt(x),y=sqrt(4-3x)a n dy=0`
View SolutionFind the area, lying above the x=axis and included between the circle `x^2+y^2=8x` and the parabola `y^2=4xdot`
View SolutionFind the area bounded by
(i) y`=log""_(e)|x|andy=0`
(ii) `y=|log""_(e)|x||andy=0`
View SolutionFind the area bounded by `y=1/(x^2-2x+2)` and x-axis.
View Solutionfind the area of y = 3 − 2 x − x^2
View SolutionIf the area of bounded between the x-axis and the graph of `y=6x-3x^2` between the ordinates `x=1a n dx=a` is `19` units, then `a` can take the value `4or-2` two value are in (2,3) and one in `(-1,0)` two value are in (3,4) and one in `(-2,-1)` none of these
View SolutionProve that area common to ellipse `(x^2)/(a^2)+(y^2)/(b^2)=1` and its auxiliary circle `x^2+y^2=a^2` is equal to the area of another ellipse of semi-axis a and a-b.
View SolutionLet `f(x)=` maximum `{x^2, (1-x)^2, 2x(1 - x)}` where `x in [0, 1].` Determine the area of the region bounded by the curve `y=f(x)` and the lines `y = 0,x=0, x=1.`
View SolutionConsider the region formed by the lines `x=0,y=0,x=2,y=2.` If the area enclosed by the curves `y=e^x a n dy=1nx ,` within this region, is being removed, then find the area of the remaining region.
View SolutionDraw a rough sketch of the curve `y=(x^2+3x+2)/(x^2-3x+2)` and find the area of the bounded region between the curve and the x-axis.
View SolutionFind the area bounded by the curve `y=(x-1)(x-2)(x-3)` lying between the ordinates `x=0a n dx=3.`
View SolutionFind the area bounded by the curve `x={{:(-2-y",",ylt-1),(y^(3)",",-1leyle1),(2-y",",ygt1):}` and x=0 is
View SolutionFind the area enclosed by the graph of `y=log_(e)(x+1),`y-axis, and the line y=1
View SolutionFind the area bounded by the curve `y=sin^(-1)x` and the line `x=0,|y|=pi/2dot`
View SolutionFind the area of the region bounded by the curves `y=sqrt(x+2) and y=(1)/(x+1)` between the lines x=0 and x=2.
View SolutionFind the area bounded by `y=sin^(-1)x ,y=cos^(-1)x` ,and the `X`-axis.
View SolutionFind the area bounded by the parabola `y=x^2+1` and the straight line `x+y=3.`
View SolutionFind the area bounded by the curves `y=sin xa n dy=cosx` between two consecutive points of the intersection.
View SolutionFind the ratio in which the area bounded by the curves `y^2=12 x and x^2=12 y` is divided by the line `x=3.`
View SolutionFind the area of the figure bounded by the parabolas `x=-2y^2, x=1-3y^2dot`
View SolutionThe area common to regions `x^2+y^2-2xlt=0` and `ygeq sin (pix/2)
View SolutionFind the area of the region enclosed by the curves `y=xlogx` and `y=2x-2x^2dot`
View SolutionFind the area bounded by `y^2lt=4x ,x^2+y^2geq2x ,a n dxlt=y+2` in the first quadrant.
View SolutionSketch the region bounded by the curves `y=x^2a n dy=2/(1+x^2)` . Find the area.
View SolutionFind the area bounded by the curves `y=x^(3)-x and y=x^(2)+x.`
View SolutionFind the area bounded by `y=-x^(3)+x^(2)+16x and y=4x`
View SolutionFind the area of the region enclosed by `y=-5x-x^(2) and y=x` on interval `[-1,5]`
View SolutionIf the area enclosed by curve `y=f(x)a n dy=x^2+2` between the abscissa `x=2a n dx=alpha,alpha>2,` is `(alpha^3-4alpha^2+8)s qdot` unit. It is known that curve `y=f(x)` lies below the parabola `y=x^2+2.`
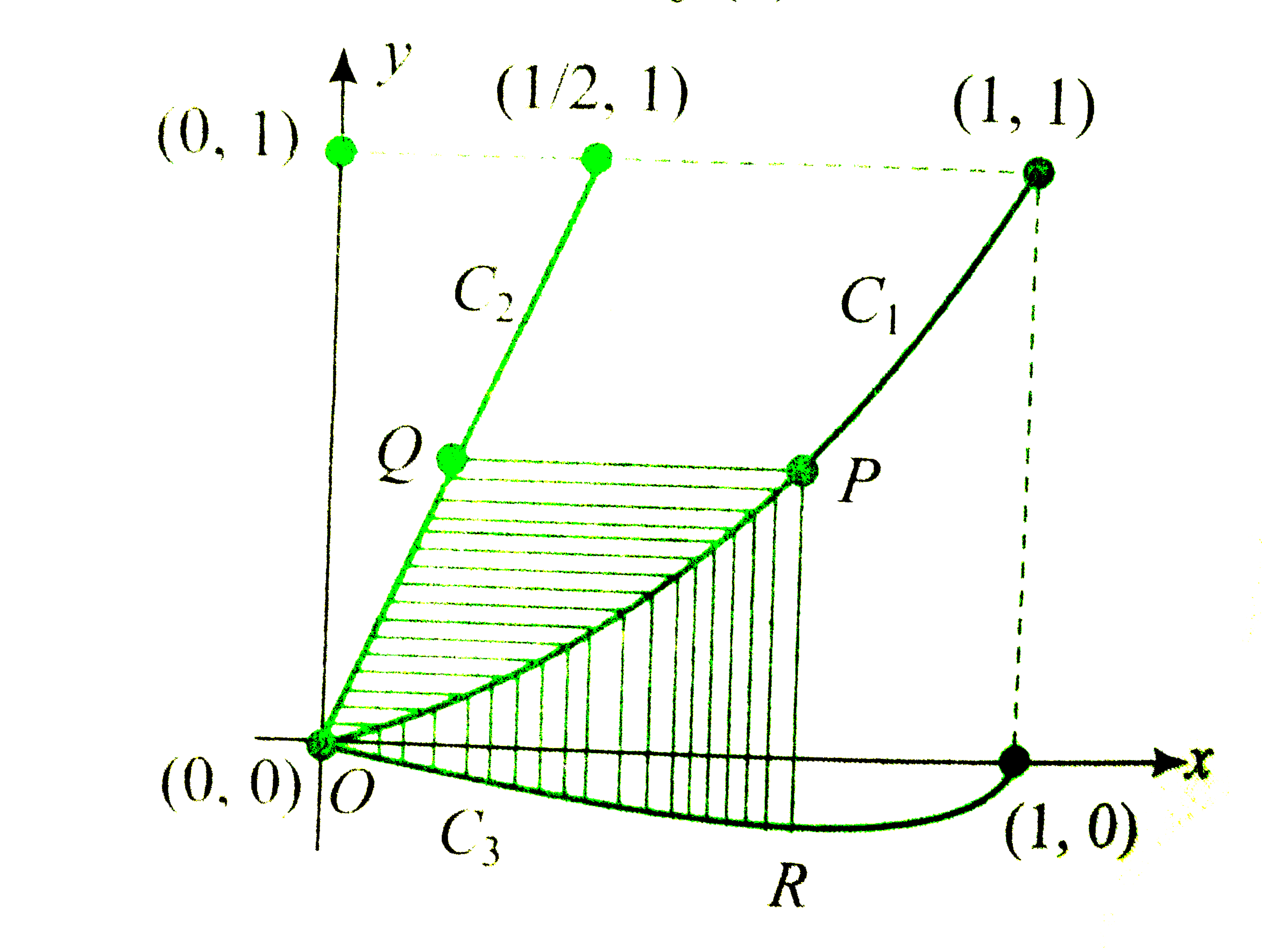
View SolutionLet `C_(1) and C_(2)` be the graphs of the functions `y=x^(2) and y=2x,` respectively, where `0le x le 1." Let "C_(3)` be the graph of a function y=f(x), where `0lexle1, f(0)=0.` For a point P on `C_(1),` let the lines through P, parallel to the axes, meet `C_(2) and C_(3)` at Q and R, respectively (see figure). If for every position of `P(on C_(1)),` the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionIf the area bounded by `f(x)=sqrt(tan x), y=f(c), x=0 and x=a, 0ltcltalt(pi)/(2)` is minimum then find the value of c.
View SolutionFind the area of the region `R` which is enclosed by the curve `ygeqsqrt(1-x^2)` and max `{|x|,|y|}lt=4.`
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line `x=3.`
View SolutionConsider a square with vertices at `(1, 1), (-1, 1), (-1, -1) and (1, -1)`. Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionLet `O(0,0),A(2,0),a n dB(1 1/(sqrt(3)))` be the vertices of a triangle. Let `R` be the region consisting of all those points `P` inside ` O A B` which satisfy `d(P , O A)lt=min[d(p ,O B),d(P ,A B)]` , where `d` denotes the distance from the point to the corresponding line. Sketch the region `R` and find its area.
View SolutionFind the area enclosed by `y=g(x),` x-axis, x=1 and x=37, where g(x) is inverse of `f(x)=x^(3)+3x+1`.
View SolutionFind the area bounded by the curve `f(x)=x+ sin x and ` its inverse function between the ordinates `x=0" to "x=2pi`.
View Solution
ILLUSTRATION questions and complete solutions for chapter AREA of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS AREA
- Archives
- Comprehension Type
- Concept Application Exercise 9.1
- Concept Application Exercise 9.2
- Concept Application Exercise 9.3
- Exercises - Single Correct Answer Type
- ILLUSTRATION
- Linkded Comprehension Type
- Matrix Match Type
- Multiple Correct Answer Type
- Multiple Correct Answers Type
- Numerical Value Type
- Single Correct Answer Type
- Solved Examples