Complete Solutions to Single correct Answer of chapter THEORY OF EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THEORY OF EQUATIONS |
| CENGAGE NEW DPP | Single correct Answer |
| Number Of Questions | 69 |
| Academic Year | 2023-24 |
Number of real solutions of `sqrt(2x-4)-sqrt(x+5)=1` is
03:28View SolutionNumber of real solutions of `sqrt(x)+sqrt(x-sqrt(1-x))=1` is
04:57View SolutionThe set of real values of `a` for which the equation `(2a^(2)+x^(2))/(a^(3)-x^(3))-(2x)/(ax+a^(2)+x^(2))+(1)/(x-1)=0` has a unique solution is
04:56View SolutionNumber of distinct real solutions of the equation `x^(2)+((x)/(x-1))^(2)=8` is
03:27View SolutionIf `m`, `n` are positive integers and `m+nsqrt(2)=sqrt(41+24sqrt(2))`, then `(m+n)` is equal to
01:48View SolutionThe equation `(x+3-4(x-1)^(1//2))^(1//2)+(x+8-6(x-1)^(1//2))^(1//2)=1` has (A) no solution (B) only `1` solution (C) only `2` solutions (D) more than `2` solutions
05:31View SolutionThe number of solutions of `sqrt(3x^(2)+x+5)=x-3` is (A) `0` (B) `1` (C) `2` (D) `4`
02:38View SolutionThe number of real or complex solutions of `x^(2)-6|x|+8=0` is
07:18View SolutionIf `alpha, beta` are the roots of the quadratic equation `x^2 - 3x - 2(3^(log_3 2) - 2^(log_2 3))) = 0` then the value of `alpha^2 + alpha beta + beta^2` is equal to
06:20View SolutionWhich of the following is not true for equation `x^(2)log8-xlog5=2(log2)-x` (A) equation has one integral root (B) equation has no irrational roots (C) equation has rational roots (D) none of these
03:32View SolutionLet `f(x)` be a quadratic expression such that `f(-1)+f(2)=0`. If one root of `f(x)=0` is `3`, then the other root of `f(x)=0` lies in (A) `(-oo,-3)` (B) `(-3,oo)` (C) `(0,5)` (D) `(5,oo)`
03:28View SolutionIf `f(x)=(x^(2)+3x+2)(x^(2)-7x+a)` and `g(x)=(x^(2)-x-12)(x^(2)+5x+b)`, then the value of `a` and `b`, if `(x+1)(x-4)` is H.C.F. of `f(x)` and `g(x)` is
03:18View SolutionThe remainder obtained when the polynomial `x+x^(3)+x^(9)+x^(27)+x^(81)+x^(243)` is divided by `x^(2)-1` is
02:39View SolutionLet `f(x)=x^(2)-ax+b`, `'a'` is odd positive integar and the roots of the equation `f(x)=0` are two distinct prime numbers. If `a+b=35`, then the value of `f(10)=`
02:42View SolutionIf `0 lt alpha lt beta lt gamma lt pi//2`, then the equation
`(x-sinbeta)(x-singamma)+(x-sinalpha)(x-singamma)+(x-sinalpha)(x-sinbeta)=0` hasView SolutionIf the system of equation `r^(2)+s^(2)=t` and `r+s+t=(k-3)/(2)` has exactly one real solution, then the value of `k` is
04:03View SolutionIf `a,` b`. `c in R` and `3b^(2)-8ac lt 0`, then the equation `ax^(4)+bx^(3)+cx^(2)+5x-7=0` has
View SolutionFor real solution of equation `3sqrt(x+3p+1)-3sqrt(x)=1`, we have
03:14View SolutionFor `a`, `b`,`c` non-zero, real distinct, the equation, `(a^(2)+b^(2))x^(2)-2b(a+c)x+b^(2)+c^(2)=0` has non-zero real roots. One of these roots is also the root of the equation :
06:29View SolutionThe equation `x^(2)+bx+c=0` has distinct roots. If `2` is subtracted from each root the result are the reciprocal of the original roots, then `b^(2)+c^(2)` is
03:35View SolutionThe equation `(x^(2)+3x+4)^(2)+3(x^(2)+3x+4)+4=x` has
01:17View SolutionIf one root of the equation `(x-1)(7-x)=m` is three times the other, then `m` is equal to
02:10View SolutionIf the roots of the equation `ax^(2)-4x+a^(2)=0` are imaginery and the sum of the roots is equal to their product then `a` is
02:49View SolutionIf the sum of squares of roots of equation `x^(2)-(sin alpha-2)x-(1+sin alpha)=0` is the least, then `alpha` is equal to
03:50View SolutionIf `alpha` and `beta` are the roots of the equation `ax^(2)+bc+c=0` then the sum of the roots of the equation `a^(2)x^(2)+(b^(2)-2ac)x+b^(2)-4ac=0` is
02:46View SolutionIf the roots of the quadratic equation `ax^(2)+bx-b=0`, where `a`, `b in R` such that `a*b gt 0`, are `alpha` and `beta`, then the value of `log_(|(beta-1)|)|(alpha-1)|` is
06:04View SolutionIf `cos^4 alpha +k and sin^4 alpha+k` are the roots of `x^2+lambda(2 x+1)=0 and sin^2 alpha+1 and cos^2 alpha +1` are the roots of `x^2 +8 x+4=0,` then the sum of the possible values of `lambda` is
03:57View SolutionLet `f(x)=ax^(2)+bx+c`, `g(x)=ax^(2)+qx+r`, where `a`, `b`, `c`,`q`, `r in R` and `a lt 0`. If `alpha`, `beta` are the roots of `f(x)=0` and `alpha+delta`, `beta+delta` are the roots of `g(x)=0`, then
07:48View SolutionIf `a`, `b`, `c` are in geometric progresion and the roots of the equations `ax^(2)+2bx+c=0` are `alpha` and `beta` and those of `cx^(2)+2bx+a=0` are `gamma` and `delta` then
03:52View SolutionIf `alpha`, `beta` are the roots of the equation `ax^(2)+bx+c=0` and `S_(n)=alpha^(n)+beta^(n)`, then `aS_(n+1)+bS_(n)+cS_(n-1)=(n ge 2)`
03:18View SolutionLet `f(x)=ax^(2)+bx+c`, `g(x)=ax^(2)+px+q`, where `a`, `b`, `c`, `q`, `p in R` and `b ne p`. If their discriminants are equal and `f(x)=g(x)` has a root `alpha`, then
05:52View SolutionIf `alpha` and `beta` be the roots of equation `x^(2) + 3x + 1 = 0`, then the value of `((alpha)/(1 + beta))^(2) + ((beta)/(1 + alpha))^(2)` is equal to
03:52View SolutionThe roots of the equation `a(b-2x)x^(2)+b(c-2a)x+c(a-2b)=0` are, when `ab+bc+ca=0`
03:46View SolutionIf the equations `2x^(2)-7x+1=0` and `ax^(2)+bx+2=0` have a common root, then
03:34View SolutionIf `alpha` and `beta`, `alpha` and `gamma`, `alpha` and `delta` are the roots of the equations `ax^(2)+2bx+c=0`, `2bx^(2)+cx+a=0` and `cx^(2)+ax+2b=0` respectively where `a`, `b`, `c` are positive real numbers, then `alpha+alpha^(2)` is equal to
03:20View SolutionThe product of uncommon real roots of the polynomials ` p(x)=x^4+2x^3-8x^2-6x+15` and ` q(x) ` `= x^3+4x^2-x-10 ` is :
06:23View SolutionNumber of values of `x` satisfying the pair of quadratic equations `x^(2)-px+20=0` and `x^(2)-20x+p=0` for some `p in R` is
03:53View SolutionIf the equations `4x^(2)-x-1=0` and `3x^(2)+(lambda+mu)x+lambda-mu=0` have a root common, then the rational values of `lambda` and `mu` are
04:32View SolutionIf the equations `x^(2)+2lambdax+lambda^(2)+1=0`, `lambda in R` and `ax^(2)+bx+c=0` , where `a`, `b`, `c` are lengths of sides of triangle have a common root, then the possible range of values of `lambda` is
07:30View SolutionIf both the roots of `k(6x^(2)+3)+rx+2x^(2)-1=0` and `6k(2x^(2)+1)+px+4x^(2)-2=0` are common, then `2r-p` is equal to
04:52View Solution`x^(3)+5x^(2)+px+q=0` and `x^(3)+7x^(2)+px+r=0` have two roos in common. If their third roots are `gamma_(1)` and `gamma_(2)` , respectively, then `|gamma_(1)-gamma_(2)|=`
06:36View SolutionLet `a,b in N, a != b` and the two quadratic equations `(a-1)x^2-(a^2+2)x+a^2+2a=0 and (b-1)x^2-(b^2+2)x+(b^2+2b)=0` have a common root. The value of `ab` is
04:30View SolutionA quadratic equations `p(x)=0` having coefficient `x^(2)` unity is such that `p(x)=0` and `p(p(p(x)))=0` have a common root, then
04:31View SolutionIf `ax^2+bx+c=0 and cx^2 + bx+a=0(a,b,c in R)` have a common non-real roots, then which of the following is not true ?
04:44View SolutionLet `A={x|x^2 + (m - 1)x -2(m +1)=0, x in R}, {B = {x|(m-1)x^2 + mx + 1 = 0, x in R}` Number of values of m such that `AuuB` has exactly 3 distinct elements, is
09:31View SolutionIf the equation `|x^2-5x + 6|-lambda x+7 lambda=0` has exactly 3 distinct solutions then `lambda` is equal to
07:21View SolutionLet `alpha`, `beta (a lt b)` be the roots of the equation `ax^(2)+bx+c=0`. If `lim_(xtom) (|ax^(2)+bx+c|)/(ax^(2)+bx+c)=1` then
02:26View SolutionIf the quadratic polynomials defined on real coefficient
`P(x)=a_(1)x^(2)+2b_(1)x+c_(1)` and `Q(x)=a_(2)x^(2)+2b_(2)x+c_(2)` take positive values `AA x in R`, what can we say for the trinomial `g(x)=a_(1)a_(2)x^(2)+b_(1)b_(2)x+c_(1)c_(2)` ?02:29View SolutionFor which of the following graphs the quadratic expression `y=ax^(2)+bx+c` the product `abc` is negative ?
View SolutionThe difference of maximum and minimum value of `(x^(2)+4x+9)/(x^(2)+9)` is
04:20View SolutionIf `a gt 1` , then the roots of the equation `(1-a)x^(2)+3ax-1=0` are
04:43View SolutionThe values of `'a'` for which the quadraic expression `ax^(2)+(a-2)x-2` is negative for exactly two integral values of `x`, belongs to
05:01View SolutionIf the roots of equation `(a + 1)x^2-3ax + 4a = 0` (a is not equals to -1) are greater than unity, then
14:27View SolutionThe equation `ax^(4)-2x^(2)-(a-1)=0` will have real and unequal roots if
04:19View SolutionIf `ax^(2)+bx+c=0`, `a ne 0`, `a`, `b`, `c in R` has distinct real roots in `(1,2)`, then `a` and `5a+2b+c` have
04:56View SolutionIf `c lt a lt b lt d`, then roots of the equation `bx^(2)+(1-b(c+d)x+bcd-a=0`
04:06View SolutionIf `2a`, `b`, `2c` are in `A.P.` where `a`, `b`, `c` are `R^(+)`, then the expression `f(x)=(ax^(2)-bx+c)` has
03:17View SolutionIf `a`, `b`, `c` are positive numbers such that `a gt b gt c` and the equation `(a+b-2c)x^(2)+(b+c-2a)x+(c+a-2b)=0` has a root in the interval `(-1,0)`, then
04:13View SolutionIf the quadratic equation `x^(2)-36x+lambda=0` has roots `alpha` and `beta` such that `alpha`, `beta in N` and `(lambda)/(5) cancel in Z` and `lambda` assumes minimum possible value then `(sqrt(alpha+2)sqrt(beta+2))/(|alpha-beta|)` is equal to
01:45View SolutionIf the equation `2^(2x)+a*2^(x+1)+a+1=0` has roots of opposite sign, then the exhaustive set of real values of `a` is
View SolutionLet `a`, `b`, `c` ne three distinct non-zero real numbers satisfying the system of equation `(1)/(a)+(1)/(a-1)+(1)/(a-2)=1` , `(b)+(1)/(b-1)+(1)/(b-2)=1` , `(1)/(c )+(1)/(c-1)+(1)/(c-2)=1`. Then `abc=`
03:53View SolutionIn the given figure graph of `y=p(x)=x^(4)+ax^(3)+bx^(2)+cx+d` is given
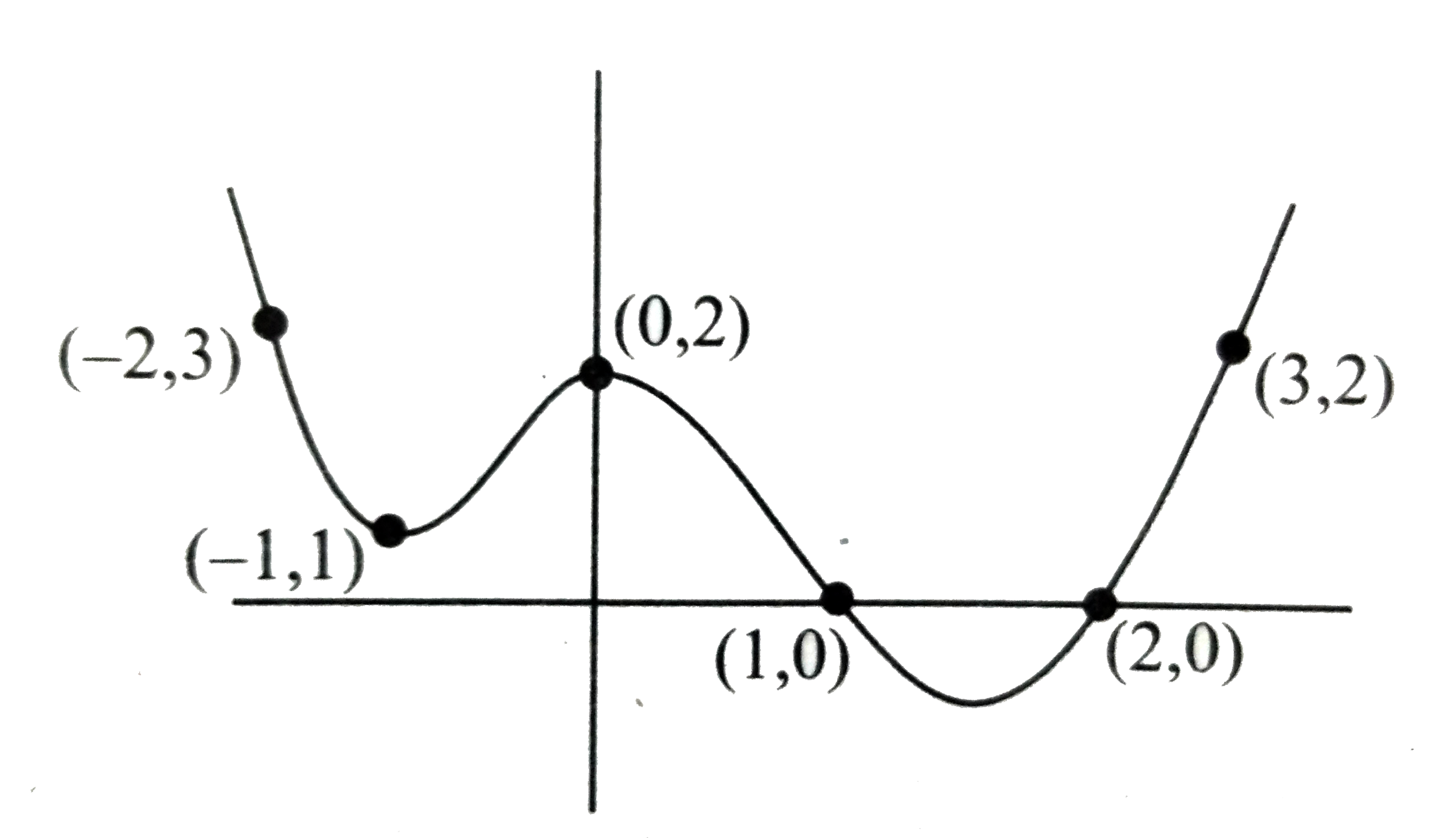
The product of all imaginery roots of `p(x)=(0)` is03:38View SolutionIf `a^(3)-3a^(2)+5a-17=0` and `b^(3)-3b^(2)+5b+11=0` are such that `a+b` is a real number, then the value of `a+b` is
06:20View SolutionLet` f(x) = x^4 + ax^3 + bx^2 + cx + d` be a polynomial with real coefficients and real roots. If |f(i)|=1where `i=sqrt(-1)`, then the value of a +b+c+d is
04:43View SolutionIf f(x) is a polynomial of degree four with leading coefficient one satisfying `f(1)=1, f(2)=2,f(3)=3`.then `[(f(-1)+f(5))/(f(0)+f(4))]`
10:43View SolutionLet `p(x) =x^6-x^5-x^3-x^2-x` and `alpha, beta, gamma, delta` are the roots of the equation `x^4-x^3-x^2-1=0` then `P(alpha)+P(beta)+P(gamma)+P(delta)=`
05:39View SolutionThe line `y=mx+1` touches the curves `y=0x^(4)+2x^(2)+x` at two points `P(x_(1),y_(1))` and `Q(x_(2),y_(2))`. The value of `x_(1)^(2)+x_(2)^(2)+y_(1)^(2)+y_(2)^(2)` is
View SolutionIf `a+b+c=24`, `a^(2)+b^(2)+c^(2)=210`, `abc=440`. Then the least value of `a-b-c` is
04:37View SolutionIf the roots of `x^(4)+qx^(2)+kx+225=0` are in arthmetic progression, then the value of `q`, is
07:01View Solution
Single correct Answer questions and complete solutions for chapter THEORY OF EQUATIONS of CENGAGE MATHS (HINGLISH) of Class 12
All Exercises from CENGAGE NEW DPP Class 12 MATHS THEORY OF EQUATIONS
- Comprehension
- Examples
- Exercise (Comprehension)
- Exercise (Matrix)
- Exercise (Multiple)
- Exercise (Numerical)
- Exercise (Single)
- Exercise 2.1
- Exercise 2.10
- Exercise 2.11
- Exercise 2.12
- Exercise 2.13
- Exercise 2.2
- Exercise 2.3
- Exercise 2.4
- Exercise 2.5
- Exercise 2.6
- Exercise 2.7
- Exercise 2.8
- Exercise 2.9
- JEE Advanced Previous Year
- JEE Main Previous Year
- Multiple Correct Answer
- Single correct Answer
