Complete Solutions to Exercise (Comprehension) of chapter CIRCLE of Class 12 book with complete answers and questions

Each side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to `x+y= 0`. Find the co-ordinates of the vertices of the square.

Each side of a square has length 4 units and its center is at (3,4). If one of the diagonals is parallel to the line `y=x`, then anser the following questions.
The radius of the circle inscribed in the triangle formed by any three vertices is

Each side of a square has length 4 units and its center is at (3,4). If one of the diagonals is parallel to the line `y=x`, then anser the following questions. ,brgt The radius of the circle inscribed in the triangle formed by any two vertices of the square and the center is

Tangents PA and PB are drawn to the circle `(x-4)^(2)+(y-5)^(2)=4` from the point P on the curve`y=sin x` , where A and B lie on the circle. Consider the function `y= f(x)` represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The range of `y=f(x)` is

Tangents PA and PB are drawn to the circle `(x-4)^(2)+(y-5)^(2)=4` from the point P on the curve`y=sin x` , where A and B lie on the circle. Consider the function `y= f(x)` represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The period of `y=f(x)` is

Tangents PA and PB are drawn to the circle `(x-4)^(2)+(y-5)^(2)=4` from the point P on the curve`y=sin x` , where A and B lie on the circle. Consider the function `y= f(x)` represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?

Consider a family of circles passing through the points (3, 7) and (6,5). Answer the following questions. Number of circles which belong to the family and also touchingx- axis are

Consider a family of circles passing through the point (3,7) and (6,5). Answer the following questions.
If each circle in the family cuts the circle `x^(2)+y^(2)-4x-6y-3=0`, then all the common chords pass through the fixed point which is

Consider a family of circles passing through the point (3,7) and (6,5). Answer the following questions.
If the circle which belongs to the given family cuts the circle `x^(2)+y^(20=29` orthogonally, then the center of that circle is

If `4l^2-5m^2+6l+1=0.` Prove that `lx+my+1=0` touches a definite circle. Find the centre & radius of the circle.

Consider the relation `4l^(2)-5m^(2)+6l+1=0` , where `l,m in R`
Tangents PA and PB are drawn to the above fixed circle from the points P on the line `x+y-1=0` . Then the chord of contact AP passes through the fixed point.

Consider the relation `4l^(2)-5m^(2)+6l+1=0` , where `l,m in R`. The number of tangents which can be drawn from the point `(2,-3)` to the above fixed circle are

A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that `DeltaOAP` is a right angled triangle at A and its perimeter is 8 units. The length of `QP` is

A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that `DeltaOAP` is a right angled triangle at A and its perimeter is 8 units. The length of `QP` is

A circle C whose radius is 1 unit, touches the x-axis at point A. The centre Q of C lies in first quadrant. The tangent from origin O to the circie touches it at T and a point P lies on it such that `DeltaOAP` is a right angled triangle at A and its perimeter is 8 units. The length of `QP` is

P is a variable point of the line L = 0. Tangents are drawn to the circle `x^2 + y^2 = 4` from P to touch it at Q and R. The parallelogram PQSR is completed. If `L = 2x + y - 6 = 0`, then the locus of circumcetre of `trianglePQR` is -

P is a variable point on the line `L=0` . Tangents are drawn to the circles `x^(2)+y^(2)=4` from P to touch it at Q and R. The parallelogram PQSR is completed.
If `P-= (6,8)`, then the area of `Delta QRS` is

P is a variable point on the line `L=0` . Tangents are drawn to the circles `x^(2)+y^(2)=4` from P to touch it at Q and R. The parallelogram PQSR is completed.
If `P -=(3,4)`, then the coordinates of S are

To the circle `x^2 + y^2 = 4` two tangents are drawn from `P (-4, 0)`, which touch the circle at `T_1`, and `T_2` and a rhombus `PT_1P'T_2` is completed. Circumcentre of the triangle `PT_1T_2` is at

To the circle `x^2 + y^2 = 4` two tangents are drawn from `P (-4, 0)`, which touch the circle at `T_1`, and `T_2` and a rhombus `PT_1P'T_2` is completed. Circumcentre of the triangle `PT_1T_2` is at

To the circle `x^(2)+y^(2)=4`, two tangents are drawn from `P(-4,0)`, which touch the circle at `T_(1)` and `T_(2)` . A rhomus `PT_(1)P'T_(2)` s completed.
If P is taken to be at (h,0) such that P' lies on the circle, the area of the rhombus is

Let `alpha` chord of a circle be that chord of the circle which subtends an angle `alpha` at the center.
If `x+y=1` is a chord of `x^(2)+y^(2)=1`, then `alpha` is equal to

Let `alpha` chord of a circle be that chord of the circle which subtends an angle `alpha` at the center.
If the slope of a `pi//3` chord of `x^(2)+y^(2)=4 ` is 1, then its equation is

Let `alpha` chord of a circle be that chord of the circle which subtends an angle `alpha` at the center.
The distance of `2pi //3` chord of `x^(2)+y^(2)+2x+4y+1=0` from the center is

Two variable chords AB and BC of a circle `x^(2)+y^(2)=a^(2)` are such that `AB=BC=a`. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
`/_ OAB` is

Two variable chords AB and BC of a circle `x^(2)+y^(2)=a^(2)` are such that `AB=BC=a`. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The angle between the tangents at A and C is

Two variable chords AB and BC of a circle `x^(2)+y^(2)=a^(2)` are such that `AB=BC=a`. M and N are the midpoints of AB and BC, respectively, such that the line joining MN intersects the circles at P and Q, where P is closer to AB and O is the center of the circle.
The locus of the points of intersection of tangents at A and C is

Give two circles intersecting orthogonally having the length of common chord `24//5` units. The radius of one of the circles is 3 units.
The radius of other circle is

Give two circles intersecting orthogonally having the length of common chord `24//5` units. The radius of one of the circles is 3 units.
The angle between direct common tangents is

Give two circles intersecting orthogonally having the length of common chord `24//5` units. The radius of one of the circles is 3 units.
The length of direct common tangent is

In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio `5:3` What is the ratio of the length of AB to that of BR ?

In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio `5:3`

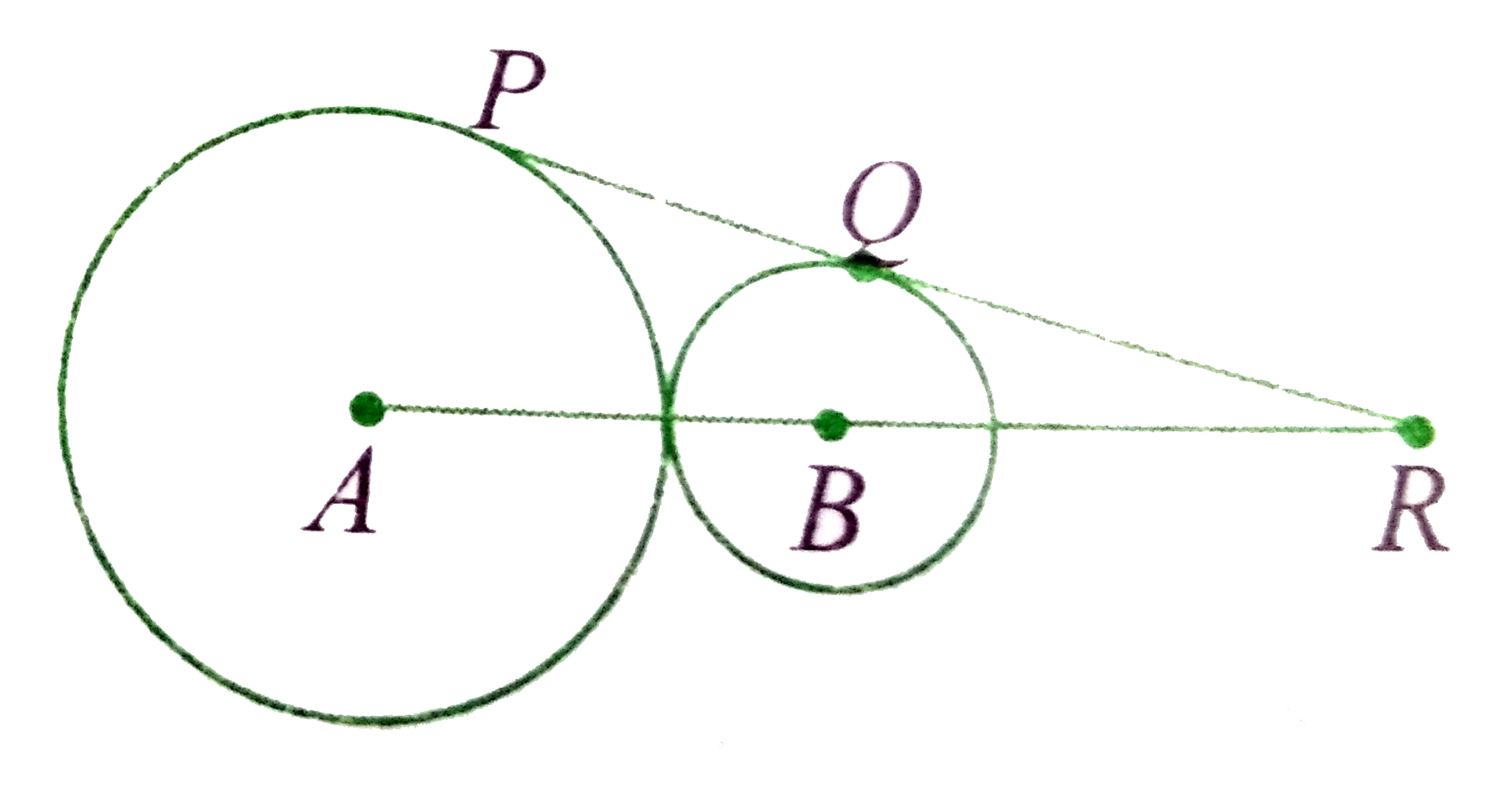
The radius of the circle with center B is

In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio `5:3`

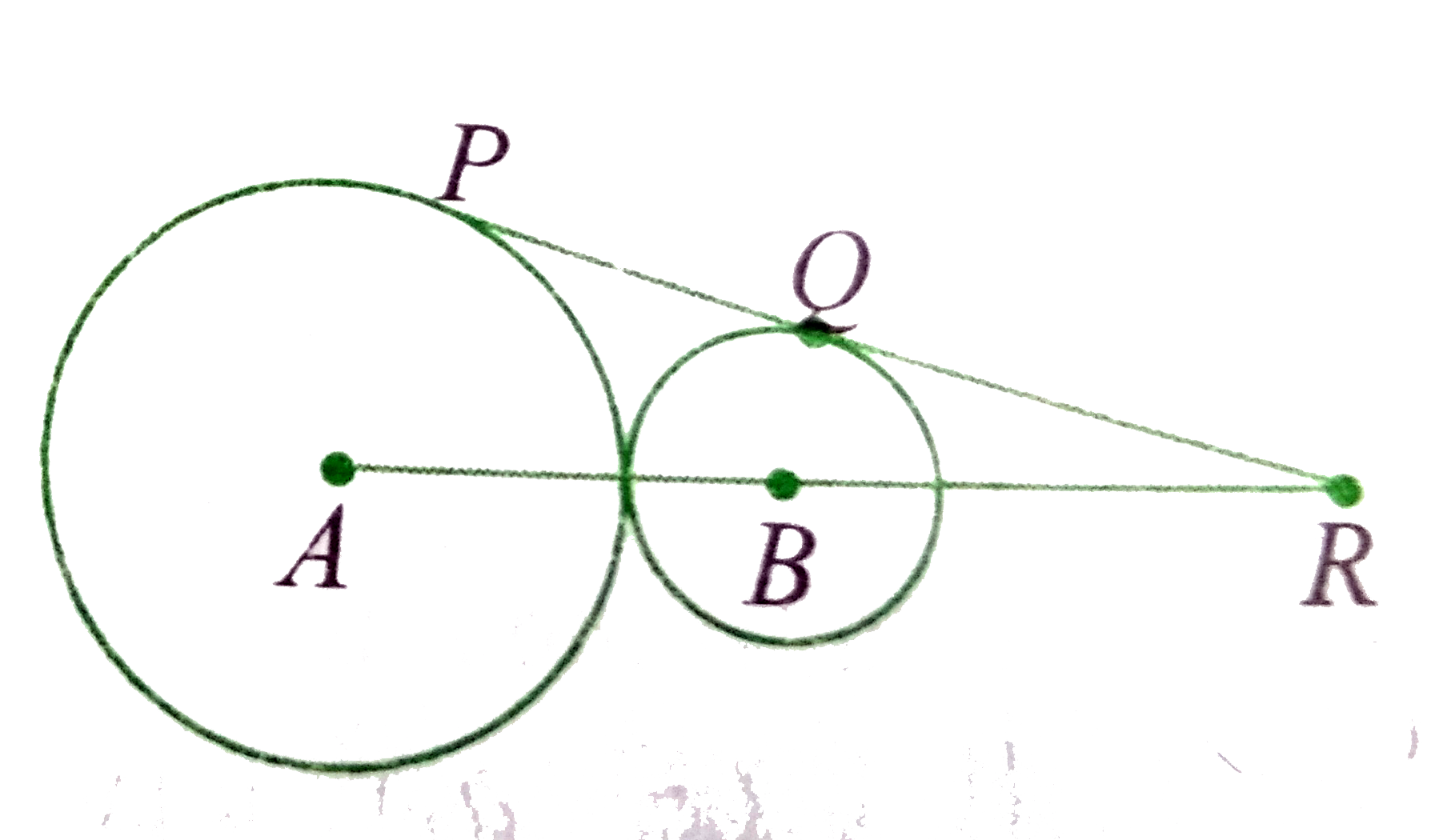
The length of QR is

Let each of the circles
`S_(1)-=x^(2)+y^(2)+4y-1=0`
`S_(1)-= x^(2)+y^(2)+6x+y+8=0`
`S_(3)-=x^(2)+y^(2)-4x-4y-37=0`
touch the other two. Also, let `P_(1),P_(2)` and `P_(3)` be the points of contact of `S_(1)` and `S_(2) , S_(2)` and `S_(3)`, and `S_(3)` , respectively, `C_(1),C_(2)` and `C_(3)` are the centres of `S_(1),S_(2)` and `S_(3)` respectively.
The coordinates of `P_(1)` are

Let each of the circles
`S_(1)-=x^(2)+y^(2)+4y-1=0`
`S_(1)-= x^(2)+y^(2)+6x+y+8=0`
`S_(3)-=x^(2)+y^(2)-4x-4y-37=0`
touch the other two. Also, let `P_(1),P_(2)` and `P_(3)` be the points of contact of `S_(1)` and `S_(2) , S_(2)` and `S_(3)`, and `S_(3)` , respectively, `C_(1),C_(2)` and `C_(3)` are the centres of `S_(1),S_(2)` and `S_(3)` respectively.
The ratio `("area"(DeltaP_(1)P_(2)P_(3)))/("area"(DeltaC_(1)C_(2)C_(3)))` is equal to

Let each of the circles
`S_(1)-=x^(2)+y^(2)+4y-1=0`
`S_(1)-= x^(2)+y^(2)+6x+y+8=0`
`S_(3)-=x^(2)+y^(2)-4x-4y-37=0`
touch the other two. Also, let `P_(1),P_(2)` and `P_(3)` be the points of contact of `S_(1)` and `S_(2) , S_(2)` and `S_(3)`, and `S_(3)` , respectively, `C_(1),C_(2)` and `C_(3)` are the centres of `S_(1),S_(2)` and `S_(3)` respectively.
`P_(2)` and `P_(3)` are images of each other with respect to the line

The line `x + 2y = a` intersects the circle `x^2 + y^2 = 4` at two distinct points `A and B` Another line `12x - 6y - 41 = 0` intersects the circle `x^2 + y^2 - 4x - 2y + 1 = 0` at two `C and D`. The value of `a` for which the points `A,B,C and D` are concyclic -

The line `x + 2y = a` intersects the circle `x^2 + y^2 = 4` at two distinct points `A and B` Another line `12x - 6y - 41 = 0` intersects the circle `x^2 + y^2 - 4x - 2y + 1 = 0` at two `C and D`. The value of 'a' for which the points `A,B,C and D` are concyclic -

Let A,B, and C be three sets such that
`A={(x,y)|(x)/(cos theta)=(y)/(sintheta)=5,"where" 'theta'"is parameter"}`
`B= {(x,y)|(x-3)/(cos phi)=(y-4)/(sin phi)=r}`
`C= { (x,y)|(x-3)^(2)+(y-4)^(2)leR^(2)}`
If `A capC =A`, then minimum value of R is

Let A,B, and C be three sets such that
`A={(x,y)|(x)/(cos theta)=(y)/(sintheta)=5,"where" 'theta'"is parameter"}`
`B= {(x,y)|(x-3)/(cos phi)=(y-4)/(sin phi)=r}`
`C= { (x,y)|(x-3)^(2)+(y-4)^(2)leR^(2)}`
If `phi` is fixed and r varies and `(A cap B) =1`, then `sec phi` is equal to

Consider the family of circles `x^(2)+y^(2)-2x-2ay-8=0` passing through two fixed points A and B . Also, `S=0` is a cricle of this family, the tangent to which at A and B intersect on the line `x+2y+5=0`.
The distance between the points A and B , is

Show that equation `x^2+y^2-2ay-8=0` represents, for different values of 'a, asystem of circles"passing through two fixed points A, B on the X-axis, and find the equation ofthat circle of the system the tangents to which at AB meet on the line `x+ 2y + 5 = 0`.

Consider the family of circles `x^(2)+y^(2)-2x-2ay-8=0` passing through two fixed points A and B . Also, `S=0` is a cricle of this family, the tangent to which at A and B intersect on the line `x+2y+5=0`.
If the circle `x^(2)+y^(2)-10x+2y=c=0` is orthogonal to `S=0`, then the value of c is

A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation `sqrt3 x+ y -6 = 0` and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are

A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation `sqrt3 x+ y -6 = 0` and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are

A circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ, QR, RP are D, E, F, respectively. The line PQ is given by the equation `sqrt3 x+ y -6 = 0` and the point D is (3 sqrt3/2, 3/2). Further, it is given that the origin and the centre of C are on the same side of the line PQ. (1)The equation of circle C is (2)Points E and F are given by (3)Equation of the sides QR, RP are