Tangents PA and PB are drawn to the circle ${(x - 4)}^{2} + {(y - 5)}^{2} = 4$ from the point P on the curve $y = \sin x$ , where A and B lie on the circle. Consider the function $y = f (x)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The period of $y = f (x)$ is

A

$2 π$

B

$3 π$

C

$π$

D

not defined

Text Solution

Verified by Experts

The correct Answer is:3

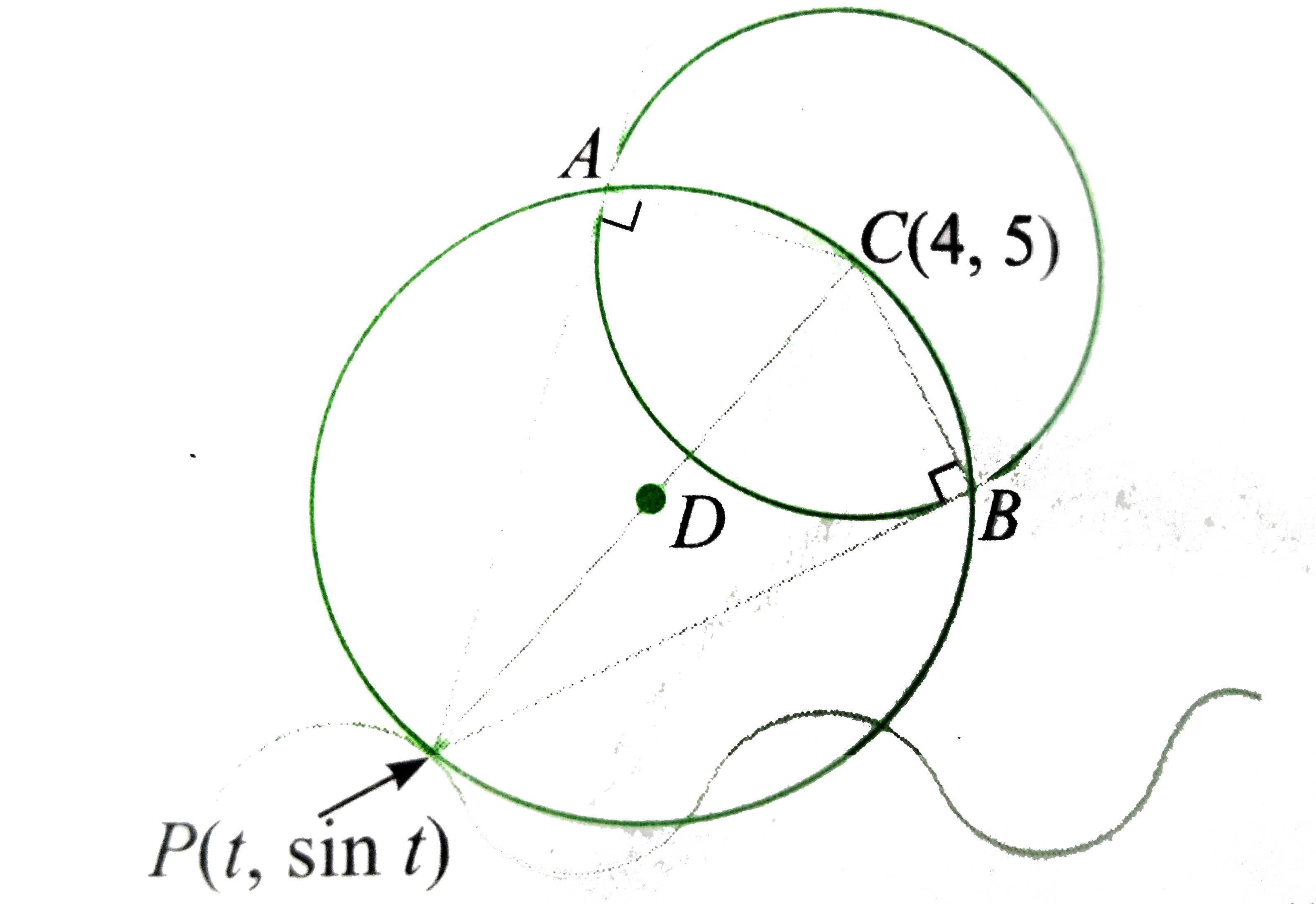
The center of the given circle is $C (4, 5)$ . Points P,A,C, and B are concyclic such that PC is the diameter of the circle. Hence, the center D(h,k) of the circumcircle of $Δ A B C$ is the midpoint of PC.
Then, we have
$h = \frac{t + 4}{2}$ and $k = \frac{\sin t + 5}{2}$
Eliminating t, we have
$k = \frac{\sin (2 h - 4) + 5}{2}$
or $y = f (x) = \frac{\sin (2 x - 4) + 5}{2}$
$∴ f^{- 1} (x) = \frac{\sin^{- 1} (2 x - 5) + 4}{2}$
Thus, the range of
$y = \frac{\sin (2 x - 4) + 5}{2}$
is $[2, 3]$ and the priod is $π$ .
Al,so $f (x) = 4$ , i.e.., $\sin (2 x - 4) = 3$ which has no real solutions.
For $f (x) = 1, \sin (2 x - 4) = 3$ which has no real solutions.
But range of $y = \frac{\sin^{- 1} (2 x - 5) + 4}{2}$ is $[- \frac{π}{3} + 2, \frac{π}{4} + 2]$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Tangents PA and PB are drawn to the circle ${(x - 4)}^{2} + {(y - 5)}^{2} = 4$ from the point P on the curve $y = sin x$ , where A and B lie on the circle. Consider the function $y = f (x)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The range of $y = f (x)$ is
A $[- 2, 1]$
B $[- 1, 4]$
C $[0, 2]$
D $[2, 3]$
Question 2 - Select One
Tangents PA and PB are drawn to the circle ${(x - 4)}^{2} + {(y - 5)}^{2} = 4$ from the point P on the curve $y = sin x$ , where A and B lie on the circle. Consider the function $y = f (x)$ represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?
A $f (x) = 4$ has real roots.
B $f (x) = 1$ has real roots.
CThe range of $y = f^{- 1}$ is $[- \frac{π}{4} + 2, \frac{π}{4} + 2]$
DNone of these
Question 3 - Select One
Tangents PA and PB are drawn to $x^{2} + y^{2} = 4$ from the point $P (3, 0)$ . Area of triangle PAB is equal to:-
A $\frac{10}{9} \sqrt{5}$ sq. units
B $\frac{20}{3} \sqrt{5}$ sq. units
C $\frac{5}{9} \sqrt{5}$ sq. units
DNone of these

CENGAGE-CIRCLE -Exercise (Comprehension)

Home
Ask Doubt
Profile