Complete Solutions to Exercise (Comprehension) of chapter PROPERTIES AND SOLUTIONS OF TRIANGLE of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROPERTIES AND SOLUTIONS OF TRIANGLE |
| CENGAGE NEW | Exercise (Comprehension) |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Given that `Delta = 6, r_(1) = 3, r_(3) = 6`
Circumradius R is equal to03:38View SolutionGiven that `Delta = 6, r_(1) = 3, r_(3) = 6`
Inradius is equal to01:57View SolutionGiven that `Delta = 6, r_(1) = 2,r_(2)=3, r_(3) = 6` Difference between the greatest and the least angles is
06:45View SolutionLet a = 6, b = 3 and `cos (A -B) = (4)/(5)`
Area (in sq. units) of the triangle is equal to04:35View SolutionLet a = 6, b = 3 and `cos (A -B) = (4)/(5)`
Angle C is equal to03:09View SolutionLet a = 6, b = 3 and `cos (A -B) = (4)/(5)`
Value of `sin A` is equal to05:12View SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of `DeltaABC`. Given `AH.CH = 3 and (AH)^(2) + (BH)^(2) + (CH)^(2) = 7`
Then answer the following
Value of `(cos A. cos B : cos C)/(cos^(2)A + cos^(2)B + cos^(2)C)` isView SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of `DeltaABC`. Given `AH.BH.CH = 3 and (AH)^(2) + (BH)^(2) + (CH)^(2) = 7`
Then answer the following
Value of R isView SolutionLet ABC be an acute angled triangle with orthocenter H.D, E, and F are the feet of perpendicular from A,B, and C, respectively, on opposite sides. Also, let R be the circumradius of `DeltaABC`. Given `AH.CH = 3 and (AH)^(2) + (BH)^(2) + (CH)^(2) = 7`
Then answer the following
Value of `HD.HF` isView SolutionLet O be a point inside `DeltaABC` such that
`angleOAB = angleOBC = angle OCA = theta`
`cot A + cot B + cot C` is equal toView SolutionLet O be a point inside `DeltaABC` such that
`angleOAB = angleOBC = angle OCA = theta`
`cosec^(2) A + cosec^(2)B + cosec^(2)C` is equal toView SolutionLet O be a point inside `DeltaABC` such that
`angleOAB = angleOBC = angle OCA = theta`
Area of `DeltaABC` is equal toView SolutionGiven an isoceles triangle with equal side of length b and angle `alpha lt pi//4`, then
the circumradius R is given byView SolutionGiven an isoceles triangle with equal side of length b and angle `alpha lt pi//4`, then
the inradius r is given byView SolutionGiven an isoceles triangle with equal side of length b and angle `alpha lt pi//4`, then
the distance between circumcenter O and incenter I isView SolutionIncircle of `DeltaABC` touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
`angleDEF` is equal toView SolutionIncircle of `DeltaABC` touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
Area of `DeltaDEF` isView SolutionIncircle of `DeltaABC` touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
The length of side EF isView SolutionInternal bisectors of `DeltaABC` meet the circumcircle at point D, E, and F
Length of side eF isView SolutionInternal bisectors of `DeltaABC` meet the circumcircle at point D, E, and F
Area of `DeltaDEF` is03:30View SolutionInternal bisectors of `DeltaABC` meet the circumcircle at point D, E, and F
Ratio of area of triangle ABC and triangle DEF isView SolutionThe area of any cyclic quadrilateral ABCD is given by `A^(2) = (s -a) (s-b) (s-c) (s-d)`, where `2s = a + b ++ c + d, a, b, c and d` are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is01:47View SolutionThe area of any cyclic quadrilateral ABCD is given by `A^(2) = (s -a) (s-b) (s-c) (s-d)`, where `2s = a + b ++ c + d, a, b, c and d` are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minimum value of the sum of the lenghts of diagonals is02:32View SolutionThe area of any cyclic quadrilateral ABCD is given by `A^(2) = (s -a) (s-b) (s-c) (s-d)`, where `2s = a + b ++ c + d, a, b, c and d` are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily01:45View SolutionIn `DeltaABC, R, r, r_(1), r_(2), r_(3)` denote the circumradius, inradius, the exradii opposite to the vertices A,B, C respectively. Given that `r_(1) :r_(2): r_(3) = 1: 2 : 3`
The sides of the triangle are in the ratio03:14View SolutionIn `DeltaABC, R, r, r_(1), r_(2), r_(3)` denote the circumradius, inradius, the exradii opposite to the vertices A,B, C respectively. Given that `r_(1) :r_(2): r_(3) = 1: 2 : 3`
The value of `R : r` is04:58View SolutionIn `DeltaABC, R, r, r_(1), r_(2), r_(3)` denote the circumradius, inradius, the exradii opposite to the vertices A,B, C respectively. Given that `r_(1) :r_(2): r_(3) = 1: 2 : 3`
The greatest angle of the triangle is given by03:39View SolutionIn `DeltaABC, P,Q, R` are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. `DeltaPQR` is constructed

If `angleBAC = 120^(@)`, then measusred of `angleRPQ` will beView SolutionIn `DeltaABC, P,Q, R` are the feet of angle bisectors from the vertices to their opposite sides as shown in the figure. `DeltaPQR` is constructed
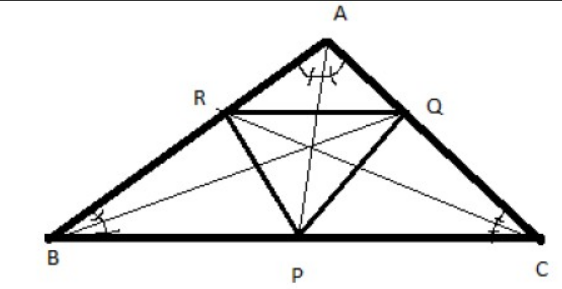
If `AB = 7` units, BC = 8 units, AC = 5 units, then the side PQ will beView SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If `BC = 6, AC = 8`, then the length of side AB is equal toView SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If `angleGAC = (pi)/(3) and a = 3b`, then sin C is equal toView SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If AC = 1, then the length of the median of triangle ABC through the vertex A is equal toView SolutionThe inradius in a right angled triangle with integer sides is r
If r = 4, the greatest perimeter (in units) isView SolutionThe inradius in a right angled triangle with integer sides is r
If r = 5, the greatest area (in sq. units) isView Solution
Exercise (Comprehension) questions and complete solutions for chapter PROPERTIES AND SOLUTIONS OF TRIANGLE of CENGAGE MATHS (HINGLISH) of Class 12
