Complete Solutions to Exercises Subjective of chapter ELECTROMAGNETIC INDUCTION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ELECTROMAGNETIC INDUCTION |
| CENGAGE PHYSICS | Exercises Subjective |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
A long thin wire carrying a varying current `I = i_(0) sin omegat` lies at a distance `y` above one edge of a rectangular wire loop of length `L and W` lying in the `x-z` plane. What emf is induced in the loop?

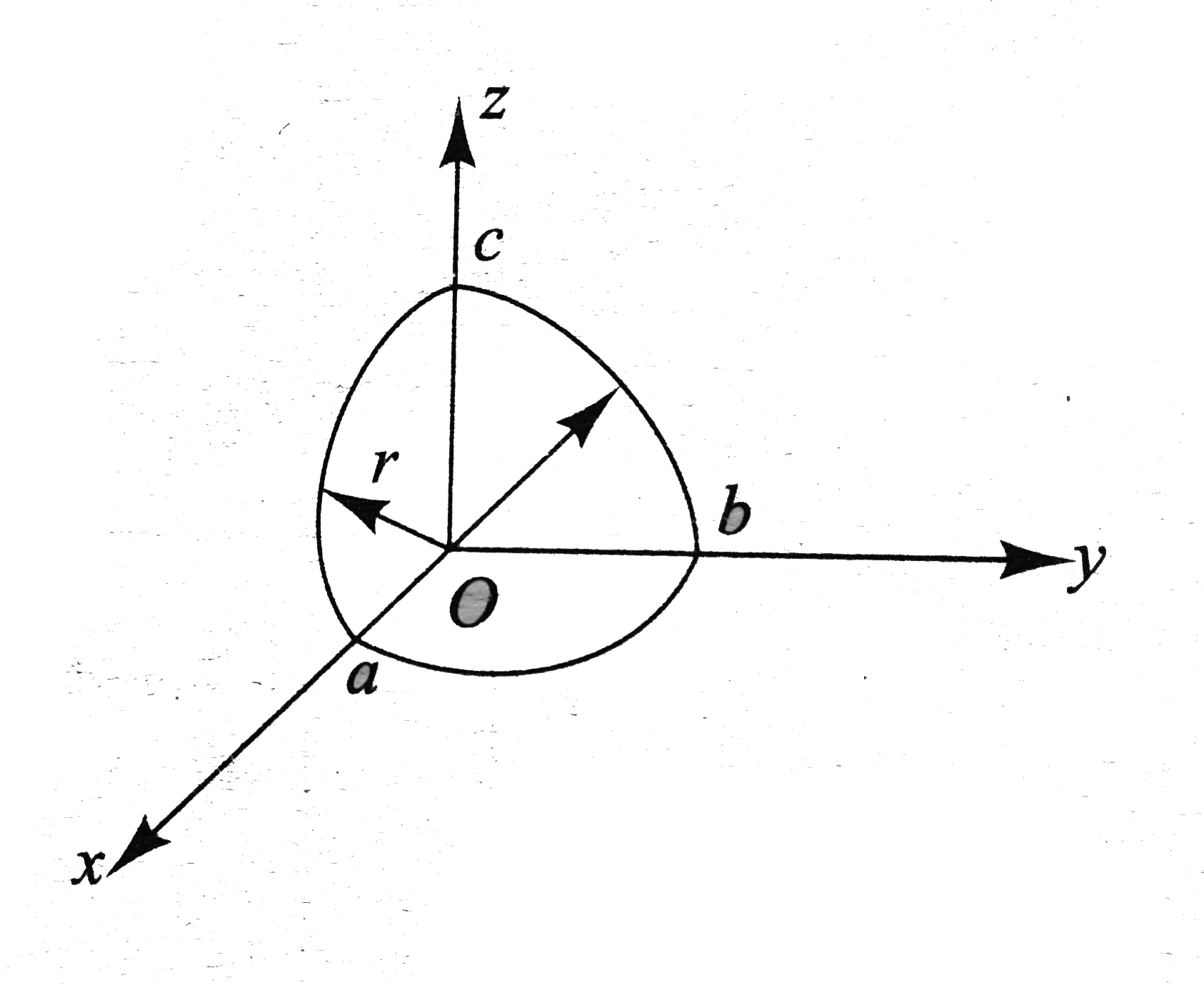
View SolutionA wire is bent into three circular segment of radius `r = 10 cm` as shown in. Each segment is a quadrant of a circle `ab` lying in the `x-y` plane, `bc` lying in the `y-z` plane and `ca` lying in the `z-x` plane.
(a) if a magnetic field `B` points in the positive `x` direction, what is the magnitude of the emf developed in the wire when `B` increases at the rate of `3 mTs^(-1)`?
(b) What is the direction of teh current in the segment `bc`.
View SolutionThree identical wires are bent into semi-circular arcs to each of radius `R`. These arcs are connected with each other to form a closed mesh such that one of tham lies in `x-y` plane, one in `y-z` plane and the other in `z-x` plane as shown in. In the region of space, a uniform magnetic field of induction `vec(B) = B_(0)(hat(i) + hat(j))` exists, whose magnitude increases at a constant rate `dB//dt = alpha`. Calculate the magnitude of emf induced in the mesh and mark the direction of flow of induced current in the mesh.

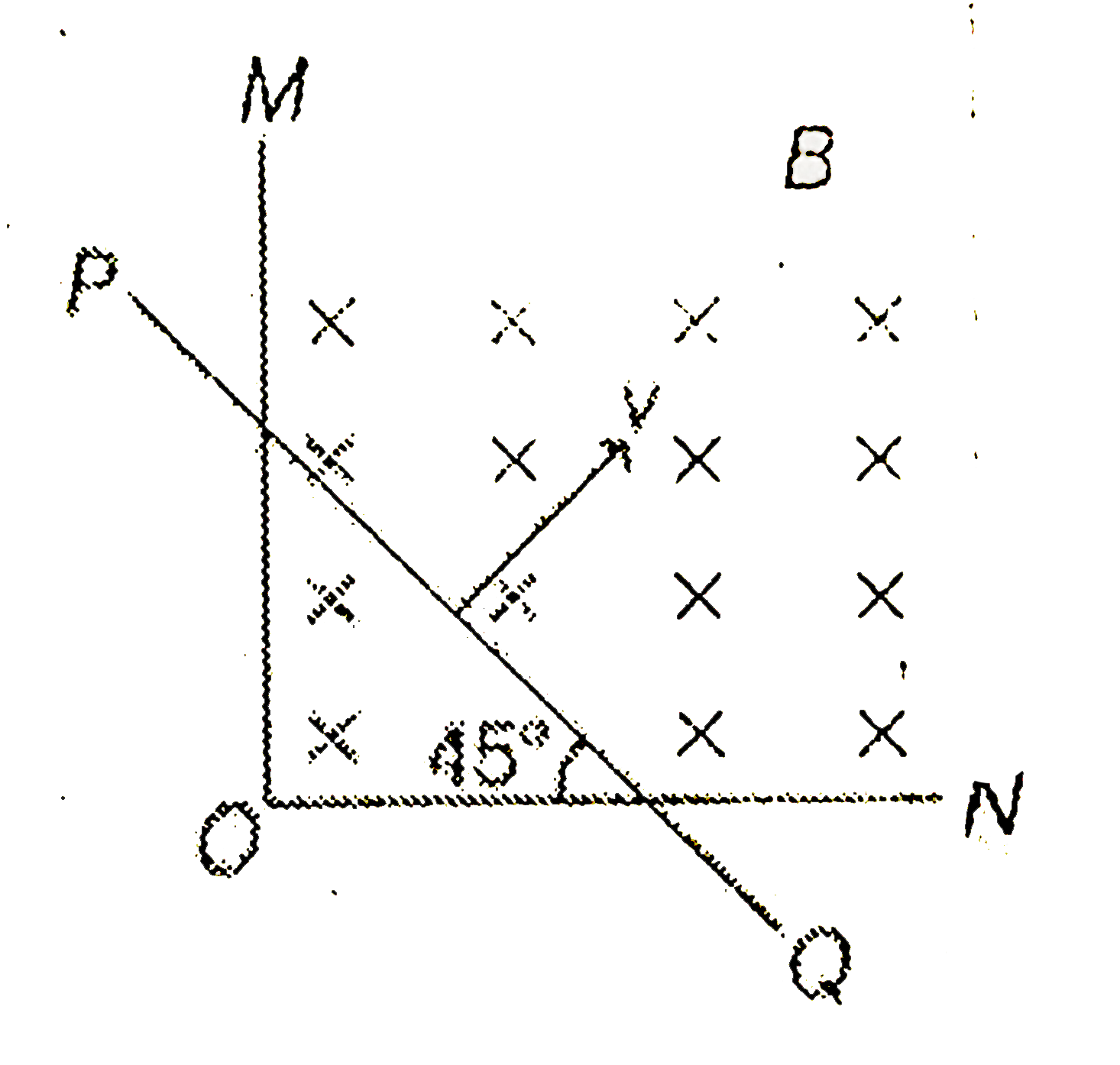
View SolutionElectric circuit is composed of three conducting rods MO, ON and PQ as shown in the figure. The resistance of the rods per unit length is known to be 1. The rod PQ slides as shown in the figure. At t=0, rod PQ is at O. The whole system is embledded ina uniform magnetic field B, which is directed perpendicularly into page. The induced electric current is:
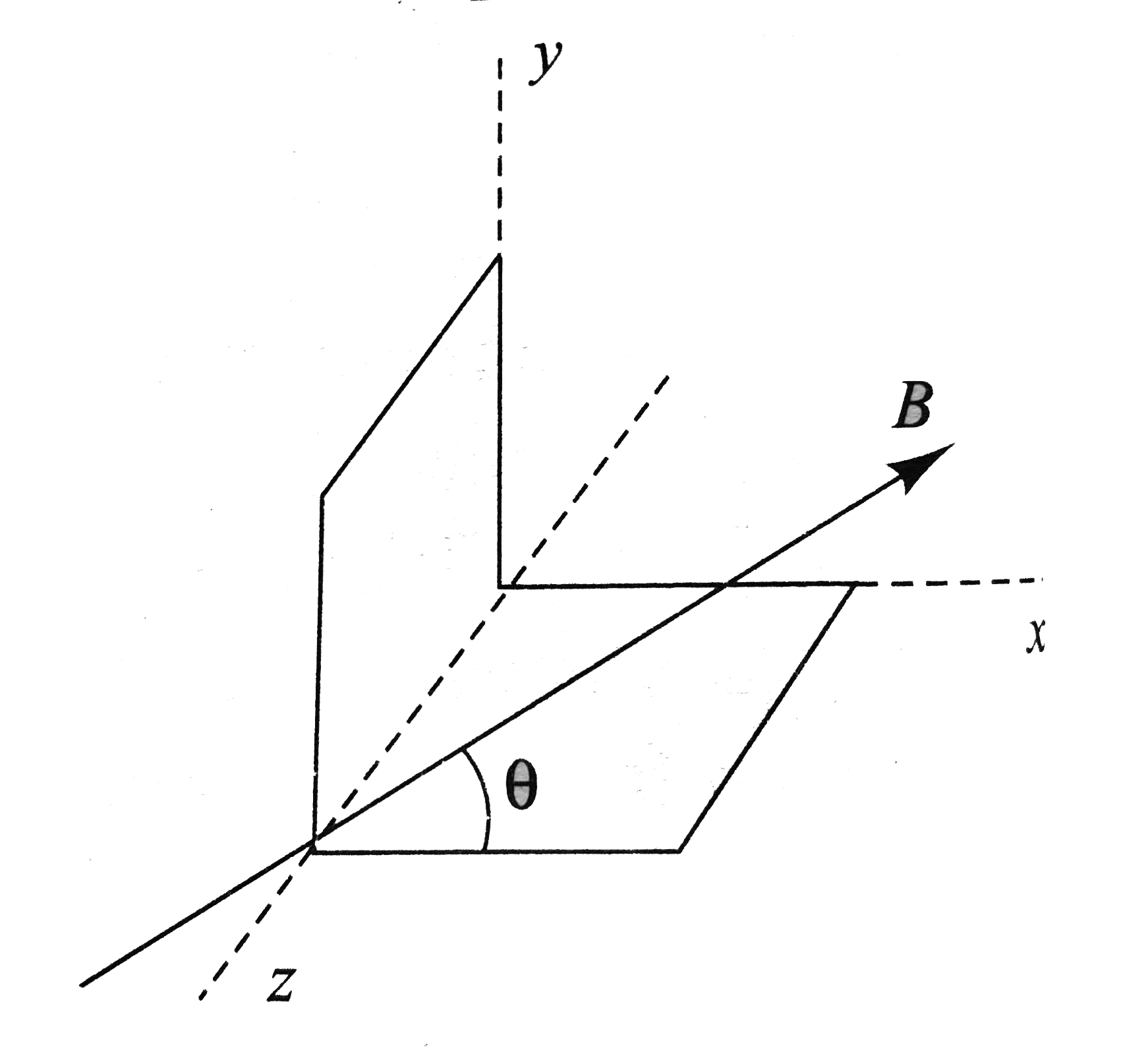
View SolutionThe wire loop, shown in , is made by taking a flat rectangular loop of sides `10 cm` and `20 cm` bending at the long sides a their midpoints to produce two mutually perpendicular square parts. The loop is laced in an oscillating magnetic field `B = B_(0) sin2pivt`, with `B_(0) = 1.2 xx 10^(-3) T` and `v = 60 Hz`. The magnetic field is induced at angle `theta` with `x-z` plane.
(a) Express the emf around the loop as a function of time and the angle `theta`.
(b) For what angle `theta` does the induced emf have the largest amplitude ?
View SolutionA rod of mass `m` can rotate without friction about axis sliding (also without friction) along a conducting ring of radius `b` arranged in a vertical plane as shown in the . The entire arrengement is placed in a uniform magnetic field with the inducetion `B` perpendicular to the plane of the ring. The axis and the conductor are connected to teh terminals of a current source. Determine
(a) according to which law current `I` flowing in the rod must vary for the rod to rotate at a constant angular speed. Being to measure the time from the instant when the rod is in its right-hand horizontal position. Consider the current to be positive when it flows from the axis of rotation toward the ring.
(b) what emf `E` of the source must be applied to maintain the required current? Consider the total resistance of the circuit to be constant and equal to `R`. Disergard the inductance of teh circuit.

View SolutionA square shaped, conducting wire loop of side `L`, total mass `m` and total resistance `R` initially lies in the horizontal `x-y` plane, with corners at `(x, y, z) = (0,0,0), (0, L , 0), (L, 0 ,0), and (L, L, 0)`. There is a uniform upward magnetic field in the space within and around the loop. The side of the loop that extends from `(0, 0, 0)to (L, 0, 0)` is held in place on the x-axis, the rest of the loop is released, it begins to rotate due to the gravitational torque.
(a) Find the net torque (magnitude and direction)that acts on the loop when it has rotated through an anglr `phi` from its original orientation and is rotating dounward at an angular speed `omega`.
(b) Find the angular acceleration of the loop at the instant described in part (a).
( c) Compared to teh case with zero magnetic field, does it take the loop a longer or shorter time to rotate through `90^(@)` ? Explain.
(d) Is mechanical energy conserved as the loop rotates downward ? Explain.
View Solution`CDEF` is a fixed conducting smooth frame in vertical plane. A conducting uniform rod `GH` of mass `m` can move vertically and smoothly without losing contact with the frame. `Gh` always remains horizontal and is given velocity `u` upward and released. Taking the acceleration due to gravity as `g` and present other than `R`. Find out the time tasken by the rod to reach the highest point.

View SolutionThe entire network shown here, has uniform wire having resistance per unit length `1Omega//m`. It is place in a uniform but time varying magnetic field (directed into the plane). If magnetic field increasing at a rate of IT/s, the ratio `I_(1)//I_(2)` equals

View SolutionTwo fixed long straight wires carry the same current `i` in opposite directions as shown in . A square loop of side `b` is fixed in the plane of the wires with its length parallel to one wire at a distance a shown in the figure.

(a) alculate at the induced emf in the loop if the current in both the wires is changing at the rate `di//dt`.
(b) What is the direction of force on the loop if `di//dt` is positive?
View SolutionTwo parallel, long, straight conductor lie on a smooth plane surface. Two other parallel so as to form a square of side a initially. A uniform magnetic field `B` exists at right angles to the plane containing the cinductors. Now they start moving out with a constant velocity `v`.
(A) Will the induced emf be time dependent?
(b) Will the current be time dependent ?
View SolutionThe rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity `v_0`. (c) show that the velocity at tiem t is given by ` v= v_0(1 - e^(-(Ft)/(mv_0)))`.
(##HCV_VOL2_C38_E01_083_Q01##)
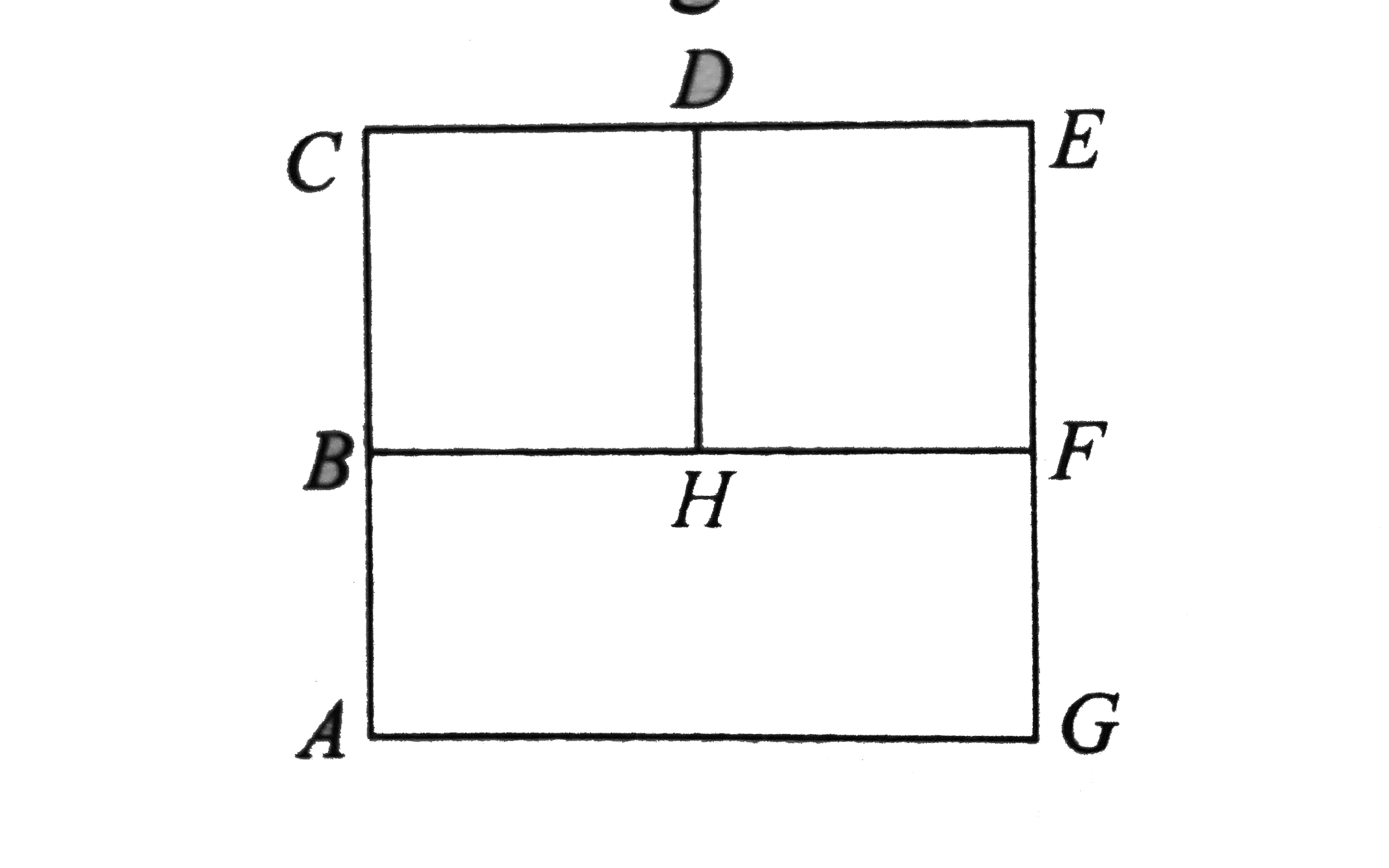
View Solution, `ABCEFGA` is a square conducting frame of side `2 m` and resistance `1 Omega m^(-1)`. A uniform magnetic field `b` is applied perpendicular to the plane and pointing inward. It increases with time at a constant rate of `10 T s^(-1)`. Find the rate at which heat is produced in the circuit, `AB = BC = CD = BH`.
View Solution
Exercises Subjective questions and complete solutions for chapter ELECTROMAGNETIC INDUCTION of CENGAGE PHYSICS (ENGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS ELECTROMAGNETIC INDUCTION
- Archives Asserton - Reasoning
- Archives Fill In The Blanks
- Archives Multiple Correct
- Archives Single Correct
- comprehensive
- comprehensive type
- compression type
- Exercise 3.1
- Exercise 3.2
- Exercises Asserton - Reasoning
- Exercises Integer
- Exercises Linked Comprehension
- Exercises Multiple Correct
- Exercises Single Correct
- Exercises Subjective
- Illustration
- Multiple correct Answer Type
- single correct
- single correct
- single correct answer
- Single Correct Answer Type
- Solved Example