Complete Solutions to Illustration of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
An electron in a hydrogen atom makes a trsnsition `n_(1)rarrn_(2)` where `n_(1)` and `n_(2)` are principal quantum numbers of the two states. Assume the Bohr model to be valid. The time period of the electron in the initial state is eight times that in the final state. The possible values of `n_(1)` and `n_(2)` are
View SolutionHow many time does the electron go round the first bohr orbit of hydrogen atoms in `1 s`?
View SolutionWhat is the angular momentem of an electron in Bohr's hydrogen atom whose energy is `- 3.5eV`?
View SolutionIf the average life time of an excited state of hydrogen is of the order of `10^(-8) s`, estimate how many rotations an electron makes when it is in the state `n = 2` and before it suffers a transition to state` n = 1 (Bohr radius a_(0) = 5.3 xx 10^(-11)m)`?
View SolutionConsider energy level diagram of a hydrogen atom.How will the kinetc energy and potential energy of electron moves from a lower level to a higher level?
View SolutionSoppose potential energy between electronand proton at seperation `r` is given by `U = klog r, where k` is a constant. For such a hypothetical hydrogen atom , calculate the radins of nth Bohr and its energy level
View SolutionDetermine the minimum wavelength of a photon the can cause ionization of He ^(+) ion.
View SolutionFind the quantum number `n` corresponding to the excited state of He^(+) ion if on transition to the ground state that ion emits two photons in succession with wavelengths state that ion emits two photons in succession with wavelengths`1026.7 and 304Å. (R = 1.096 xx 10^(7)m^(_1)`
View SolutionA gas of hydrogen like atoms can absorb radiation of 68 eV. Consequently, the atom emits radiations of only three different wavelengths. All the wavelengths are equal or smaller than that of the absorbed photon.
(a) Determine the initial state of the gas atoms.
(b) Identify the gas atoms. (c ) find the minimum wavelength of the emitted radiations.
(d) Find the ionization energy and the respective wavelength for the gas atoms.
View SolutionFind the ratio of ionization energy of bohr 's hydrogen atom doubly liothium ion `(Li^(2))`
View SolutionThe Bohr moden does not apply when more than one electron orbit the nucleues because it does not account for the electrostatic force that the electron exert on one another.For instance , an electrically neutral lithium atom `(Li)` contains three electrons in orbit around a nucleus that includes three protons `(Z = 3)`, and Bohr's model can be used for the doubly charged positive ion of lithium `(Li^(2)^(+))` that results when two electrons are removed from the neutral atom, leaving only one electron to orbit the nucleus . Obtain the ionization energy that is needed to remove the remaining electron from `(Li^(2)^(+))`
View SolutionThe energy levels of a hypothetical one electron atom are given by `E_n = -(18.0)/(n^2) eV`
where n = 1,2,3,…. (a) Compute the four lowest energy levels and construct the energy level diagram.
(b) What is the first excitation potential
(c ) What wavelength (Å) can be emitted when these atoms in the ground state are bombarded by
electrons that have been accelerated through a potential difference of 16.2 V?
(d) If these atoms are in the ground state, can they absorb radiation having a wavelength of 2000 Å ?
(e) what is the photoelectric threshold wavelength of this atom?
View SolutionA doubly ionized lithium atom is hydrogen like with atomic number 3. Find the wavelength of the radiation required to excite the electron in `Li^(++)` from the first to the third Bohr orbit (ionization energy of the hydrogen atom equals 13.6 eV).
View SolutionA single electron orbit around a stationary nucleus of charge `+ Ze` where Z is a constant and e is the magnitude of the electronic charge. It requires`47.2 eV` to excite the electron from the second bohr orbit to the third bohr orbit. Find
(i) The value of Z
(ii) The energy required by nucleus to excite the electron from the third to the fourth bohr orbit
(iii) The wavelength of the electronmagnetic radiation required to remove the electron from the first bohr orbit to inlinity
(iv) The energy potential energy potential energy and the angular momentum of the electron in the first bohr orbit
(v) The radius of the first bohr orbit (The ionization energy of hydrogen atom ` = 13.6 eV ` bohr radius `= 5.3 xx 10^(-11) matre` velocity of light `= 3 xx 10^(8) m//sec` planks 's constant ` = 6.6 xx 10^(-34)` jules - sec )
View SolutionIn atension of state `n` from a state of excitation energy given is `10.19 eV`, hydrogen atom emits a photon with wavelength `4890 Å` . Determine the binding energy of the initial state.
View SolutionThe first excitation potential of a hypothetical hydrogen- like atom is `15 V`. Find the third excitation potential of the atom.
View SolutionThe energy level excitation potential of a hydrogen -like atom is shown in Figure

a Find the value of `Z`
b If initially the atom is in the ground state ,then
(i) determine its excitation potential, and
m (ii) determine its ionization potential.
c Can it absorbe a photom of `42 eV`?
d Can it absorbe a photom of `56 eV`?
e Calculate the radius of its first Bohr orbit.
f Calculate the kinectic and potential energy of an electron in the first orbit.
View SolutionBrackett series of lines are producted when electrons excited t high energy level make transitions to the `n = 4` level.
a Determine the longest wavelength in this series.
b Determine the wavelength that corresponds to the transition from `n_(f) = 6 to n_(i) = 4`.
View SolutionElectrons of energy `12.09 eV` can excite hydrogen atoms . To which orbit is the electron in the hydrogen atom raisd and what are the wavelengths of the radiations emitted as it dropes back to the ground state?
View SolutionA hydrogen atom is in the third excited state. It make a transition to a different state and a photon is either obsorbed or emitted. Determine the quantum number `n` of the final state and the energy energy of the photon If it is
a emitted with the shortest possible wavelength.
b emitted with the longest possible wavelength and
c absorbed with the longest possible wavelength.
View SolutionThe Bamber series for the hydrogen atom corresponds to electron that terminal in the state of quantum number `n = 2`.
a Find the longest wavelength photon emitted and determine its energy.
b Find the shortest wavelength photon emitted in the balmer series.
View SolutionHow many different wavelengths may be observed in the spectrum from a hydrogen sample if the atoms excited to states with principal quantum number n?
View SolutionA positronium "atom" is a system that consists of a positron and an electron that orbit each other. Campare the wavelengths of the spectral lines of positronium with those of ordinary hydrogen.
View SolutionA `muon` is an unstable elementary particle whose mass is `207 m_e` and whose charge is `either^+ e` or `-_e`. A negative muon `(mu-1)` can be captured by a nucleus to form a muonic atom.
(a) A proton captures a `mu^-`. Find the radius of the first Bohr orbit of this atom.
(b) Find the ionization energy of the atom.
View SolutionA particle known as mu meson has a charge equal to that of no electron and mass `208`times the mass of the electron B moves in a circular orbit around a nucleus of charge `+3e` Take the mass of the nucleus to be infinite Assuming that the bohr's model is applicable to this system (a)drive an expression for the radius of the nth Bohr orbit (b) find the value of a for which the radius of the orbit it appropriately the same as that at the first bohr for a hydrogen atom (c) find the wavelength of the radiation emitted when the u - mean jump from the orbit to the first orbit
View SolutionA neutron which is going to collde head on to a stationary `H` atom has intial kinetic energy of `24.5 eV`. Discuss different possibilites of collsion.
View SolutionIn the figure , what type of collision can be possible , if `K = 14 eV, 20.4 eV,22 eV, 24.18 eV,(elastic // inelastic // perfectly inelastic).
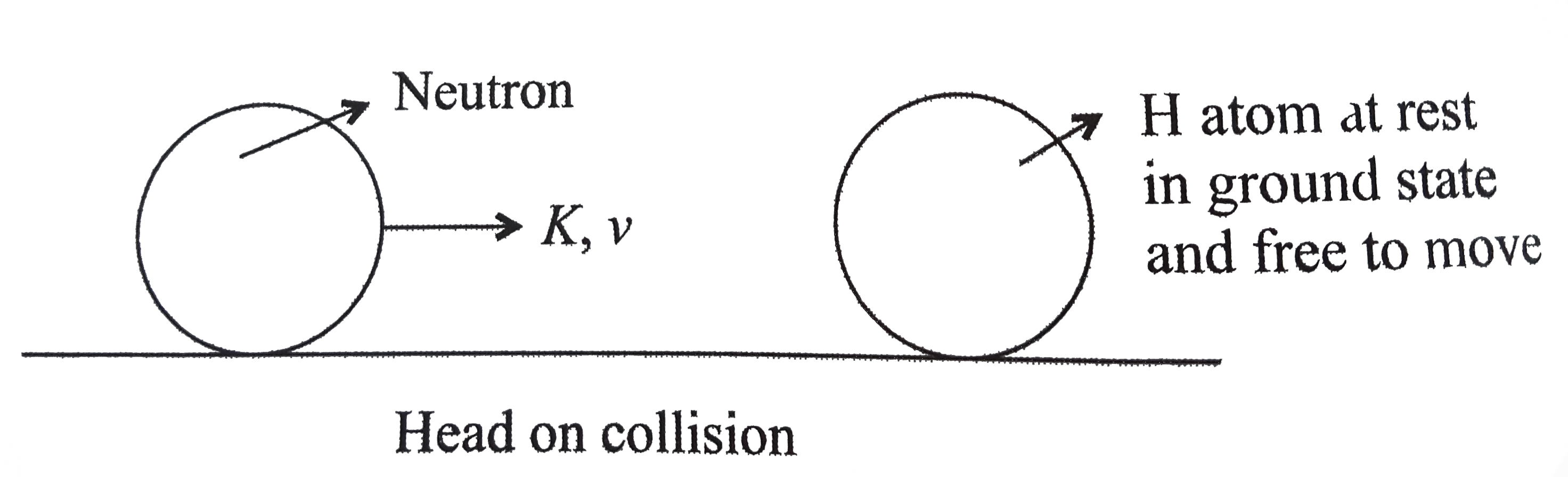
View SolutionA `He^(+)` ion is at rest and is in ground state. A necutron with intial kinetic energy`K` collides heads on with the `He^(+)` ion. Find minimum value of `K` so that there can be an inelastic collision between these two particals.

View SolutionIn the previous question , find minimum value of `K` so that all types of collisions are piossible.
View SolutionA `He^(+)` ion is at rest and is in ground state. A necutron with intial kinetic energy`K` collides heads on with the `He^(+)` ion. Find minimum value of `K` so that there can be an inelastic collision between these two particals.

View SolutionA moving hydrogen atom makes a head on collision with a stationary hydrogen atom. Befor collision both atoms are in in ground state and after collision they move together. The minimum value of the kinetic energy of the moving hydrogen atom, such that one of the atoms reaches one of the excitation state is
View SolutionA neutron with an energy of `4.6 MeV` collides elastically with proton and is retarded. Assuming that upon each collision the neutron is deflected by `45^(@)`, find the number of collisions which will reduce its energy to `0.23 eV`.
View SolutionExplain why nearly all `H` atoms are in the ground state at room temperature and hence emit no light.
View SolutionConsider a hydrogen-like atom whose energy in nth excited state is given by
`E_(n) = - (13.6 Z^(2))/(n^(2))`
When this excited makes a transition from excited state to ground state , most energetic photons have energy
`E_(max) = 52.224 eV`. and least energetic photons have energy
`E_(min) = 1.224 eV`
Find the atomic number of atom and the initial state or excitation.
View SolutionA gas of identical hydrogen-like atoms has some atoms in the lowest in lower (ground) energy level `A` and some atoms in a partical upper (excited) energy level `B` and there are no atoms in any other energy level.The atoms of the gas make transition to higher energy level by absorbing monochromatic light of photon energy `2.7 e V`.
Subsequenty , the atom emit radiation of only six different photon energies. Some of the emitted photons have energy `2.7 e V` some have energy more , and some have less than `2.7 e V`.
a Find the principal quantum number of the intially excited level `B`
b Find the ionization energy for the gas atoms.
c Find the maximum and the minimum energies of the emitted photons.
View SolutionA hydrogen like atom (atomic number Z) is in a higher excited state of quantum number n. The excited atom can make a transition to the first excited state by successively emitting two photons of energy 10.2 eV and 17.0 eV, respectively. Alternatively, the atom from the same excited state can make a transition to the second excited state by successively emitting two photons of energies 4.25 eV and 5.95 eV, respectively Determine the values of n and Z. (lonization energy of H-atom = 13.6 eV)
View SolutionElectrons in hydrogen like atoms (Z = 3) make transitions form the fifth to the fourth orbit and from the fourth to the third orbit. The resulting radiations are incident normally on a metal plate and eject photoelectrons. The stopping potential for the metal and the stopping potential for the photoelectrons ejected by the longer wavelength.
View SolutionThe radiation emitted when an electron jumps from `n=3` to `n=2` orbit of hydrogen atom falls on a metal to produce photoelectrons. The electrons emitted from the metal surface with maximum kinetic energy are made to move perpendicular to a magnetic field of `(1)/(320)` T is a radius of `10^-3m`. Find:
A. the kinetic energy of the electrons,
B. work function of metal, and
C. wavelength of radiation.
(Planck's constant `h=6.62xx10^-32J-s`)
View SolutionAn X-ray tube operates at 20 kV. A particular electron loses 5% of its kinetic energy to emit an X-ray photon at the first collision. Find the wavelength corresponding to this photon.
View SolutionAn X-ray tube operates at `20k V`. Find the maximum speed of the electron strinking the anode , given the charge of electron is `1.6 xx 10^(-19)` coulomb and mass of electron is `9 xx 10^(-31) kg`.
View SolutionA voltage applied to an X-ray tube being increased `eta = 1.5` times, the short wave limit of an x-ray continuous spectrum shifts by `Delta lambda= 26 `pm`.` Find the initial voltage applied to the tube.
View SolutionIn figure find which is `K_(a) and K_(beta)`

View SolutionIn figure find which is `K_(a) and L_(alpha')`

View SolutionThe `K_(alpha)` X-ray emission line of tungsten occurs at `lambda = 0.02 nm`. The energy difference between `K and L` level in this atom is about
View SolutionWhen `0.50` Å X-ray strike a material , the photoelectron from the `K` shell are observed to move in a circle of radius `2.3 nm` in a magnetic field of `2 xx 10^(-2)` tesle acting perpendicular to direct of emission of photoelectron . What is the binding elergy of `k-shell` electron?
View SolutionIf the `K_alpha` radiation of `Mo (Z = 42)` has a wevelength of `0.71Å`, calculate wevelength of the corresponding radiation of `Cu,i.e. , k_(alpha)for Cu (Z = 29)` assuming b = 1.
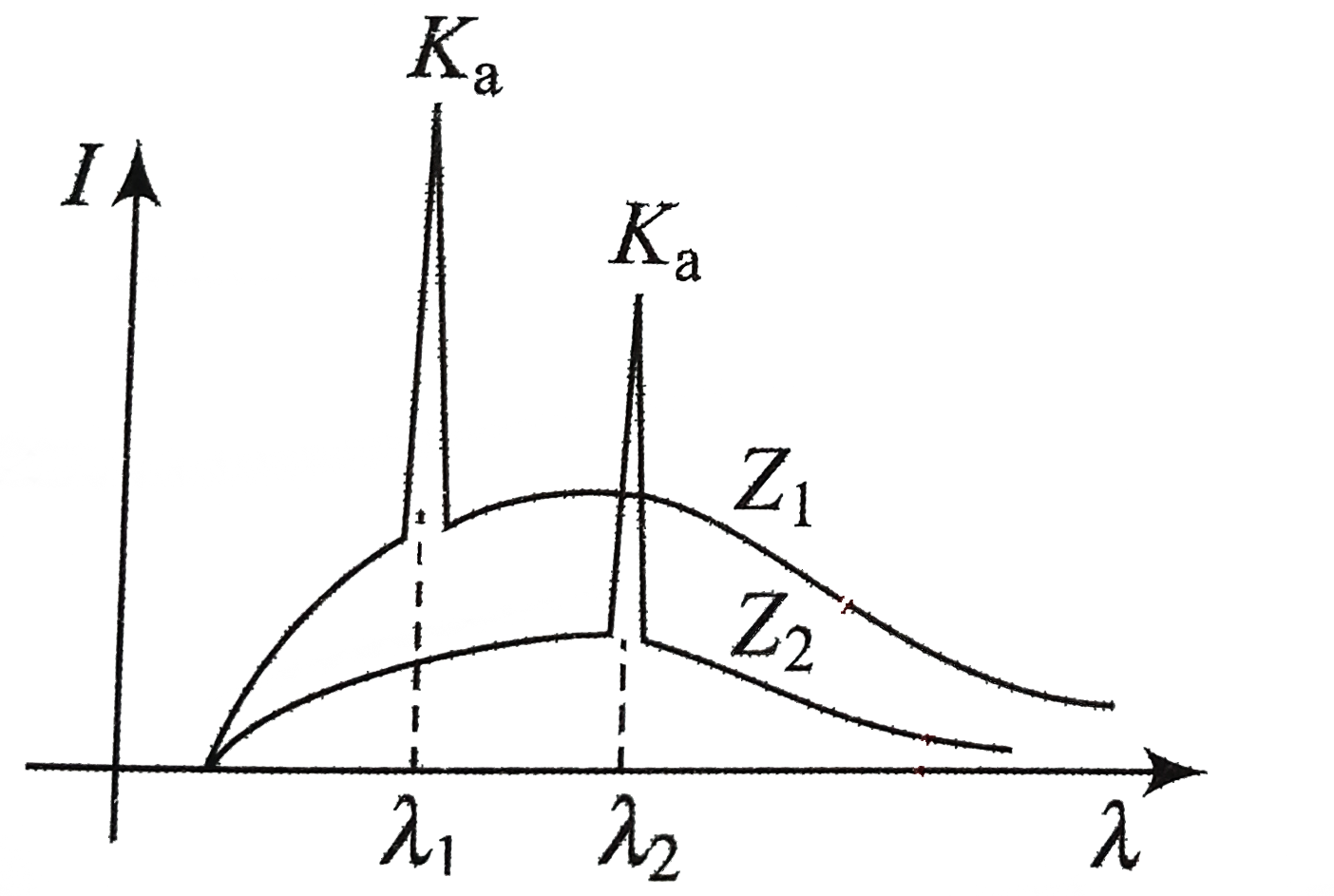
View SolutionCompare `Z_(1) and Z_(2)`
View SolutionA cobalt target `(Z = 27)` is bomberded with electron and the wavelength of its characteristic spectrum are measured . A second , fainter characcteristic spectrum is also found because of an impurity in the target. The wevelength of the `K_(alpha)` lines are 178.9 pm (cobalt) and `143.5 pm` (impurity). What is the impurity?
View SolutionAn X-ray tube with a copper target is found to be emiting lines other than those due to copper. The `K_(alpha)` line of coper is known to have a wavelength `1.5405 Å` and the other two `K_(alpha)` lines observed have wavelengths `0.7090 Å and 1.6578 Å` Identify the impurities.
View SolutionThe `K`-absorption edge of an unknown element is `0.171 Å`
a. Identify the element.
b. Find the average wavelength of the `K_(alpha),K_(alpha),K_(beta),K_(gamma)` lines.
c.
If a `100 e V` electron strikes the target of this element , what is the minimum wavelength of the x-ray emitted?
View Solution
Illustration questions and complete solutions for chapter ATOMIC PHYSICS of CENGAGE PHYSICS (ENGLISH) of Class 12