The energy levels of a hypothetical one electron atom are given by En=−18.0n2eV
where n = 1,2,3,…. (a) Compute the four lowest energy levels and construct the energy level diagram.
(b) What is the first excitation potential
(c ) What wavelength (Å) can be emitted when these atoms in the ground state are bombarded by
electrons that have been accelerated through a potential difference of 16.2 V?
(d) If these atoms are in the ground state, can they absorb radiation having a wavelength of 2000 Å ?
(e) what is the photoelectric threshold wavelength of this atom?
a. E1=−18.012=−18.0eV,E2=−18.022=−4.5eV,
E_(3) = - (18.0)/(3^(2)) = - 2.0 eV, E_(4) = - (18.0)/(4^(2)) = - 1.125 e V<br>Thee≠rgy≤veldiagramisshow∈g∈figure<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V04_C04_S01_012_S01.pngwh=80%mx-autosty≤=background:white;><br>b.Theexcitationpotentialofstaten = 2is:<br>18.0 - 4.5 = 13.5 V<br>c.E≠rgyofthee≤ctronae≤ratedbyapotentiald⇔erenceof16.2 eV.Withthise≠rgythee≤ctroncanexcitethea→momn = 3as<br>E_(4) - E_(1) = 1.125 - (- 18.0) = 16.875 e V gt 16.2 e V<br>E_(3) - E_(1) = 2.0 - (- 18.0) = 16.0 e V lt 16.2 e V<br>lambda_(32) = (12375)/(E_(3) - E_(2)) = (12375)/(- 2.0 - (- 4.5)) = 4950 Å<br>lambda_(31) = (12375)/(E_(3) - E_(2)) = (12375)/(16) = 773 Å<br>andlambda_(21) = (12375)/(E_(2) - E_(1)) = (12375)/(- 4.5 - (- 18.0)) = 917 Å<br>d.Nothee≠rgycorrespond∈g→lambda = 2000 Å<br>E = (12375)/(2000) = 6.187.5 Å<br>Theminiμmcxcitatione≠rgyis13.5 e V (n = 1) to n = 2)).<br>e.Thresholdweve≤n>hforpho→emission→takeplaceomsuchana→mislambda_(max) = (12375)/(18) = 687.5 Å
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Solved Examples
23 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise 4.1
15 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Single Correct
10 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
Similar Questions
The energy levels of a hypothetical one electron atom are given by En=−18.0n2eV
where n = 1,2,3,…. (a) Compute the four lowest energy levels and construct the energy levels diagram. (b) What is the first excitation potential (c ) What wavelength (Å) can be emitted when these atoms in the ground state are bombarged by electrons that have been accelerated through a potential difference of 16.2 V? (e) what is the photoelectric threshold wavelength of this atom?
View SolutionThe energy levels of a hypothetical one electron atom are shown in figure
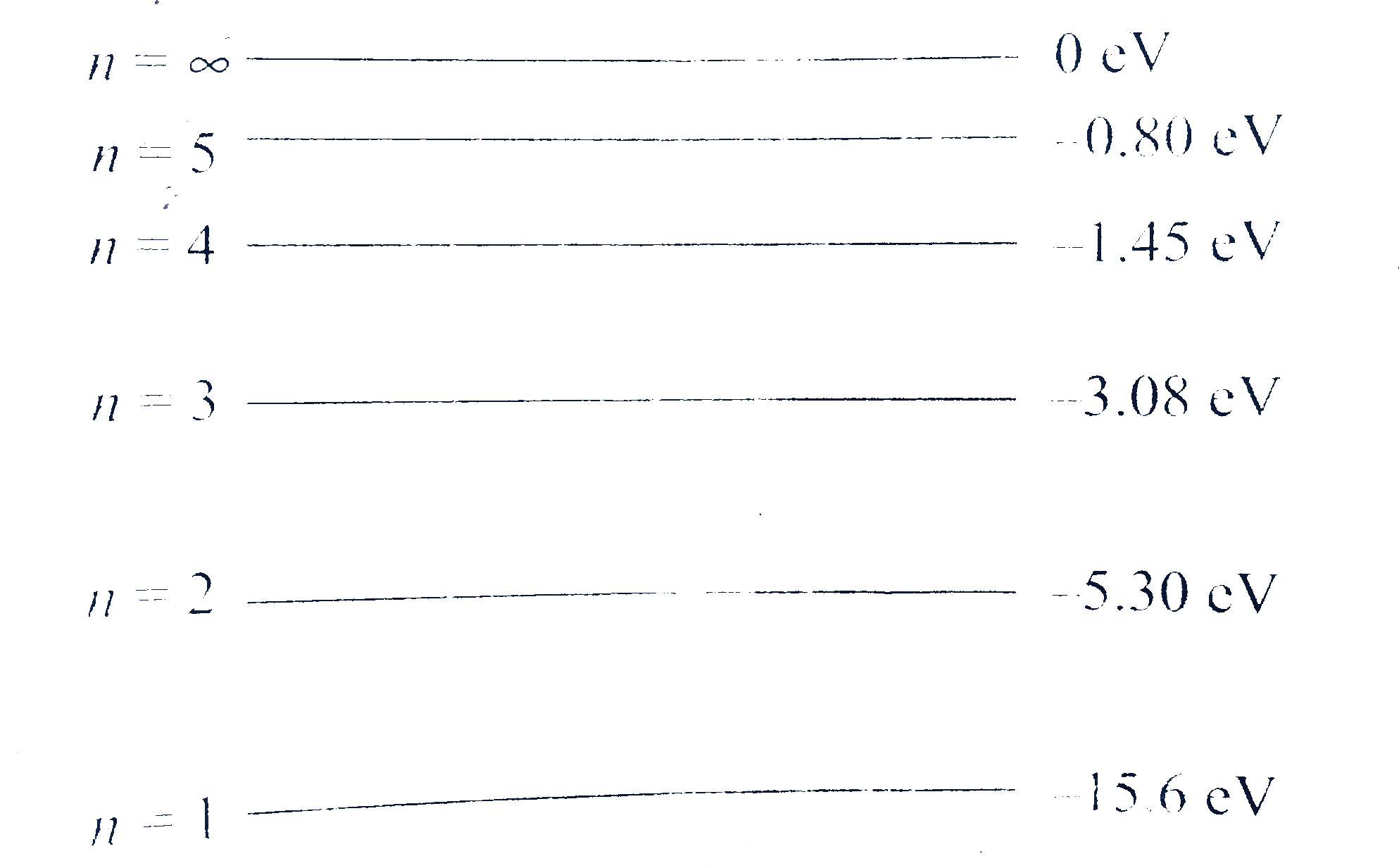
Find the ionization potential of the atom.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
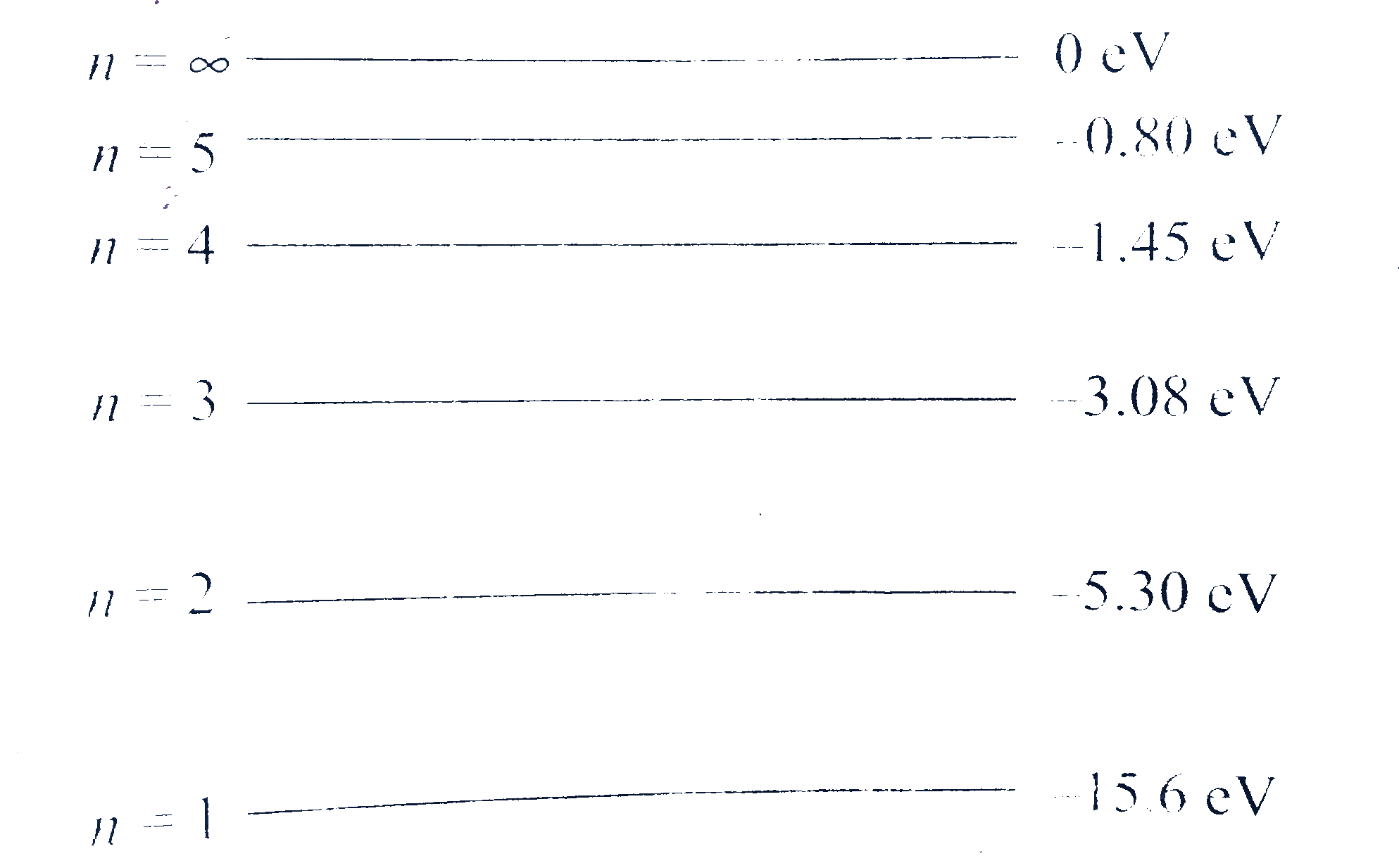
Find the excitation potential for the state n=3.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
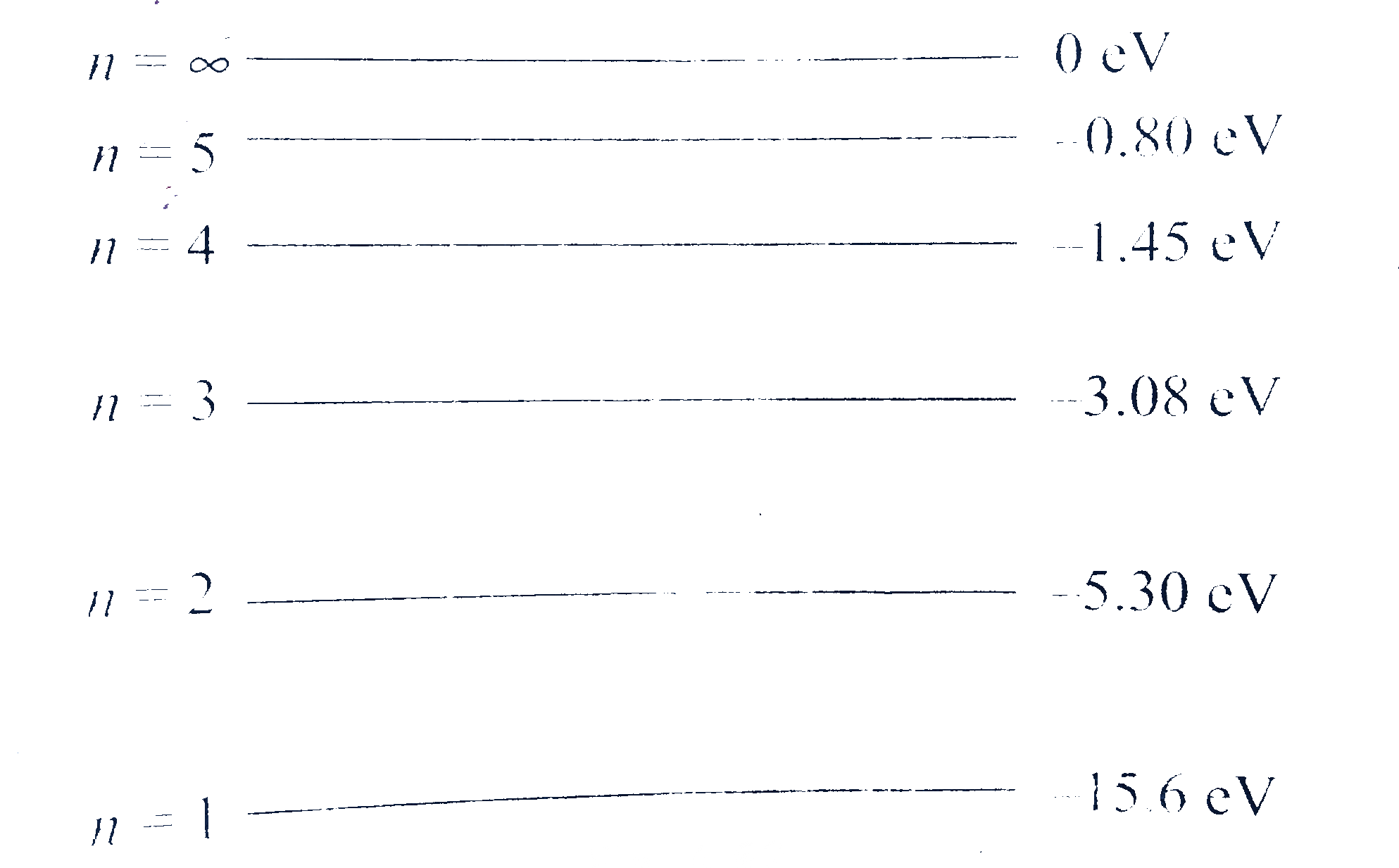
Find the short wavelength limit of the series terminating at n=2.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
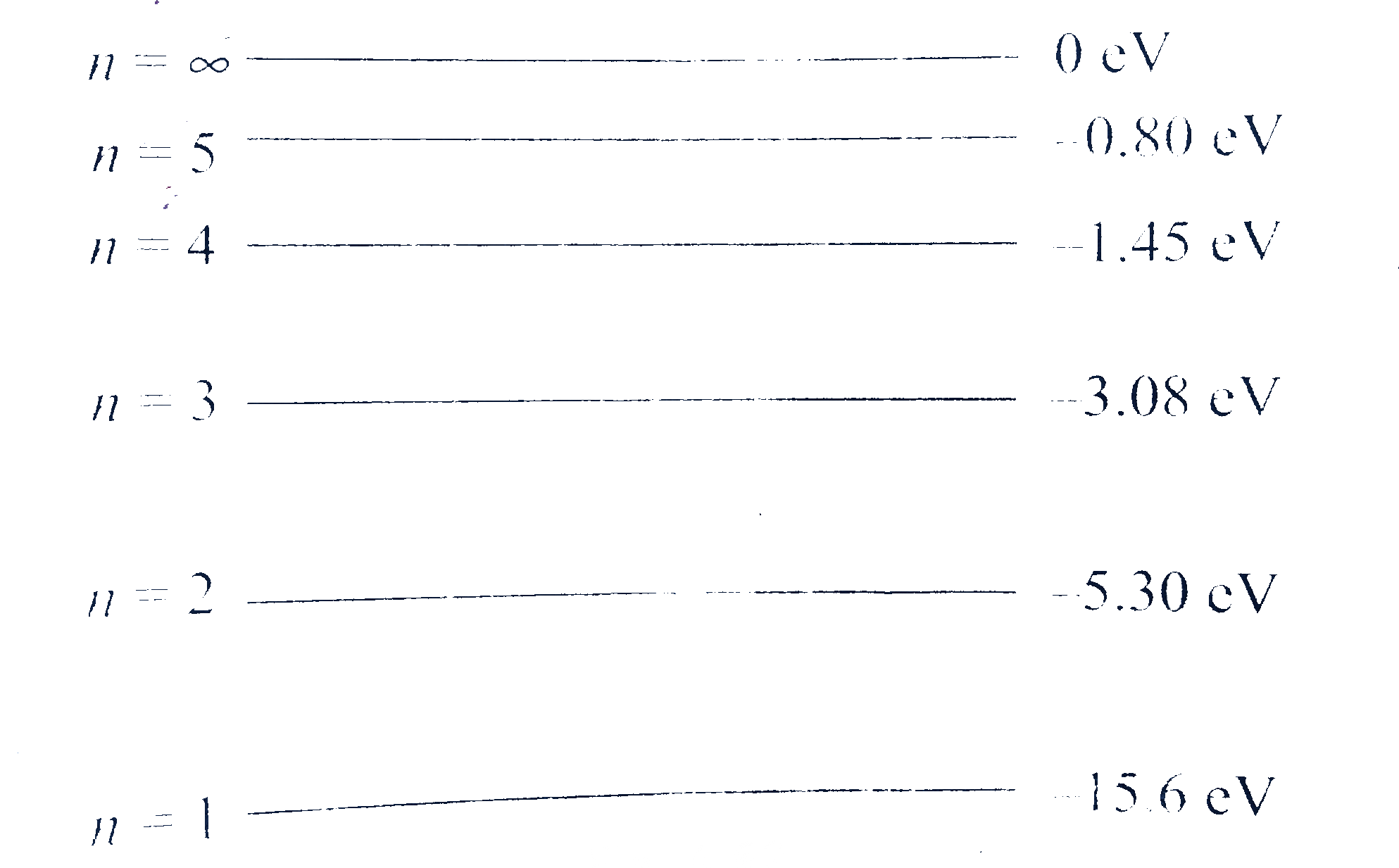
Find the wave number of the photon emitted for the transition n=3→n=1
View SolutionIf an electron having kinetic energy 2eV is accelerated through the potential difference of 2 volt. Then calculate the wavelength associated with the electron
View SolutionAn electron is excited to fourth energy level in an atom. It will
View SolutionFigure shown the electron energy level , referred to the ground state (the lowest possible energy) as zero , for five different isoleted atoms. Which atom can produce radiation of the shortest wavelength when atoms in the ground state are bombarded with electrons energy W?

View SolutionIf the energy in the first excited state in hydrogen atom is 23.8eV then the potential energy of a hydrogen atom in the ground state can be assumed to be
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
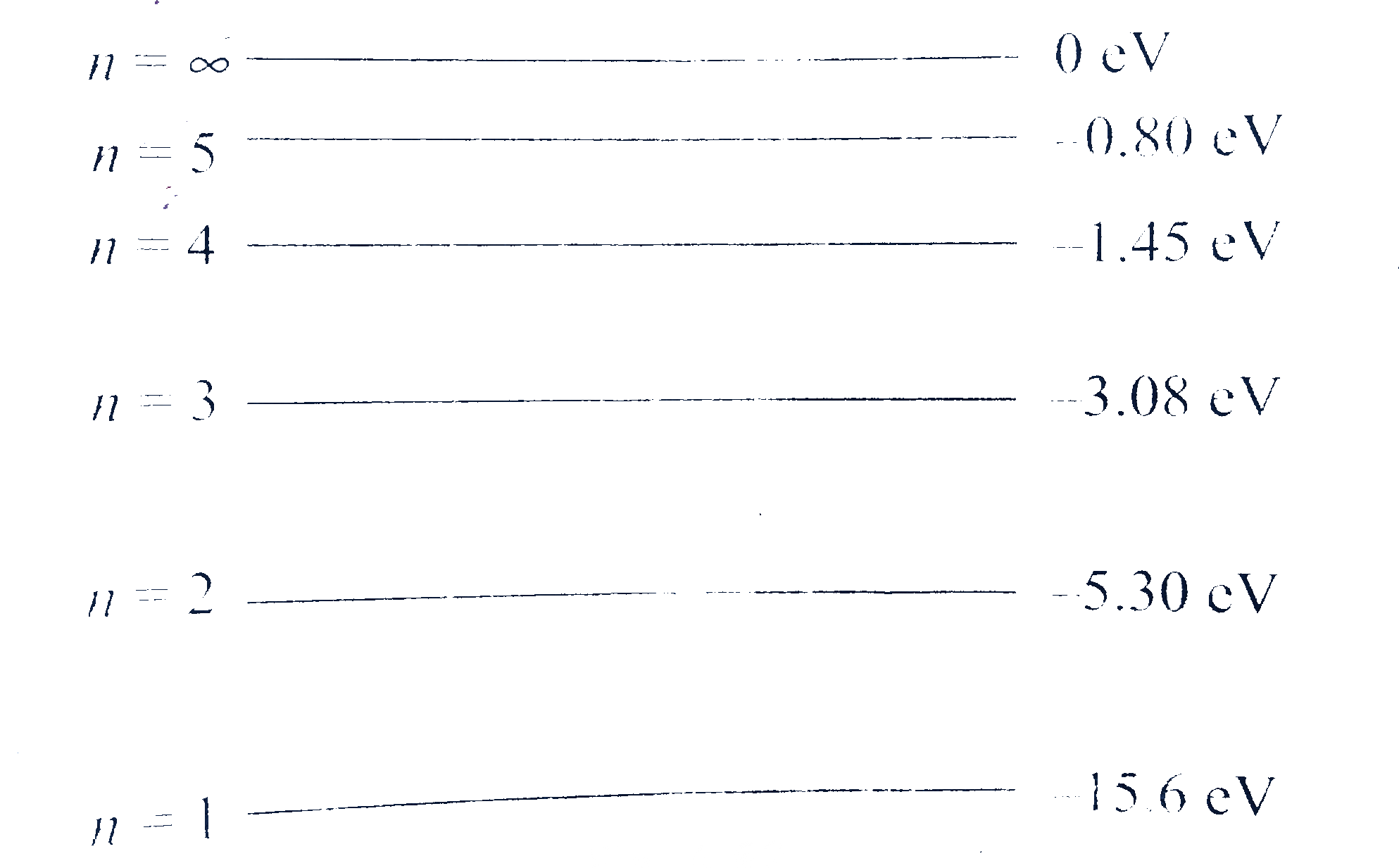
If an electron with initial kinetic energy 6eV is to interact with this hypothetical atom , what minimum energy will this electron carry after interaction?
View Solution
