Complete Solutions to Solved Examples of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| CENGAGE PHYSICS | Solved Examples |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Ultraviolet light of wavelength `800 A` and `700 A` when allowed to fall on hydrogen atoms in their ground states is found to liberate electrons with kinetic energies `1.8eV` and `4.0eV`, respectively. Find the value of Planck's constant.
View SolutionA single electron orbit around a stationary nucleus of charge `+ Ze` where Z is a constant and e is the magnitude of the electronic charge. It requires`47.2 eV` to excite the electron from the second bohr orbit to the third bohr orbit. Find
(i) The value of Z
(ii) The energy required by nucleus to excite the electron from the third to the fourth bohr orbit
(iii) The wavelength of the electronmagnetic radiation required to remove the electron from the first bohr orbit to inlinity
(iv) The energy potential energy potential energy and the angular momentum of the electron in the first bohr orbit
(v) The radius of the first bohr orbit (The ionization energy of hydrogen atom ` = 13.6 eV ` bohr radius `= 5.3 xx 10^(-11) matre` velocity of light `= 3 xx 10^(8) m//sec` planks 's constant ` = 6.6 xx 10^(-34)` jules - sec )
View SolutionThe ionization energy of a hydrogen like bohr atom is `4` Rydbergs (i) What is the wavelength of the radiation emitted when the electron jumps from the first excited state to the ground state ?(ii) what is the radius of the orbit for this atom ?
View Solution(a)Find the wavelength of the radiation required to excited the electron is `Li^(++)` from the first to the third Bohr orbit (b) How many spectral lines are obseved in the emission spactrum of the above excited system?
View SolutionThe energy of an electron in an excited hydrogen atom is `- 3.4 e V`. Calculate the angular momentum . Given : Rydbrg's `R = 1.09737 xx 10^(-7) m^(-1)`. Plank's constant `h = 6.626176 xx 10^(-34) J - s`, speed of light`c = 3 xx 10^(8) m s^(-1).
View SolutionLight of wavlength of `2000 A` falls on an aluminimum surface. In aluminium, `4.2eV` are required to remove an electron from its surface. What is the kinetic energy, in electron volt, of (a) the fastest, and (b) the slowest emitted photo-electrons. © What is the stopping potential? (Planck's constant `h=6.6xx10^(-34)J s`, and speed of light `c=3xx10^(8)ms^(-1))`
View SolutionFind the frequency of light which ejects electrons from a metal surface. Fully stopped by a retarding potential of `3 V`, the photoelectric effect begins in this metal at a frequency of `6xx10^(14)Hz`. Find the work function for this metal. (Given `h=6.63xx10^(-34)Js`).
View SolutionA 40 W ultraviolet light source of wavelength `2480 A`. Illuminates a magnesium (mg) surface placed 2 m away. Determine the number of photons emitted from the surface per second and the number incident on unit area of Mg surface per second . The photoelectric work function for Mg is `3.68eV`. Calculate the kinetic energy of the fastest electrons ejected from the surface. Determine the maximum wavelength for which the photoelectric effects can be observed with Mg surface.
View SolutionHydrogen atom is ground state is excited by mean of monochromatic radiation of wavelength `975Å` How many different lines are possible in the resulting spectrum ? Calculate the longest wavelength for hydrogen atom as ionization energy is`13.6 eV`
View SolutionA gas of identical hydrogen-like atoms has some atoms in the lowest in lower (ground) energy level `A` and some atoms in a partical upper (excited) energy level `B` and there are no atoms in any other energy level.The atoms of the gas make transition to higher energy level by absorbing monochromatic light of photon energy `2.7 e V`.
Subsequenty , the atom emit radiation of only six different photon energies. Some of the emitted photons have energy `2.7 e V` some have energy more , and some have less than `2.7 e V`.
a Find the principal quantum number of the intially excited level `B`
b Find the ionization energy for the gas atoms.
c Find the maximum and the minimum energies of the emitted photons.
View SolutionThe wavelength of the characteristic X - ray `k_(alpha )` line emitted by a hydrogens like element is `0.32 lambda ` . The wavelength of the `K_(beta)` line emitted by the same element will be …..
View SolutionLight form a dicharge tube containing hydrogen atoms falls on the surface of a piece of sodium. The kinetic energy of the fastest photoelectrons emitted from sodium is 0.73 eV. The work function for sodium is 1.82 eV. Find (a) the energy of the photons causing the photoelectrons emission.
(b) the quantum numbers of the two levels involved in the emission of these photons.
(c ) the change in the angular momentum of the electron in the hydrogen atom, in the above transition, and
(d) the recoil speed of the emitting atom assuming it to be at rest before the transition. (lonization potential of hydrogen is 13.6 eV.)
View SolutionTwo hydrogen-like atoms `A` and `B` are of different masses and each atom contains equal numbers of protons and neutrons. The difference in the energies between the first Balmer lines emitted by `A and B` , is `5.667 e V`. When atom atoms `A and B` moving with the same velocity , strike a heavy target , they rebound with the same velocity in the process, atom `B` imparts twice the momentum to the target than that `A` imparts. Identify the atom `A and B`.
View Solutiona. A stopping potential of `0.82V` is required to stop the emission of photoelectrons from the surface of a metal by light of eavelength `4000 A`. For light of wavelength `3000 A`, the stopping potential is `1.85V`. Find the value of Planck's constant. [1 electrons volt (eV)`=1.6xx10^(-19)J]`
b. At stopping potential, if the wavelength of the incident light is kept fixed at `4000 A`, but the intensity of light increases two times, will photoelectric current be botained ? Give reasons for your answer.
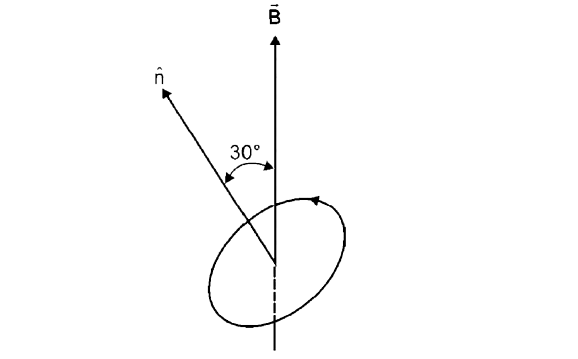
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius `R`.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction `vec(B)` such that the plane - normal of the electron - orbit makes an angle of ` 30^(@)` with the magnetic induction . Find the torque experienced by the orbiting electron.
View SolutionThe radiation emitted when an electron jumps from `n=3` to `n=2` orbit of hydrogen atom falls on a metal to produce photoelectrons. The electrons emitted from the metal surface with maximum kinetic energy are made to move perpendicular to a magnetic field of `(1)/(320)` T is a radius of `10^-3m`. Find:
A. the kinetic energy of the electrons,
B. work function of metal, and
C. wavelength of radiation.
(Planck's constant `h=6.62xx10^-32J-s`)
View SolutionAn electron, in a hydrogen like atom , is in excited state. It has a total energy of -3.4 eV, find the de-Broglie wavelength of the electron.
View SolutionAssume that the de-Broglie were associated with an electron can form a standing wave between the atoms arranged in a one dimensional array with nodes at each of the atomic sites. It is found that one such standing wave is formed if the distance d between the atoms of the array is `2 Å`. A similar standing wave is again formed if d is increased to `2.5 Å` but not for any intermediate value of d. Find the energy of the electron in eV and the least value of d for which the standing wave of the type described above can form.
View SolutionA gas of hydrogen like ions is prepared in such a way that ions are only in the ground state and the first excited state. A monochromatic light of wavelength 1216 Å is absorbed by the ions. The ions are lifted to higher excited states and emit radiations of six wavelengths. Find the principal quantum number of the final excited state.
View SolutionPhotoelectrons are emitted when `400 nm` radiation is incident on a surface of work - function 1.9 eV. These photoelectrons pass through a region containing `alpha`-particles. A maximum energy electron combines with an `alpha` -particle to from a `He^+` ion, emitting a single photon in this process. `He^+` ions thus formed are in their fourth excited state. Find the energies in eV of the photons lying in the 2 to 4 eV range, that are likely to be emitted during and after the combination. `[Take, h = 4.14xx10^(-15) eV -s]`
View SolutionWhen a beam of 10.6 eV photons of intensity 2.0 `W//m^(2)` falls on a platinum surface of area `1.0xx10^(-4)m^(2)` and photons eject photoelectrons. Find the number of photoelectrons emitted per second
View SolutionAn electron in hydrogen-like atom makes a transition from nth orbit or emits radiation corresponding to Lyman series. If de Broglie wavelength of electron in nth orbit is equal to the wavelength of rediation emitted , find the value of `n` . The atomic number of atomis `11`.
View SolutionAn X-ray tube operated at `40 k V` emits a continous X-ray spectrum with a short wavelength limit `lambda_(min) = 0.310 Å`. Calculate Plank's constant.
View Solution
Solved Examples questions and complete solutions for chapter ATOMIC PHYSICS of CENGAGE PHYSICS (ENGLISH) of Class 12