Complete Solutions to single correct Answer Type of chapter SOURCES OF MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SOURCES OF MAGNETIC FIELD |
| CENGAGE PHYSICS DPP | single correct Answer Type |
| Number Of Questions | 37 |
| Academic Year | 2023-24 |
Two very thin metallic wires placed X and Y-axis carry equal currents as shown here. AB and CD are lines at `45^(@)` with the axes with origin of axes at O. The magnetic field with be zero on the line

View SolutionTwo parallel beams of protons and electrons, carrying equal currents are fixed at a separation d. The protons and electrons move in opposite directions. P is a point on a line joining the beams , at a distacne x from any one beam. The magnetic field at P is B . If B is plotted against x, which of the following best represents the resulting curve
View SolutionA straight section PQ of a circuit lies along the x-axis from `x=-(a)/(2)` to `x=(a)/(2)` and carries a steady current i. The magnetic field due to the section PQ at a point x =+a will be
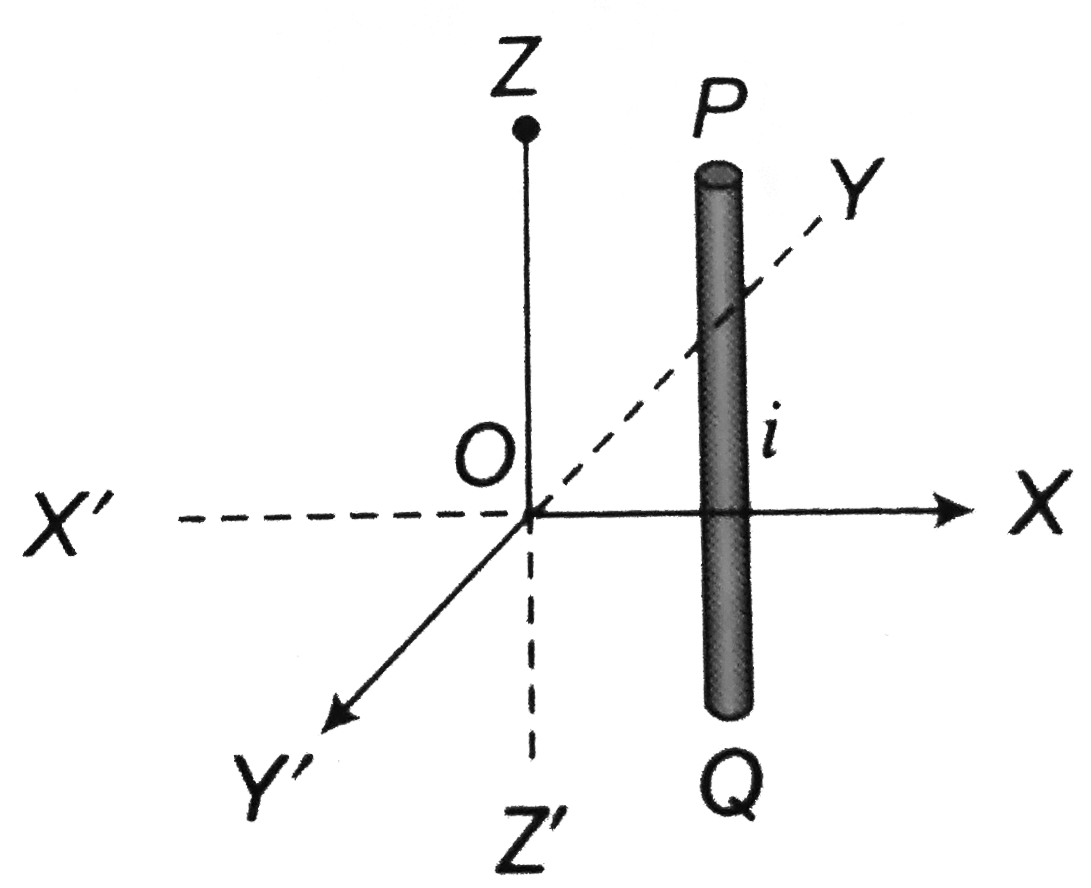
View SolutionA vertical wire kept in `Z-X` plane carries a current from `Q` to `P` (see figure). The magnetic field due to current will have the direction at the origin `O` along
View SolutionA long straight wire carrying current of `30 A` is placed in an external unifrom magnetic field of induction `4xx10^(4) T`. The magnetic field is acting parallel to the direction of current. The maggnetic of the resultant magnetic inuduction in tesla at a point `2.0 cm` away form the wire is
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant `L/4` from its centre will be-
View SolutionTwo parallel long wires carry currents `i_(1) "and" i_(2)` with `i_(1) gt i_(2)`.When the currents are in the same direction then the magnetic field midway between the wires is `10 mu T.` when the direction of `i_(2)` is reversed ,then it becomes `40 mu T.` then ratio of `i_(1)//i_(2)` is
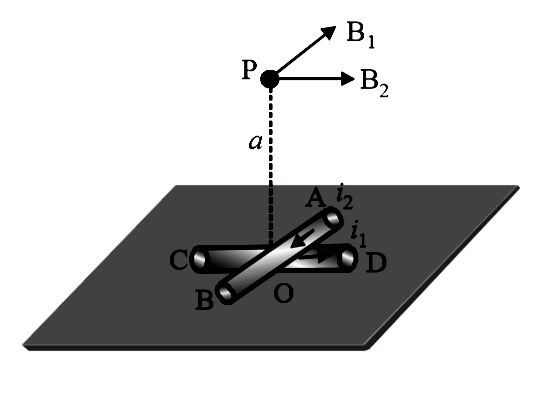
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current `i_(1)` and `i_(2)`. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
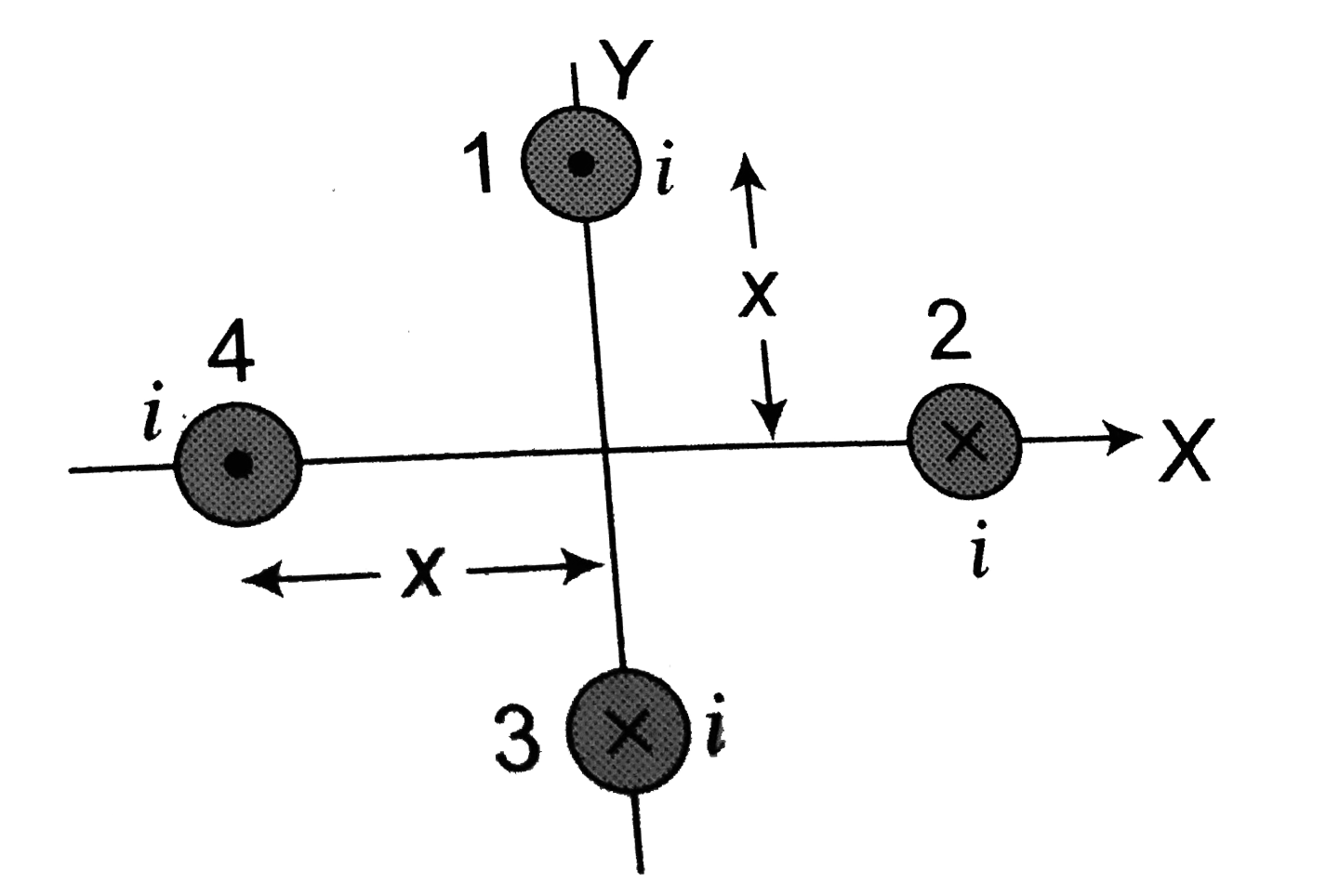
View SolutionWhat will be the resulatant field at the origin due to the four indinite length wires if each wire produces magnetic field `B` at origin ?
View SolutionAB and CD are long straight conductor, distance d apart, carrying a current l. The magnetic field at the midpoint of BC is

View SolutionFigure shows a square loop ABCD with edge length `a`. The resistance of the wire ABC is `r` and that of ADC is `2r`. Find the magnetic field B at the centre of the loop assuming uniform wires. `

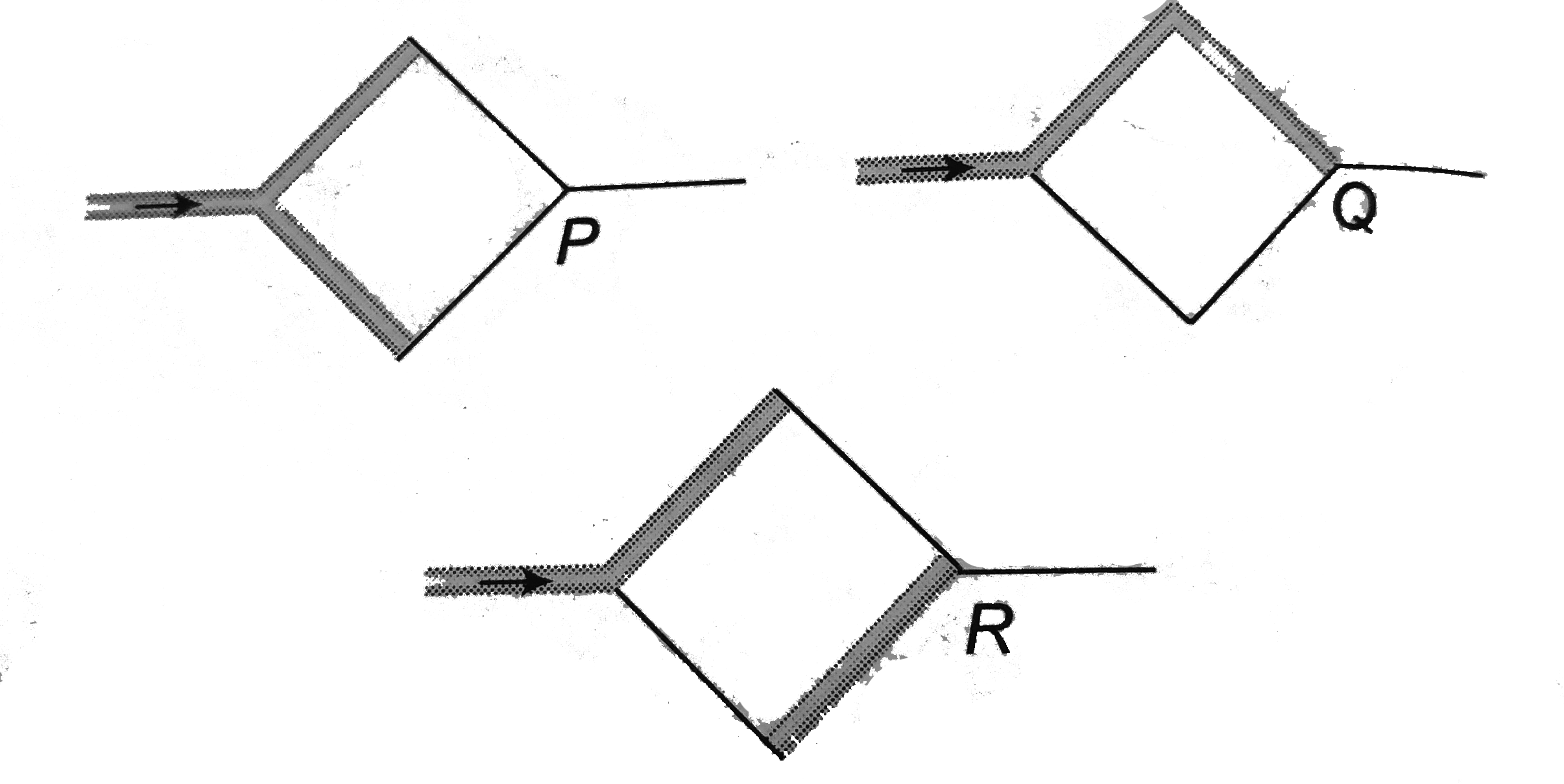
View SolutionTwo thick wires and two thin wires, all of the same materais and same length from a square in the three differenct ways, `P,Q` and `R` as shwon in figure with current connection shown, the magneitc feidl at the centre of the square is zero in cases.
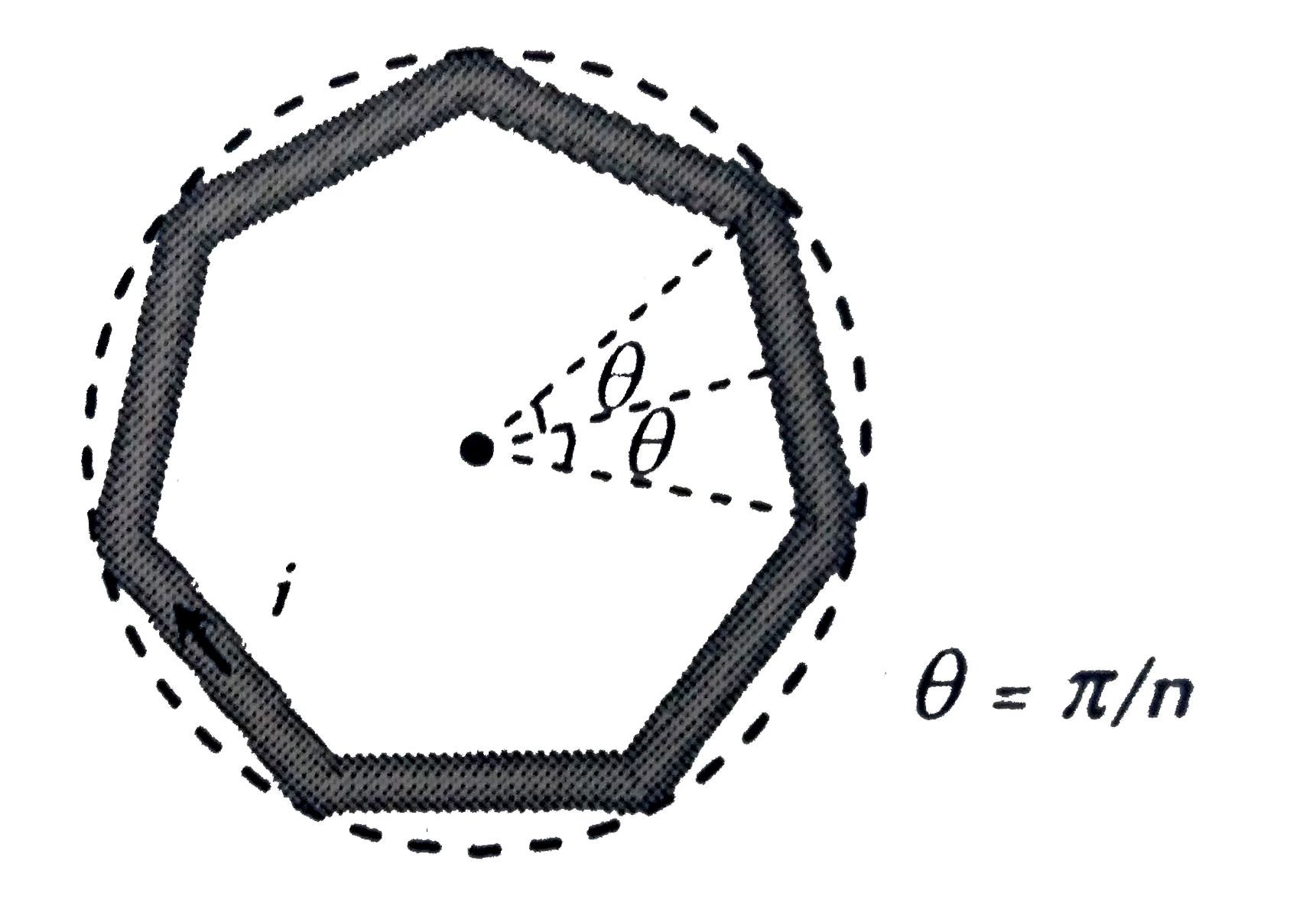
View SolutionIn the following figure a wire bent in the form of a regular polygon of `n` sides is inscribed in a circle of radius `a`. Net magnetic field at centre will be
View SolutionA coil carrying a heavy current and having large number of turns mounted in a N-S vertical plane and current flow in clockwise direction. A small magnetic needle at its center will have its north pole in
View SolutionAn electron is revolving round a proton, producing a magnetic field of `16 weber//m^(2)` in a circular orbit of radius `1 Å. Its angular velocity will be
View SolutionA thin wire of length `l` is carrying a constant current. The wire is bent to form a circular coil. If radius of the coil, thus formed, is equal to R and number of turns in it is equal to `n`, then which of the following graphs represent (s) variation of magnetic field induction (B) at centre of the coil
View SolutionA neutral point is obtained at the centre of a vertical circular coil carrying current. The angle between the plane of the coil and the magnetic meridian is
View SolutionTwo concentric coplanar circular loops of radii `r_(1)` and `r_(2)` carry currents of respectively `i_(1)` and `i_(2)` in opposite direction (one clockwise and the other anticlockwise). The magnetic induction at the centre of the loops is half that due to `i_(1)` alone at the centre. if `r_(2)=2r_(1)`. the value of `i_(2)//i_(1)` is
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View SolutionA current `i` ampere flows in a circular arc of wire whose radius is `R`, which subtend an angle `3pi//2` radian at its centre. The magnetic induction `B` at the centre is

View SolutionIn the figure shown there are two semicircles of radii `r_(1)` and `r_(2)` in which a current `i` is flowing. The magnetic induction at the centre `O` will be

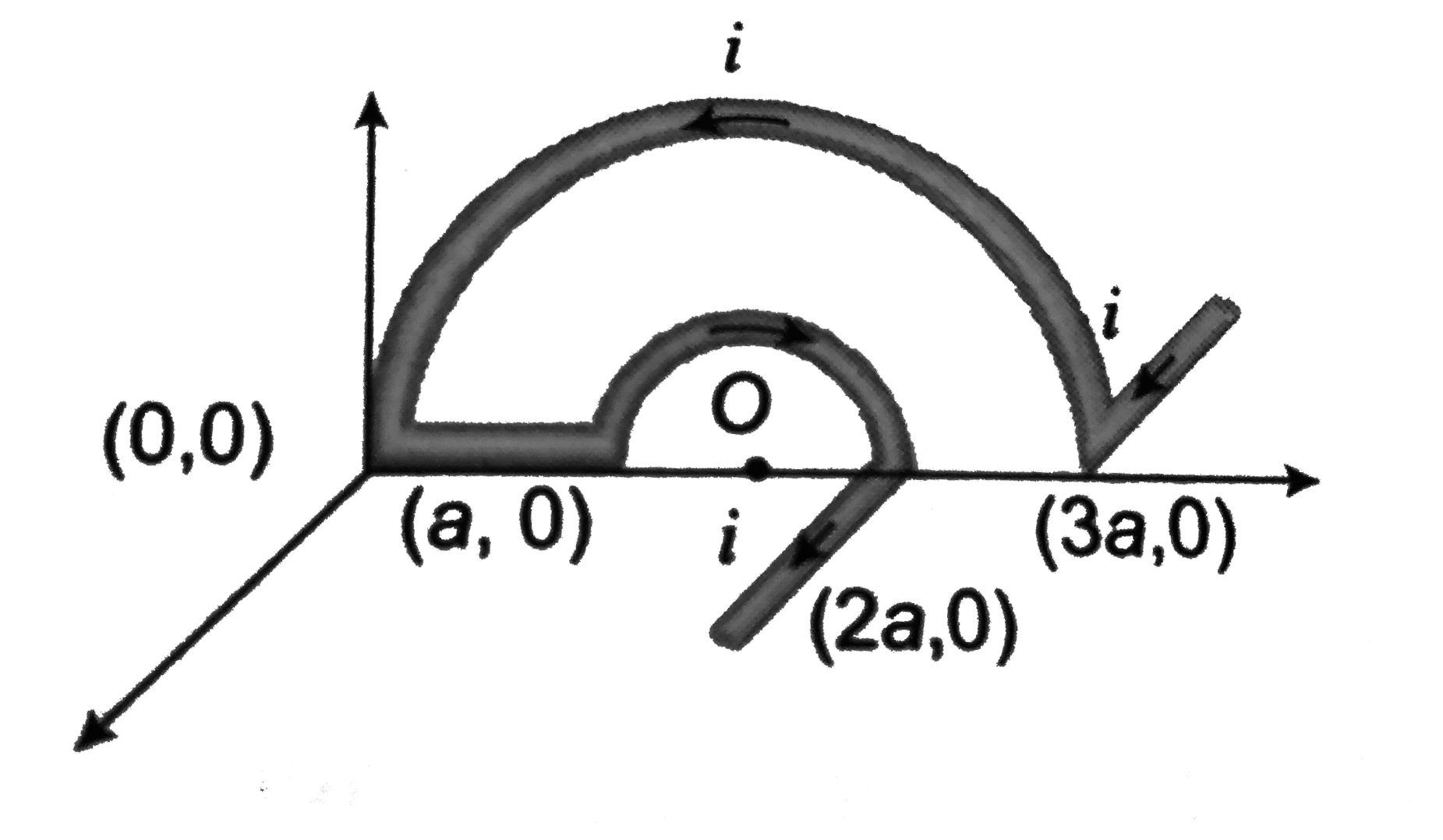
View SolutionFind magneitc field at O

View SolutionAn infinitely long straight conduction is bent into the shape as shown in the figure . It carries a current of I ampere and the radius of the circular loop is r metre. Then the magnetic induction at its centre will be

View SolutionA part of a long wire carrying a current `i` is bent into a circle of radius `r` as shown in figure. The net magnetic field at the centre `O` of the circular loop is

View SolutionIn the figure, what is the magnetic field at the point `O`?

View SolutionA circular current carrying coil has a radius R. The distance from the centre of the coil on the axis where the magnetic induction will be `(1)/(8)` th to its value at the centre of the coil, is
View SolutionTwo circular coils X and Y, having equal number of turns and carrying currents in the same sense, subtend same solid angle at point O. If the smaller coil X is midway between O and Y and if we represent the magnetic induction due to bigger coil Y at O as `B_y` and the due to smaller coil X at O as `B_x`,then find the ratio `B_x//B_y`.

View SolutionThe field normal to the plane of a wire of `n` turns and radis `r` which carriers `i` is measured on the axis of the coil at a small distance `h` from the centre of the coil. This is smaller than the field at the centre by the fraction.
View SolutionThe magnetic field at the centre of a circular coil of radius r is `pi` time that due to a long straight wire at a distance r from it for equal currents. The following figure show three cases. In all cases the circular part has radius r and straight ones are infinitely long. For same current, the B field at the centre P in cases 1, 2, 3, has the ratio

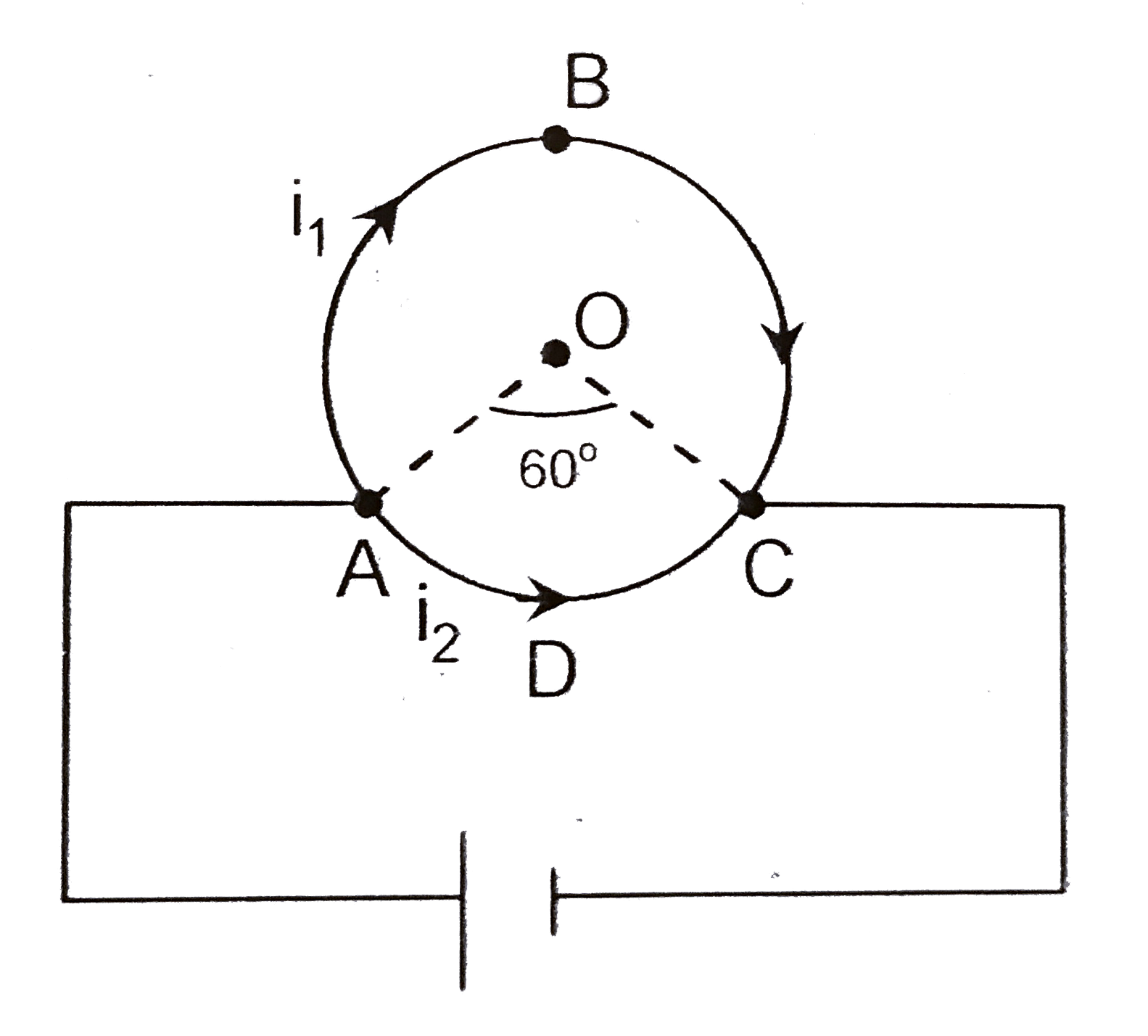
View SolutionA cell is connected between the point A and C of a circular conductor ABCD of centre `O, /_AOC = 60^(@)`. If `B_(1_` and `B_(2)` are the magnitude of magnetic fields at O due to the currents in ABC and ADC respectively, the ratio of `B_(1)//B_(2)` is.
View SolutionIn the given figure net magnetic at `O` will be
View Solutionthe unit vector `hat(i),hat(j)` and `hat(k)` are as shown below. What will be the magnetic field at O in the following figure ?

View SolutionA staright wire of length `(pi^(2))` meter is carrying a current of `2A` and the magnetic field due to it is measured at a point distant `1 cm` from it. If the wire is to be bent into a circles and is to carry the same current as before, the ratio of the magnetic field at its centre to that obtained in the first case would be
View SolutionFor the current carrying wire, show that the magnetic field at P is

View Solution`L` is a circular ring made of a uniform wire, currents enters and leaves the ring through straight conductors which, if produces, would have passed through the centre `C` of ring. The magnetic field at `C`
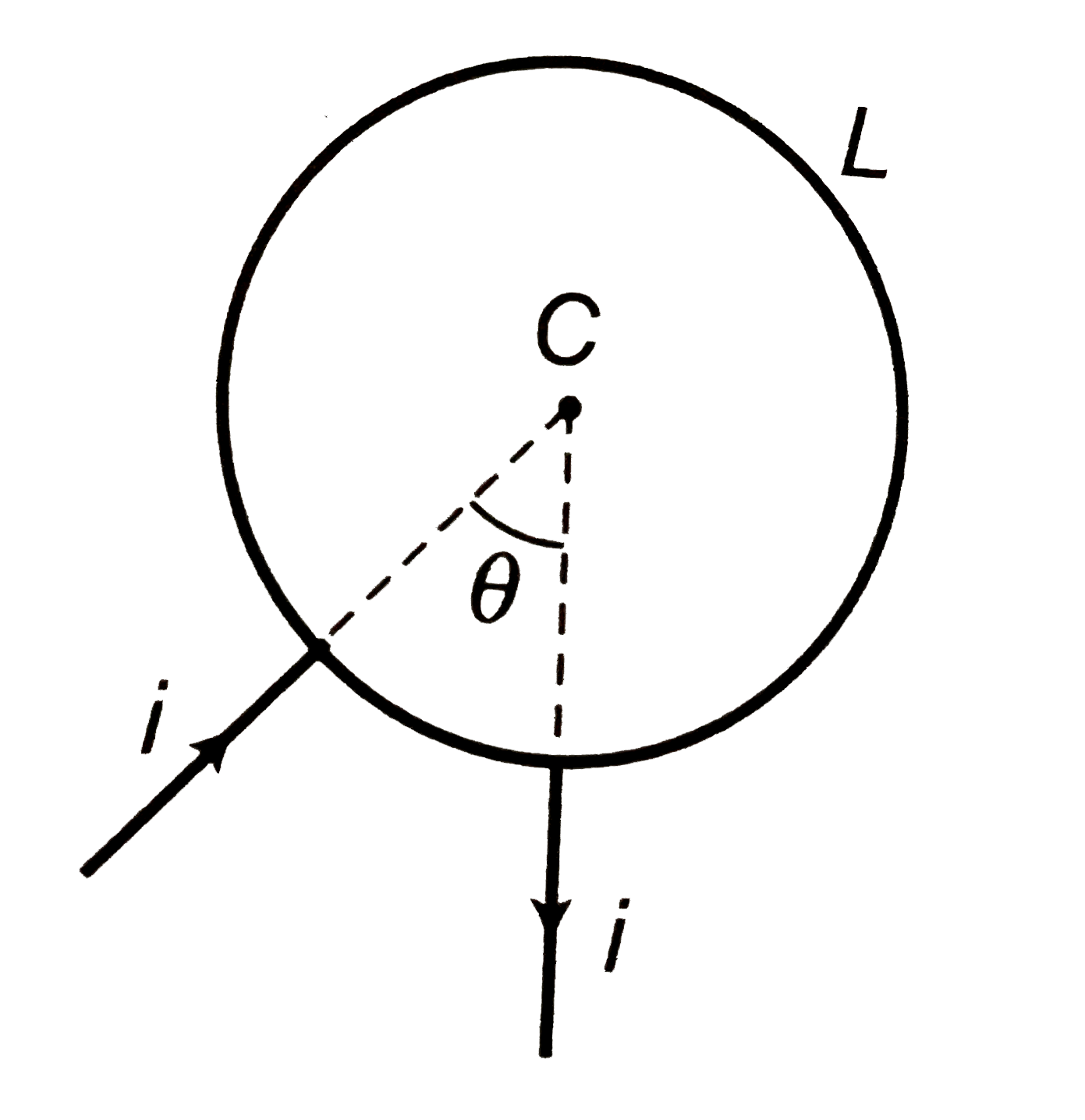
(i) due to the straight conductors is zero
(ii) due to the loop is zero
(iii) due to the loop is proportional to `theta`
(iv) due to loop is proportional to `(pi-theta)`
View SolutionTwo circular coils A and B with their centres lying on the same axis have differents in the same sence. The coil B lies exacity midway between coil A and the point P. The magnetic field at point P due to coils A and B is `B_(1)` and `B_(2)` respectively.
View SolutionFigure shows a long wire bent at the middle to from a right angle

View Solution
single correct Answer Type questions and complete solutions for chapter SOURCES OF MAGNETIC FIELD of CENGAGE PHYSICS (HINGLISH) of Class 12
All Exercises from CENGAGE PHYSICS DPP Class 12 PHYSICS SOURCES OF MAGNETIC FIELD
- Archives (fill In The Blanks)
- Archives (integer)
- Archives (linked Comprehension)
- Archives (multiple Correct )
- Archives (single Correct Anser)
- Concept Exercise 2.1
- Concept Exercise 2.2
- Exercise (assertion-reasioning )
- Exercise (integer)
- Exercise (linked Comprehension)
- Exercise (multiple Currect )
- Exercise (single Correct )
- Exercise (subjective )
- Illustration
- single correct Ansewer type
- single correct Answer Type
- Solved Example
- Subjective type