Complete Solutions to Illustration of chapter SOURCES OF MAGNETIC FIELD of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | SOURCES OF MAGNETIC FIELD |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
A point chanrge of magnitude `q=4.5nC` is moving with speed `v=3.6xx10^7ms^-1` parallel to the x-axis along the line `y=3m`. Find the magnetic field at the origin produced by this charge when the charge is at the point `x=-4 m`, `y=3m`, as shown in Fig.

View SolutionA long straight wire carrying current `i=10A` lies along y-axis. Find the magnetic field at P(3cm, 2cm,4cm).

View SolutionTwo long straight currents carrying wires having currents I and 2I lie along y-and z-axis, respectively, as shown in Fig. Find `vecB` at a point P(x,0).

View SolutionFind `vecB` at the origin due to the long wire carrying current I.

View SolutionA current I flows in a circuit shaped like an isosceles trapizium. The ratio of the bases is 2. The length of the smaller base is l. Calculate the megnetic field induction at point P located in the plane of the trapizium, but at a distance a from the midpoint of the smaller base,

View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionAn infinite carrying conductor is bent into three segment (1), (2) and (3) as shown in Fig. If it carries a current i, find the magnetic induction at the origin.
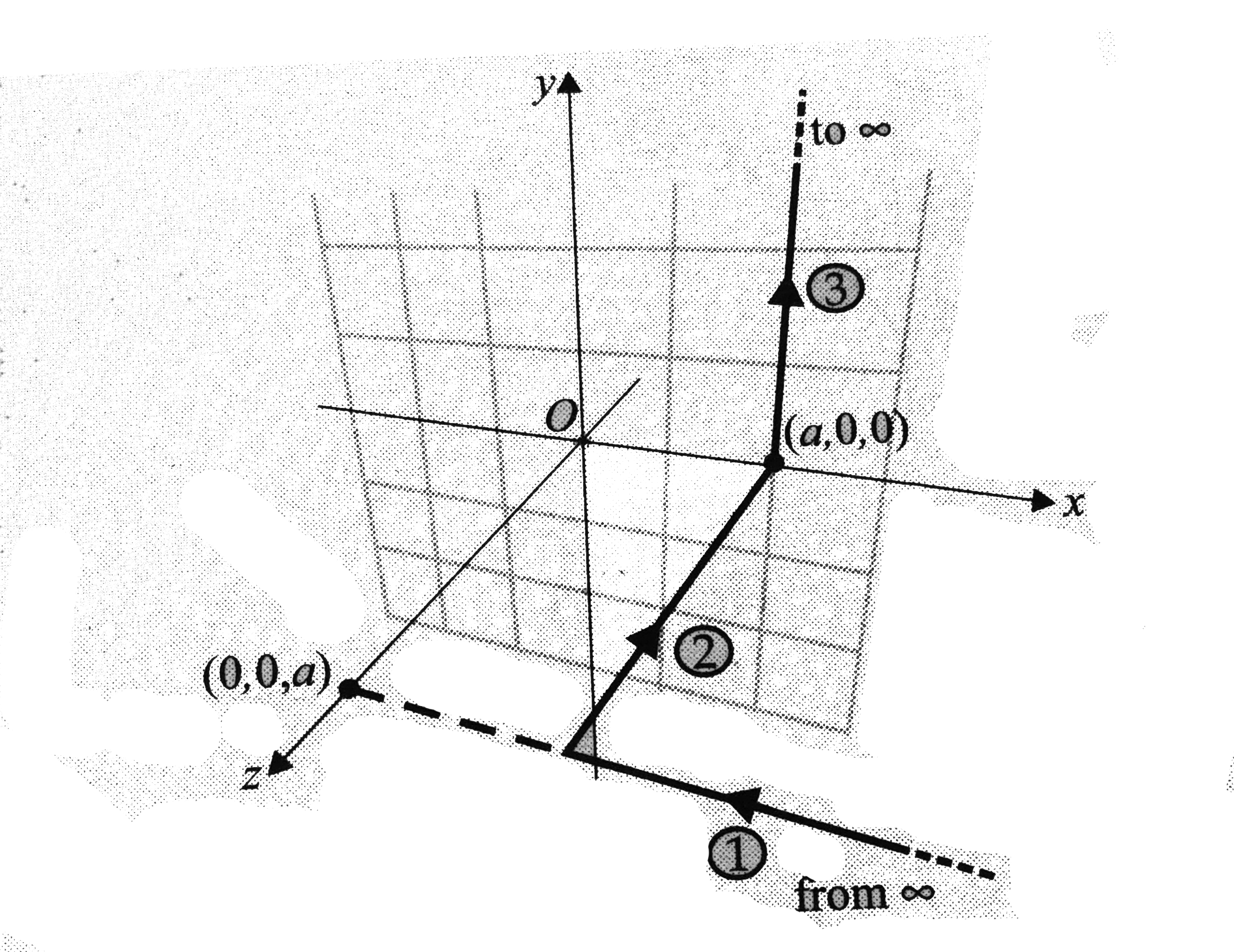
View SolutionFind the field at the origin O due to the current `i=2A`.
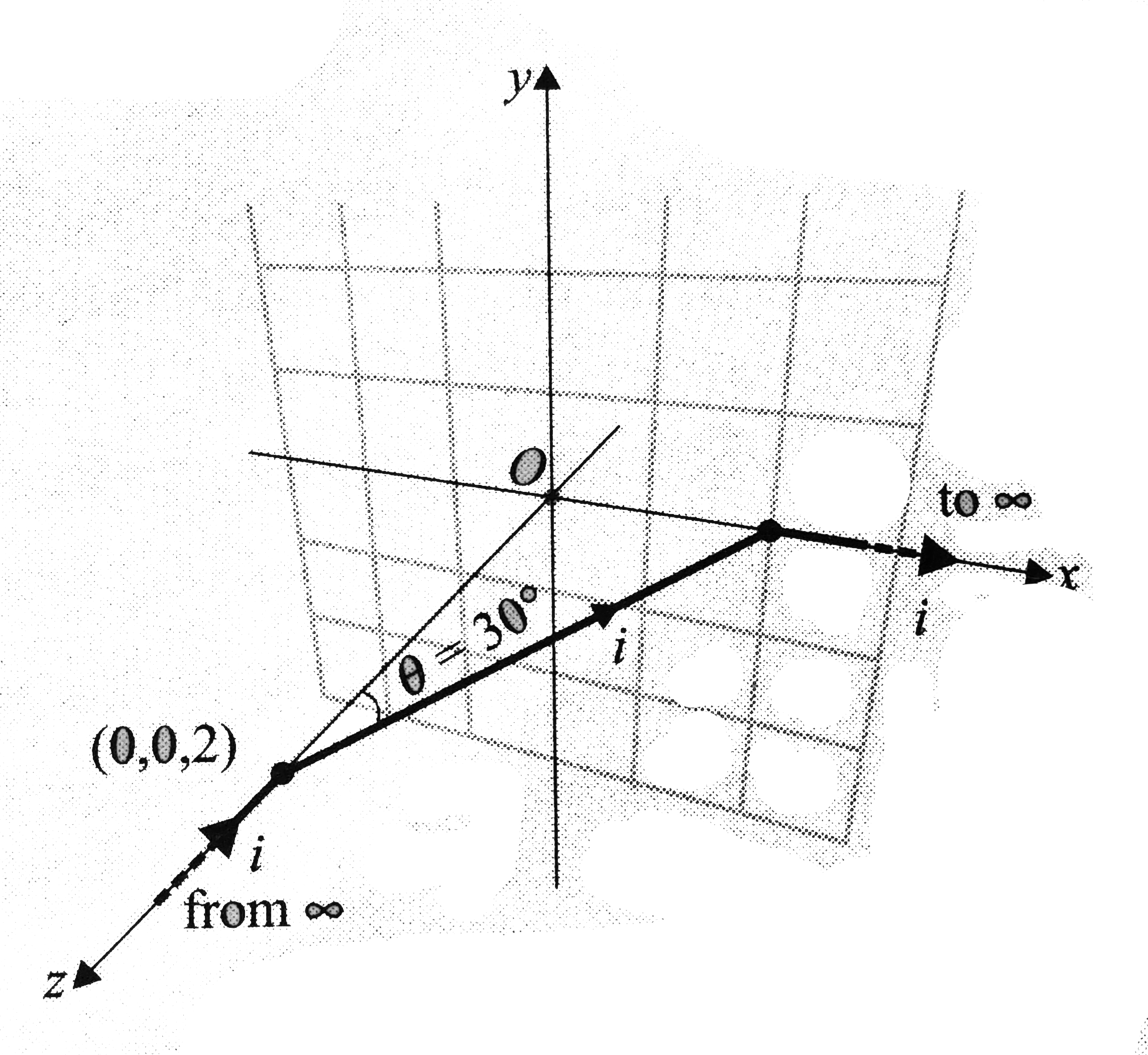
View SolutionA long straight wire, carrying current I, is bent at its midpoint to form an angle of `45^@`. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)

View SolutionTwo straight infinitely long and thin parallel wires are spaced 0.1m apart and carry a current of 10A each. Find the magnetic field at a point distance 0.1m from both wires in the two cases when the currents are in the (a) same and (b) opposite directions.
View SolutionIn Fig. Two long wires `W_1 and W_2`, each carrying current I, are placed parallel to each other and parallel to z-axis. The direction of current in `W_1`is outward and in `W_2` it is inward. Find `vecB` at p and Q.

View SolutionA square loop of wire, edge length a, carries a current i. Compute the magnitude of the magnetic field produced at a point on the axis of the loop at a distance x from the centre.
View SolutionCalculate the magnetic field at point O for the current-carrying wire segment shown in Fig. The wire consists of two straight portions and a circular arc of radius a, which subtends an angle `theta`.
View SolutionShown in Fig. is a conductor carrying current I. Find the magnetic field intensity at point O.
View SolutionA battary is connected between two points A and B on the circumference of a uniform conducting ring of radius r and resistance R as shown in Fig. One of the arcs AB of the ring subtends angle `theta` at the centre. Show that that the magnetic field at the centre of the coil is zero and independent `theta`.
View SolutionWhat is the magnitude of magnetic field at the centre O of loop of radius `sqrt2 m` made of uniform wire when a current of 1amp entres in the loop and taken out of it by two long wires as shown in the Fig.

View SolutionA thin insulated wire forms a plane spiral of `N=100` turns carrying a current `i=8mA`. The inner and outer radii are equal to `a=5 cm and b=10 cm`. Find the magnetic induction at the centre of the spiral

View SolutionA solenoid 60 cm long and of radius 4 cm has 3 layer of windings 300 turns each. A 2.3 cm long wire of mass 2.5g lies inside the solenoide near its centre normal to its axis, both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire?
View SolutionA solenoid of length `0.4 m` and diameter `0.6 m` consists of a single layer of `1000` turns of fine wire carrying a current of `5.0xx10^(-3)` ampere.The magnetic field strength on the axis at the middle is `pi/Nxx10^(-5)T`, then find value of `N`.
View SolutionTwo long parallel wires carry currents of equal magnitude but in opposite directions. These wires are suspended from rod PQ by four chords of same length L as shown in Fig The mass per unit length of the wires is `lambda`. Determine the value of `theta` assuming it to be small.

View SolutionTwo parallel horizontal conductors are suspended by two light vertical threads each 75 cm long. Each conductor has a mass of `40gm^-1`, and when there is no current they are 0.5 cm apart. Equal current in the two wires result in a separation of 1.5 cm. Find the values and directions of currents. Take `g=9.8ms^-2`.
View SolutionTwo infinetely long, parallel wires are lying on the ground at distance `a=1cm` apart as shown in Fig. A third wire, of length L=10m and mass 400g, carries a current of `I_1=100A` and is levitated above the first two wires, at a horizontal position midway between them. The infinitely long wires carry equal currents `I_1` in the same directions, but in the direction opposite that in the leviated wire. What current must the infinately long wires carry so that the three wires form an equilateral triangle?
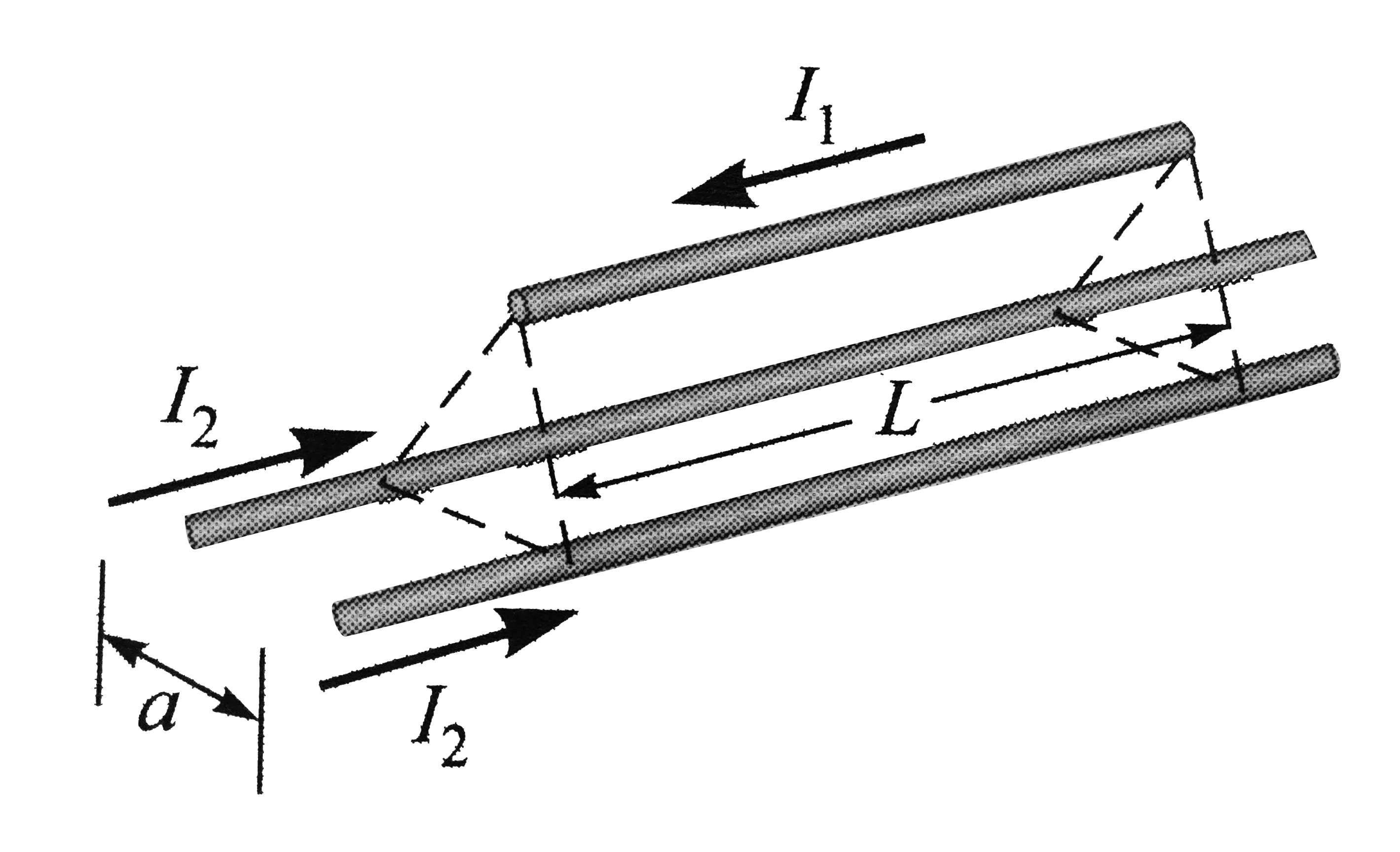

View SolutionWire 1 in Fig. is oriented along the y-axis and carries a steady current `I_1`. A rectangular loop located to right of the wire and in the x-y plane carries a current `I_1`. Find the magnetic force exerted by wire (1) on the top wire (1) on the top wire of length b in the loop, labeled "wire (2)" in the figure.
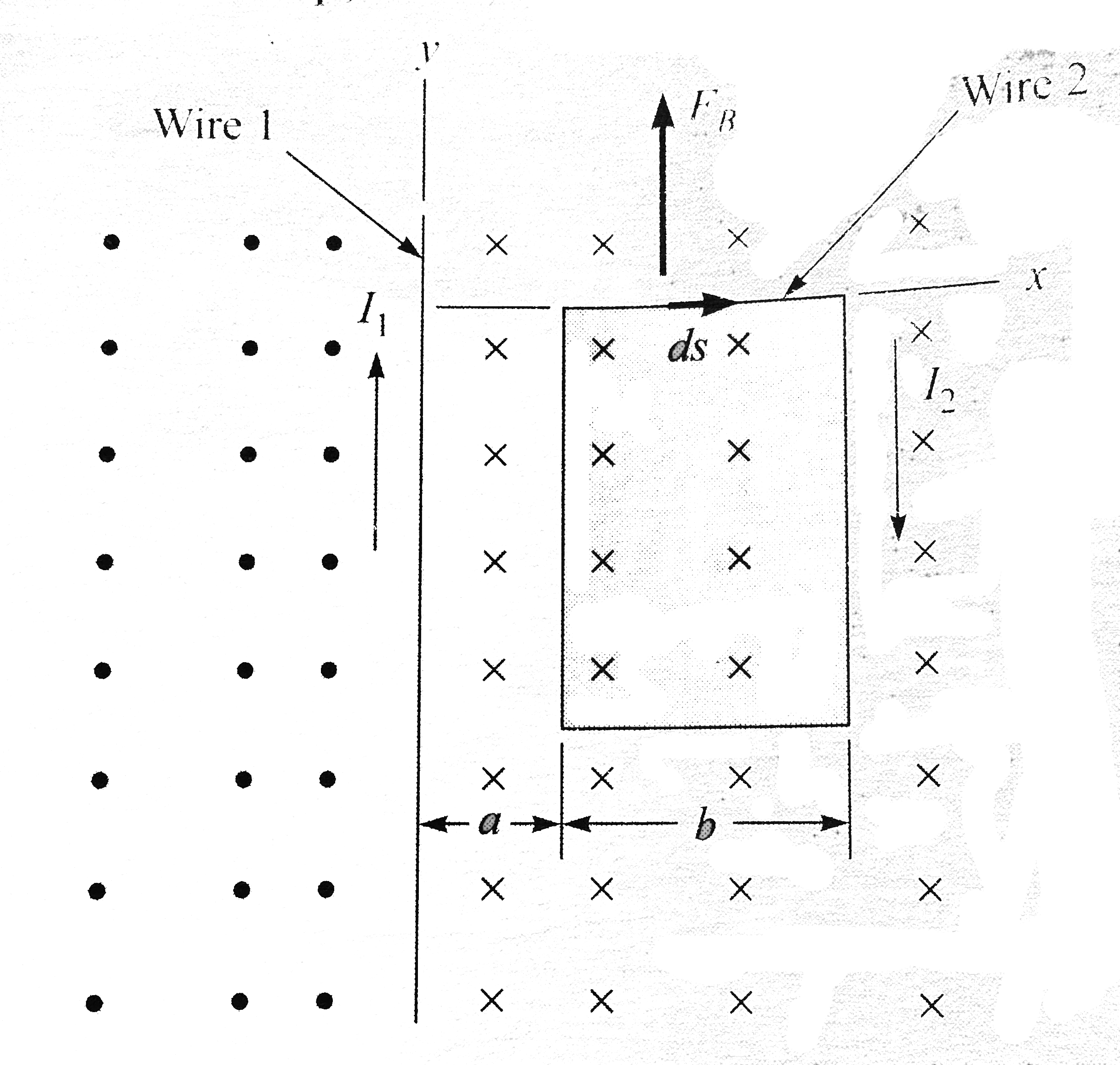
View SolutionFigure shows three current carrying conductors and three imaginary loops. Calculate the current enclosed by each of the loops.

View SolutionFigure shows two current carrying wires piercing the plane of an imaginary loop. One of the wires is normal to the plane of the loop while the other is at an angle. Calculate the net current enclosed.

View SolutionLet `B_P and B_Q` be the magnetic field produced by wire P and Q which are placed symmetrically in a rectangular loop ABCD. Current in wire P is directed I inward and in Q is 2I outward.
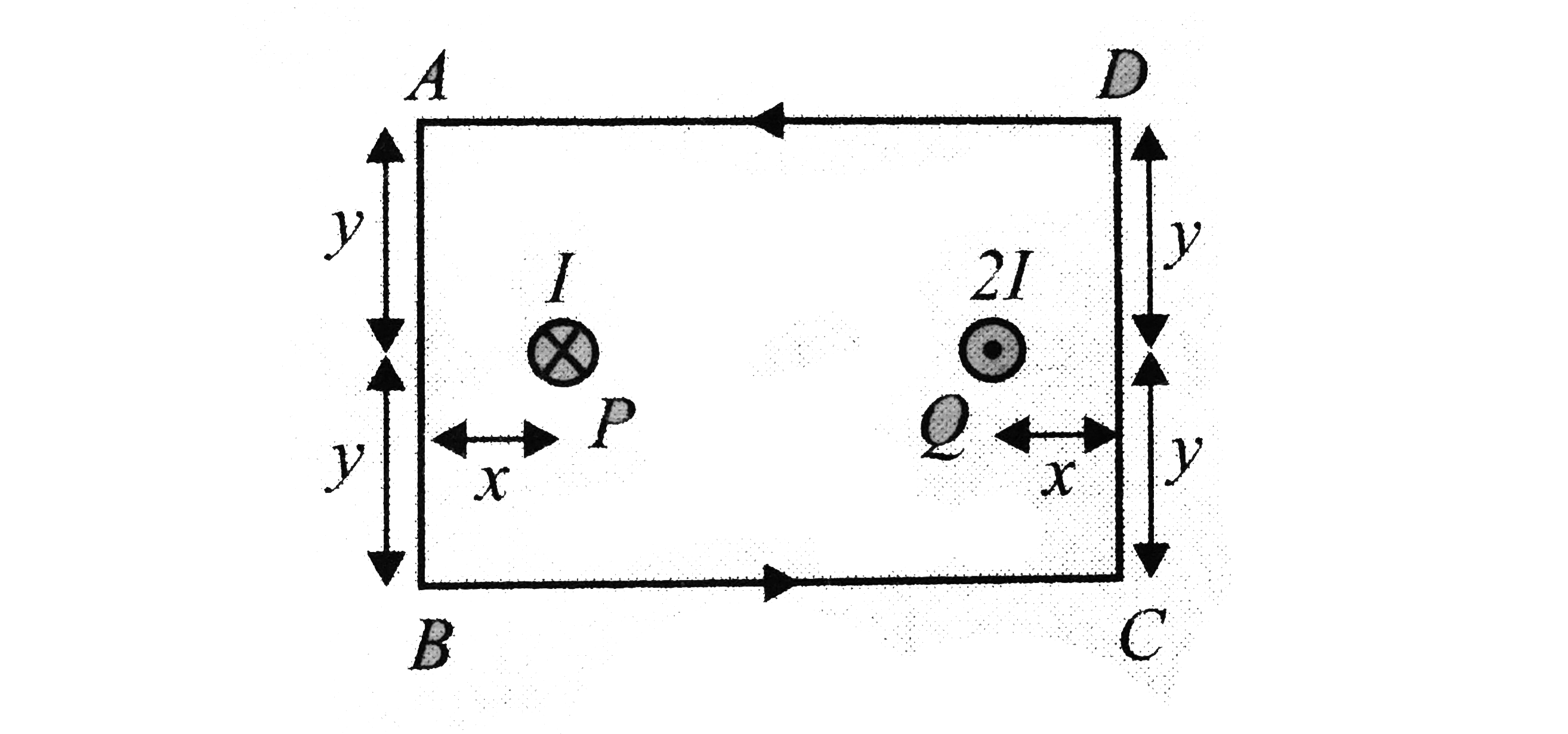
If `int_A^B vecB_Q.dvecl=2mu_0T-m`
`int_D^B vecB_P.dvecl=-2mu_0T-m`
`int_A^B vecB_P.dvecl=-mu_0T-m`
Then find I.
View SolutionConsider a coaxial cable which consists of an inner wire of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire carries an electric current `i_0` and the outer shell carries an equal current in opposite direction. Find the magnetic field at a distance x from the axis where (a) `xlta,` (b) `altxltb`, (c) `bltxltc` and (d)`xgtc`. Assume that the current density is uniform in the inner wire and also uniform in the outer shell.

View Solution
Illustration questions and complete solutions for chapter SOURCES OF MAGNETIC FIELD of CENGAGE PHYSICS (HINGLISH) of Class 12
All Exercises from CENGAGE PHYSICS Class 12 PHYSICS SOURCES OF MAGNETIC FIELD
- Archives (fill In The Blanks)
- Archives (integer)
- Archives (linked Comprehension)
- Archives (multiple Correct )
- Archives (single Correct Anser)
- Concept Exercise 2.1
- Concept Exercise 2.2
- Exercise (assertion-reasioning )
- Exercise (integer)
- Exercise (linked Comprehension)
- Exercise (multiple Currect )
- Exercise (single Correct )
- Exercise (subjective )
- Illustration
- single correct Ansewer type
- single correct Answer Type
- Solved Example
- Subjective type