Complete Solutions to Linked Comprehension of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| CENGAGE PHYSICS | Linked Comprehension |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
Hydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., `mvr = (nh//2 pi)`, where `m =` mass of the electron , `v =`velocity of the electron in the orbit , `r =`radius of the orbit , and `n = 1, 2, 3`.... When transition takes place from `Kth` orbit to `Jth` orbit, energy photon is emitted. If the wavelength of the emitted photon is `lambda`.
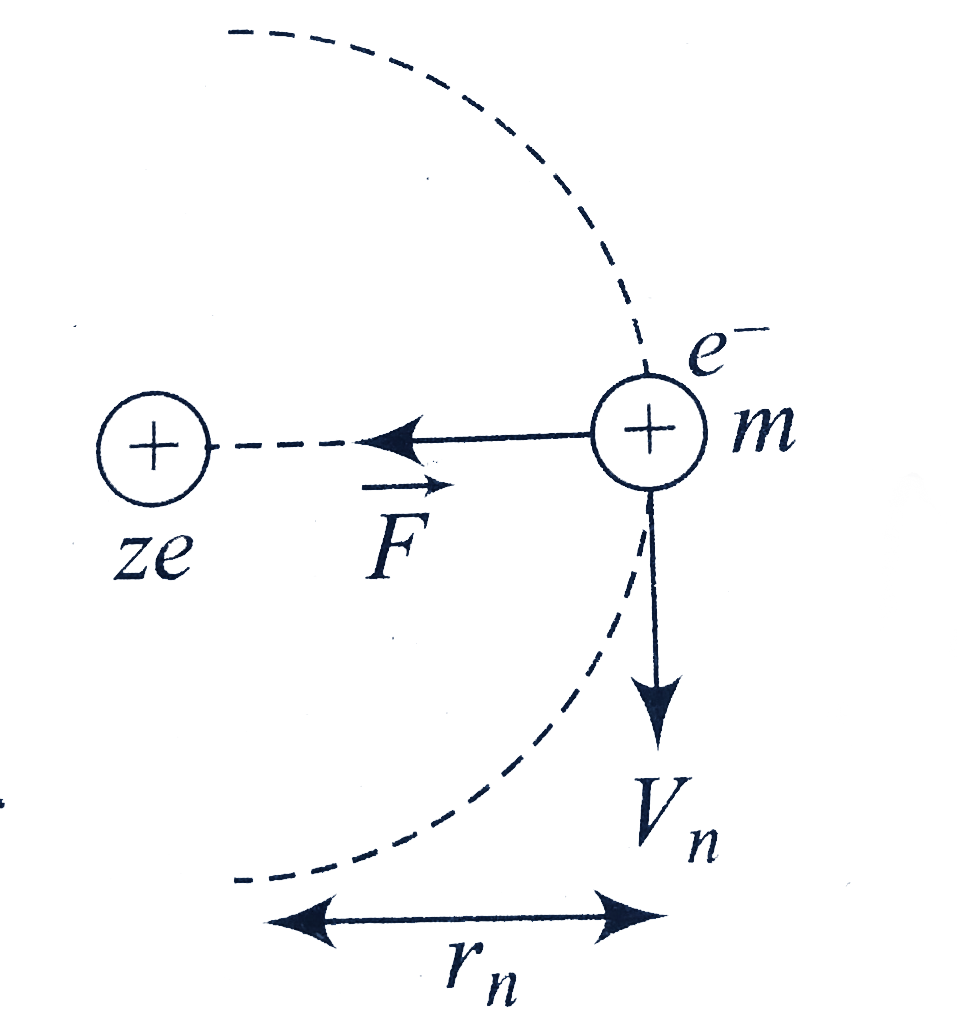
we find that `(1)/(lambda) = R [(1)/(J^(2)) - (1)/(K^(2))]`, where `R` is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was `P = 2n (h//2 pi)`. i.e., an even multipal of `(h//2 pi)`.
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is `v_(0)` when the hydrogen atom is in the ground state on the other planet should be
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., `mvr = (nh//2 pi)`, where `m =` mass of the electron , `v =`velocity of the electron in the orbit , `r =`radius of the orbit , and `n = 1, 2, 3`.... When transition takes place from `Kth` orbit to `Jth` orbit, energy photon is emitted. If the wavelength of the emitted photon is `lambda`.
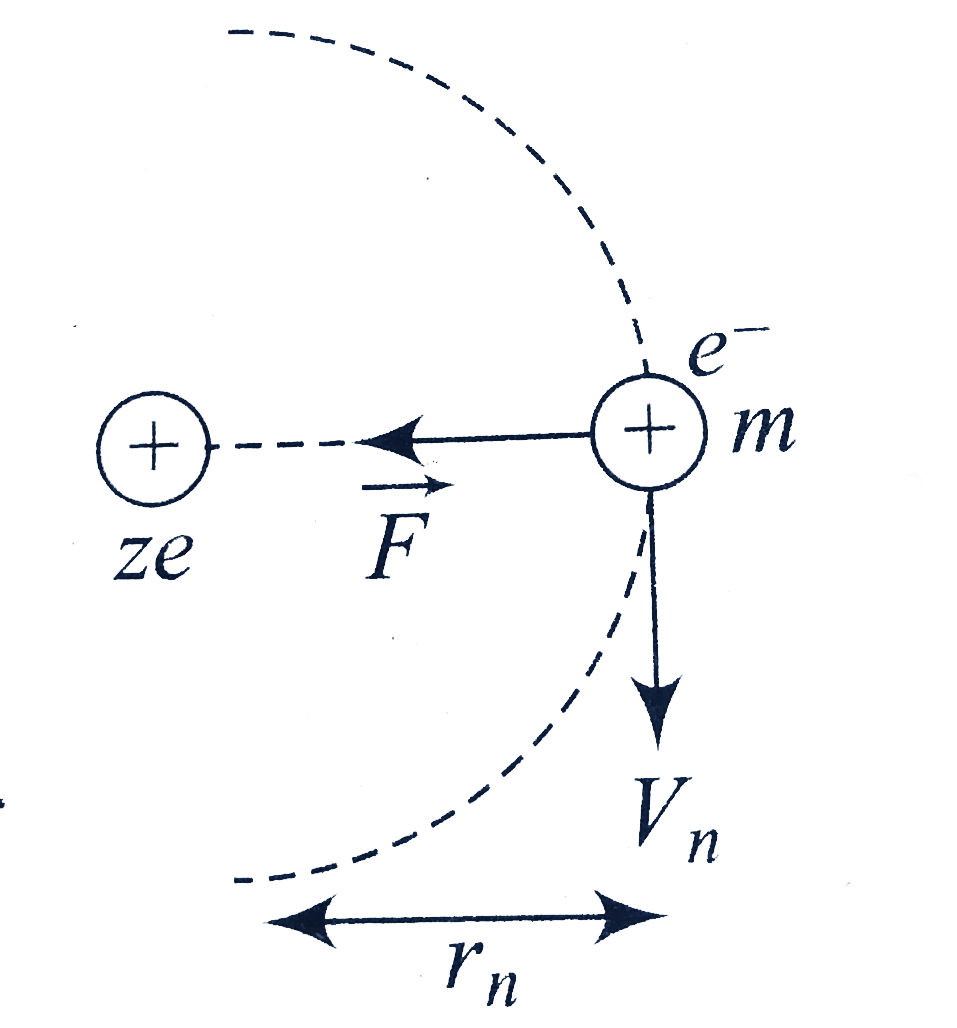
we find that `(1)/(lambda) = R [(1)/(J^(2)) - (1)/(K^(2))]`, where `R` is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was `P = 2n (h//2 pi)`. i.e., an even multipal of `(h//2 pi)`.
Answer the following questions regarding the other planet based on above passage:
In our world, the ionization potential energy of a hydrogen atom is `13.6 eV`. On the other planet, this ionization potential energy will be
View SolutionIn an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace `m_(e)` by what is known reduced mass is `m_(e)//2`.
The orbital radius of the first excited level of postronium atom is
View SolutionIn an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace `m_(e)` by what is known reduced mass is `m_(e)//2`.
If the Rydberg constant for hydrogen atom is `R` , then the Rydberg constant for positronium atom is
View SolutionIn an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace `m_(e)` by what is known reduced mass is `m_(e)//2`.
When system de-excites from its first excited state to ground state, the wavelngth of radiation is
View SolutionThe electrons in a `H`- atom kept at rest , jumps from the mth shell to the nth shell `(m gt n)`. Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
What principal is violated of inertia
View SolutionThe electrons in a `H`- atom kept at rest , jumps from the mth shell to the nth shell `(m gt n)`. Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
Calculate the angular velocity of the atom about the nucleus if `l` is the momentum of inertia
View SolutionThe electrons in a `H`- atom kept at rest , jumps from the mth shell to the nth shell `(m gt n)`. Suppose instead of emitting electromagnetic wave, the energy released is converted into kinetic energy of the atom. Assuming Bohr's model and conservation of angular momentum are valid. Now , answer the following questions:
If the above comprehension be true , ehat is not valid here?
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure

Find the ionization potential of the atom.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure

Find the short wavelength limit of the series terminating at `n = 2`.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
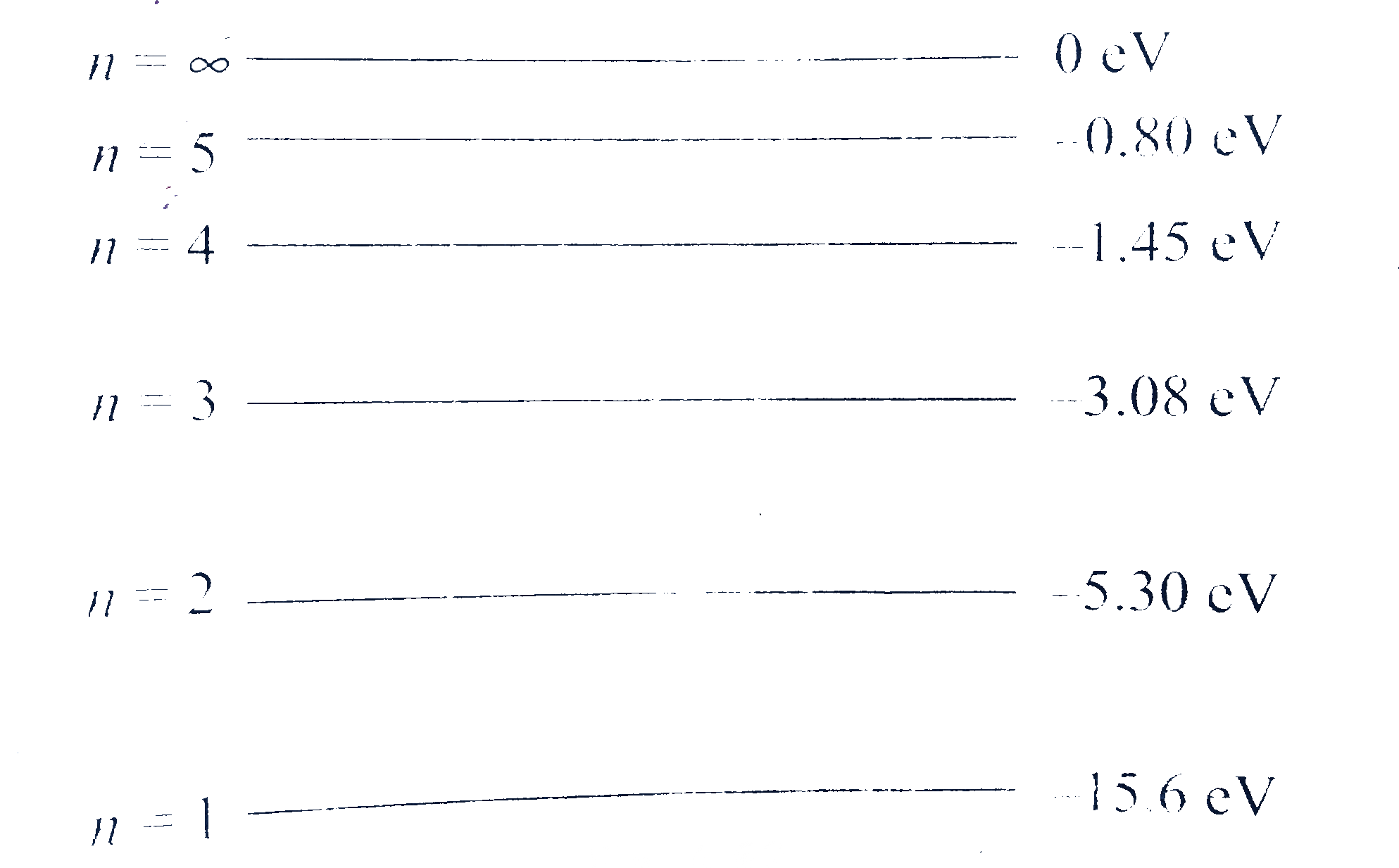
Find the excitation potential for the state `n = 3`.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
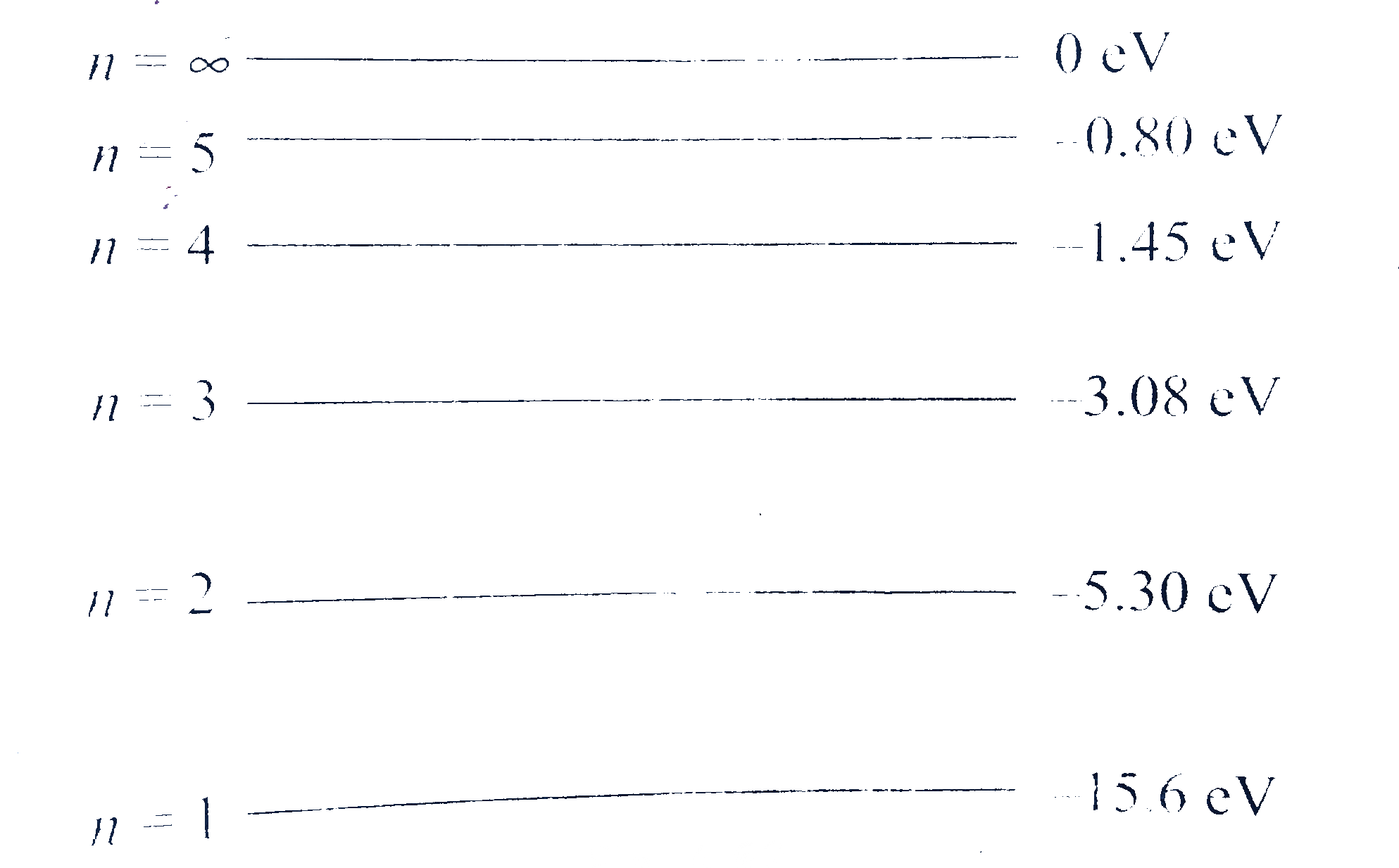
Find the wave number of the photon emitted for the transition `n = 3 to n = 1`
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
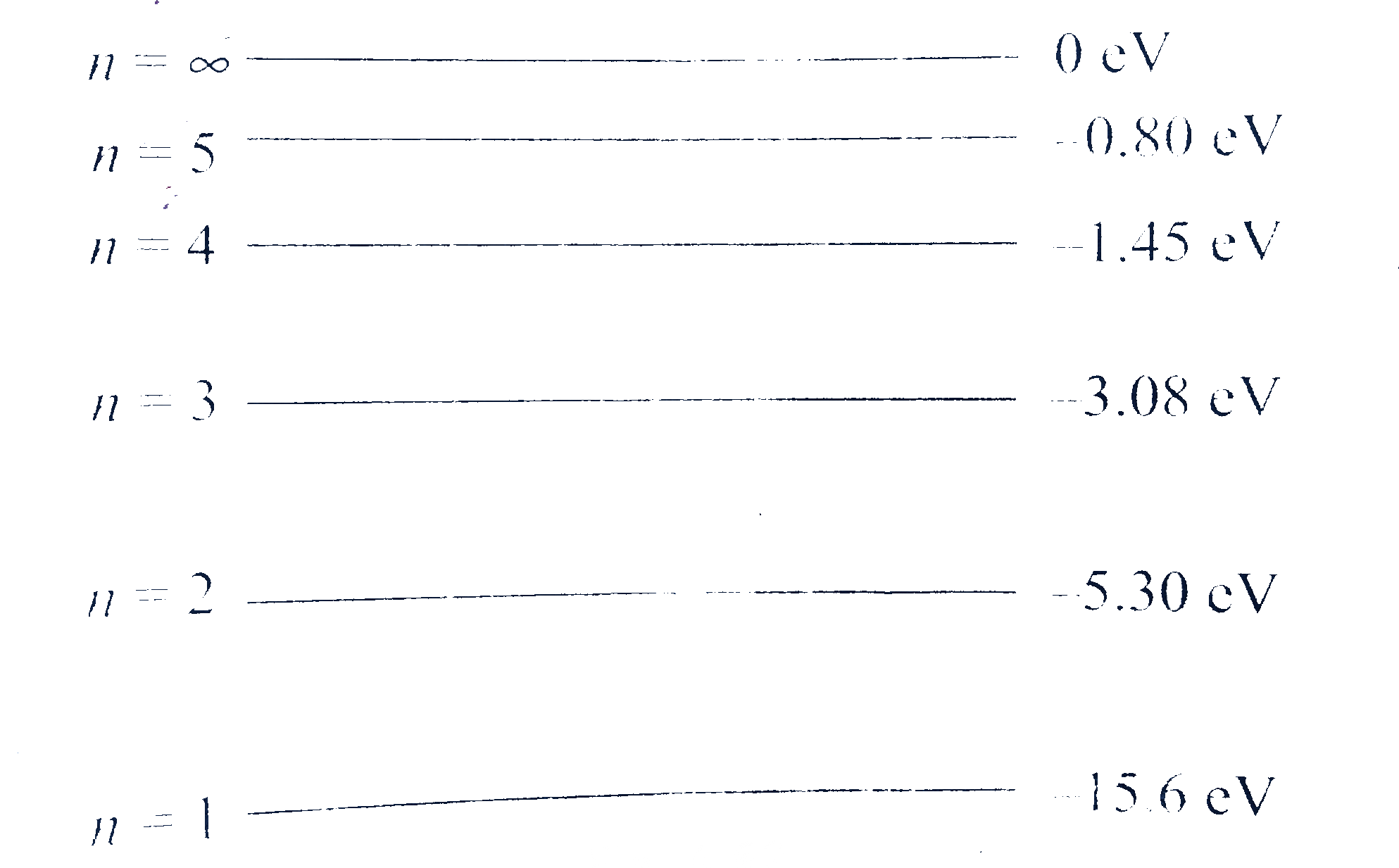
If an electron with initial kinetic energy `6 eV` is to interact with this hypothetical atom , what minimum energy will this electron carry after interaction?
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
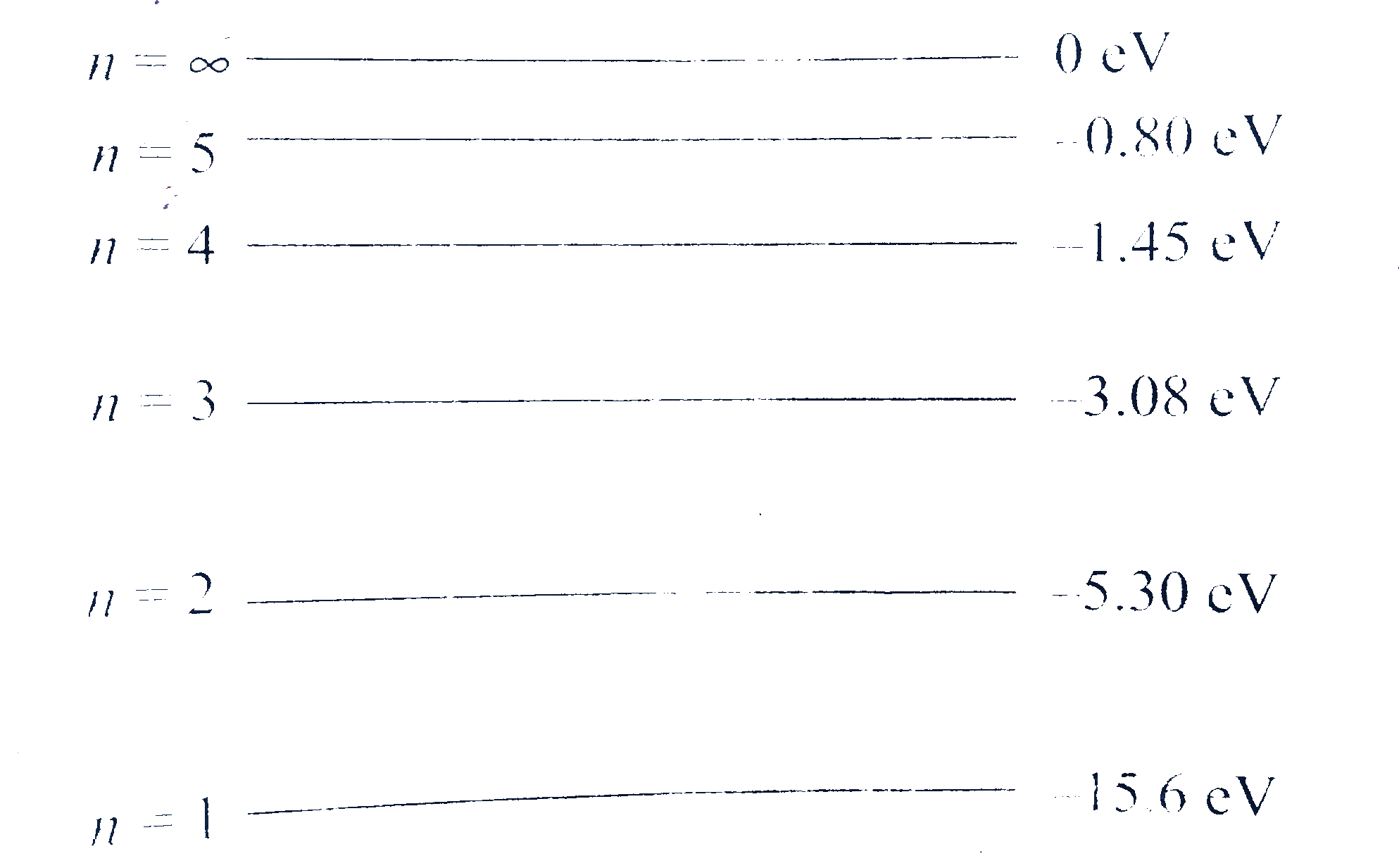
The initial kinetic energy of an electron is `11 eV` and it interact with the above said hypothetical one electron atom , the minimum energy carried by the electron after interaction is
View SolutionThe electron in a hydrogen atom at rest makes a transition from `n = 2` energy state to the `n = 1` ground state.
find the energy `(eV)` of the emitted photon.
View SolutionThe electron in a hydrogen atom at rest makes a transition from `n = 2` energy state to the `n = 1` ground state.
Assuming that all of the energy corresponding to transition from `n = 2 to n = 1` is carried off by the photon. By setting the momentum of the system (atom + photon) equal to zero after the emission and assuming that the recoil energy of the atom is smaller compared with the `n = 2 to n = 1` energy level separation , find the energy of the recoiling hydrogen atom.
View SolutionFor a certain hypothetical one electron atom, the wavelength `(in Å)` for the spectral lines for transitions originating at n=p and terminating at n=1 are given by `lambda = (1500 p^2)/(p^2 - 1), where p = 2,3,4`
(a)Find the wavelength of the least energetic and the most energetic photons in this series.
(b) Construct an energy level diagram for this element showing the energies of the lowest three levels.
(c ) What is the ionization potential of this element?
View SolutionFor a certain hypothetical one electron atom, the wavelength `(in Å)` for the spectral lines for transitions originating at n=p and terminating at n=1 are given by `lambda = (1500 p^2)/(p^2 - 1), where p = 2,3,4`
(a)Find the wavelength of the least energetic and the most energetic photons in this series.
(b) Construct an energy level diagram for this element showing the energies of the lowest three levels.
(c ) What is the ionization potential of this element?
View SolutionA sample of hydrogen gas in its ground state is irradiated with photons of `10.02 eV` energies. The radiation from the above sample is used to irradiate two other sample of excited ionized `He^(+)` and excited ionized `Li^(2+)`, respectively. Both the ionized samples absorb the incident radiation.
How many spectral lines are obtained in the spectra of `Li^(2+)`?
View SolutionA sample of hydrogen gas in its ground state is irradiated with photons of `10.02 eV` energies. The radiation from the above sample is used to irradiate two other sample of excited ionized `He^(+)` and excited ionized `Li^(2+)`, respectively. Both the ionized samples absorb the incident radiation.
What is the smallest wavelength that will be observed in spectra of `He^(+)` ion ?
View SolutionA sample of hydrogen gas in its ground state is irradiated with photons of `10.02 eV` energies. The radiation from the above sample is used to irradiate two other sample of excited ionized `He^(+)` and excited ionized `Li^(2+)`, respectively. Both the ionized samples absorb the incident radiation.
How many spectral lines are obtained in the spectra of `He^(+)` ion?
View SolutionA sample of hydrogen gas in its ground state is irradiated with photons of `10.02 eV` energies. The radiation from the above sample is used to irradiate two other sample of excited ionized `He^(+)` and excited ionized `Li^(2+)`, respectively. Both the ionized samples absorb the incident radiation.
Which is the smallest wavelength that will be observed in spectra of `Li^(2+)` ?
View SolutionA neutron of kinetic `6.5 eV` collides inelastically with a singly ionized helium atom at rest. It is scattered at an angle `90^(@)` with respect to its original direction.
Find the minimum allowed value of energy of the neutron.
View SolutionA neutron of kinetic `6.5 eV` collides inelastically with a singly ionized helium atom at rest. It is scattered at an angle `90^(@)` with respect to its original direction.
Find the maximum allowed value of energy of the He atom?
View SolutionSoppose potential energy between electronand proton at seperation `r` is given by `U = klog r, where k` is a constant. For such a hypothetical hydrogen atom , calculate the radins of nth Bohr and its energy level
View SolutionSuppose potential energy between electron and proton at separation `r` is given by `U = klog r`, where `k` is a constant. For such a hypothetical hydrogen atom , calculate the radius of nth Bohr and its energy level
View SolutionPertain to the following statement and figure

The figure above shown level diagram of the hydrogen atom. Serveral transition are market as I, II, III, … The diagram is only indicative and not to scale.
In which transition ia a Balmer series photon absorbed?
View SolutionPertain to the following statement and figure

The figure above shown level diagram of the hydrogen atom. Serveral transition are market as I, II, III, … The diagram is only indicative and not to scale.
The wavelength of the radiation involved in transition II is:
View SolutionPertain to the following statement and figure

The figure above shown level diagram of the hydrogen atom. Serveral transition are market as I, II, III, … The diagram is only indicative and not to scale.
Which transition will occur when a hydrogen atom is irradiated with radiation of wavelength `103 nm`?
View SolutionA certain species of ionized atoms produces emission line spectral according to the Bohr's model. A group of lines in the spectrum is forming a series in which in the shortest wavelength is `22.79 nm` and the longest wavelength is `41.02 nm`. The atomic number of atom is `Z`.
Based on above information, answer the following question:
The value of `Z` is
View SolutionA certain species of ionized atoms produces emission line spectral according to the Bohr's model. A group of lines in the spectrum is forming a series in which in the shortest wavelength is `22.79 nm` and the longest wavelength is `41.02 nm`. The atomic number of atom is `Z`.
Based on above information, answer the following question:
The series belongs to
View SolutionA certain species of ionized atoms produces emission line spectral according to the Bohr's model. A group of lines in the spectrum is forming a series in which in the shortest wavelength is `22.79 nm` and the longest wavelength is `41.02 nm`. The atomic number of atom is `Z`.
Based on above information, answer the following question:
The nesxt to longest wavelength in the series of lines is
View SolutionSimplified model of electron energy levels for a cartain atom is shown in figure. The atom is bombarded will fast moving electrons. The impact of one of these electrons can cause the removal of electron from K-level , thus, creating a vacancy in the K-level. This vacancy in K-level is filled by an electron from l-level and the energy reased in this transition can either appear as electromagnetic waves or may all be used knock out an electron from M-level of the atom.

Based on above information, answer the following question:
The minimum potential difference through which bombarding electron beam must be acclerated from rest to cause the ejection of electron from K-level is.
View SolutionSimplified model of electron energy levels for a cartain atom is shown in figure. The atom is bombarded will fast moving electrons. The impact of one of these electrons can cause the removal of electron from K-level , thus, creating a vacancy in the K-level. This vacancy in K-level is filled by an electron from l-level and the energy reased in this transition can either appear as electromagnetic waves or may all be used knock out an electron from M-level of the atom.

Based on above information, answer the following question:
Wavelength of the electromagnetic waves emitted due to transition from `L` to K-level is
View SolutionSimplified model of electron energy levels for a cartain atom is shown in figure. The atom is bombarded will fast moving electrons. The impact of one of these electrons can cause the removal of electron from K-level , thus, creating a vacancy in the K-level. This vacancy in K-level is filled by an electron from l-level and the energy reased in this transition can either appear as electromagnetic waves or may all be used knock out an electron from M-level of the atom.

Based on above information, answer the following question:
The `KE` of the emitted electron from M-level is
View SolutionA monochromatic beam of light having photon energy `12.5 eV` is incident on a simple `A` of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample `B` of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The atoms of sample `A` after passing of light through it
View SolutionA monochromatic beam of light having photon energy `12.5 eV` is incident on a simple `A` of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample `B` of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The emission spectra of sample `A`
View SolutionA monochromatic beam of light having photon energy `12.5 eV` is incident on a simple `A` of atomic hydrogen gas in which all almost are in the ground state. The emission spectra obtained from this sample is incident on another sample `B` of atomic hydrogen gas in which all atoms are in the first excited state.
Based on above information, answer the following question:
The atoms of sample `B`
View SolutionA single electron orbits a stationary nucleus of charge `+ Ze`, where `Z` is a constant and `e` is the magnitude of electronic charge . It requires `47.2 eV` to excite . Find
a the value of `Z`
b the energy required to excite the electron from the third to the fourth Bohr orbit.
the wavelength of electromagnetic rediation required to remove the electron from the first Bohr orbit to infinity.
d Find the `KE,PE`, and angular momentum of electron in the first Bohr orbit.
the redius of the first Bohr orbit
[The ionization energy of hydrogen atom `= 13.6 eV` Bohr radius `= 5.3 xx 10^(_11) m`, "velocity of light" `= 3 xx 10^(-8)jm s ^(-1)`, Planck's constant `= 6.6 xx 10^(-34)j - s]`
View SolutionA single electron orbits a stationary nucleus of charge `+ Ze`, where `Z` is a constant and `e` is the magnitude of electronic charge . It requires `47.2 eV` to excite . Find
a the value of `Z`
b the energy required to excite the electron from the third to the fourth Bohr orbit.
the wavelength of electromagnetic rediation required to remove the electron from the first Bohr orbit to infinity.
d Find the `KE,PE`, and angular momentum of electron in the first Bohr orbit.
the redius of the first Bohr orbit
[The ionization energy of hydrogen atom `= 13.6 eV` Bohr radius `= 5.3 xx 10^(_11) m`, "velocity of light" `= 3 xx 10^(-8)jm s ^(-1)`, Planck's constant `= 6.6 xx 10^(-34)j - s]`
View SolutionA single electron orbits a stationary nucleus of charge `+ Ze`, where `Z` is a constant and `e` is the magnitude of electronic charge . It requires `47.2 eV` to excite . Find
a the value of `Z`
b the energy required to excite the electron from the third to the fourth Bohr orbit.
the wavelength of electromagnetic rediation required to remove the electron from the first Bohr orbit to infinity.
d Find the `KE,PE`, and angular momentum of electron in the first Bohr orbit.
the redius of the first Bohr orbit
[The ionization energy of hydrogen atom `= 13.6 eV` Bohr radius `= 5.3 xx 10^(_11) m`, "velocity of light" `= 3 xx 10^(-8)jm s ^(-1)`, Planck's constant `= 6.6 xx 10^(-34)j - s]`
View SolutionWhen high energetic electron beam , (i.e., cathode rays) strike the heavier metal, then X-ray are produced. Spectrum of X-ray are classified into two categories: (i) continous spectrum, and (ii) characteristic depends only on the potential difference across the electrode. But wavelength of characteristic spectrum depends on the atomic number `(z)`.
The production of characteristic X-ray is due to the
View SolutionWhen high energetic electron beam , (i.e., cathode rays) strike the heavier metal, then X-ray are produced. Spectrum of X-ray are classified into two categories: (i) continous spectrum, and (ii) characteristic depends only on the potential difference across the electrode. But wavelength of characteristic spectrum depends on the atomic number `(z)`.
The production of continuous X-ray is due to the
View SolutionLight from a discharge tube containing hydrogen atoms falls on the surface of a piece of sodium . The kinetic energy of the fastest photoelectrons emitted from sodium is `0.73 eV` . The work function for sodium is `1.82 eV` find
(a) the energy of the photons causing the photoelectric emission ,
(b) the quantum number of the two level involved in the emission of these photons,
(c ) the change in the angular momentum of the electron in the hydrogen atom in the above transition and,
(d)the recoil speed of emitted atom assuming it to be at rest before the transition.
(lonization potential of hydrogen is `13.6 eV`)
View SolutionLight form a dicharge tube containing hydrogen atoms falls on the surface of a piece of sodium. The kinetic energy of the fastest photoelectrons emitted from sodium is 0.73 eV. The work function for sodium is 1.82 eV. Find (a) the energy of the photons causing the photoelectrons emission.
(b) the quantum numbers of the two levels involved in the emission of these photons.
(c ) the change in the angular momentum of the electron in the hydrogen atom, in the above transition, and
(d) the recoil speed of the emitting atom assuming it to be at rest before the transition. (lonization potential of hydrogen is 13.6 eV.)
View SolutionLight from a discharge tube containing hydrogen atoms falls on the surface of a piece of sodium . The kinetic energy of the fastest photoelectrons emitted from sodium is `0.73 eV` . The work function for sodium is `1.82 eV` find
(a) the energy of the photons causing the photoelectric emission ,
(b) the quantum number of the two level involved in the emission of these photons,
(c ) the change in the angular momentum of the electron in the hydrogen atom in the above transition and,
(d)the recoil speed of emitted atom assuming it to be at rest before the transition.
(lonization potential of hydrogen is `13.6 eV`)
View SolutionThe electron in a `Li^(+ +)` ion is the nth shell , `n` being very large. One of the K-electron in another matallic atom has been knocked out. The second matel has four orbits. Now, we take two sample one of `Li^(+ +)` ion and the other of the second mateillic ions. Suppose the probability of electronic transition from higher to lower energy level is directly proportional to the energy difference between the two shells. Take `hc = 1224 eV nm` , where `h` is Planck's constant and `c` the velocity of light in vacuum. It is found that major electromagnetic wavws emitted from the two sample are identical. Now , answer the following questions:
What is the X-ray having least intensity emitted by the second sample?
View SolutionThe electron in a `Li^(+ +)` ion is the nth shell , `n` being very large. One of the K-electron in another matallic atom has been knocked out. The second matel has four orbits. Now, we take two sample one of `Li^(+ +)` ion and the other of the second mateillic ions. Suppose the probability of electronic transition from higher to lower energy level is directly proportional to the energy difference between the two shells. Take `hc = 1224 eV nm` , where `h` is Planck's constant and `c` the velocity of light in vacuum. It is found that major electromagnetic wavws emitted from the two sample are identical. Now , answer the following questions:
What is the major X-ray emitted by the sample?
View SolutionThe electron in a `Li^(+ +)` ion is the nth shell , `n` being very large. One of the K-electron in another matallic atom has been knocked out. The second matel has four orbits. Now, we take two sample one of `Li^(+ +)` ion and the other of the second mateillic ions. Suppose the probability of electronic transition from higher to lower energy level is directly proportional to the energy difference between the two shells. Take `hc = 1224 eV nm` , where `h` is Planck's constant and `c` the velocity of light in vacuum. It is found that major electromagnetic wavws emitted from the two sample are identical. Now , answer the following questions:
The wavelength of this major X-ray is
View SolutionTwo hydrogen-like atoms `A` and `B` are of different masses and each atom contains equal numbers of protons and neutrons. The difference in the energies between the first Balmer lines emitted by `A and B` , is `5.667 e V`. When atom atoms `A and B` moving with the same velocity , strike a heavy target , they rebound with the same velocity in the process, atom `B` imparts twice the momentum to the target than that `A` imparts. Identify the atom `A and B`.
View SolutionTwo hydrogen-like atoms `A` and `B` are of different masses and each atom contains equal numbers of protons and neutrons. The difference in the energies between the first Balmer lines emitted by `A and B` , is `5.667 e V`. When atom atoms `A and B` moving with the same velocity , strike a heavy target , they rebound with the same velocity in the process, atom `B` imparts twice the momentum to the target than that `A` imparts. Identify the atom `A and B`.
View Solution`1.8 g` of hydrogen is excite by irradiation. The study of spectra indicated that `27 %` of the atoms are in the first excite state, `15 %` of the aton in the second excited, and the rest in the ground state. The ground stat, ionization energy of hydrogen atom is `21.4 xx 10^(-12)`ergs.
The number of atoms present in the second excited state is
View Solution`1.8 g` of hydrogen is excite by irradiation. The study of spectra indicated that `27 %` of the atoms are in the first excite state, `15 %` of the aton in the second excited, and the rest in the ground state. The ground stat, ionization energy of hydrogen atom is `21.4 xx 10^(-12)`ergs.
The total amount of energy that would be evolved when all the atoms neutron to the ground state is
View SolutionIn a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state `(n = 1)` are shown in the energy level diagram
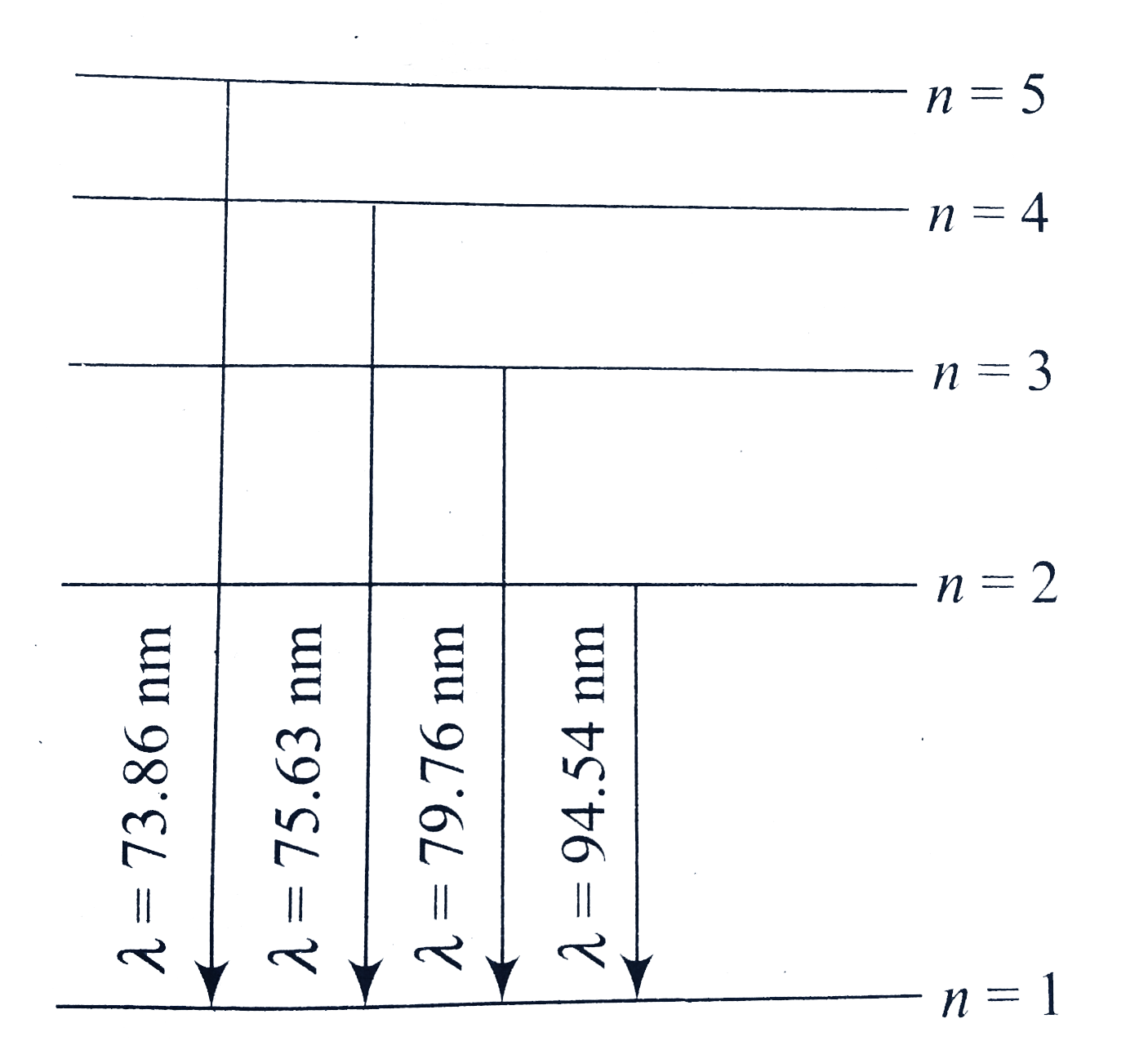
`lambda_(5 to 1) = 73.86 nm`
`lambda_(4 to 1) = 75.63 nm`
`lambda_(3 to 1) = 79.76 nm`
`lambda_(2 to 1) = 94.54 nm`
The energy of the atom in level `n = 1` is nearly
View SolutionIn a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state `(n = 1)` are shown in the energy level diagram
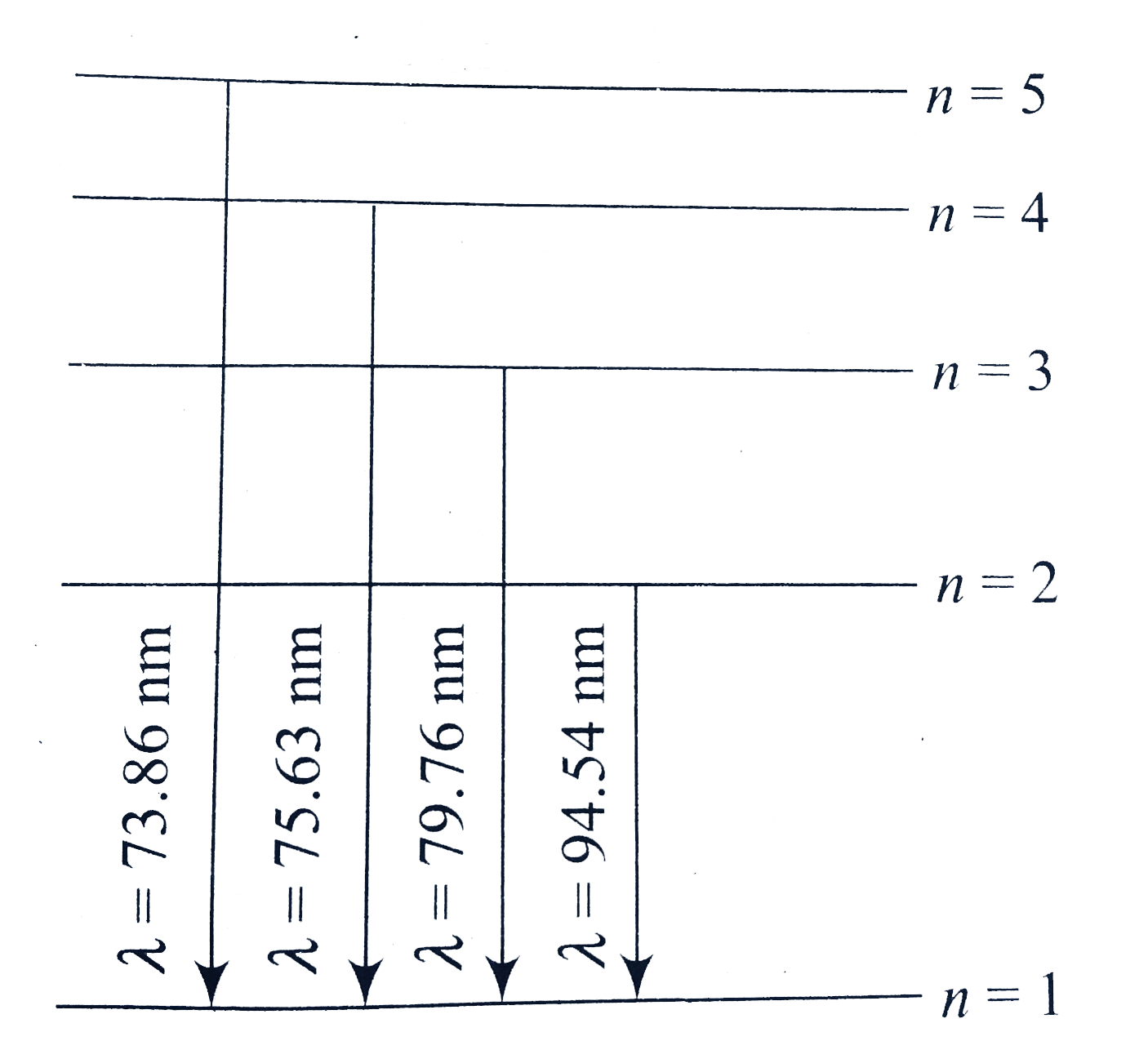
`lambda_(5 to 1) = 73.86 nm`
`lambda_(4 to 1) = 75.63 nm`
`lambda_(3 to 1) = 79.76 nm`
`lambda_(2 to 1) = 94.54 nm`
If an electron made a transition from `n = 4 to n = 2 level, the wavelength of the light that it would emit is nearly
View SolutionIn a set of experiment on a hydrogen on a hypothetical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state `(n = 1)` are shown in the energy level diagram
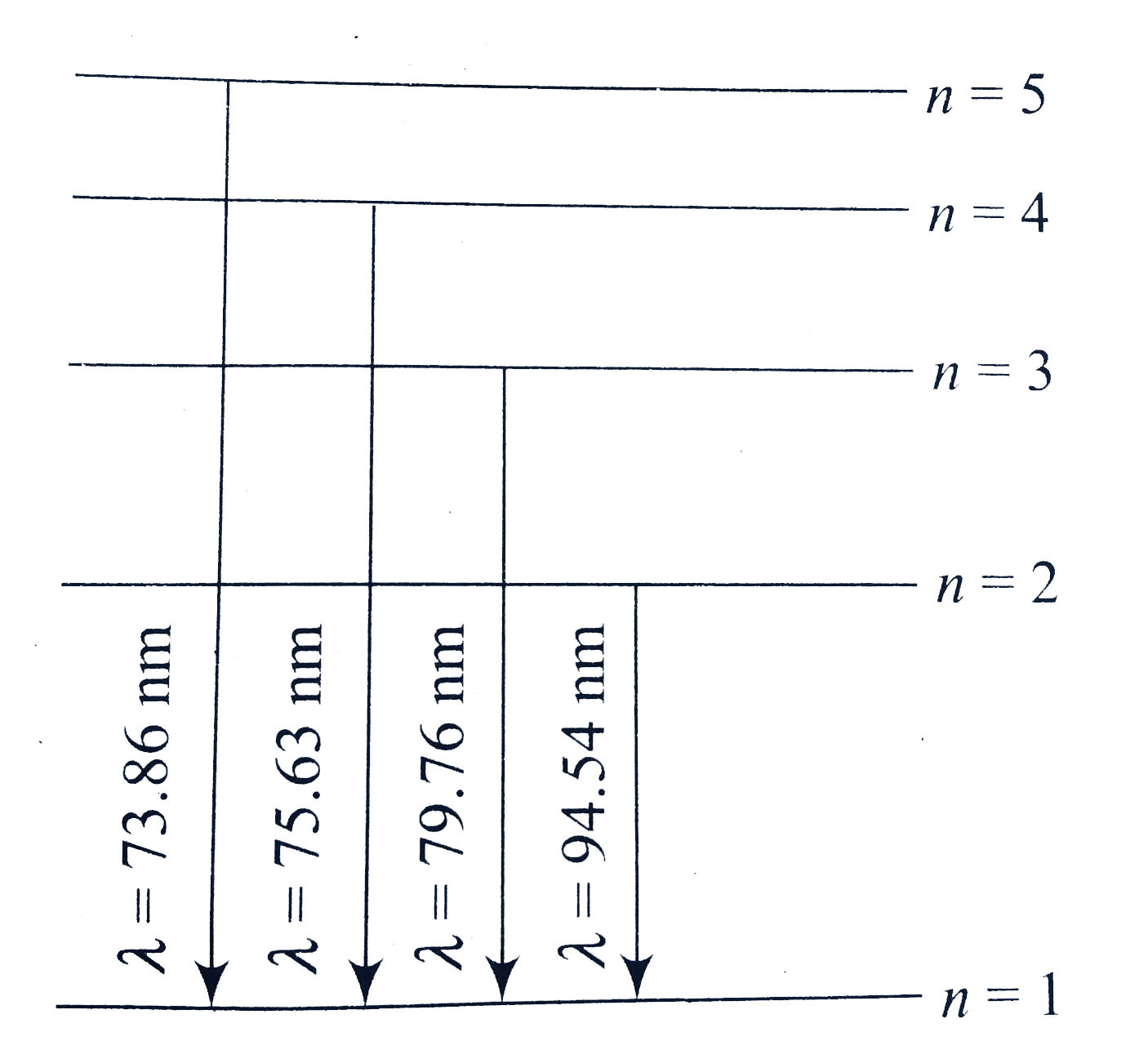
`lambda_(5 to 1) = 73.86 nm`
`lambda_(4 to 1) = 75.63 nm`
`lambda_(3 to 1) = 79.76 nm`
`lambda_(2 to 1) = 94.54 nm`
The possible energy of the atom in `n = 3` cannot be
View SolutionThe recoil speed of a hydrogen atom after it emits a photon is going form n=5 state to n =1 state is ….. m/s.
View Solution`K_alpha` wavelength emitted by an atom of atomic number Z=11 is `lambda`. Find the atomic number for an atom that emits `K_alpha` radiation with wavelength `4lambda`.
(a) Z=6 (b) Z=4
(c ) Z=11 (d) Z=44.
View SolutionAn electron in nth excited state in a hydrogen atom comes down to first excited state by emitting ten different wavelength. Find value of `n` (an integer).
View SolutionThe shortest wavelength of the Brackett series of a hydrogen-like atom (atomic number of `Z` ) is the same as the shortest wavelength of the Balmer series of hydrogen atom. The value of `z` is
View SolutionHeat at the rate of 200 W is produced in an X-ray tube operating at 20 kV. Find the current in the circuit. Assume that only a small fraction of the kinetic energy of electron is converted into X-rays.
View SolutionAn electron in an H-atom kept at rest , jumps from the nth shell to the nth shell `(m gt n)`. Suppose instead of emitting electromagnetic wave, the energy reased is converted into the kinetic energy of the atom. Assume the Bohr model and convervation of angular momentum are valid. If `l` is the moment of inertia the angular valocity of the atom about the nucleus is `4 (m - n) h // kl`. Calculate `k`
View Solution
Linked Comprehension questions and complete solutions for chapter ATOMIC PHYSICS of CENGAGE PHYSICS (HINGLISH) of Class 12