Complete Solutions to QUESTION BANK of chapter NUCLEI of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEI |
| CENGAGE PHYSICS | QUESTION BANK |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
The half lives of radioactive elements `X` and `Y` are `3` minute and `27` minute respectively. If the activities of both are same, then calculate the ratio of number of atoms of X and Y.
View SolutionThe radius of gemanium (Ge) moclide is measund w be
View SolutionInitial ratio of active nuclei in two different sample is 2: 3 their half lives are 2 hr and 3hr respectively . Ratio of their activities at the end of 12 hr is :
View SolutionThe radii of NUCLEI of two atoms are in ratio `(3)/(2)`. Assuming them to be hydrogen like atom, the ratio of their orbital radius for `(K)` shell is m/n .` Find `(m+n) .` (Assume number of proton `=` Number of neutron for each atom)
View SolutionThe fraction of a radioactive material which reamins active after time t is `9//16`. The fraction which remains active after time `t//2` will be .
View SolutionThe power obtained in a reactor using `U^(235)` disintergration is `1000kW`. The mass decay of `U^(235)` per hour is
View SolutionThe half-life of a radioactive isotope `X` is `50` years. It decays to another element `Y` which is stable. The two elements `X` and `Y` were found to be in the ratio of `1 : 15` in a sample of a given rock. The age of the rock was estimated to be
View SolutionObtain the amount of `( )_(27)^(60) (Co)` (in `mu (g)` ) necessary to provide a radioactive source of `8.0 (~m) (Ci)` strength. The half life of `( )_(27)^(60) (Co)` is `5.3` years. (Give answer in integer value)
View SolutionThe binding energy per nucleon of `underset(3)overset(7)Li` and `underset(2)overset(4) He`nuclet are `5.60 MeV` and `7.06 MeV`, respectively. In the nuclear reaction `underset(3)overset(7)Li+underset(1)overset(1) H rarr `underset(4)overset(2)He `, the value of energy `Q` (in MeV) released is
View SolutionIn the process of nuclear fission of `1g` of uranium, the mass lost is `0.90 mg`. The efficiency of fission reactor of power house is `20 %`. To obtain `400 MW` power from the power house, how much uranium (in gram) is required per hour?
View Solution`200 (MeV)` of energy can be obtained per fission. In a reactor generating `1000 kW`, the number of NUCLEI under going the fission per second is `3.125xx 10^(n)`. Find `n .`
View SolutionA nucleus of mass number 220 , initially at rest, emits an `alpha` -particle. If the `Q` value of the reaction is `5.5MeV`, the energy (in MeV) of the emitted `alpha` -particle will be
View SolutionA radioactive material decays by simulataneous emission of two particle from the with respective half - lives `1620` and `810` year . The time , in year , after which one - fourth of the material remains is
View SolutionIn an `alpha` -decay, the kinetic energy of `alpha`-particles is `48 MeV` and `Q` value of the reaction is `50 MeV`. The mass number of the mother nucleus is (assume that daughter nucleus is in ground state)
View SolutionThe distance of closest approach of a certain nucleus is 7.2 fm and it has a charge of `1.28 xx 10^(-17)` C. The number of neutrons inside the nucleus of an atom is
View SolutionThe activity of a fresh radioactive solution of volume 1 litre is `1200 Bq .` A volume `Delta V` of the same liquid has an activity `120 Bq` after three half lives. Then `Delta V` (in cc) must be
View SolutionTwo' radioactive samples `X` and `Y` having half life 3 years and 2 years, respectively, havẻ been decaying for many years. Today both samples have equal number of atoms. After how many years the number of atoms in the sample `X` will be twice of the number of atoms in the sample `Y` ?
View SolutionRadioactive NUCLEI `A` and `B` with half lives `T` and 21 , respectively, disintegrate into `C`. At `t=0`, number of NUCLEI of each `A` and `B` is `x`. The number of NUCLEI of `C` when rate of disintegration of `A` and `B` are equal is `alpha x`.
View SolutionGeiger counter reading of a radioactive sample is initially 6800 counts per minute. The same sample gives a reading of 425 counts per minute `10h` later. The half life of sample is `alpha` hours. Find `2 alpha`.
View SolutionA sample of `beta` active NUCLEI has a half life of `1.00` min. Initially, there are `10^(13) beta` active NUCLEI. Assuming that all the `beta` particles emitted leave the sample, what is the charge (in `mu C` ) acquired by the sample in 200 min?
View SolutionFor a substance, the average life for `alpha` -emission is 3240 years and for `beta` emission is 810 years. After how much time (in years) the one-fourth of the material remains by simultaneous emission? `(ln 2=0.693)` (Round of the answer to nearest integer.)
View SolutionA nucleus with mass number 220 , initially at rest, emits an `alpha` -particle. If the `Q` value of reaction is `7.8MeV` and subsequently after the emission of `alpha` -particle, a photon of energy `1.2 MeV` is also emitted, then the kinetic energy (in MeV ) of `alpha` -particle is.
View SolutionConsider the following 'fusion reaction: `underset(1)overset(2) H +`underset(1)overset(2)H rarr `underset(2)overset(4)He`. If `20 MeV of energy is released per fusion reaction and masss of ``underset(1)overset(2)H` consumed per day is `0.1 (~g)`, then what is the power of the reactor (in MW )? (Give answer in integer value)
View SolutionA radioactive sample `S_(1)` having the activity `A_(1)` has twice the number of nucleic as another sample `S_(2)` of activity `A_(2)`. If `A_(2)=2A_(1)`, then the ratio of half-life of `S_(1)` to the half-life of `S_(2)` is
View SolutionTwo radioactive elements R and S disintegrate as
`RtoP+alpha,lamda_(R)=4.5xx10^(-3)"years"^(-1)`
`StoQ+betal,lamda_(S)=3xx10^(-3)"years"^(-1)`
Starting with number of atoms of R and S in the ratio of 2:1 this ratio afte4r the lapse of three half lives of R will be
View SolutionThe radioactive sources `A` and `B`, initially containing the same number of radioactive atoms, have half lives of `2h` and `4h`, respectively. At the end of `2h`, their rates of disintegration are in the ratio `sqrt((p)/(q))`. Find `(p+q)`.
View SolutionA nucleus `X`, initially at rest, decays into a nucleus `Y` with the emission of an `alpha` -particle'and energy `Q` is released. If `m` is mass of `alpha` -particle and `M` that of rucleus `Y`, the energy of the emitted `alpha` -particle is given by `E_(alpha)=(Q M)/(M+x m) .` Find the value of `x`.
View SolutionThe graph represents the decay of a newly prepared sample of radioactive nuclide `X` to a stable nuclide `Y .` The half life of `X` is `tau`. The growth curve for `Y` intersects the decay curve for `X` after time `T .` What is the time `T` in multiple of `tau` ?
'(## CEN_KSR_PHY_JEE_CO30_E01_028_Q01##)'
View SolutionThe threshold energy (in `(MeV)` ) for the following nuclear reaction to proceed is
`underset(2)overset(4)He + `underset(7)overset(14)N rarr `underset(8)overset(17)O + `underset(1)overset(1)H`
Atomic,mass of `underset(2)overset(4)He = 4.00260 amu` Atomic mass of `underset(7)overset(14)N=14.00307 amu` Atomic mass of `underset(8)overset(17)Li`=16.99913 (amu)` Atomic mass of `underset(1)overset(1)H=1.00783 (amu)`
View SolutionHalf life of a radioactive substance is `2.34 min`. It is produced at'a constant rate of `10^(8)` NUCLEI per second. How soon (in minute) after the beginning of production will its activity be equal to disintegration per second?
View SolutionA radioactive sample has a half life of `40s`. When its activity is measured `80s` after the beginning, it is found to be `6.932 xx 10^(18)` dps. During this time, total energy released is `6 xx 10^(8) J`. If the energy released per fission is `yxx10^(-13)` joule, then find `y .(ln 2=0.6932)`
View SolutionA moving neutron collides with stationary H-atom in ground state. As a result it excites and then de-excites. The corresponding radiation fail on a surface having work function `sigma`. The minimum value of required kinetic energy for neutron is `E_(0)` and possible minimum value of de-Broglie wavelength of emitted photoelectrons is `lambda_(0)`. If the neutron hits stationary `(He)^(+)` ion instead of stationary `(H)` atom, then the minimum value of kinetic energy for neutron is `E_(1)` and the value of energy. transferred from neutron to H-atom is `(x E_(0))/(y) .` Find `(x y)`.
View SolutionOne possible method for revealing the presence of concealed nuclear weapons is to detect the neutrons emitted in the spontaneous fission of `overset(240)Pu` in the warhead. In an actual trial, a neutron detector of radius `1.0 m` carried on a helicopter measured a neutrón flux of `50s^-1` at a distance of `100 m` from a missile warhead. Estimate the mass of `overset(240)Pu` (in kg ) in the warhead. The mean life for spontaneous fission in `overset(240)Pu` is `6xx 10^(18) s`, and `2.5` neutrons on the average are emitted in each fission. (Avogadro's number `=6 times 10^(23)` )
View SolutionFor a substance, the average life for `alpha` -emission is 1620 years and for `beta` emission is 405 years. If after `(k xx 0.693)` years, the one-fourth of the material remains by simultaneous emission, then find `k`
View SolutionA radioactive sample decays by ' `beta` -emission. In first 2 seconds, `n beta` -particles are emitted and in next 2 seconds, `0.25 n beta` -particles are emitted. The half life of radioactive NUCLEI (in second) is
View SolutionThe graph in the figure shows how the count-rate `A` of adioactive source as measured by a Geiger counter varies with time `t`. The relationship between `A` and `t` is `A=k e^(-0.1 t) .` Find `k`. (Assume ln12=2.6)`
'(## CEN_KSR_PHY_JEE_CO30_E01_036_Q02##)'
View SolutionConsider a nuclear fusion reaction `A+B rarr C .` Nucleus `A` is moving with kinetic energy `=5 MeV` and collides with mucleus `B` moving with kinetic energy `=3 MeV and forms 'nucleus `C` in excited state. Find the kinetic energy (in MeV) of núcleus `C` just after its formation given that its excitation energy is `10.3 MeV`. Take masses of NUCLEI of `A, B` and `C` as `25.0 amu, 10.0 amu, 34.99 amu`, respectively. (1 amu=930 MeV )
View SolutionThe positions of `underset(1)overset(2)D, underset(2)overset(4)He` and `underset(3)overset(7)Li`are shown on the binding energy curve as shown in the figure. Find the energy released (in multiple of `2 (MeV)` ) in the fusion reaction, `underset(1)overset(2)D + `underset(3)overset(7)Li rarr 2`underset(2)overset(4)He + underset(o)overset(1)n`
'(## CEN_KSR_PHY_JEE_CO30_E01_038_Q03##)'
View SolutionA radioactive sample contains two radionuclids `A` and `B` having décay constant `lambda h^(-1)` and `2 lambda h ^(-1) .` Initially, `25 %` of total decay comes from `A`. How long (in h ) will it take before `75 %` of total decay comes from `A`. (Take `lambda=ln 3)`
View SolutionConsider the following process of decays
`underset(92)overset(234)U rarr underset(90)overset(230)Th + underset(2)overset(4)He, T_(1/2) = 250000 years`
`underset(90)overset(230)Th rarr underset(88)overset(226)Ra + underset(2)overset(4) He , T_(1/2) = 80000 years`
`underset(226)overset(88) Ra rarr underset(222)overset(86)Rn + underset(2)overset(4)He , T_(1/2) = 1600 years` After above process has occurred for a long time, a state is reached where every two thorium atoms formed from `underset(92)overset(234)U`, one decomposes to form `underset(88)overset(226)Rn` and for every two`underset(88)overset(226)Ra` formed, one decomposes to form ``underset(222)overset(86)Rn` .Calculate the ratio of number of NUCLEI of `underset(90)overset(230)Th` to ``underset(88)overset(226)Ra` at this state.
View SolutionThe friction of a radioactive sample which remains active aftertime `t` is `(9)/(16) .` What friction remains active after `(t)/(2)` time?
View SolutionThe power obtained in a reactor using `U^(235)` disintergration is `1000 kW`. The mass decay of `U^(235)` per hour is (in `mu g` )
View SolutionThe half life of a radioactive isotope `X` is 50 years. It decays to another element `Y` which is stable. The two elements `X` and `Y` were found to be in the ratio of 1: 15 in a sample of a given rock. The age (in years) of the rock was estimated to be
View SolutionObtain the amount of `( )_(27)^(60) (Co)` (in `mu (g)` ) necessary to provide a radioactive source of `8.0 (~m) (Ci)` strength. The half life of `( )_(27)^(60) (Co)` is `5.3` years. (Give answer in integer value)
View SolutionThe binding energy per nucleon of `._(3)^(7) Li` and `._(2)^(4)He` nuclei are `5.60` MeV and `7.06` MeV, respectively. In the nuclear reaction `._(3)^(7)Li+._(1)^(1)H rarr ._(2)^(4)He+._(2)^(4)He+Q`, the value of energy `Q` released is
View SolutionIn the process of nuclear fission of `1g` of uranium, the mass lost is `0.90 mg`. The efficiency of fission reactor of power house is `20 %`. To obtain `400 MW` power from the power house, how much uranium (in gram) is required per hour?
View Solution`200 (MeV)` of energy can be obtained per fission. In a reactor generating `1000 kW`, the number of NUCLEI under going the fission per second is `3.125xx 10^(n)`. Find `n .`
View SolutionA nucleus of mass number 220 , initially at rest, emits an `alpha` -particle. If the `Q` value of the reaction is `5.5MeV`, the energy (in MeV) of the emitted `alpha` -particle will be
View SolutionA radioactive material decays by simultaneous emission of two particles of half lives 1620 and 810 years. The time (in years) after which one-fourth of the material remains, is
View SolutionIn an `alpha` -decay, the kinetic energy of `alpha` particle is `48 (MeV)` and `Q` value of the reaction is `50MeV`. The mass number of the mother nucleus is (Assume that daughter nucleus is in ground state).
View SolutionThe nuclear radius of a certain nucleus is `7.2 fm` and it has charge of `1.28xx 10^(-17) (C)`. Find the number of neutrons inside the nucleus.
View SolutionFor a substance, the average life for `alpha` -emission is 3240 years and for `beta` emission is 810 years. After how much time (in years) the one-fourth of the material remains by simultaneous emission? `(ln 2=0.693)` (Round of the answer to nearest integer.)
View SolutionA nucleus with mass number 220 , initially at rest, emits an `alpha` -particle. If the `Q` value of reaction is `7.8MeV` and subsequently after the emission of `alpha` -particle, a photon of energy `1.2 MeV` is also emitted, then the kinetic energy (in MeV ) of `alpha` -particle is.
View SolutionA radioactive sample `S_(1)` having the activity `A_(1)` has twice the number of NUCLEI as another sample `S_(2)` of activity `A_(2)` : If `A_(2)=2 A_(1)`, then the ratio of half life of `S_(1)` to the half life of `S_(2)` is
View SolutionTwo radioactive elements `R` and `S` disintegrate as `R rarr P+alpha , lambda_(R)=4.5 xx 10^(-3)` years `^(-1)` `S rarr P+beta , lambda_(s)=3 xx 10^(-3)` years `^(-1)`
Starting with number of atoms of `R` and `S` in the ratio of `2: 1`, this ratio after the lapse of three half lives of `R` will be
View SolutionThe radioactive sources `A` and `B`, initially containing the same number of radioactive atoms, have half lives of `2h` and `4h`, respectively. At the end of `2h`, their rates of disintegration are in the ratio `sqrt((p)/(q))`. Find `(p+q)`.
View SolutionThe graph represents the decay of a newly-prepared sample of radioactive nuclide X to a stable nuclide Y. The half-life of X is t. The growth curve for Y intersects the decay curve for X after time T. What is the time T ?
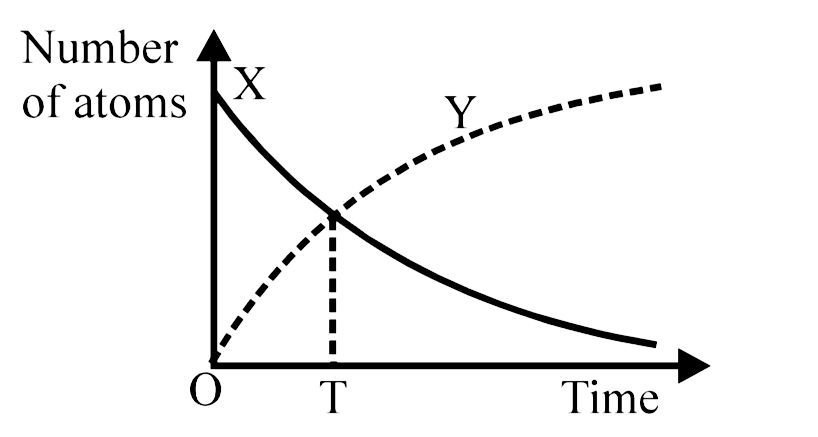
View SolutionFor a substance, the average life for `alpha` -emission is 1620 years and for `beta` emission is 405 years. If after `(k xx 0.693)` years, the one-fourth of the material remains by simultaneous emission, then find `k`
View SolutionA radioactive sample decays by ' `beta` -emission. In first 2 seconds, `n beta` -particles are emitted and in next 2 seconds, `0.25 n beta` -particles are emitted. The half life of radioactive NUCLEI (in second) is
View Solution
QUESTION BANK questions and complete solutions for chapter NUCLEI of CENGAGE PHYSICS (HINGLISH) of Class 12