Complete Solutions to Example of chapter CURRENT ELECTRICITY of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | CURRENT ELECTRICITY |
| DC PANDEY NEET | Example |
| Number Of Questions | 61 |
| Academic Year | 2023-24 |
How many electrons pass through a bulb in 1 min, if the current is 400 mA `(e=1.6xx10^(-19)C)`?
View Solution`10^(20)` electrons, each having a charge of `1.6xx10^(-19)` C, pass from a point A towards another point B in 0.1 s. What is the current in ampere ? What is its direction ?
View SolutionA wire carries a current of `2.0A`. What is charge that has flowed through is cross section in `1.0s`? How many electrons does his correspond to?
View SolutionIf an elctron revolves in a circle of radius `pi//2` cm with uniform speed `6xx10^(5)m//s`. Find the electric currect. (Take, `pi^(2)=10`)
View Solution(a) The amount of charge passed in time `t` through a cross-section of wire is
`q = alpha t - beta t^2`
where `alpha` and `beta` are constant.
(i) Find current in terms of time `t`.
(ii) Sketch `i` versus `t` graph.
(b) The current through a wire depends on time as
`i = 4 + 3t + 2t^2`
Find the charge crossed through a section of wire in `6 sec`.
View SolutionThe current in a wire varies with time according to the relation `i=(3.0A)+(2.0A//s)t`
a. How many coulomns of charge pass a cross section of the wire in the time internal between `t=0` and `t=4.0s`?
b. What constant current would transport the same charge in the same time interval?
View SolutionAn electron beam has an aperture of `2mm^(2)`. A total of `7xx10^(16)` electrons flow through any perpendicular cross-section per second. Calculate the current density in the electron beam.
View SolutionFind the current flowing through a copper wire of length 0.2m, area of cross-section `1 mm^(2)`, when connected to a battery of 4 V. Given that electron mobility `=4.5xx10^(-6) m^(2)V^(-1) s^(-1)` and charge on electron `=1.6xx10^(-19)C`. The number density of electron in copper is `8.5 xx10^(28) m^(-3)`.
View SolutionAn aluminium wire of diameter 0.24 cm is connected in series to a copper wire of diameter 0.16 cm. The wires carry an electric current of 10 ampere. Find (i) current-density in the aluminium wire (ii) drift velocity of electrons in the copper wire. Given : Number of electrons per cubic metre volume of copper `=8.4xx10^(28)`.
View SolutionWhat is the drift velocity of electrons in a silver wire of length 2 m, having cross-sectional area `6.14xx10^(-6)m^(2)` and carrying a current of 5A. Given, atomic weight of silver = 108, density of silver `=9.5xx10^(3)kg//m^(3)`, charge of electron `=1.6xx10^(-9)C`, Avogadro's number `=6.023xx10^(26)` per kg atom?
View SolutionThe resistance of a wire is R ohm. What will be its new resistance if it is stretched to n times its original length ?
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionAll the edges of a block with parallel faces are unequal. Its longest edge is twice its shortest edge. The ratio of the maximum to minimum resistance between parallel faces is.
View SolutionCalculate the electric field in a copper wire of cross-sectional area`2.0mm^(2)` carrying a current of 1A .The resistivity of copper `=1.7xx10^(-8)(Omega)m`.
View SolutionA copper wire has a resistance of `10 Omega ` and an area of cross-section `1 mm^(2)`. A poetential difference of 10 V exists across the wire. Calculate the drift speed of electrons if the number of electrons per cubic metre in copper is `8xx10^(28)` electrons.
View SolutionA current of 1.0 ampere is flowing through a copper wire of length 0.1 metre and cross-section `1.0xx10^(-6) m^(2)`. (i) If the specific resistance of copper be `1.7xx10^(-8) Omega m`, calculate the potential difference across the ends of the wire. (ii) Determine current density in the wire. (iii) If there be one free electron per atom in copper, then determine the drift velocity of electrons. Given : density of copper `=8.9xx10^(3) kg m^(-3)`, atomic weight`=63.5, N=6.02xx10^(26)` per kg-atom.
View SolutionFind the relaxation time for free electrons in copper, if the density of mobile electrons in copper, if the density of mobile electrons is `8.4 xx10^(28) m^(-3)`. The resistivity of copper at room temperature is `1.7xx10^(-8)Omega m`.
Given : mass of electron `=9.11 xx10^(-31) kg ` and charge on electron `=1.6xx10^(-19)C`.
View SolutionA wire has a resistance R. Find new resistance,
(i) if radius of cross-section of a cylindrical wire is doubled, then find ratio of initial to final resistance.
(ii) if length of wire is increased by `10%`, then find the percentage increase in its resistance.
(iii) if length of wire is increased by `20%`, then find the percentage increase in its resistance.

View SolutionThe resistance of a thin silver wire is `1.0 Omega` at `20^@C`. The wire is placed in a liquid bath and its resistance rises to `1.2 Omega`. What is the temperature of the bath? `alpha` for silver is `3.8xx10^03//(.^(@) C)`
View SolutionResistance of platinum wire in a platinum resistance thermometer at melting ice, boiling water and at a hot bath are `6Omega,6.5Omega` and `6.2Omega`, respectively. Find temperature of hot bath.
View SolutionThe temperature coefficient of resistance of a wire is `0.00145^(@)C^(-1)`. At `100^(@)C` its resistance is `2Omega`. At what temperature the resistance of the wire be `3Omega`?
View SolutionHow will you repersent a resistance of `3700 Omega +- 10%` by colour code?
View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
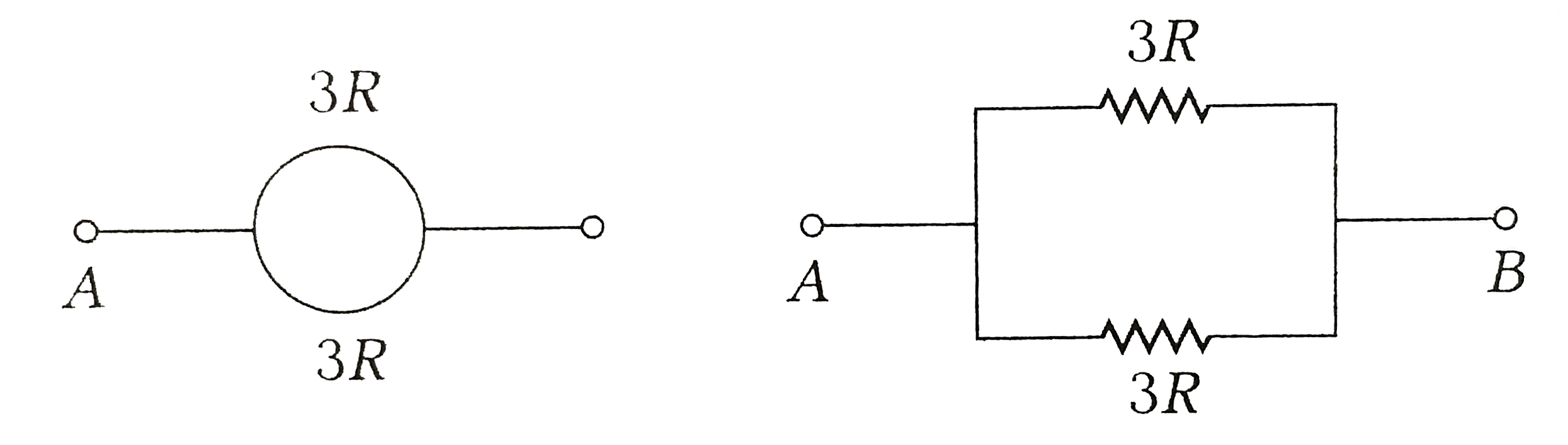
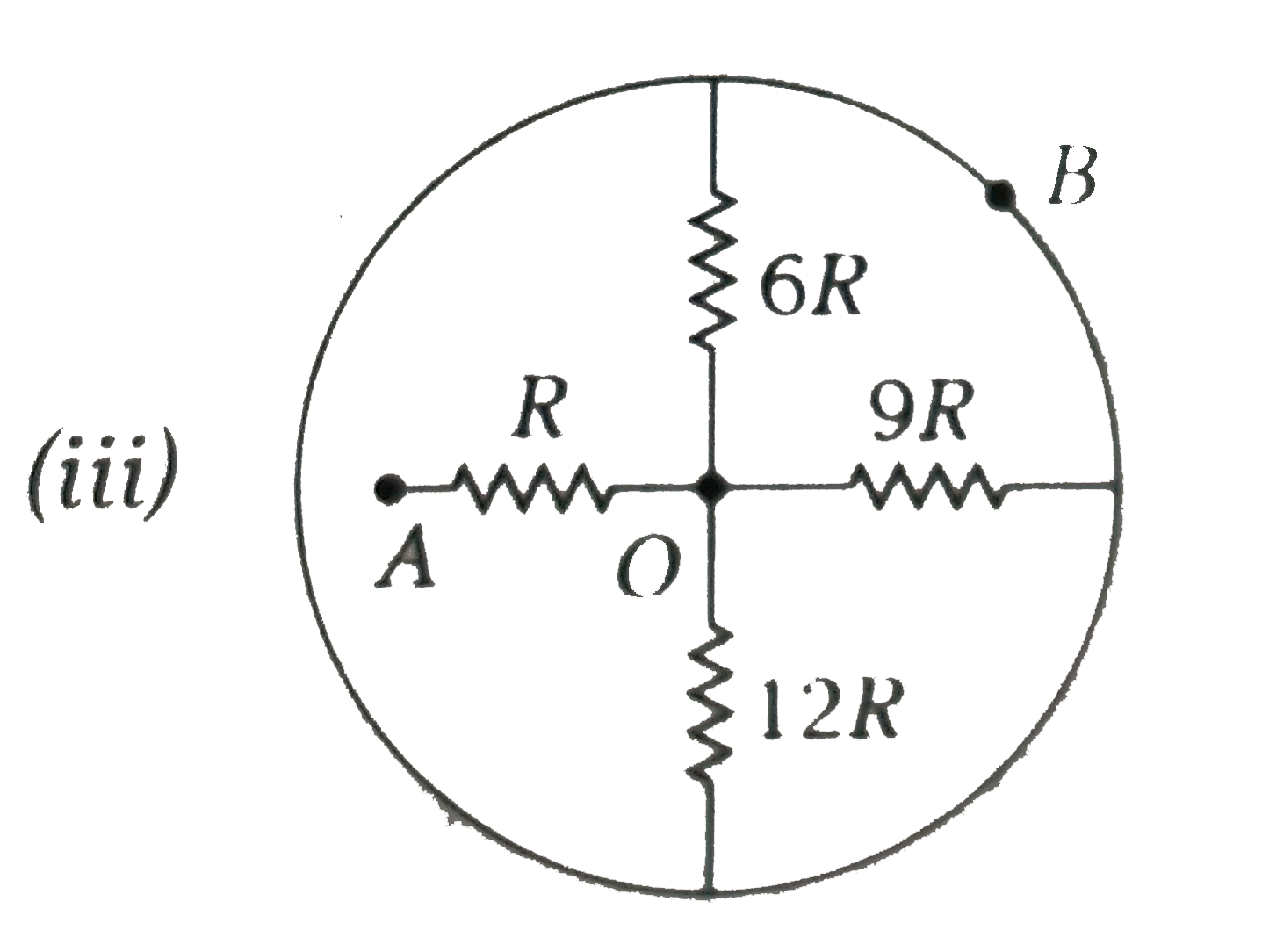
View SolutionFind the equivalent resistance between A and B in the following cases
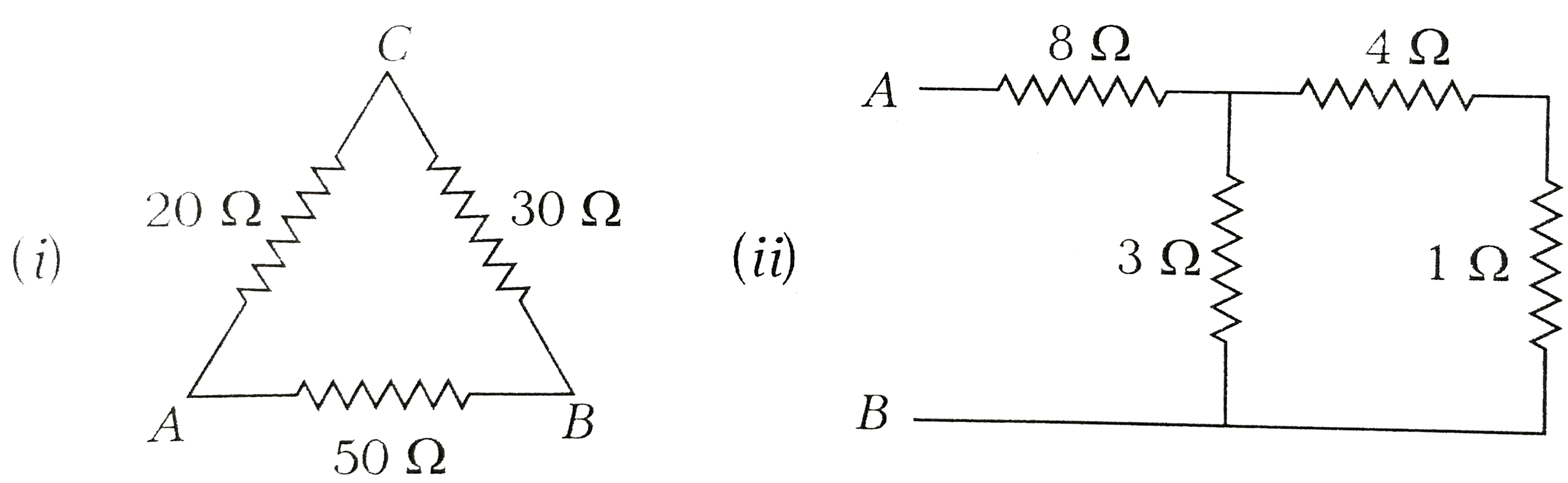
View SolutionA letter A consists of a uniform wire of resistance 1 ohm per cm. The sides of the letter are each 20 cm long and the cross-piece in the middle is 10 cm long while the apex angle is `60^(@)`. Find the resistance of the letter between the two ends of the legs.
View SolutionFind in the given network of resistors, the equivalent resistance between the points A and B, between A and D.

View SolutionFind the effective resistance between points A and B for the network shown in the figure below.
`(ARH_NEET_PHY_OBJ_V02_C03_S01_027_Q01.png" width="80%">
View SolutionFind the equivalent resistance between A and B in the following case

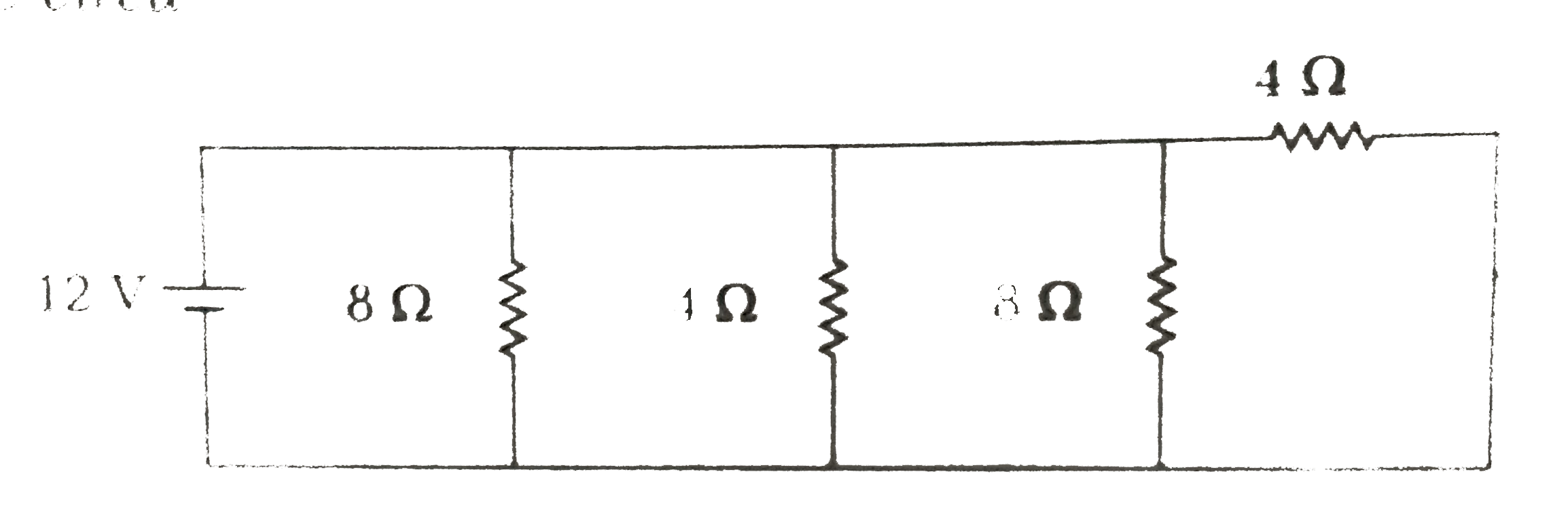
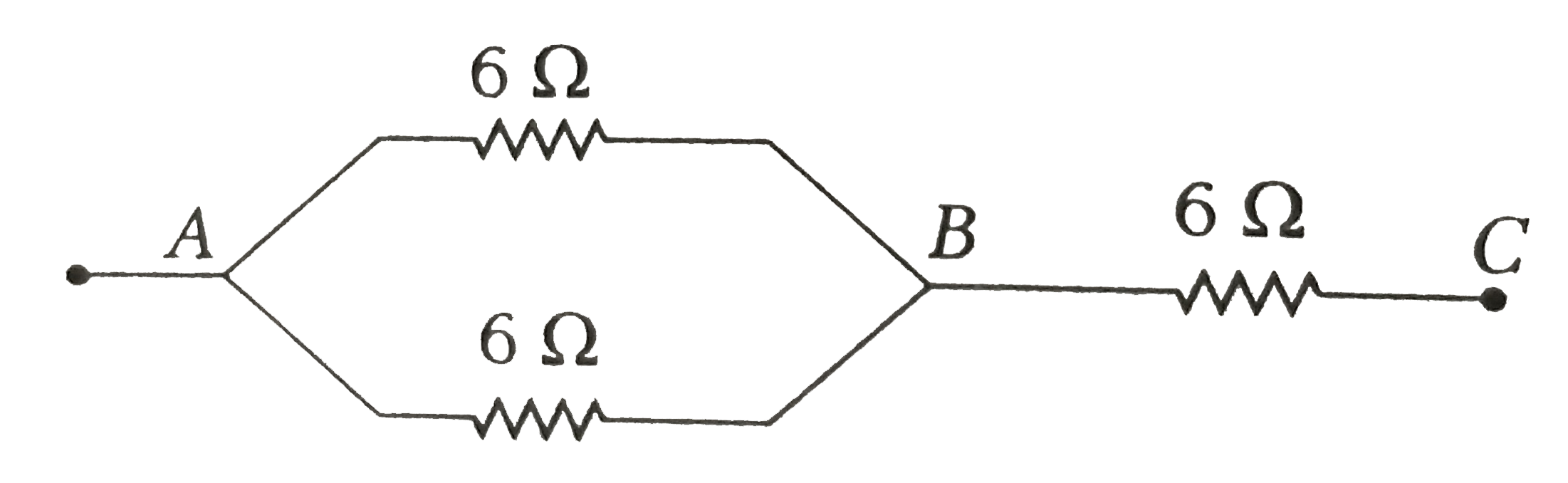
View SolutionFind the equivalent resistance between A and B.

View SolutionDetermine the current supplied by the battery in the circuit as shown
(ii) Find currents in resistance `2Omega` and `4Omega`.

View SolutionCalculate the current shown by the ammeter A in the circuit shown in figure.
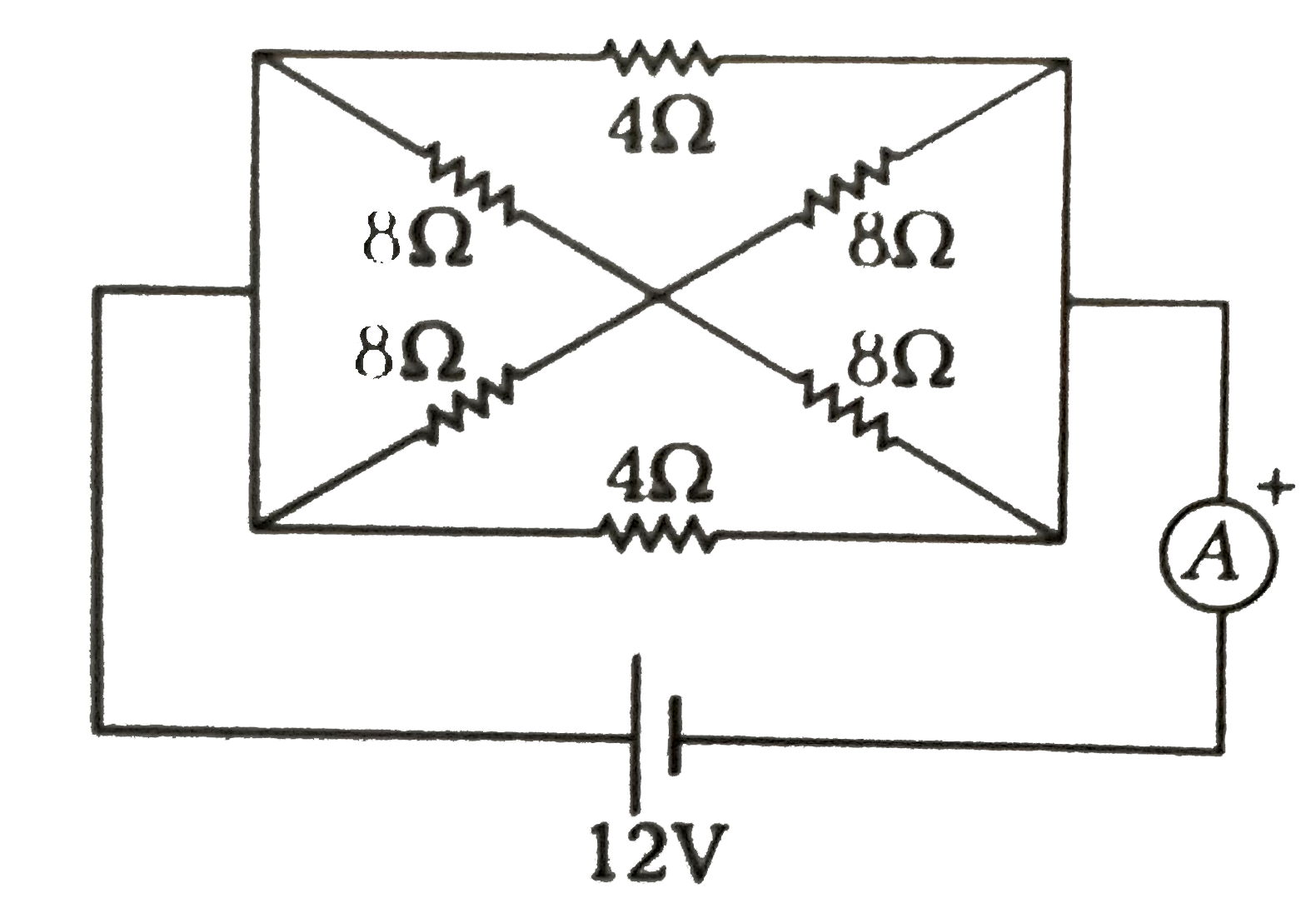
View SolutionFind the equivalent resistance between A and B.
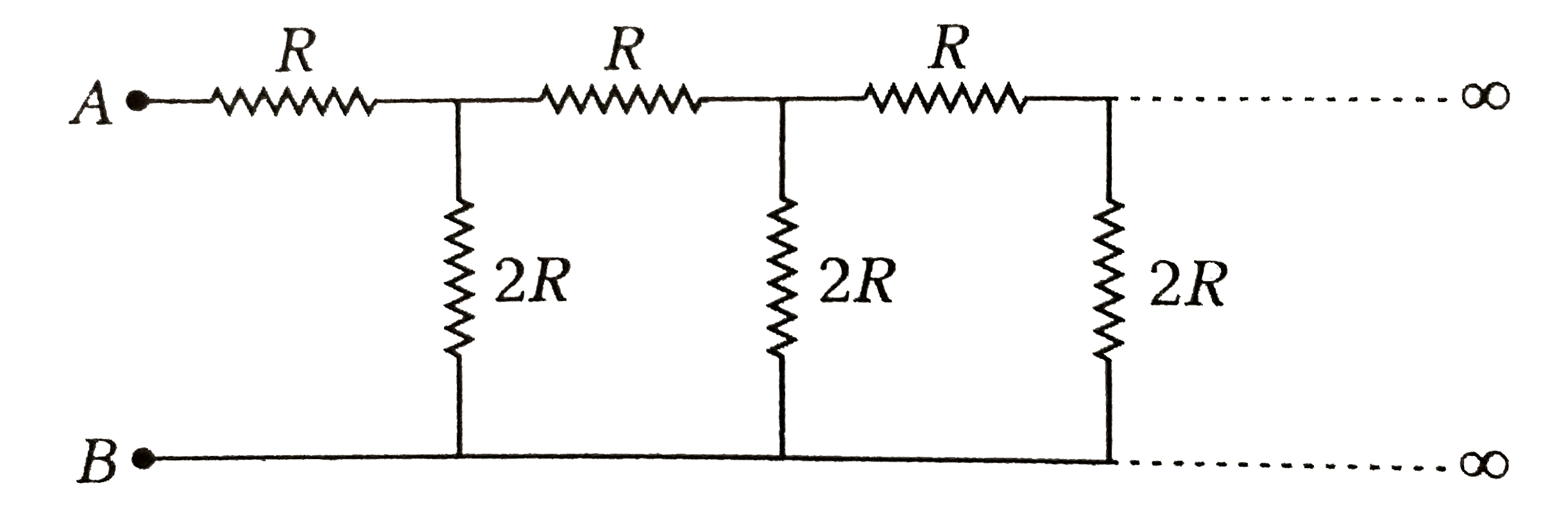
View SolutionThe reading on a high resistance voltmeter when a cell is connected across it is 3 V. When the terminals of the cell are also connected to a resistance of 4 `Omega`, then the voltmeter reading drops to `1.2` V. Find the internal resistance of the cell.
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of `10Omega` through an ammeter of resistance `2Omega`. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View SolutionA voltmeter of resistance `994Omega` is connected across a cell of emf 1 V and internal resistance `6Omega`. Find the potential difference across the voltmeter, that across the terminals of the cell and percantage error in the reading of the voltmeter.
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance `2 Omega` connected to the network given below.
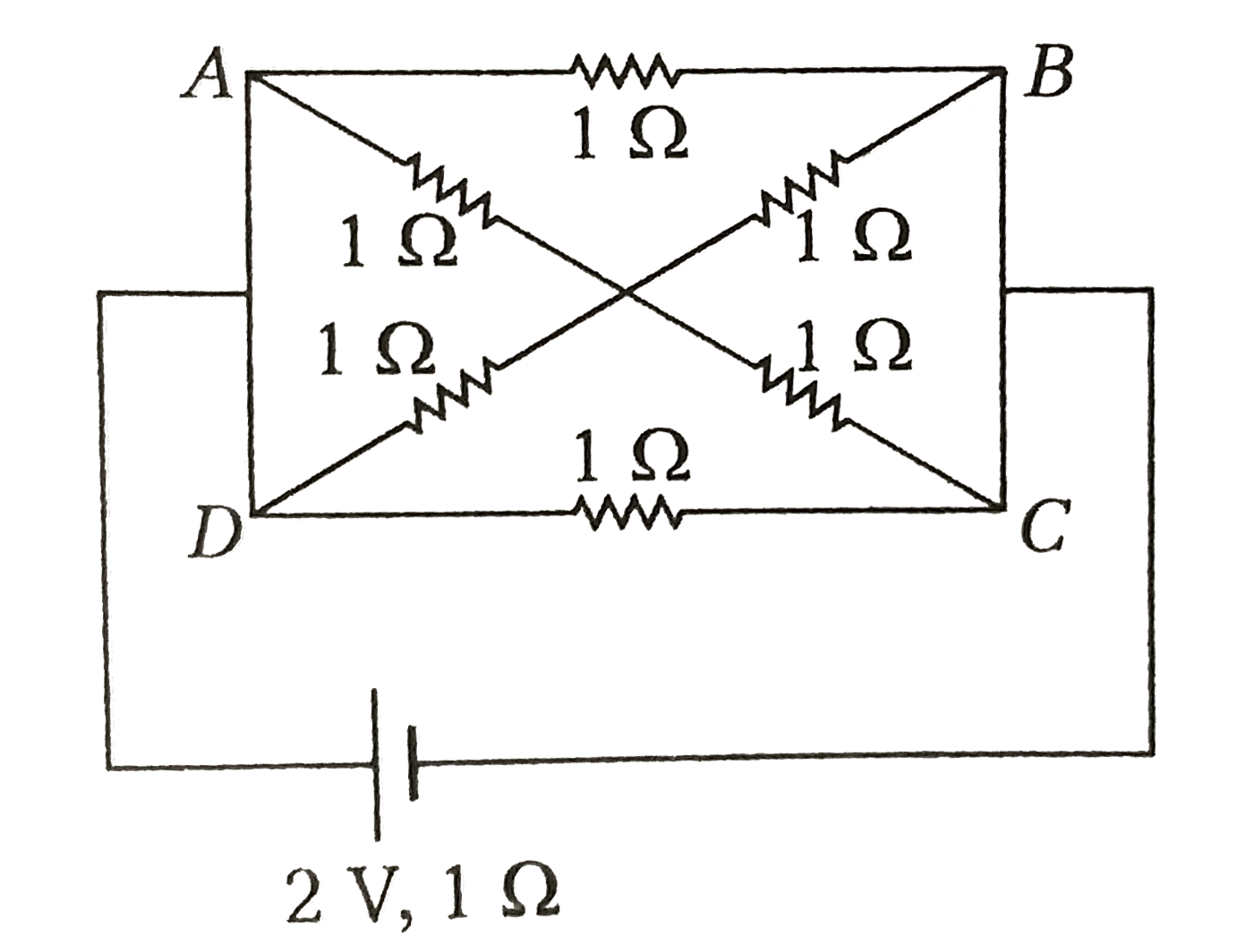
View SolutionIn the circuit shown in figure
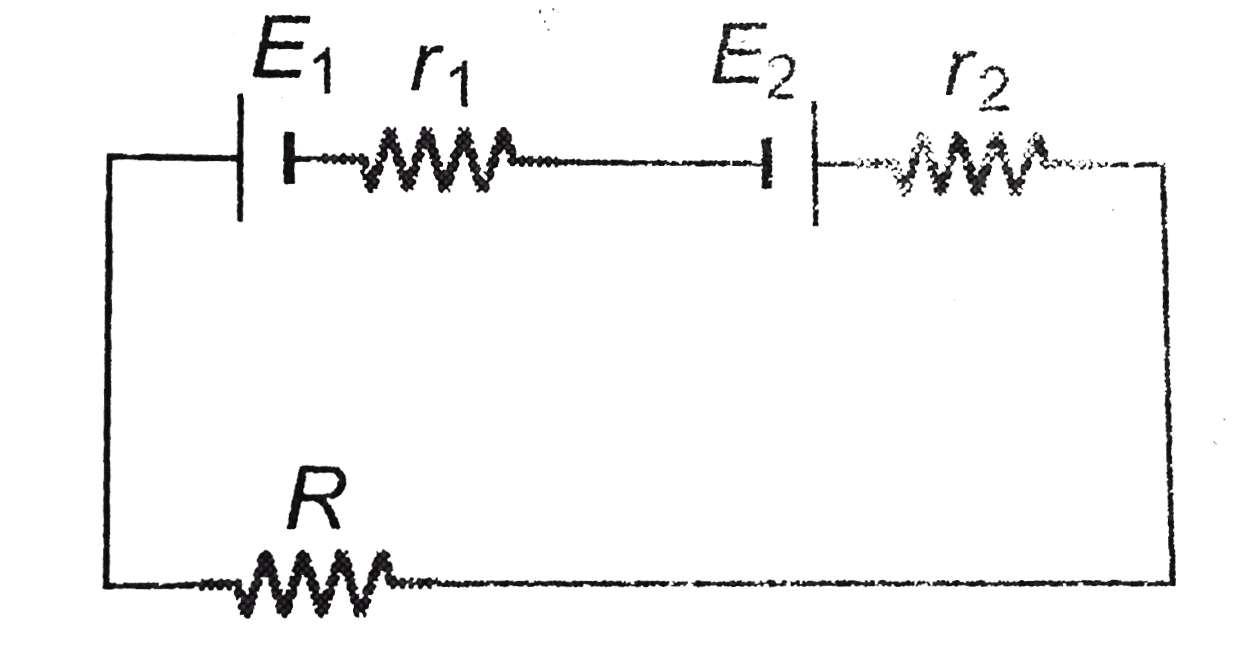
`E_1=10 V, E_2=4V, r_1=r_2=1Omega` and `R=2Omega`.
Find the potential difference across battery 1 and battery 2.
View SolutionFind the emf and internal resistance of a single battery which is equivalent to a combination of three batteries as show in figure.
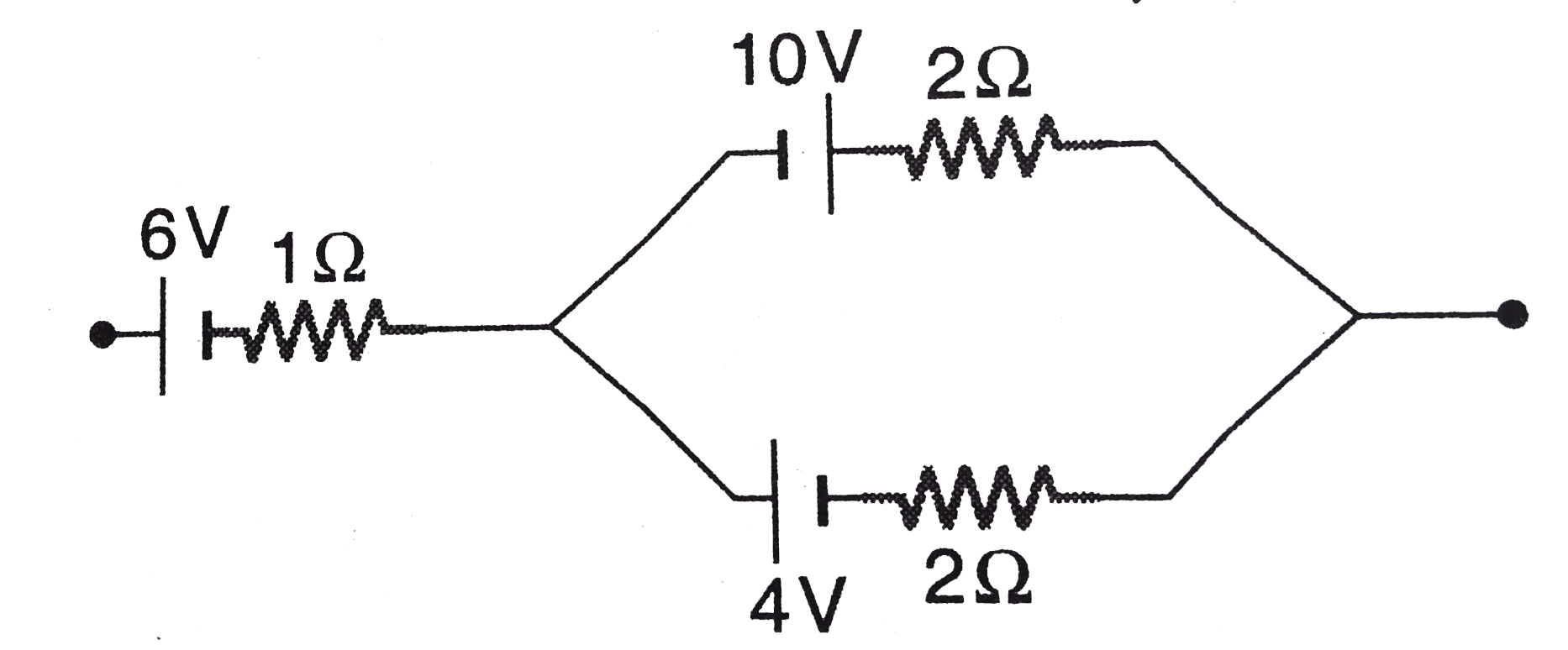
View SolutionTwo identical cells of emf 1.5 V each joined in paralllel provide supply to an external circuit consisting of two resistances of `7 Omega` each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
View SolutionFind the minimum number of cell required to produce an electron current of `1.5A` through a resistance of `30 Omega` .Given that the emf internal resistance of each cell are `1.5 V` and `1.0 Omega` respectively
View Solution36 cells each of internal resistance `0.5 Omega` and emf 1.5 V each are used to send current through an external circuit of `2 Omega` resistance. Find the best mode of grouping them and the current through the external circuit.
View Solution12 cells, each of emf `1.5` V and internal resistance of `0.5Omega`, are arranged in m rows each containing n cells connected in series, as shown. Calculate the values of n and m for which this combination would send maximum current through an external resistance of `1.5 Omega`.

View SolutionFind currents in different branches of the electric circuit shown in figure.
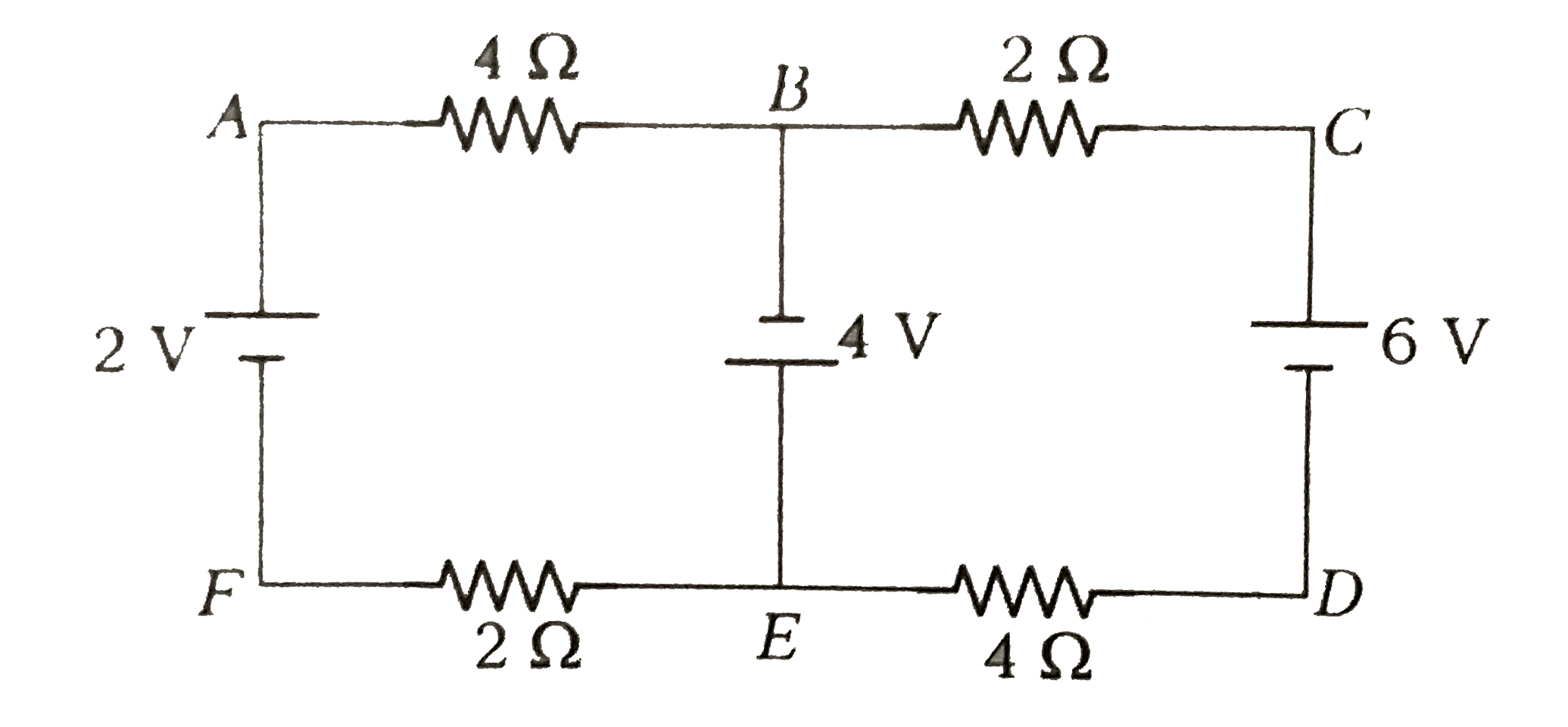
View SolutionIn example above, find the potential difference between points F and C.
View Solution(i) Find the potential difference between A and B.

View SolutionIn the circuit shown in figure find the heat developed across each resistance in `2 s`.
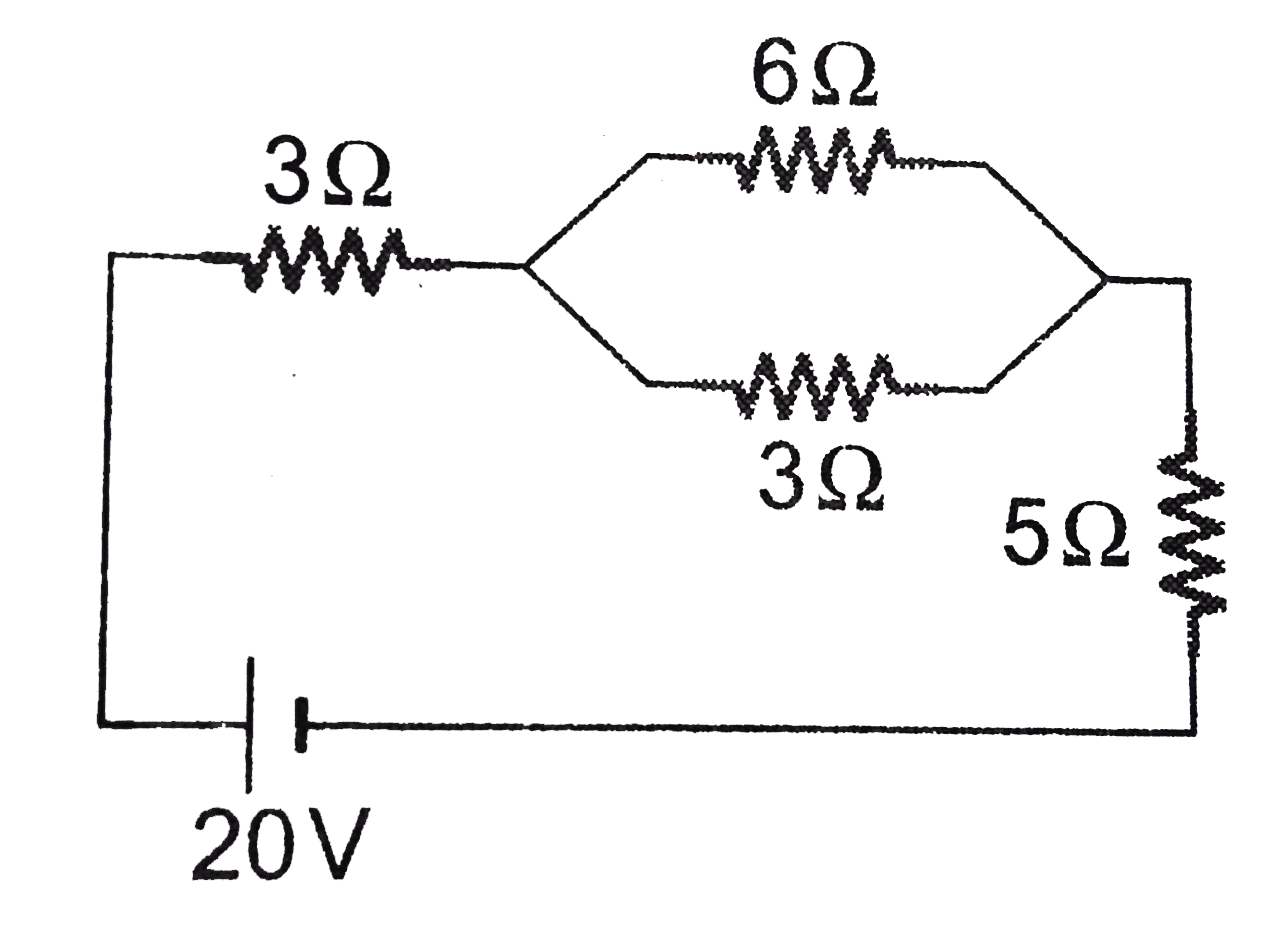
View SolutionIn the circuit shown in the following figure, find
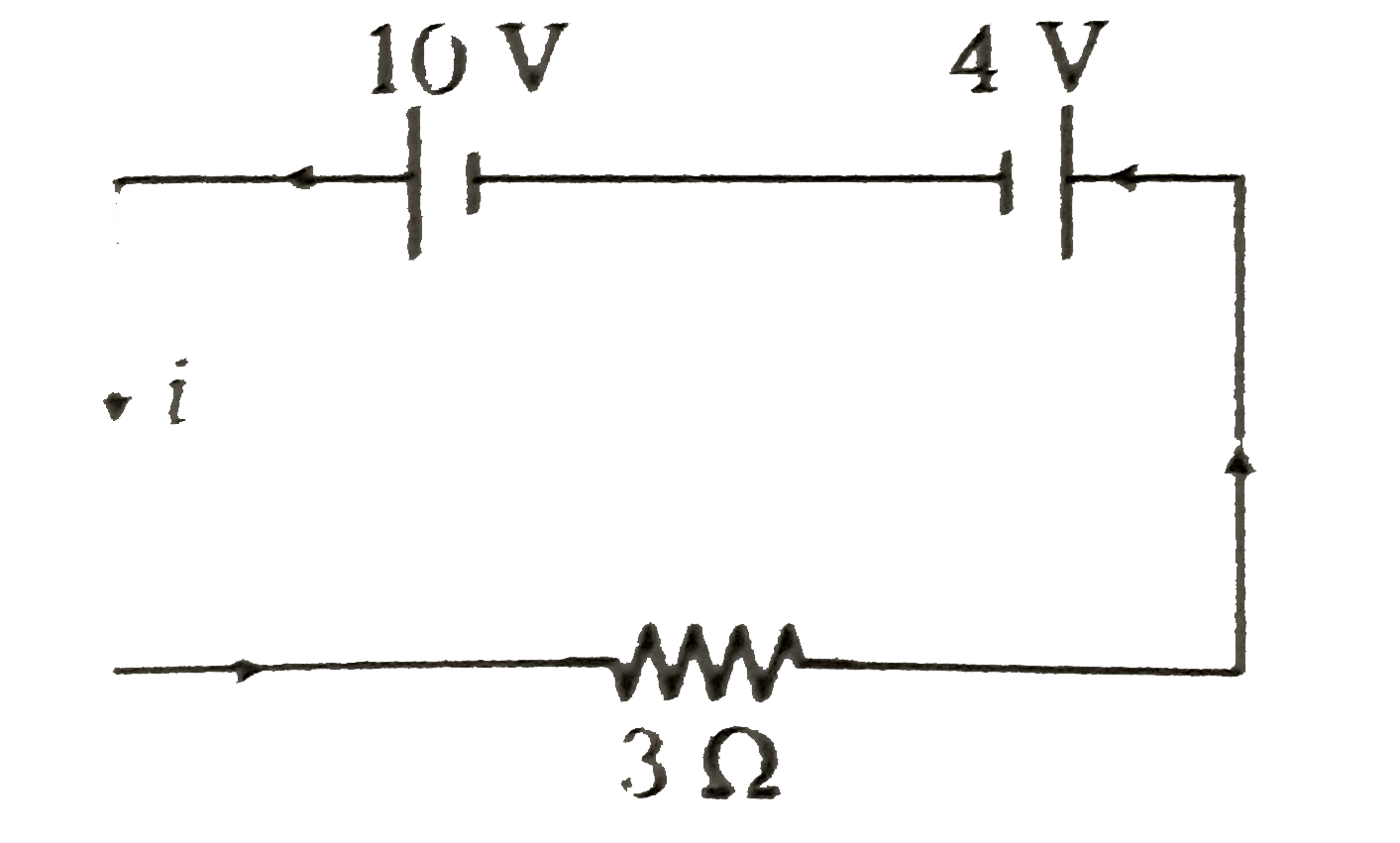
View SolutionIn the following figures, each of the three resistances, the rating of 24 W and resistance of `6Omega`. Find the maximum power rating of the circuit.
View SolutionTwo bulbs having rating of 60 W, 220 V and 100 W, 220 V are joined (i) in series, (ii) in parallel. Which of the two will glow brighter in each case?
View SolutionA series circuit consists of three bulbs connected to a battery as shown. When switch `S` is closed, what happens to (a) Power consumed in bulb `X` and `Y` (b) Power consumed in bulb `Z` (c ) the current in the circuit (d) the voltage drop across three bulbs and (e) the power consumed in circuit?

View SolutionWhat shunt resistance is required to make the `1.00 mA`, `20 Omega` Galvanometer into an ammeter with a range of 0 to `50.0A`?
View SolutionHow can we make a galvanometer with `G=20 Omega` and `i_g=1.0 mA` into a voltmeter with a maximum range of `10 V`?
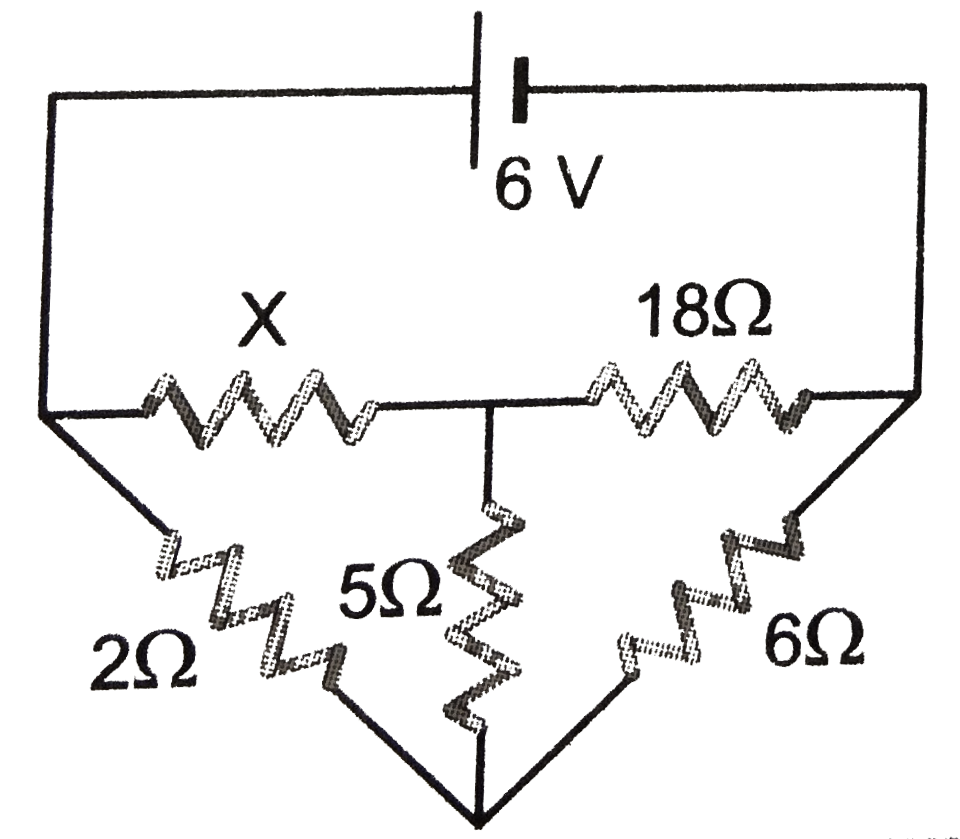
View SolutionFind out the magnitude of resistance X in the circuit shown in figure, When no current flows through the `5 Omega` resistance
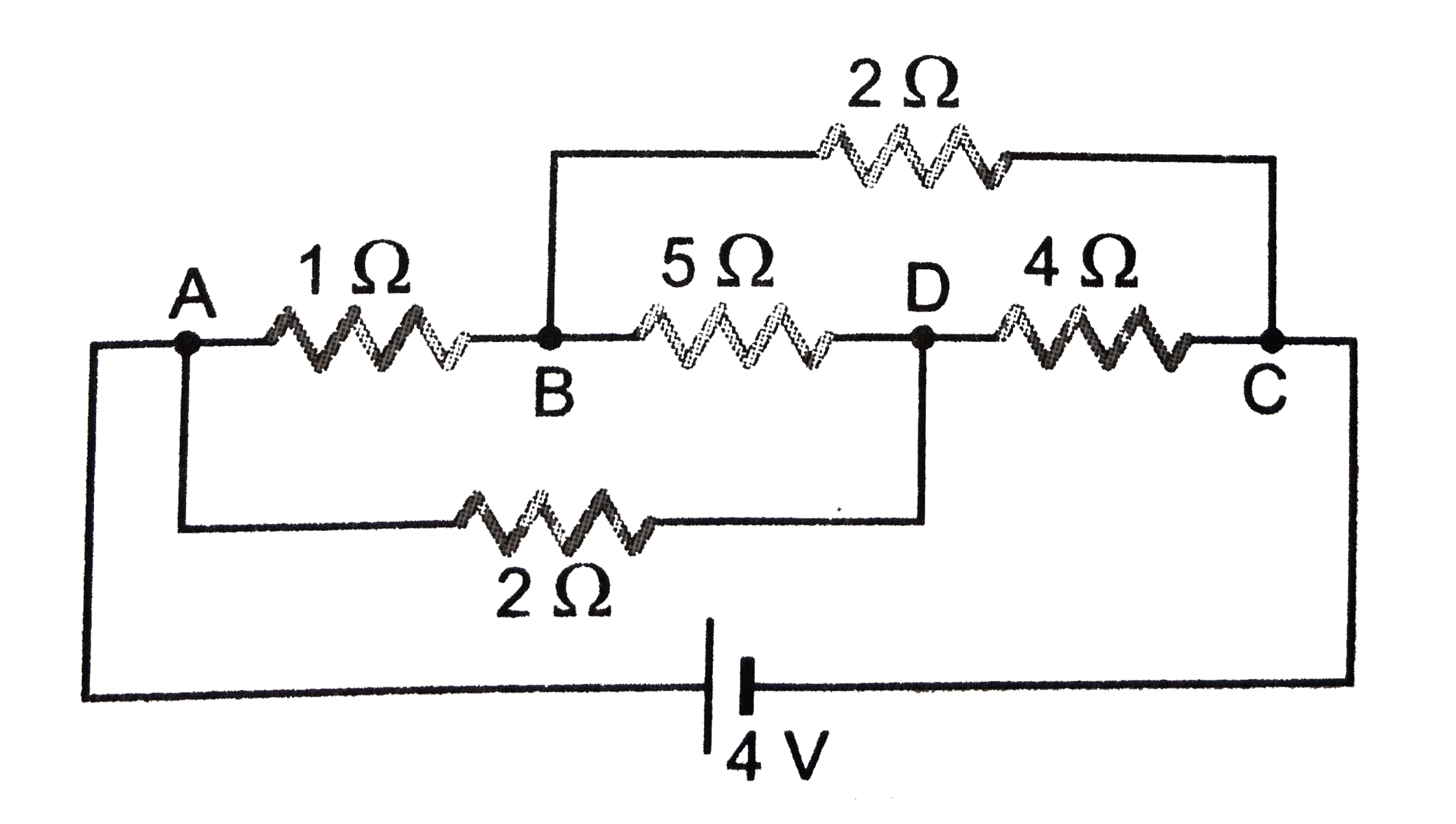
View SolutionCalculate the current the current drawn from the battery by the network of resistors shown in figure.
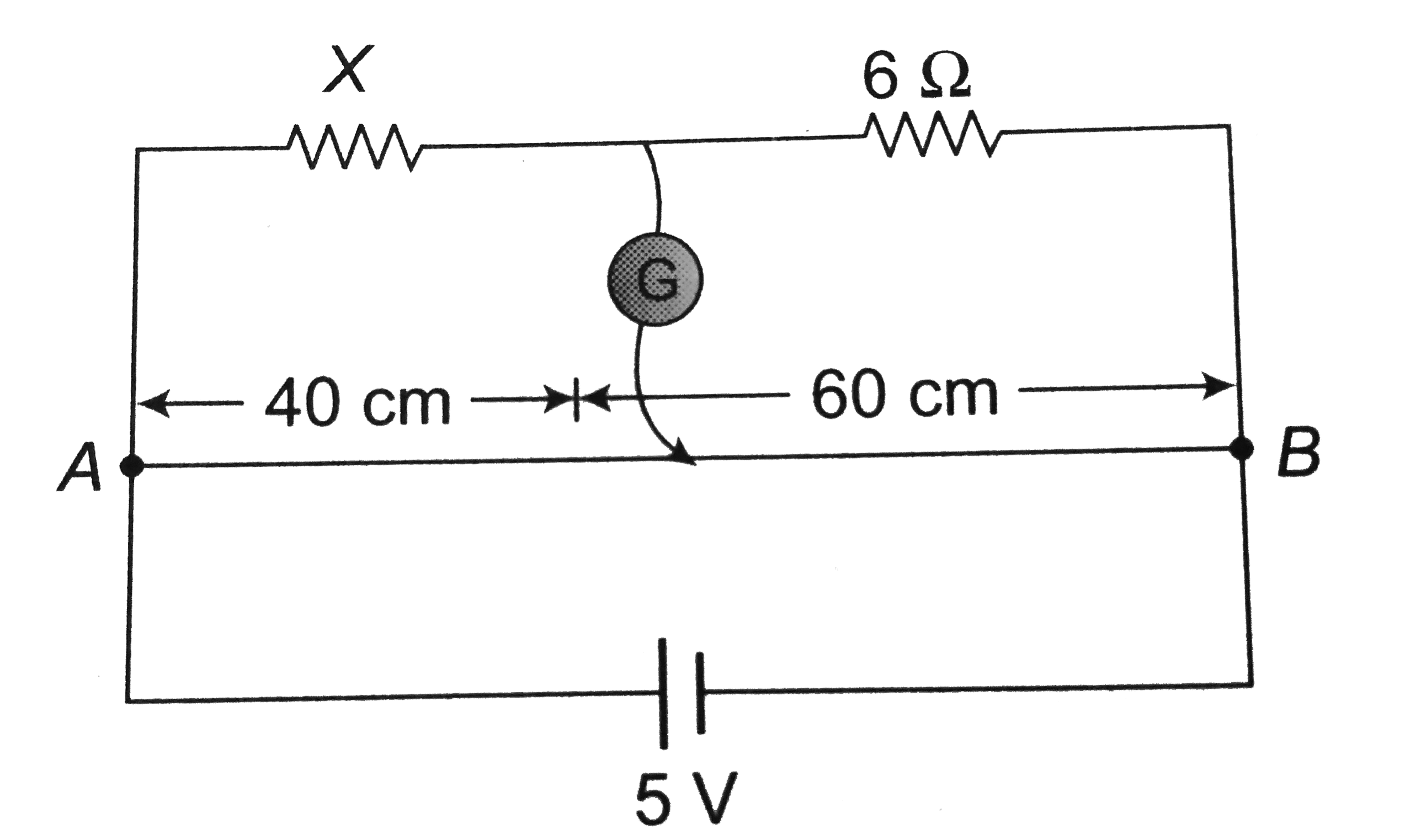
View SolutionIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance `.1 ohm//cm`. The value of unknown resistance `X` and the current drawn from the battery of negligible resistance is
View SolutionThe figure
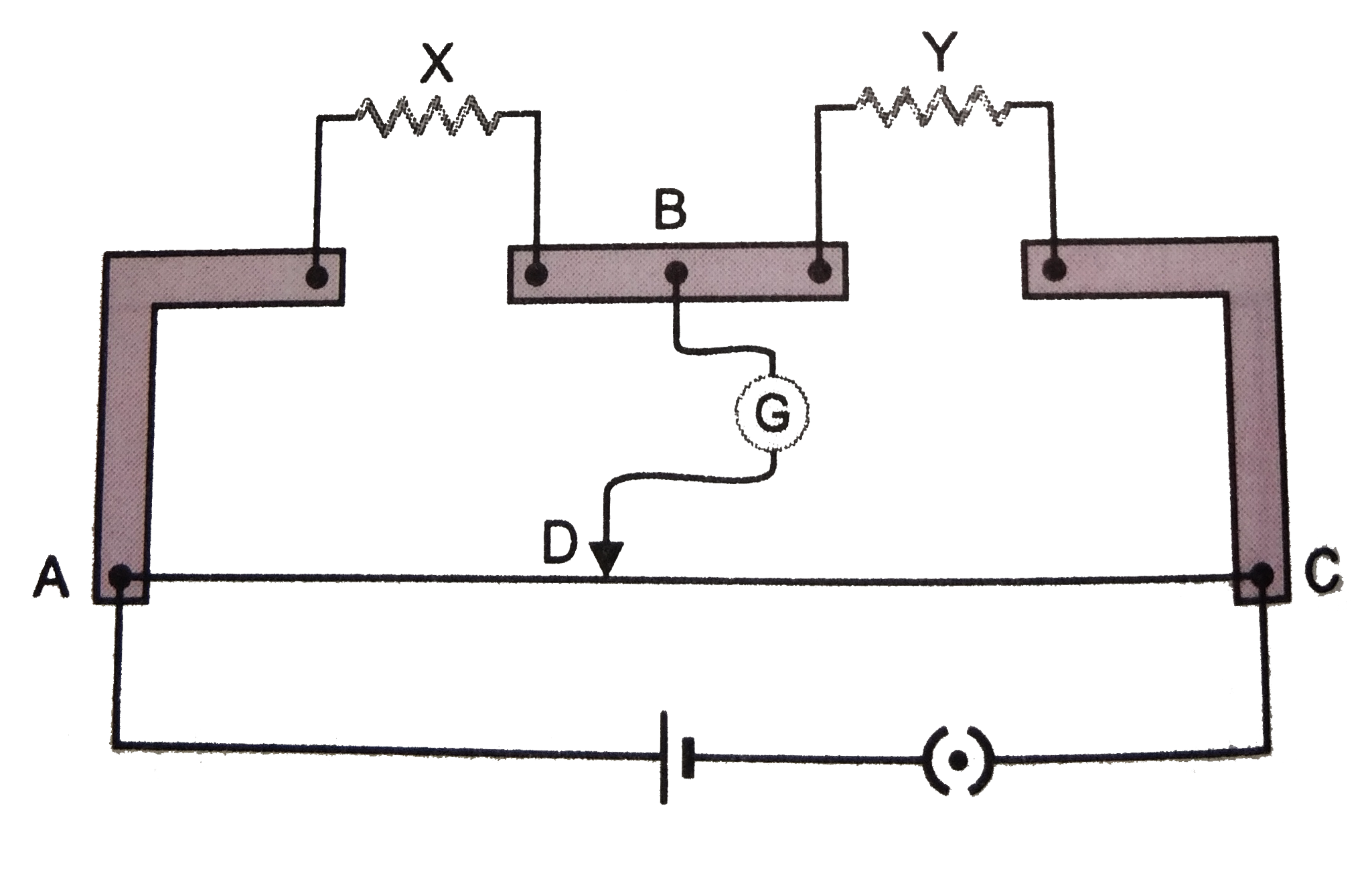
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of `15 Omega` is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of `30 Omega` were connected in parallel with Y.
View SolutionA potentiometer wire is 10 m long and has a resistance of `18Omega`. It is connected to a battery of emf 5 V and internal resistance `2Omega`. Calculate the potential gradient along the wire.
View SolutionA cell can be balanced against `110 cm` and `100 cm` of potentiometer wire, respectively with and without being short circuited through a resistance of `10 Omega`. Its internal resistance is
View SolutionIn a potentiometer arrangement, a cell of emf `2.25V` gives a balance point at `30.0` cm length of the wire. If the cell is replaced by another cell and the balance point shifts to `60.0` cm, then what is the emf of the second cell?
View SolutionA potentiometer wire of length `100 cm` having a resistance of `10 Omega` is connected in series with a resistance `R` and a cell of emf `2V` of negligible internal resistance. A source of emf

of `10 mV` is balanced against a length of `40 cm` of the potentiometer wire. What is the value of resistance `R` ?
View SolutionAB is `1` meter long uniform wire of `10 Omega` resistance. Other data are shown in the diagram. Calculate (i) potential gradient along `AB` (ii) length `AO` when galvanometer shown deflection
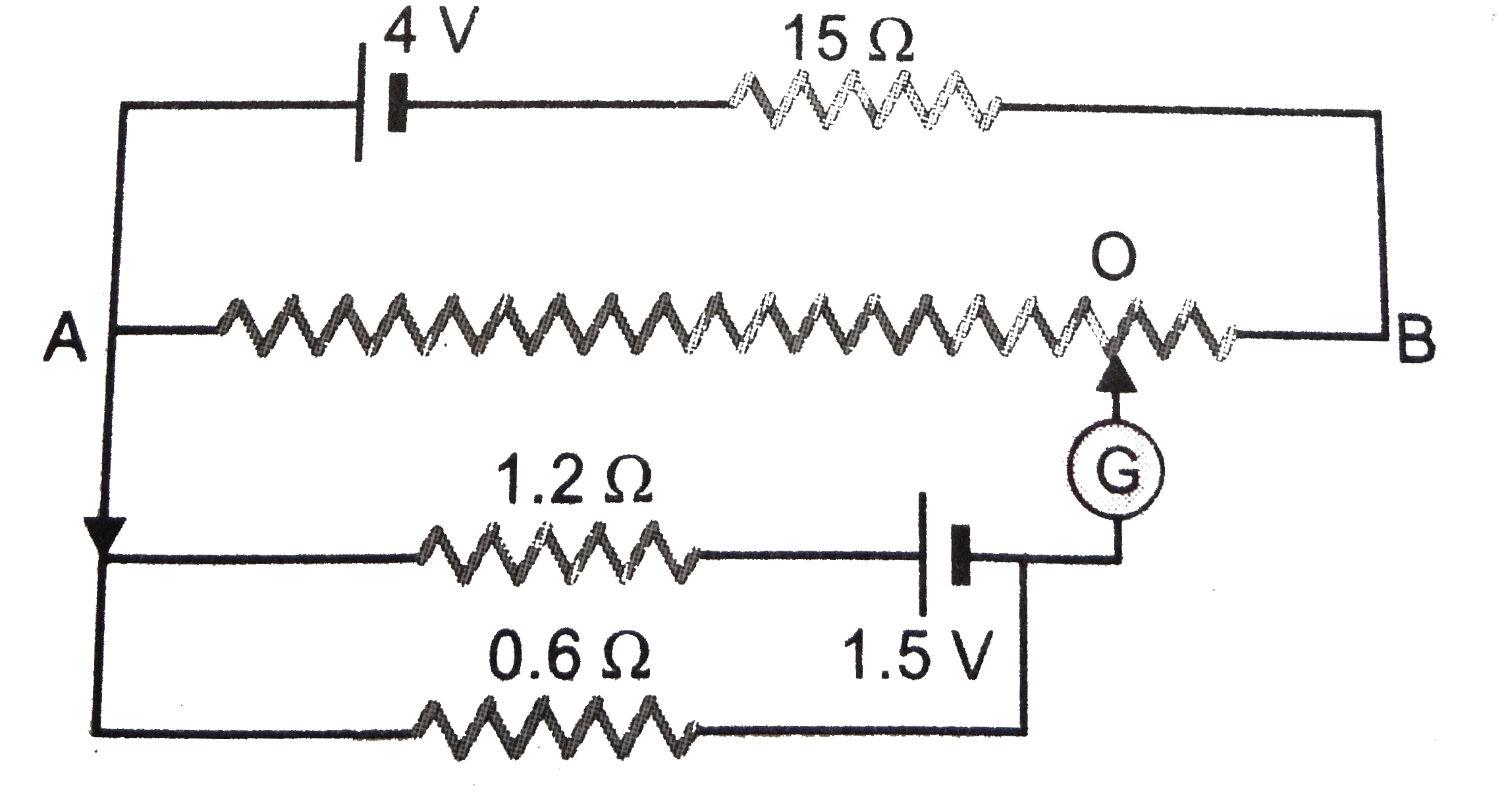
View Solution
Example questions and complete solutions for chapter CURRENT ELECTRICITY of DC PANDEY PHYSICS (HINGLISH) of Class 12
All Exercises from DC PANDEY NEET Class 12 PHYSICS CURRENT ELECTRICITY
- B. Assertion and reason
- Check point
- Example
- Example Example Type
- Example Type 1
- Example Type 2
- Example Type 3
- Example Type 4
- Example Type 5
- Example Type 6
- Exercise 23.1
- Exercise 23.10
- Exercise 23.11
- Exercise 23.12
- Exercise 23.13
- Exercise 23.2
- Exercise 23.3
- Exercise 23.4
- Exercise 23.5
- Exercise 23.6
- Exercise 23.7
- Exercise 23.8
- Exercise 23.9
- Level 1 Assertion And Reason
- Level 1 Objective
- Level 1 Subjective
- Level 2 Comprehension Example Type
- Level 2 More Than One Correct
- Level 2 Single Correct
- Level 2 Subjective
- Match the columns
- Medical entrances gallery
- Miscellaneous Examples
- OBJECTIVE_TYPE
- Taking it together