Complete Solutions to EXERCISE -1 of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| DISHA PUBLICATION | EXERCISE -1 |
| Number Of Questions | 60 |
| Academic Year | 2023-24 |
In planetary motion the areal velocity of possition vector of a planet depends of angular velocity `(omega)` and the distance of the planet from sun (r). If so the correct relation for areal velocity is
View SolutionA planet goes round the sun three times as fast as the earth. If `r_(p) and r_(e)` are the radii of orbit of the planet and the earth respectively then
View SolutionThe time period of a satellite of earth is 5 hours. If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become
View SolutionThe maximum and minimum distance of a comet form the sun are `8xx10^(12)m and 1.6xx10^(12)m`. If its velocity when nearest to the sun is `60m//s`, what will be its velocity in m/s when it is farthest
View SolutionThe period of moon's rotation around the earth is approx. 29 days. IF moon's mass were 2 fold its present value and all other things remain unchanged, the period of Moon's rotation would be nearly
View SolutionA planet of mass `m` moves around the Sun of mass Min an elliptical orbit. The maximum and minimum distance of the planet from the Sun are `r_(1)` and `r_(2)`, respectively. Find the relation between the time period of the planet in terms of `r_(1)` and `r_(2)`.
View SolutionA satellite moves round the earth in a circular orbit of radius R making one revolution per day. A second satellite moving in a circular orbit, moves round the earth once in 8 days. The radius of the orbit of the second satellite is
View SolutionFigure shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If `t_1 and t_2` be the time taken by the planet to go from a to b and from c to d respectively
View SolutionA planet moves around the sun. at a given point `P`, it is closest from the sun at a distance `d_(1)`, and has a speed `V_(1)`. At another point `Q`, when it is farthest from the sun at a distance `d_(2)`, its speed will be
View SolutionFigure showns a planet in an elliptical orbit around the sun S. Where is the kinetic energy of the planet maximum?

View SolutionThe distance of two planets from the sun are `10^(13) and 10^(12)` m respectively. The ratio of the periods of the planet is
View SolutionA satellite is revolving round the earth in an orbit of radius r with time period T. If the satellite is revolving round the earth in an orbit of radius `r + Deltar(Deltar lt lt r)` with time period `T + DeltaT(DeltaT lt lt T)` then.
View SolutionTwo satellites revolve round the earth with orbital radii 4R and 16 R, if the time period of first satellite is T then that of the other is
View SolutionA comet moves in an elliptical orbit with an eccentricity of e = 0.20 around a star. The distance between the perihelion and the aphelion is `1.0 xx 10^(8)` km. If the speed of the comet at perihelion is 81 km/s, then speed of the comet at the aphelion is :
View SolutionTwo masses `m_(1)` and `m_(2) (m_(1) lt m_(2))` are released from rest from a finite distance. They start under their mutual gravitational attraction
View SolutionTwo bodies of masses 4 kg and 9 kg are separated by a distance of 60 cm. A 1 kg mass is placed in between these two masses. If the net force on 1 kg is zero, then its distance from 4 kg mass is
View SolutionA body weighs 72 N on the surface of the earth. What is the gravitational force on it due to earth at a height equal to half the radius of the earth from the surface
View SolutionIf masses of two point objects is doubled and distance between them is tripled, then gravitational force of attraction between then will nearly
View SolutionThe distance of the centres of moon the earth is D. The mass of earth is 81 times the mass of the moon. At what distance from the centre of the earth, the gravitational force on a particle will be zero.
View SolutionTwo concentric uniform shells of mass `M_(1) and M_(2)` are as shown in the figure. A particle of mass m is located just within the shell `M_(2)` on its inner surface. Gravitation force on 'm' due to `M_(1)` and `M_(2)` will be
` (##DSH_NTA_JEE_MN_PHY_C07_E02_020_Q01.png" width="80%">
View SolutionTwo stars of mass `m_(1)` and `m_(2)` are parts of a binary star system. The radii of their orbits are `r_(1)` and `r_(2)` respectivey, measured from the centre of mass of the system. The magnitude of gravitational force `m_(1)` exerts on `m_(2)` is
View SolutionThe percentage change in the acceleration of the earth towards the Sun from a total eclipse of the Sun to the point where the Moon is on a side of earth directly opposite to the Sun is
View SolutionThere are two bodies of masses `10^(3)` kg and `10^(5)` kg separated by a distance of 1 km. At what distance from the smaller body, the inensity of gravitational field will be zero
View SolutionTwo sphere of masses `m` and `M` are situated in air and the gravitational force between them is `F`. The space around the masses in now filled with a liquid of specific gravity `3`. The gravitational force will now be
View SolutionAs we go from the equator to the poles, the value of `g`
View SolutionThe ratio between the values of acceleration due to gravity at a height `1 //km` above and at a depth of 1 km below the Earth’s surface is (radius of Earth is R)
View SolutionThe angular velocity of the earth with which it has to rotate so that the acceleration due to gravity on `60^@` latitude becomes zero is
View SolutionIn order to make the effective acceleration due to gravity at the equator to zero, the numerical value of the angular velocity of rotation of the earth should be
[Radius of the earth=6400 km, `g=10m/s^(2)`]
View SolutionWhat should be the velocity of earth due to rotation about its own axis so that the weight at equator become 3/5 of initial value. Radius of earth on equator is 6400 km
View SolutionIf the density of a small planet is the same as that of earth while the radius of the planet is `0.2` times that of the earth the gravitational on the surface of that planet is :
View SolutionThe weight of an object in the coal mine, sea level and at the top of the mountain are `W_(1),W_(2)` and `W_(3)` respectively, then
View SolutionThe radius of a planet is n times the radius of earth (R). A satellite revolves around it in a circle of radius 4nR with angular velocity `omega`. The acceleration due to gravity on planet's surface is
View SolutionHow many hours would make a day if the earth were rotating at such a high speed that the weight of a body on the equator were zero
View SolutionLet g be the acceleration due to gravity at the earth's surface and K the rotational kinetic energy of the earth. Suppose the earth's radius decreases by 2%. Keeping all other quantities constant, then
View SolutionLet `omega` be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth `d` below earth's surface at a pole `(dlt ltR)`. the value of `d` is-
View SolutionIf earth is supposed to be a sphere of radius R , if `g_(30)` is value of acceleration due to gravity at latitude of `30^(@)` and g at the equator, the value of `g-g_(30^(@))` is
View SolutionA(nonrotating) star collaps onto from an initial radius `R_(i)` with its mass remaining unchanged. Which curve in figure best gives the gravitational acceleration `a_(g)` on the surface of the star as a function of the radius of the star during the collapse?
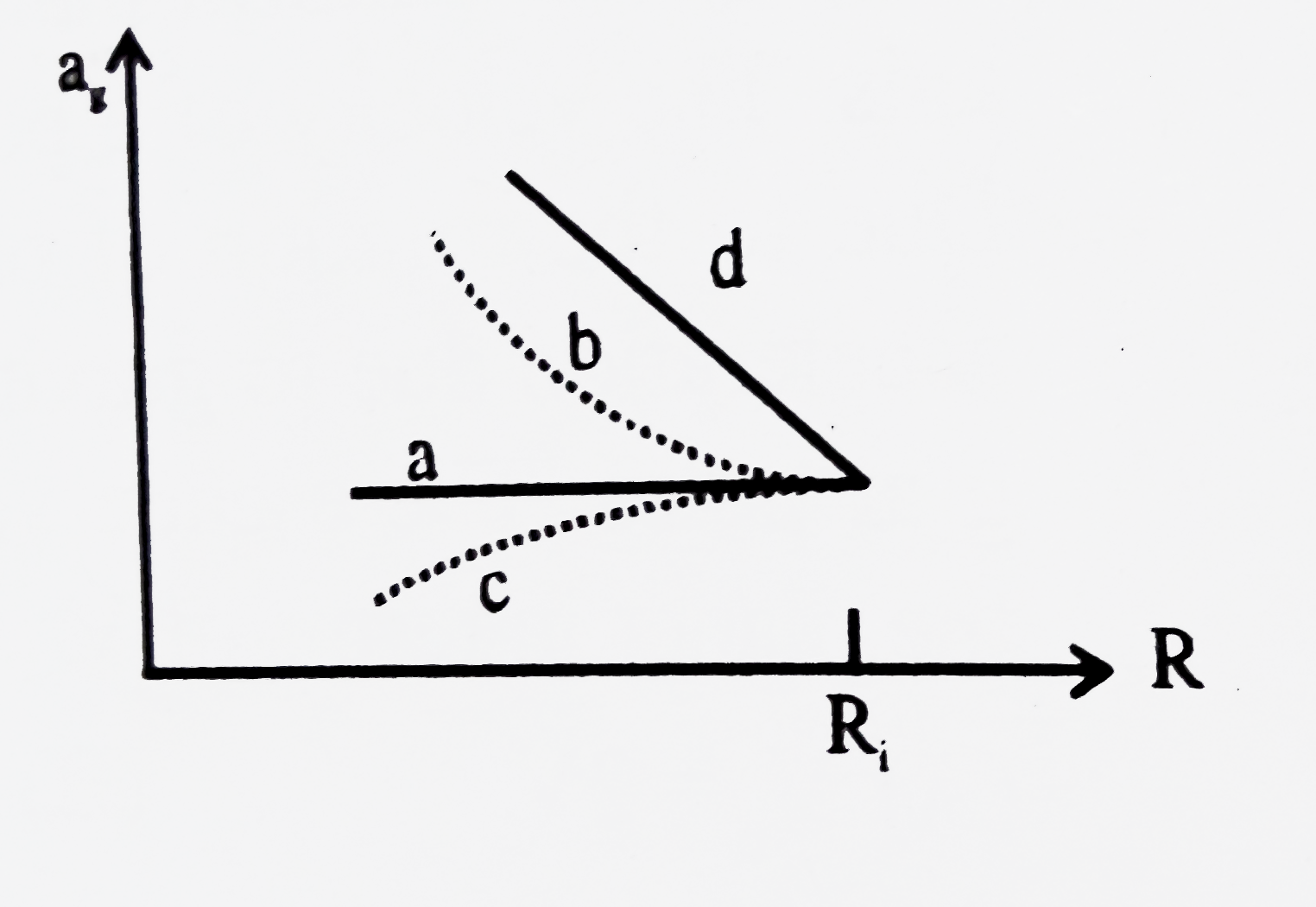
View SolutionIf the mass of earth is eighty times the mass of a planet and diameter of the planet is one fourth that of earth, then acceleration due to gravity on the planet would be
View SolutionA research satellite of mass `200 kg` circles the earth in an orbit of average radius `3 R//2`, where `R` is the radius of the earth. Assuming the gravitational pull on the mass of `1 kg` on the earth's surface to be `10 N`, the pull on the satellite will be
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is `r_(2) - r_(1)`
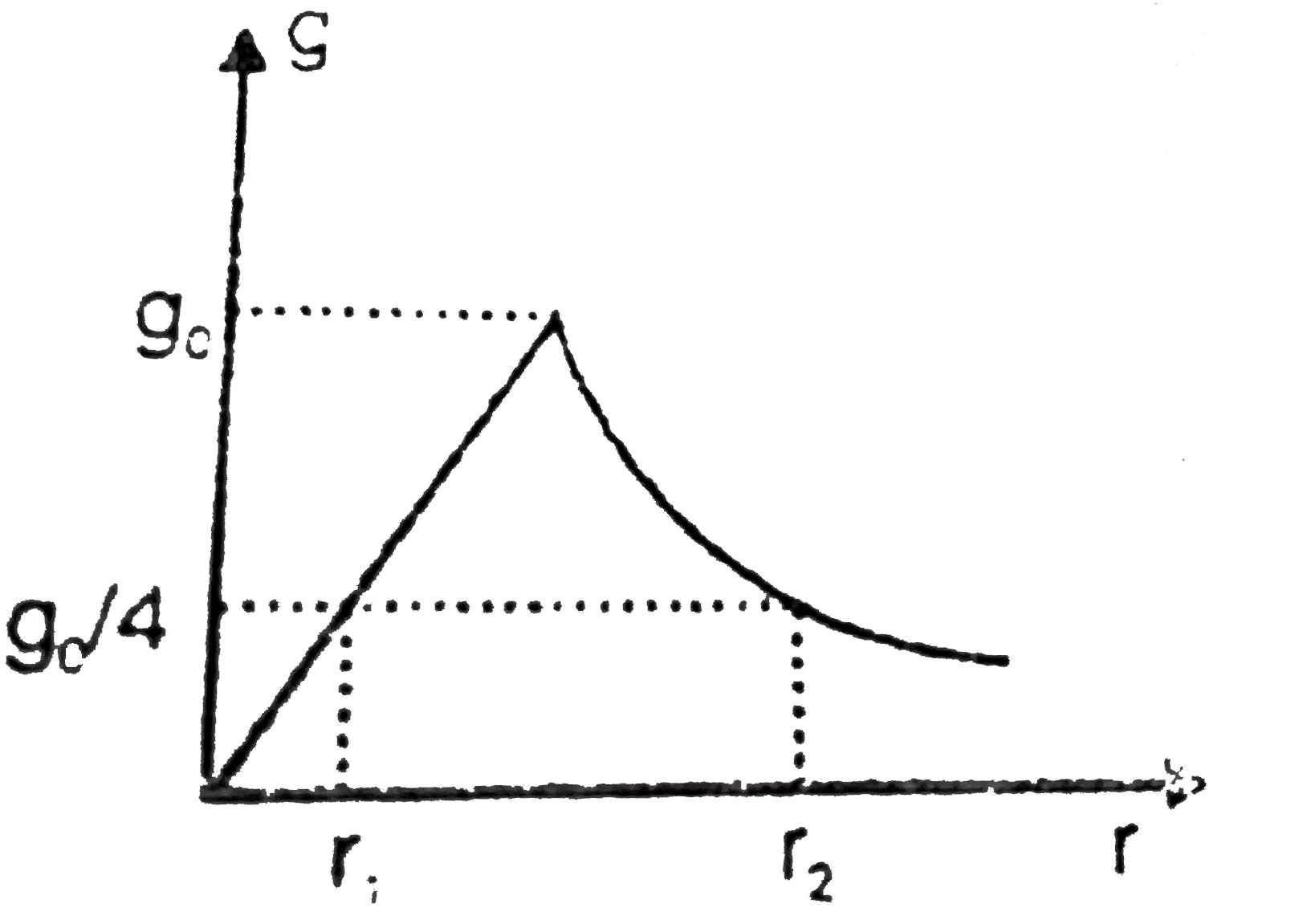
View SolutionThe acceleration due to gravity on the planet `A` is `9` times the acceleration due to gravity on planet `B`. A man jumps to a height of `2m` on the surface of `A`. What is the height of jump by the same person on the planet `B`?
View SolutionA roller coaster is designed such that riders experience "weightlessness" as they go round the top of a hill whose radius of curvature is `20m`. The speed of the car at the top of the hill is between
View SolutionIn a certain region of space gravitational field is given by `I = - (k//r)`. Taking the reference point to be at `r = r_(0)`, with gravitational potential `V = V_(0)`, find the gravitational potential at distance `r`.
View SolutionGravitational field intensity at the centre of the semi circle formed by a thin wire `AB` of mass `m` and length `L` is
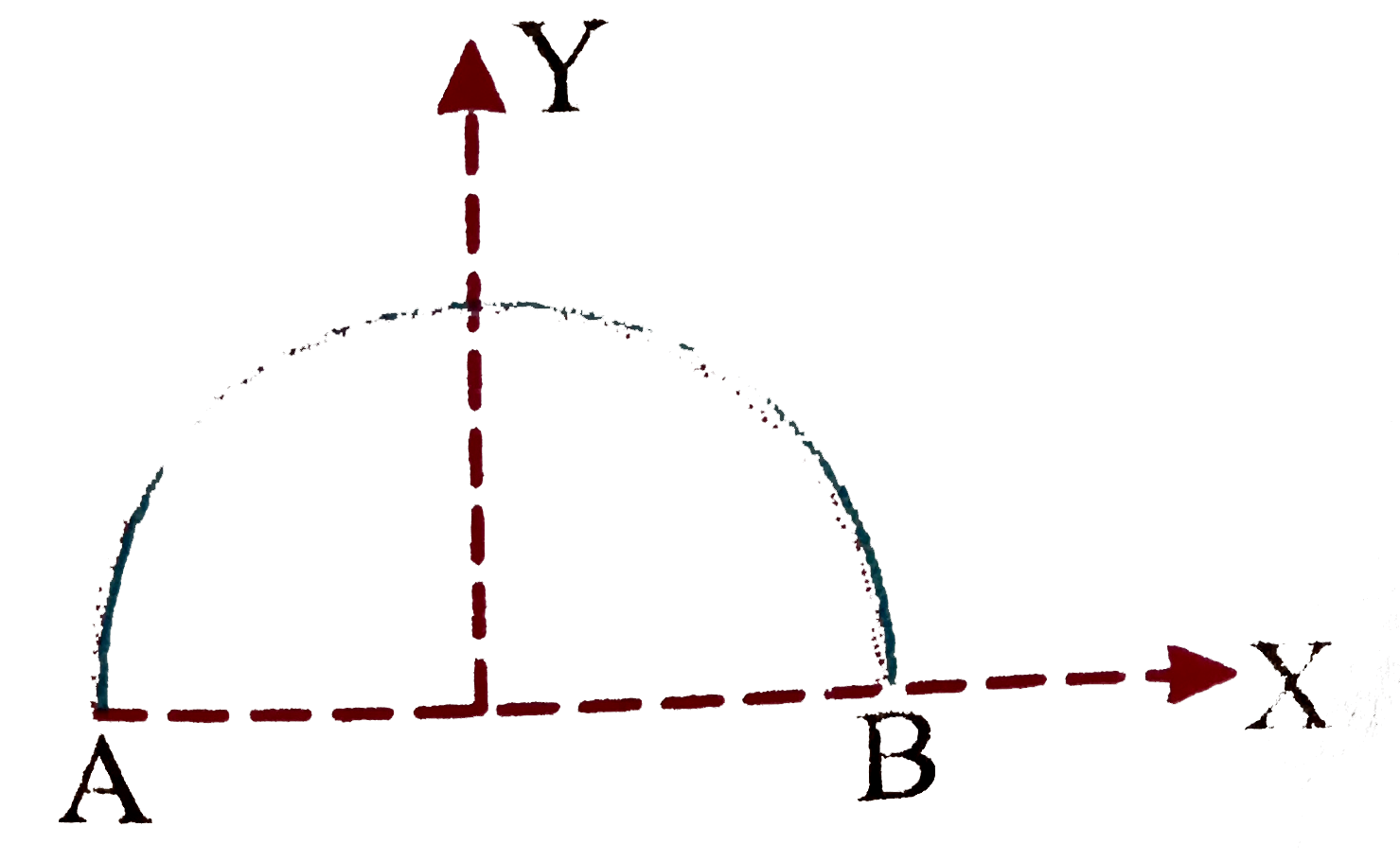
View SolutionA planet is moving in an elliptic orbit. If `T,V,E` and `L` stand, respectively, for its kinetic energy, gravitational potential energy, total energy and angular momentum about the centre of force, then
View SolutionIf g is the acceleration due to gravity on the earth's surface, the gain in the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth, is
View SolutionThe magnitude of gravitational potential energy of the moon earth system is U with zero potential energy at infinite separation. The kinetic energy of the moon with respect to the earth is K.
View SolutionThe gravitational potential due to earth at infinite distance from it is zero. Let the gravitational potential at a point `P` be `-5 J kg^(-1)`. Suppose, we arbitrarily assume the gravitational potential at infinity to be `+10 J kg^(-1)`, then the gravitational potential at `P` will be
View SolutionTwo rings having masses `M` and `2M` respectively, having the same radius are placed coaxially as shown in the figure.
 If the mass distribution on both the rings is non-uniform, then the gravitational potential at point `P` is
If the mass distribution on both the rings is non-uniform, then the gravitational potential at point `P` is
View SolutionThe escape velocity of an object projected from the surface of a given planet is independent of
View SolutionThe mean radius of earth is R, its angular speed on its own axis is w and the acceleration due to gravity at earth's surface is g. What will be the radius of the orbit of a geostationary satellite
View SolutionThe moon has a mass of `(1)/(81)` that of the earth and radius of `(1)/(4)` that of the earth. The escape speed from the surface of the earth is 11.2 km`//`s. The escape speed from surface of the moon is-
View SolutionA planet in a distant solar systyem is 10 times more massive than the earth and its radius is 10 times smaller. Given that the escape velocity from the earth is `11kms^(-1)`, the escape velocity from the surface of the planet would be
View SolutionWhat is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 3R ?
View SolutionTwo particles of equal mass `'m'` go around a circle of radius `R` under the action of their mutual gravitaitonal attraction. The speed of each particle with respect to their centre of a mass is -
View SolutionThe earth is assumed to be a sphere of raduis `R`. A plateform is arranged at a height `R` from the surface of the `fv_(e)`, where `v_(e)` is its escape velocity form the surface of the earth. The value of `f` is
View SolutionThree equal masses (each m) are placed at the corners of an equilateral triangle of side `a`. Then the escape velocity of an object from the circumcentre P of triangle is
View SolutionA satellite is revolving round the earth (mass `M_(e)`) in a circular orbit of radius `a` with velocity `V_(0)` A particle of mass `m` is projected from the satellite in forward direction with relative velocity `v[sqrt((5)/(4))-1]V_(0)`. During subsequent motion of particle.
View SolutionThe orbital velocity of an artifical satellite in a circular orbit just above the earth's surface is `V_(0)`. For a satellite orbiting at an altitude of half of earth's radius, the orbital velocity is
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View Solution
EXERCISE -1 questions and complete solutions for chapter GRAVITATION of DISHA PUBLICATION PHYSICS (HINGLISH) of Class 12