Complete Solutions to EXERCISE-2 of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| DISHA PUBLICATION | EXERCISE-2 |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
Two spherical bodies of mass M and 5M & radii R & 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smallar body just before collision is
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance `sqrt3` a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is

View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is `R`, the radius of the planet would be
View SolutionA point `P` lies on the axis of a fixed ring of mass `M` and radius `a`, at a distance `a` from its centre `C`. A small particle starts from `P` and reaches `C` under gravitational attraction only. Its speed at `C` will be.
View SolutionTwo bodies of masses m and M are placed at distance d apart. The gravitational potential (V) at the position where the gravitational field due to them is zero V is
View SolutionA spherical uniform planet is rotating about its axis. The velocity of a point on its equator is `V`. Due to the rotation of planet about its axis the acceleration due to gravity `g` at equator is `1//2` of `g` at poles. The escape velocity of a particle on the planet in terms of `V`.
View SolutionThe gravitational field, due to the 'left over part' of a uniform sphere (from which a part as shown , has been 'removed out') at a very far off point, P , located as shown, would be (nearly) :
` (##DSH_NTA_JEE_MN_PHY_C07_E03_008_Q01.png" width="80%">
View SolutionThe change in the value of acceleration of earth toward sun, when the moon coomes from the position of solar eclipse to the position on the other side of earth in line with sun is :
(mass of moon `=7.36xx10^(22)` kg, orbital radius of moon `=3.8xx10^(8)` m.)
View Solutionfind the gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length L and mass m, placed such that r is the distance between the centre of the sphere and the near end of the road.
View SolutionTwo bodies of mass `m_(1) and m_(2)` are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attaction. Show that their relative velocity of approach at separation r betweeen them is
`v=sqrt(2G(m_(1)+m_(2)))/(r)`
View SolutionTwo identical thin ring each of radius `R` are co-axially placed at a distance `R`. If the ring have a uniform mass distribution and each has mass `m_(1)` and `m_(2)` respectively, then the work done in moving a mass `m` from the centre of one ring to that of the other is :
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is `r_(min)`. The farthest distance from the sun is `r_(max)` if the orbital angular velocity of the planet when it is nearest to the Sun `omega` then the orbital angular velocity at the point when it i at the farthest distanec from the sun is
View SolutionThe radii of two planets are respectively `R_(1) and R_(2)` and their densities are respectively `rho_(1) and rho_(2)`.The ratio of the accelerations due to gravity at their surface is
View SolutionTwo blocks A and B of masses `M_(A)` and `M_(B)` respectively, are located 1.0 m apart on a horizontal surface. The coefficient of static friction `mu_(s)` between the block and the surface is 0.50. Block A is secured to the surface and cannot move, What is the minimum mass of Block A that provides enough gravitation attraction to move Block B ? Th universal gravitation constant is 6.67`xx 10^(-11) Nm^(2)/kg^(2)` .
View SolutionA cavity of radius `R//2` is made inside a solid sphere of radius `R`. The centre of the cavity is located at a distance `R//2` from the centre of the sphere. The gravitational force on a particle of a mass `'m'` at a distance `R//2` from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here `g=GM//R^(2)`, where `M` is the mass of the solide sphere]
View SolutionA planet of radius R has an acceleration due to gravity of `g_(s)` on its surface. A deep smooth tunne is dug on this planet, radially inward, to reach a point P located at a distance of `(R)/(2)` from the centre of the planet. Assume that the planet has uniform density. The kinetic energy required to be given to a small body of mass m, projected radially outward from P, so that it gains a maximum altitude equal to the thrice the radius of the planet from its surface, is equal to
` (##DSH_NTA_JEE_MN_PHY_C07_E03_017_Q01.png" width="80%">
View SolutionFour point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
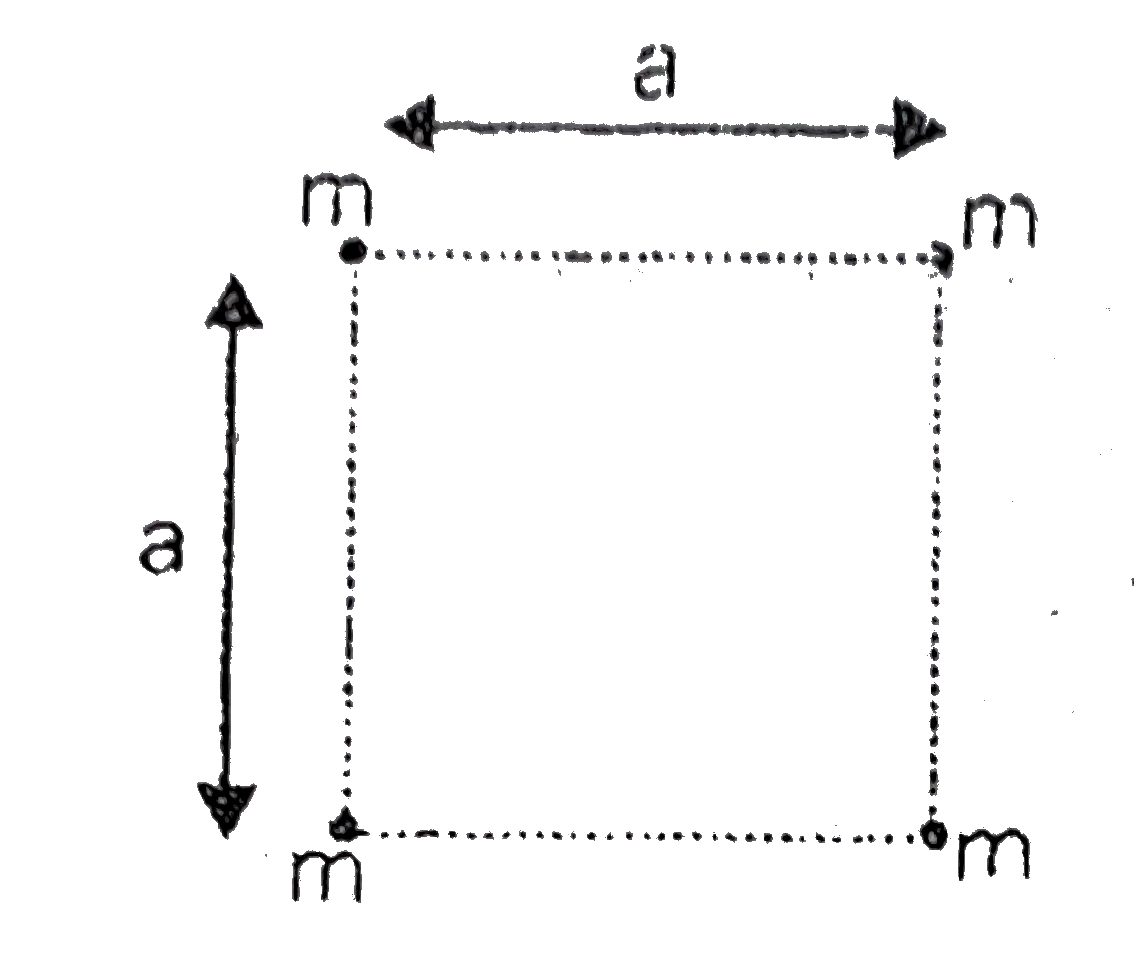 .
.
View SolutionIn order to simulate different values of `g` aspiring astronauts are put on a plane which dives in a parabola given by the equation `x^2 = 500y`. Where `x` is horizontal, `y` is vertically upwards, both being measured in meter. The `x`-component of the velocity of the plane is constant throughout, and has the value of `360 km//h`. the effective `g`("g-force") experienced by an astronaut on the plane equals
View SolutionTwo spheres each of mass M are situated at distance 2d (see figure). A particle of mass m (m `lt lt `M) is taken along the path shown in figure. The work done in the process from A to B is
` (##DSH_NTA_JEE_MN_PHY_C07_E03_020_Q01.png" width="80%">
View SolutionTwo hypothetical planets of masses `m_(1) and m_(2)` are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is 'd' ?
(speed of `m_(1) ` is `v_(1)` and that of `m_(2)` is `v_(2)`)
` (##DSH_NTA_JEE_MN_PHY_C07_E03_021_Q01.png" width="80%">
View SolutionThe gravitational potential of two homogeneous spherical shells `A` and `B` of same surface density at their respective centres are in the ratio `3:4`. If the two shells collapse into a single one such that surface charge density remains the same, then the ratio of potential at an internal point of the new shell to shell `A` is equal to
View SolutionA skylab of mass `m` kg is first launched from the surface of the earth in a circular orbit of radius `2R` (from the centre of the earth) and then it is shifted from this circular orbit to another circular orbit of radius `3R`. The minimum energy required to place the lab in the first orbit and to shift the lab from first orbit to the second orbit are
View SolutionWith what minimum speed should `m` be projected from point `C` in presence of two fixed masses `M` each at `A` and `B` as shows in the figure such that mass `m` should escape the gravitational attraction of `A` and `B` ?
View SolutionA spherical hollow cavity is made in a lead sphere of radius `R` such that is surface touches the outside surface of the lead sphere and passes through its centre. The mass of the sphere before hollowing was `M` with what gravitational force will the hollowed out lead sphere attract a small sphere of mass m which lies at a distacne d from the centre of the lead sphere on the straight line connecting the centeres of the spheres and that of the hollow if `d =2R`
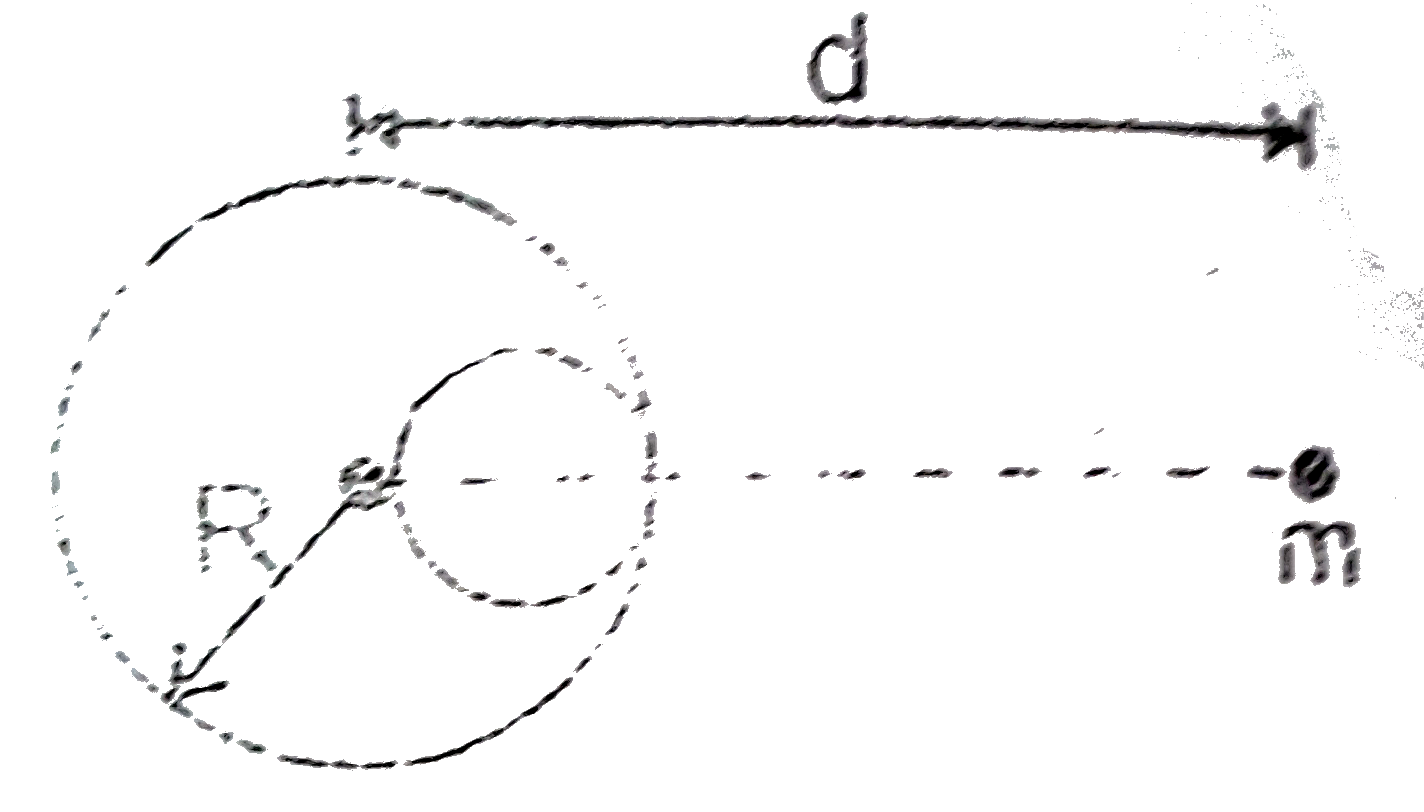 .
.
View SolutionA body starts from rest from a point distant `r_(0)` from the centre of the earth. It reaches the surface of the earth whose radius is `R`. The velocity acquired by the body is
View SolutionA solid sphere of uniform density and radius `R` applies a gravitational force of attraction equal to `F_(1)` on a particle placed at `P`, distance `2R` from the centre `O` of the sphere. A spherical cavity of radius `R//2` is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force `F_(2)` on same particle placed at `P`. The radio `F_(2)//F_(1)` will be
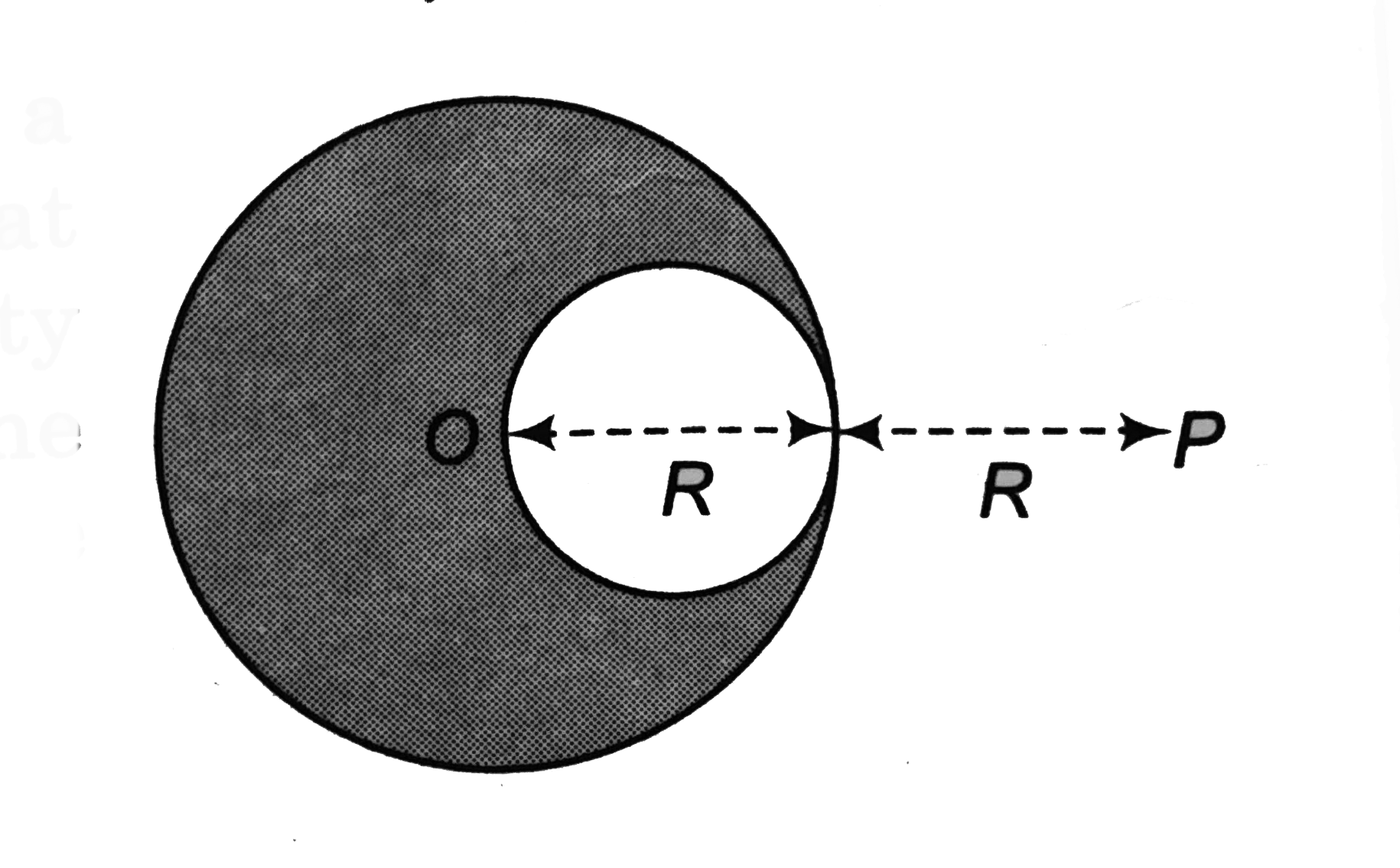
View SolutionA small satellite of mass m is revolving around earth in a circular orbit of radius `r_(0)` with speed `v_(0)` . At certain point of its orbit, the direction of motion of satellite is suddenly changed by angle `theta = cos^(-1) `(3/5) by turning its velocity vector , such that speed remains constant. The satellite consequently goes to elliptical orbit around earth. the ratio of speed at perigee to speed at apogee is
View SolutionA solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
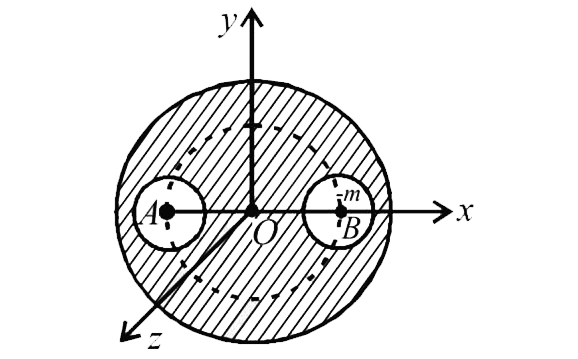
View SolutionAn artificial satellite (mass m) of a planet (mass M) revolves in a circular orbit whose radius is n times the radius R of the planet in the process of motion the satellite experiences a slight resistance due to cosmic dust. Assuming the force of resistance on satellite to depend on velocity as `F=av^(2)` where 'a' is a constant caculate how long the satellite will stay in the space before it falls on to the planet's surface.
View Solution
EXERCISE-2 questions and complete solutions for chapter GRAVITATION of DISHA PUBLICATION PHYSICS (HINGLISH) of Class 12