Complete Solutions to JEE Advanced of chapter त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी |
| ERRORLESS HINDI | JEE Advanced |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
`0 lt theta lt (pi)/(2)` के लिए `underset( m =1)overset(6)(Sigma) cosec ( theta + ((m-1)pi)/(4 )) cosec (theta + (mpi)/( 4)) = 4 sqrt(2) ` का के हल निम्न है।
View Solution`theta = 0 ` तथा `theta= pi//2` के मध्य स्थित `theta` के वह मान जो समीकरण
`|{:(1 + sin^(2) theta , cos^(2) theta , 4 sin 4 theta ),(sin^(2) theta , 1 + cos^(2) theta , 4 sin 4 theta ),( sin^(2) theta , cos^(2) theta , 1 + 4 sin theta):}|=0` को संतुष्ट करते है
View Solutionनियत आधार BC वाले त्रिभुज ABC का शीर्ष बिन्दु A इस प्रकार गतिमान है। कि cos B + cos C =4 `sin^(2) .(A)/(2 )`यदि `a,b` एवं c क्रमश त्रिभुज के कोणों A,B तथा C की सम्मुख भुजाओं की लम्बाईयों प्रदिर्शित करते है। तब
View Solutionयदि त्रिभुज ABC के कोण A का आंतरिक द्विभाजक AD, भुजा BC से बिंदु D पर मिले तो दिखाइए कि `AB gt BD`
View Solutionएक त्रिभुज में दो बडी भुजाऐं है जिनकी लम्बाइयो क्रमश 10 तथा 9 है यदि त्रिभुज के कोण समान्तर श्रेणी मे हो तब तीसरी भुजा की लम्बाईयो होगी।
View Solutionएक त्रिभुज ABC के आस्तित्व में होने के लिए निम्न में से कौन से प्रतिबंध सन्तुष्ट होगें
View Solutionत्रिभुज PQR में P वृहत्म कोण है। तथा `cos P = (1)/(3)` । इसके अतिरिक्त त्रिभुज का अन्तवृत भुजाओं PQ,QR तथा RP को क्रमश N,L तथा M पर इस तरह स्पर्श करता है। कि PN, QL तथा RM की लम्बाईयाँ क्रमागत सम पूर्ण संख्याएं है तब त्रिभुज की भुजा की सम्भावित लम्बाई है।
View Solutionयदि `cos x = sqrt(1 – sin 2x ) , 0 lt x lt pi` तब x का मान है।
View Solutionयदि `0 le x le 2 pi`तथा`|cos x | le sin x `तब
View Solutionयदि `T_(n) =sin^(n ) theta+ cos^(n ) theta , (T_(6)-T_(4))/(T_(6))`.=m तब m के मान के लिए संतुष्ट होता है।
View Solutionयदि `tan alpha` तथा`tan beta` समीकरण `x^(2) +px + q=0` के मूल है जबकि `p ne 0 ,q ne 1` तब
View Solutionयदि `sin alpha`तथा `cos alpha` के बीच गुणोत्तर माध्य cos 2`beta` है। तब cos 4 'beta' बराबर है :
View Solutionमाना ABCD एक समान्तर चतुर्भज है जो एक वृत के अन्दर बनाया गया है। निम्न में से कौन कथन हमेशा सही है।
View Solutionनिम्न में से कौन सा कथन हमेशा सही है (जहाँ Q परिमेय संख्याओं के समुच्चय को निरूपित करता है। )
View Solution`alpha = pi //7 `के लिए कौन सा कथन सही है।
View Solutionनिम्न में से कौन सा सही है।
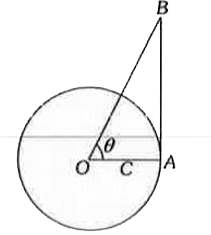
View Solutionएक वृत केन्द्र`O ` पर केन्दित है जिसकी त्रिज्या 1 तथा बिन्दु A है। बिन्दु A पर रेखाखण्ड AB वृत पर स्पर्श रेखा है। तथा `/_AOB=theta` यदि बिन्दु C, OA पर स्थित है तथा रेखा BC कोण ABO को समदभातिज करती हैं तो OC बराबर है।
View Solution`(a+2) sin alpha + (2a+1) cos alpha =(2a + 1) ` यदि `tan alpha` है।
View Solutionयदि `b gt 1 , sin t gt 0 ,cos t gt 0` तथा `log_(b ) (sin t ) =x ` तब `log_(b ) (cos t )` बराबर है।
View Solutionयदि `cos x + cos y =a, cos 2 x + cos 2y =b` और `cos 3x + cos 3y =c` निम्न में से कौन सा कथन सत्य है।
View Solutionनिम्न में से कौन सा कथन सही है।
View Solutionसमीकरण `3^(sin 2x + 2cos^(2) x) + 3^(1-sin 2x + 2sin^(2)x =28, x` के मान के लिए संतुष्ट होता हैं जो के द्वारा दिया गया है।
View Solution`theta =0` तथा `theta= ( pi)/(2)` के बीच `theta` का मान जो समीकरण
`|{:(1 + cos^(2) theta , sin^(2) theta , 4 sin 4 theta ),(cos^(2) theta , 1 + sin^(2) theta , 4 sin 4 theta ),( cos^(2) theta , sin^(2) theta , 1 + 4 sin 4 theta):}|=0` को संतुष्ट करता है।
View Solutionनिकाय के समीकरणों `2^(sin x+cos y = 1,16^(sin^(2) x+ cos^(2) y =4` का हल है।
View Solutionअन्तराल `(-pi ,pi)` में x के मान जो समीकरण `8^(1+|cosx|+|cos^(2)x|+|cos^(3) x|+,,,`अंनत तक `=4^(3)` को संतुष्ट करते है।
View Solution[x] महत्तम पुर्णाक को दर्शाता है। [x] `leq x ` है। तब समीकरण sin x= [1+sin x ]+[1-cos x] के किस किस अंतराल में कोई नही हल नही है।
View Solution`/_A` को कोणीय समदिबाहु AD है। AD के लम्बवत DE ,AC को E पर प्रतिच्छेद करता हैं और F तक बढाने पर AB पर मिलता है तब
View Solution`Delta ABC` के लिये निम्न में से कौन सा सही है।
View Solutionएक व्यक्ति मैदान पर खडे होकर प्रक्षण करता है। कि मीनार के शिखर का उन्नयन कोण `30^(@)` है एक निश्चित दिशा में वह दूरी a तय करके पता चलता हैं कि मीनार के शिखर का उन्नयन कोण दूरी तय करता है। और पाता है। कि शिखर का उन्नयन कोण पहले का दुगुना हो गया है मीनार की उँचाई है।
View Solutionमाना कि `s= {X in (-pi ,pi) : X =ne0 +-(pi)/(2)}` है समुच्चय S से समीरण् `sqrt(3) sec x+ cosec x+ 2(tan x –cotx) =0` के सभी स भिन्न हलो का योग है।
View Solutionमाना कि त्रिभुज xyz में कोणों x,y,z के समाने की भुजाओं की लम्बाई क्रमश `x,y,z` है और 2s =x+y+z है यदि `(s-x)/(4) = (s-y)/(3 ) = (s-z)/(2)` और त्रिभुज XYZ के अतवृत का क्षेत्र फल `(8 pi)/(3)` है तब
View Solutionमान कि `alpha` एवं `beta` इस प्रकार की अशून्य वाव्तविक संख्याये है कि `2(cos beta - cos alpha) + cos alpha cos beta =1` तब निम्न में से कौन सा से सत्य है।
View Solutionएक त्रिभुज PQR मे माना कि `/_PQR = 30^(@)` और भुजाये PQ और QR की लम्बाई क्रमश `10sqrt(3)` और 10 है तब निम्नलिखित में से कौनसा कथन सत्य है।
View Solutionअसमिका `2 ^(sin theta) + 2 ^(cos theta) ge 2^(1-(1)/(sqrt(2))) theta` के सभी वास्तविक मानो के लिए सत्य है।
View Solutionयदि एक त्रिभुज के कोणीय बिंदुओं से विपरीत भुजाओ पर लंब`p_(1),p_(2) ,p_(3)` हो तो
कथन -1 `(1)/(p_(1) ) + (1)/(p_(2) ) + (1)/(p_(3)) = (1)/(r )`
कथन -2 एक त्रिभुज में `(s)/( Delta ) = (1)/(r )`
View Solutionकथन-1 यदि A क्षेत्र फल है तथा त्रिभुज की तीनो भुजाऐ योग 2s है तब A `lt (s^(2))/( 3 sqrt(3))`
कथन-2 A.M `le G.M`
View Solutionकथन -1 ,वृत भुजा a वाले समबाहु त्रिभुज के अन्दर व वृत में किसी भी अन्त वर्ग का क्षेत्र फल `(a^(2))/(6)` है।
कथन-2 अन्त वृत की त्रिजया `r= (Delta )/(s ) ` है।
View Solutionएक मीनार AB ऊर्ध्वाधर से पश्चिम की दिशा में `alpha` कोण से झुकी है। A बिन्दु से d दूरी पर पूर्व की दिशा में बिन्दु C से मीनार के उच्चतम बिन्दु B का उन्नयन कोण `beta` है यदि C के पूर्व में इससे 2d दूरी पर स्थित बिन्दु D से B का उन्नयन कोण `gamma` हो तो 2 tan `alpha` का मान निम्न प्रकार से दिया गया है। जा सकता है।
View Solutionसमीकरण `(1)/(sin (pi)/(n )) = (1)/(sin ((2pi)/(n )))+ (1)/(sin ((3pi)/(n )))` को संतुष्ट करने वाले धनात्मक प्रर्णाक n` gt 3` का मान निम्न है।
View Solution`0 lt theta lt pi`को सन्तुष्ट करने वाले `theta` के सभी संभावित मानो की संख्या जिनके लिये समीकरणों के निकाय `(y+z) cos 3 theta = (xyz) sin 3theta`
`x sin 3theta =(2 cos 3 theta)/( y ) + (2 sin 3 theta)/( z)`
`(xyz ) sin 3theta = (y+2z) cos 3 theta + y sin 3theta ` का एक हल `(x_(0) ,y_(0) ,z_(0))` है जहाँ `y_(0) z_(0) ne 0` है।
View Solutionअन्तराल `(-(pi)/(2) ,(pi)/(2))` में स्थित `theta` के उन मानो की संख्या जिनके लिए `theta ne (n pi)/( 5 ) , n =0 +- 1,+-2`तथा `tan theta = cot 5 theta` एवं `sin 2theta = cos 4theta ` है।
View Solutionदिया है कि किसी त्रिभुज `ABC` के शीर्षी A,B एवं C की सम्मुख भुजाओं की लम्बाइये क्रमश `a,b` एवं c है माना कि `a=6,b=10` तथा त्रिभुज का क्षेत्र फल `15 sqrt(3) ` है यदि `/_ACB` r है तो`r^(2)` का मान है।
View Solutionअन्तराल `[0 ,2pi]` में समीकरण `(5)/(4) cos^(2) 2 x+ cos^(4) x+ sin^(4) x+ cos^(6) x+sin ^(6) x-2` के विभिन्न हलो की संख्या है।
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये

View Solution
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये

View Solution
View Solution
JEE Advanced questions and complete solutions for chapter त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी of ERRORLESS MATHS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 MATHS त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी
- Exercise
- Illustration
- JEE Advanced
- Solved Multiple Choice Question (आवती फलन )
- Solved Multiple Choice Question (ऊँचाई एवं दूरी)
- Solved Multiple Choice Question (त्रिकोणमितीय समीकरण के हल)
- Solved Multiple Choice Question (त्रिभुज की भुजाओ तथा कोणों के माध्य सम्बन्ध त्रिभुजो के हल )
- Solved Multiple Choice Question (त्रिभुजों से सम्बध्द वृत्त )