Complete Solutions to JEE ADVANCED( INTEGER TYPE) of chapter फलन, सीमा, सांतत्य तथा अवकलनीयता of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | फलन, सीमा, सांतत्य तथा अवकलनीयता |
| ERRORLESS HINDI | JEE ADVANCED( INTEGER TYPE) |
| Number Of Questions | 40 |
| Academic Year | 2023-24 |
माना एक फलन जो संबंध
`f((2tanx)/(1+tan^(2)x))=((1+cos2x)(sec^(2)x+2tanx))/2` को संतुष्ट करता है।
कथन-1 `y=f(x)` का परिसर R है।
कथन-2: रेखीय फलन का परिसर R होगा यदि प्रांत R है।
View Solutionकथन-1 `f(x)=sinx` तथा `g(x)=cosx` तत्समक फलन है।
कथन-2 दोनों फलनों के प्रांत तथा परिसर समान है।
View Solutionकथन-1 यदि `f(x)=(a^(x))/(a^(x)+sqrt(a))(agt0)` है तब
`sum_(r=1)^(2n-1)(r/(2n))=2n-1`
कथन-2: `f(x)+f(1-x)=1AAx`
View Solutionकथन-1 `x ge-1` के लिए माना `f(x)=(x+1)^(2)` है। यदि g(x) एक फलन है जिसका वक्र रेखा y=x के सापेक्ष फलन f(x) के वक्र का प्रतिबिंब है तब `g(x)=sqrt(x)-1,xge0`,
कथन-2 `g(x),f(x)` का प्रतिलोम है।
View Solutionमाना कि `f:[0,1]toR` (सभी वास्तविक संख्याओं का समुच्चय) एक फलन है। मान लीजिए फलन f दो बार अवकलनीय है `f(0)=f(1)=0` तथा `f’’(x)-2f’(x)+f(x)gee^(x),x epsilon[0,1] ` को संतुष्ट करता है।
निम्न में से कौन `0ltxlt1` के लिए सत्य है?
View Solutionमाना कि `f:[0,1]toR` (सभी वास्तविक संख्याओं का समुच्चय) एक फलन है। मान लीजिए फलन f दो बार अवकलनीय है `f(0)=f(1)=0` तथा `f"(x)-2f’(x)+f(x)gee^(x),x epsilon[0,1]` को संतुष्ट करता है।
यदि फलन `e^(-x)f(x),` अंतराल [0,1] में अपना न्यूनतम मान `x=1/4` पर लेता है तब निम्न में से कौन सत्य है?
View Solutionयदि `f(x)` एक धनात्मक वास्तविक मानों का फलन है जो x=a तथा x=b के लिए सममित है जहां a तथा b `g(x)=sqrt(1-log_(3)(x^(2)-6x+11))` के प्रांत (डोमेन) में क्रमशः न्यूनतम तथा अधिकतम मान है तब
निम्न में से कौन सा कथन सत्य है
View Solutionयदि `f(x)` एक धनात्मक वास्तविक मानों का फलन है जो x=a तथा x=b के लिए सममित है जहां a तथा b `g(x)=sqrt(1-log_(3)(x^(2)-6x+11))` के प्रांत (डोमेन) में क्रमशः न्यूनतम तथा अधिकतम मान है तब
g(x) का परिसर किस अंतराल में होगा
View Solutionयदि `f(x)` एक धनात्मक वास्तविक मानों का फलन है जो x=a तथा x=b के लिए सममित है जहां a तथा b `g(x)=sqrt(1-log_(3)(x^(2)-6x+11))` के प्रांत (डोमेन) में क्रमशः न्यूनतम तथा अधिकतम मान है तब
`S=sum_(r=1)^(50)f(r+p),prod_(r=1)^(50)f(r)=2^(50),` जहां `p=2(b-a)` तब S का न्यूनतम मान है
View Solution`x=x_(0)` पर फलन f(x) को अवकलनीय कहा जाता है यदि `Rf’(x_(0))` तथा `Lf’(x_(0))` दोनों बराबर तथा सीमित है जिनके उभयनिष्ठ मान को बिंदु `x=x_(0)` पर अवकलज या अवकलन गुणांक कहा जाता है। फलन `f(x),x=x_(0)` पर अवकलनीय नहीं है। यदि
(i) दोनों `Rf’(x_(0))` तथा `Lf’(x_(0))` का अस्तित्व है लेकिन बराबर नहीं
(ii) दोनों `Rf’(x_(0))` तथा `Lf’(x_(0))` में से कोई एक सीमित नहीं है
(iii) दोनों `Rf’(x_(0))Lf’(x_(0))` में से किसी एक का अस्तित्व नहीं है तब निम्न प्रश्नों को हल कीजिए।
यदि `f(x)="min"{x,x^(2)}` तब
View Solution`x=x_(0)` पर फलन f(x) को अवकलनीय कहा जाता है यदि `Rf’(x_(0))` तथा `Lf’(x_(0))` दोनों बराबर तथा सीमित है जिनके उभयनिष्ठ मान को बिंदु `x=x_(0)` पर अवकलज या अवकलन गुणांक कहा जाता है। फलन `f(x),x=x_(0)` पर अवकलनीय नहीं है। यदि
(i) दोनों `Rf’(x_(0))` तथा `Lf’(x_(0))` का अस्तित्व है लेकिन बराबर नहीं
(ii) दोनों `Rf’(x_(0))` तथा `Lf’(x_(0))` में से कोई एक सीमित नहीं है
(iii) दोनों `Rf’(x_(0))Lf’(x_(0))` में से किसी एक का अस्तित्व नहीं है तब निम्न प्रश्नों को हल कीजिए।
फलन `f(x)="max"{1-x),(1+x),2}AA x epsilon R` है
View Solution`x=x_(0)` पर फलन f(x) को अवकलनीय कहा जाता है यदि `Rf’(x_(0))` तथा `Lf’(x_(0))` दोनों बराबर तथा सीमित है जिनके उभयनिष्ठ मान को बिंदु `x=x_(0)` पर अवकलज या अवकलन गुणांक कहा जाता है। फलन `f(x),x=x_(0)` पर अवकलनीय नहीं है। यदि
(i) दोनों `Rf’(x_(0))` तथा `Lf’(x_(0))` का अस्तित्व है लेकिन बराबर नहीं
(ii) दोनों `Rf’(x_(0))` तथा `Lf’(x_(0))` में से कोई एक सीमित नहीं है
(iii) दोनों `Rf’(x_(0))Lf’(x_(0))` में से किसी एक का अस्तित्व नहीं है तब निम्न प्रश्नों को हल कीजिए।
फलन `f(x)="max".{x^(2),(x-1)^(2),2x(1-x)},0lexle1` परिभाषित किया जाता है
View Solutionएक फलन f समुच्चय X से Y तक आच्छादक है। यदि प्रत्येक `y epsilon Y` के लिए `x epsilon X` का अस्तित्व इस प्रकार है कि `f(x)=y` यदि नहीं हो तो इसके विपरीत लिया जाता है यदि एक वास्तविक फलन आच्छादक होगा यदि यह सभी वास्तविक मानों को लेता है अन्यथा एक अंतः क्षेपी फलन होगा अतः यदि X तथा Y सीमित समुच्चय है तो f आच्छादक नहीं हो सकता यदि Y,X से अधिक अवयवों को लेता है।
निम्न में से कौन सा फलन आच्छादक नहीं है
View Solutionएक फलन f समुच्चय X से Y तक आच्छादक है। यदि प्रत्येक `y epsilon Y` के लिए `x epsilon X` का अस्तित्व इस प्रकार है कि `f(x)=y` यदि नहीं हो तो इसके विपरीत लिया जाता है यदि एक वास्तविक फलन आच्छादक होगा यदि यह सभी वास्तविक मानों को लेता है अन्यथा एक अंतः क्षेपी फलन होगा अतः यदि X तथा Y सीमित समुच्चय है तो f आच्छादक नहीं हो सकता यदि Y,X से अधिक अवयवों को लेता है।
बहुपद फलन `a_(0)x^(n)+a_(1)x^(n-1)+…………+a_(n)=0,a_(0)!=0` आच्छादक है यदि
View Solutionएक फलन f समुच्चय X से Y तक आच्छादक है। यदि प्रत्येक `y epsilon Y` के लिए `x epsilon X` का अस्तित्व इस प्रकार है कि `f(x)=y` यदि नहीं हो तो इसके विपरीत लिया जाता है यदि एक वास्तविक फलन आच्छादक होगा यदि यह सभी वास्तविक मानों को लेता है अन्यथा एक अंतः क्षेपी फलन होगा अतः यदि X तथा Y सीमित समुच्चय है तो f आच्छादक नहीं हो सकता यदि Y,X से अधिक अवयवों को लेता है।
फलन `f(x)=3x+sinx` जहां `x epsilon R` है
View Solutionएक फलन f समुच्चय X से Y तक आच्छादक है। यदि प्रत्येक `y epsilon Y` के लिए `x epsilon X` का अस्तित्व इस प्रकार है कि `f(x)=y` यदि नहीं हो तो इसके विपरीत लिया जाता है यदि एक वास्तविक फलन आच्छादक होगा यदि यह सभी वास्तविक मानों को लेता है अन्यथा एक अंतः क्षेपी फलन होगा अतः यदि X तथा Y सीमित समुच्चय है तो f आच्छादक नहीं हो सकता यदि Y,X से अधिक अवयवों को लेता है।
फलन `f(x)=(x^(2)+2x+k)/(x^(2)+4x+3k)` आच्छादक है तो
View Solutionएक फलन f समुच्चय X से Y तक आच्छादक है। यदि प्रत्येक `y epsilon Y` के लिए `x epsilon X` का अस्तित्व इस प्रकार है कि `f(x)=y` यदि नहीं हो तो इसके विपरीत लिया जाता है यदि एक वास्तविक फलन आच्छादक होगा यदि यह सभी वास्तविक मानों को लेता है अन्यथा एक अंतः क्षेपी फलन होगा अतः यदि X तथा Y सीमित समुच्चय है तो f आच्छादक नहीं हो सकता यदि Y,X से अधिक अवयवों को लेता है।
निम्न में से कौन सा फलन आच्छादक नहीं है
View Solutionयदि `f:NtoR` एक फलन होगा जो निम्नलिखित स्थितियों को संतुष्ट करता है `f(1)=1//2` तथा `f(1)+2f(2)+3f(3)+……………+nf(n)=n(n+1)f(n),nge2` के लिए
यदि `f(1003)=1/K` है तब K बराबर है
View Solutionयदि `f:NtoR` एक फलन होगा जो निम्नलिखित स्थितियों को संतुष्ट करता है `f(1)=1` तथा `f(1)+2f(2)+3f(3)+……………+nf(n)=n(n+1)f(n),nge2` के लिए
f(999) का मान `1/K` है जहां K बराबर है
View Solutionयदि `f:NtoR` एक फलन होगा जो निम्नलिखित स्थितियों को संतुष्ट करता है `f(1)=1` तथा `f(1)+2f(2)+3f(3)+……………+nf(n)=n(n+1)f(n),nge2` के लिए
f(1),f(2),f(3),f(4)………….. एक श्रेणी को प्रदर्शित करता है
View Solutionबिंदु A से एक स्पर्श रेखा इकाई त्रिज्या के वृत्त पर खींची जाती है रेखा खण्ड AB खींचा जाता है जिसकी लम्बाई चाप AC की लम्बाई के बराबर है एक सरल रेखा BC खींची जाती है । जो बढ़ाए गए वृत्त के व्यास AO के अंतिम बिंदु P पर प्रतिच्छेद करती है।
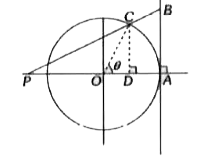
`lim_(theta to 0^(+))PA` का मान है
View Solutionबिंदु A से एक स्पर्श रेखा इकाई त्रिज्या के वृत्त पर खींची जाती है रेखा खण्ड AB खींचा जाता है जिसकी लम्बाई चाप AC की लम्बाई के बराबर है एक सरल रेखा BC खींची जाती है । जो बढ़ाए गए वृत्त के व्यास AO के अंतिम बिंदु P पर प्रतिच्छेद करती है।
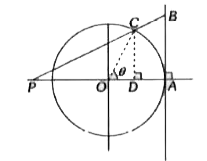
यदि C पर स्पर्श रेखा बढ़ाए गए PA के बिंदु O पर प्रतिच्छेद करती है तब `DeltaCPQ` का क्षेत्रफल है
View Solutionबिंदु A से एक स्पर्श रेखा इकाई त्रिज्या के वृत्त पर खींची जाती है रेखा खण्ड AB खींचा जाता है जिसकी लम्बाई चाप AC की लम्बाई के बराबर है एक सरल रेखा BC खींची जाती है । जो बढ़ाए गए वृत्त के व्यास AO के अंतिम बिंदु P पर प्रतिच्छेद करती है।
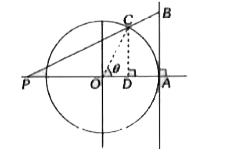
`lim_(theta to 0^(+)) ("क्षेत्रफल"(DeltaCPO))/(sin^(2)theta)` का मान है
View Solutionदिया गया है कि प्रत्येक `a epsilon (0,1)` के लिए सभी `lim_(hto0^(+))int_(h)^(1-h)t^(-a)(1-t)^(a-1)dt`
वास्तव में है। माना कि यह सीमा g(a) है इसके अतिरिक्त यह भी दिया गया है कि अंतराल (0,1) पर फलन g(a) अवकलनीय है।
`g(1/2)` का मान है
View Solutionदिया गया है कि प्रत्येक `a epsilon (0,1)` के लिए सभी `lim_(hto0^(+))int_(h)^(1-h)t^(-a)(1-t)^(a-1)dt`
वास्तव में है। माना कि यह सीमा g(a) है इसके अतिरिक्त यह भी दिया गया है कि अंतराल (0,1) पर फलन g(a) अवकलनीय है।
`g'(1/2)` का मान है
View Solutionx के पूर्णांक मानों के संख्या, जिसके लिए
`(((pi)/2^(tan^(-1)x)-4)(x-4)(x-10))/(x!-(x-1)!)lt0` है यदि `f:R^(+)toR` एक फलन है जो `x,ygt0` के लिए `f(x)f(y)=f(xy)=2(1/x+1/y+1)` को संतुष्ट करता है तब f(1/2) के संभावित मान है।
View Solutionx के पूर्णांक मानों की संख्या, जिसके लिए फलन `sqrt(sinx+cosx)+sqrt(7x-x^(2)-6)` को परिभाषित किया गया हैं
View Solutionयदि T, फलन `f(x)=[8x+7]+tan2pix+cot2pix]-8x` का आवर्तनांक है ([.] महत्म पूर्णांक फलन को दर्शाता है ) तब 1/T का मान है
View Solutionयदि `theta` फलन `f(x)=sin^(99)x+sin^(99)(x+(2pi)/3)+sin^(99)(x+(4pi)/3)`, का मूलभूत अपवर्तनांक है तो सम्मिश्र संख्या `z=|z|(cos theta+ i sin theta)` किस चतुर्थांश में है।
View Solutionयदि `f:NtoN` तथा `x_(2)gtx_(1)impliesf(x_(2))gtf(x_(1)),AA x_(1),x_(2)epsilon N` और `f(f(n))=3n, AA n epsilon N` है तब `f(2)`=
View Solutionमाना `f(x)=(ax^(8)+bx^(6)+cx^(4)+dx^(2)+15x+1)/x(x!=0` के रूप में एक फलन है यदि `f(5)=2`, तब `|f(-5)|//4` का मान है
View Solutionमाना `f(x)=(ax^(8)+bx^(6)+cx^(4)+dx^(2)+15x+1)/x(x!=0)` के रूप में एक फलन हे यदि `f(5)=2` तब `|f(-5)|//4` का मान है
View Solutionमाना कि `f:[0,4pi] to [0,pi], f(x) = cos^(-1)(cos x)` के द्वारा परिभाषित है। तब `[0,4pi]` में समीकरण `f(x) = (10-x)/10` को संतुष्ट करने वाले बिन्दुओं की संख्या है।
View Solutionएक अऋणात्मक पूर्णांक a जिसके लिए निम्न `lim_(xto1){(-ax+sin(x-1)+a)/(x+sin(x-1)-1)}^((1-x)/(1-sqrt(x))``=1/4` सत्य है तो a का अधिकतम मान है।
View Solutionमाना कि `f:RtoR` तथा `g:RtoR` क्रमशः `f(x)=|x|+1` तथा `g(x)=x^(2)+1` द्वारा परिभाषित हैं माना कि फलन `h:RtoR`
`h(x)={(max{f(x),g(x)},; xle0),(min{f(x),g(x)},; x gt0):}` द्वारा परिभाषित है। जहां h(x) अवकलनीय नहीं है उन बिंदुओं की संख्या है।
View Solutionमाना कि `f:RtoR` एक सतत विषम फलन है जिसका मान केवल एक बिंदु पर ही शून्य होता है तथा `f(1)=1/2` है। माना कि सभी `x epsilon [-1,2]` के लिए `F(x)=int_(1)^(x)f(t)dt` एवं सभी `x epsilon [-1,2]` के लिए `G(x)=int_(-1)^(x)t|f(f(t))|dt` है। यदि `lim_(xto 1)(F(x))/(G(x))=1/14` है तब `f(1/2)` का मान है।
View Solutionमाना कि दो धनात्मक पूर्णांक m और n एक 1 से बड़े है यदि `lim_(ato 0)((e^(cos(a^(n)))-e)/(alpha^(m)))=-(e/2)` तब `m/n` का मान है।
View Solutionमाना कि `alpha, beta epsilon R` इस प्रकार है कि `lim_(xto0)(x^(2)sin(betax))/(alpha x-sinx)=1` तब `6(alpha+beta)` का मान है
View Solutionमाना कि समुच्चय X में ठीक 5 अवयव हैं और समुच्चय Y में ठीक 7 अवयव हैं यदि X से Y में एकैकी फलनों की संख्या `alpha` है और Y से X में आच्छादक फलनों की संख्या `beta` है तब `1/(5!)(beta-alpha)` का मान है।
View Solutionमान लीजिए कि `f : R rarr R, f (0) = 1` के साथ एक अवकलनीय फलन है और सभी `x, y inR` के लिए समीकरण `f (x + y) = f (x)f' (y) + f' (x)f (y)` को संतुष्ट करता है। तो, `log_e` (f (4)) का मान है
View Solution
JEE ADVANCED( INTEGER TYPE) questions and complete solutions for chapter फलन, सीमा, सांतत्य तथा अवकलनीयता of ERRORLESS MATHS (HINDI) of Class 12
All Exercises from ERRORLESS HINDI Class 12 MATHS फलन, सीमा, सांतत्य तथा अवकलनीयता
- EXERCISE
- ILLUSTRATION
- JEE ADVANCED( INTEGER TYPE)
- JEE ADVANCED( MATCH THE COLUMN TYPE)
- JEE ADVANCED( MORE THAN ONE CORRECT ANSWERS)
- JEE ADVANCED( PASSAGE TYPE)
- SOLVED MULTIPLE CHOICE QUESTIONS (अवकलनीयता)
- SOLVED MULTIPLE CHOICE QUESTIONS (फलन)
- SOLVED MULTIPLE CHOICE QUESTIONS (सांतत्य)
- SOLVED MULTIPLE CHOICE QUESTIONS (सीमा)