Complete Solutions to Additional Problems of chapter PROBABILITY DISTRIBUTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY DISTRIBUTIONS |
| FULL MARKS | Additional Problems |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
Four defective oranges are accidentally mixed with sixteen good ones . Two oranges are drawn at random from the mixed lot. If the random variable X denotes the number of defective oranges then find the values of X and number of points in its iverse image.
View SolutionFind the probability mass function and the cumulative distribution function for getting 3 s when two dice are thrown.
View SolutionFor the distribution function given by `F(x)={{:(0",", x lt 0), (x^(2)",", 0 le x le 1), (1",", x gt 1):}`. Find the density function.
Also evaluate (i) `P(0.5 lt x lt 0.75)` (ii) `P(x le 0.5)` (iii) `P(X gt 0.75)`
View SolutionFor the probability density function f(x) =`{(2e""^(-2x),x gt0),(0,xlt=0):}` find F(2)
View SolutionThe probability density function of a random variable x is f(x) = `{(kx^(alpha-1)e^(-betax^alpha),x","alpha","beta","gt0),(0,"elsewhere"):}`
Find (i) k, (ii) P`(X gt 10)` .
View SolutionA continuous random variable x has the p.d.f defined by f(x) = `{(Ce""^(-ax),0ltxltoo),(0,"elsewhere"):}` find the value of C if `a gt 0.`
View SolutionAn urn contains 4 white and 3 Red balls. Find the probability distribution of the number of red balls in three draws when a ball is drawn at random with replacement . Also find its mean and variance.
View SolutionFind the mean and variance of the distribution f(x) = `{(3e""^(-3x),0lt xltoo),(0,"elsewhere"):}`
View SolutionTwo cards are drawn with replacement from a well shufflied deck of 52 cards . Find the mean and variance for the number of aces .
View SolutionIn a Binomial distribution if n = 5 and P(X=3) =2P (X=2) find p.
View SolutionIf the sum of mean and variance of a Binomial Distribution is 4.8 for 5 trials find the distribution .
View SolutionIf on an average 1 ship out of 10 do not arrive safely to parts . Find the mean and the standard deviation of the ships returining safely out of a total of 500 ships .
View SolutionThe overall percentage of passes in a certain examination is 80 . If six candidates appear in the examination what is the probability that at least five pass the examination .
View SolutionIn a hurdle race a player has to cross 10 hurdles . The probability that he will clear each hurdle is 5/6. What is the probability that he will knock down less than 2 hurdles ?
View SolutionIf f(x) = `{(kx^(2),0ltxlt 3),(0,"elsewhere"):}` is a probability density function then the value of k is ……. .
View SolutionIf f(x) = `(A)/(pi)(1)/(16+x^(2)),0 ltx lt oo` is a probability density function of a continuous random variable X then the value of A is ……… .
View SolutionA random variable X has the following probability mass function as follows :
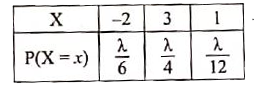
Then the value of `lambda ` is …………. .
View SolutionX is a discrete random variable which takes the values of 0,1,2 and P (X=0) = `(144)/(169)` P(X=1) = `(1)/(169)` then the value of P(X=2) is ………. .
View SolutionGiven E(X+C)=8 and E(X-C)=12 The value of C is
View SolutionX is a random variable taking the values 3,4 and 12 with probabilites `1/3,1/4` and `5/12` then E(x) is
View SolutionVariance of the random variable X is 4 . Its mean is 2 . Then E`(X^(2))` is …………. .
View SolutionIn 5 throws of a die getting 1 or 2 is a success . Then mean number of success is ………. .
View SolutionThe mean of a binomial distrution 5 and SD is 2, Then the value of n and p are :
View SolutionIf the mean and standard deviation of a binomial distribution are 12 and 2 respectively . Then the value of its parameter p is ………….. .
View SolutionA box contains 6 red and 4 white balls . If 3 balls are drawn at random the probability of getting 2 white balls without replacement is ………… .
View SolutionIf 2 cards are drawn from a well shuffled pack of 52 cards the probability that they are of the same colours without replacement is ………… .
View SolutionThe distribution function F(x) of a random variable X is ……….
View Solution
Additional Problems questions and complete solutions for chapter PROBABILITY DISTRIBUTIONS of FULL MARKS MATHS (TAMIL ENGLISH) of Class 12