Complete Solutions to Example Questions Solved of chapter PROBABILITY DISTRIBUTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY DISTRIBUTIONS |
| FULL MARKS | Example Questions Solved |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
Suppose two coins are tossed once. If X denotes the number of talls (i) write down the sample space (ii) find the inverse image of 1 (iii) the values of the random variable and number of elements in its inverse images .
View SolutionSuppose a pair of unbiased dice is rolled once if X denotes the total score of two dice write down
Sample space
View SolutionAn urn contains 2 white balls and 3 red balls . A sample of 3 balls are chosen at random from the urn. If X denotes the number of red balls chosen find the values taken by the random variable X and its number of inverse images .
View SolutionTwo balls are chosen randomly from an urn containing 6 white and 4 black balls . Suppose that we win ₹ 30 for each black ball selected and we lose ₹ 20 for each white ball selected. If X denotes the winning amount then find the values of X and number of points in its inverse images .
View SolutionThree fair coins are tossed simultaneously. Find the probability mass function for number of heads occurred.
View SolutionA pair of fair dice is rolled once . Find the probability mass function to get the number of fours .
View SolutionIf the probability mass function f(x) of a random variable X is

find (i) its cumulative distribution hence find (ii) P (X `lt=`3) and , (iii) `P( X gt=2)`
View SolutionA six sided die is marked 1 on one face 2 on two of its faces and 3 on remaining three faces . The die is rolled twice . If X denotes the total score in two throws .
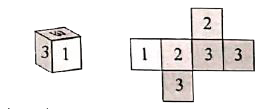
View SolutionFind the probability mass function f(x) of the discrete random variable X whose cumulative distribution function F(x) is given by F (x) = `{(0,-ooltxlt-2),(0.25,-2lt=xlt-1),(0.60,-1lt=xlt0),(0.90,0lt=xlt1),(1,1lt=xltoo):}`
Also find (i) P (X`lt0` ) and (ii) P`(Xgt=-1)`.
View SolutionA random variable X has the following probability mass function.Find the value of K

View SolutionFind the constant C such that the function f(x) = `{(Cx^(2),1ltxlt4),(0,"Otherwise"):}`
is a density function and compute (i) P `(1.5 lt X lt 3.5) "(ii)" P(Xlt=2) "(iii)" P (3lt X )` .
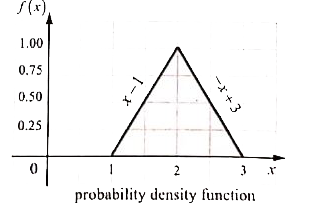
View SolutionIf X is the random variable with porbability density function f(x) given by `f(x)={(x-1,1lt=xlt2),(-x+3,2lt=xlt3),(0,"otherwise"):}`
find (i) the distribution function F(x) (ii) P`(1.5lt=X lt=2.5)`
View SolutionIf X is the random variable with distribution function F(x) given by , F(x) =`{(o,xlt0),(x,0lt=xlt1),(1,1lt=x):}` then find (i) the probability density function f(x) (ii) `P(0.2lt=Xlt=0.7)` .
View SolutionThe probability density function of random variable X is given by f(x)=`{(k,1lt=xlt5),(0,"otherwise"):}`
Find (i) Distribution function (ii) `P(X lt 3) " (iii)" P(2ltX lt4) "(iv)" P(3 lt=X)`
View SolutionThe probability density function of X is given by f(x) = `{(ke^(-x/3),"for" " "xgt0),(0, "for" " " xlt=0):}`
Find (i) the value of k (ii) the distribution function (iii) `P(X lt 3)` (iv) `P(5lt=X)` (v) `P(X lt=4)` .
View SolutionSuppose that f(x) given below represents a probability mass function

Find (i) the value of c (ii) Mean and variance.
View SolutionTwo balls are chosen randomly from an urn containing 8 white and 4 black balls. Suppose that we win Rs 20 for each black ball selected and we lose Rs 10 for each white ball selected . Find the expected winning amout and variance.
View SolutionFind the mean and variance of a random variable X , whose probability function is f(x) = `{(lambdae^(-lambdax),"for"" "xgt=0),(0,"otherwise"):}`
View SolutionThe mean and variance of a binomial variate X are respectively 2 and 1.5 . Find (i) P(X=0) (ii) P(X=1) (iii) P`(Xgt=1)`
View Solution
Example Questions Solved questions and complete solutions for chapter PROBABILITY DISTRIBUTIONS of FULL MARKS MATHS (TAMIL ENGLISH) of Class 12