Complete Solutions to EXERCISE -11.6 of chapter PROBABILITY DISTRIBUTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY DISTRIBUTIONS |
| FULL MARKS | EXERCISE -11.6 |
| Number Of Questions | 20 |
| Academic Year | 2023-24 |
Let X be random variable with probability density function
`f(x)={{:(2/x^(3), x ge 1), (0, x lt 1):}`
Which of the following statement is correct
View SolutionA rod of length 2l is broken into two pieces at random. The probability density function of the shorter of the two pieces is
`f(x)={{:(1/l, 0 lt x ge l), (0, l le x lt 2l):}`
The mean and variance of the shorter of the two pieces are respectively
View SolutionConsider a game where the player tosses a six sided fair die. If the face that comes up is 6, the player wins Rs. 36, otherwise he loses Rs. `k^(2)`, where k is the face that comes up k = {1, 2, 3, 4, 5}.
The expected amount to win at this game in Rs. is
View SolutionA pair of dice numbered 1, 2, 3, 4, 5, 6 of a six-sided die and 1, 2, 3, 4 of a four-sided die is rolled and the sum is determined. Let the random variable X denote this sum. Then the number of elements in the inverse image of 7 is
View SolutionA random variable X has binominal distribution with n = 25 and p = 0.8 then standard deviation of X is
View SolutionLet X represent the difference between the number of heads and the number of tails obtained when a coin is tossed n times. Then the possible values of X are
View SolutionIf the function `f(x)=1/12 " for " a lt x lt b`, represents a probability density function of a continuous random variable X, then which of the following cannot be the value of a and b?
View SolutionFour buses carrying 160 students from the same school arrive at a football stadium. The buses carry, respectively, 42, 36, 34, and 48 students. One of the students is randomly selected. Let X denote the number of students that were on the bus carrying the randomly selected student. Let Y denote the number of students on that bus. Then E[X] and E[Y] respectively are
View SolutionTwo coins are to be flipped. The first coin will land on heads with probability 0.6, the second with probability 0.5. Assume that the results of the flips are independent, and let X equal the total number of heads that result. The value of E[X] is
View SolutionOn a multiple-choice exam with 3 possible destructive for each of the 5 questions, the probability that a student will get 4 or more correct answers just by guessing is
View SolutionIf P{X=0}=1-P{X=1}. If E{X}=3Var(X), then P{X=0} is
View SolutionIf X is a binomial random variable with expected value 6 and variance 2.4, then P(X=5) is
View SolutionThe random variable X has the probability density function `f(x)={{:(ax+b, 0 lt x lt 1), (0, "otherwise"):}` and `E(X)=7/12`, then a and b are respectively
View SolutionSuppose that X takes on one of the values 0, 1, and 2. If for some constant k, P(X=i)=k P(X=i-1)i=1,2 and P(X=0)=`1/7` then the value of k is
View SolutionWhich of the following is a discrete random variable?
I. The number of cars crossing a particular signal in a day.
II. The number of customers in a queue to buy train tickets at a moment.
III. The time taken to complete a telephone call.
View SolutionIf f(x) = `{(2x,0 lt=xlt=a),(0,"otherwise"):}` is a probability density function of a random variable then the value of a is ……….. .
View SolutionThe probability function of a random variable is defined as
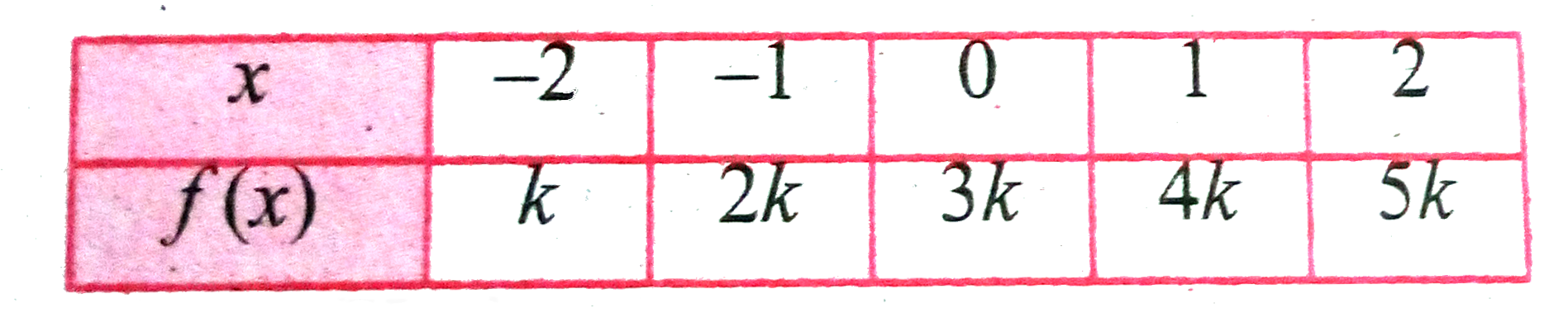
Then E(X) is equal to
View SolutionLet X have a Bernoulli distribution with mean 0.4, then the variance of (2X-3) is
View SolutionIf in 6 trials, X is a binomial variate which follows the relation 9P(X=4)=P(X=2), then the probability of success is
View SolutionA computer salesperson knows from his past experience that he sells computers to one in every twenty customers who enter the showroom. What is the probability that he will sell a computer to exactly two of the next three customers?
View Solution
EXERCISE -11.6 questions and complete solutions for chapter PROBABILITY DISTRIBUTIONS of FULL MARKS MATHS (TAMIL ENGLISH) of Class 12