Complete Solutions to Solved Examples of chapter PERMUTATIONS - FOR BOARDS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PERMUTATIONS - FOR BOARDS |
| KC SINHA | Solved Examples |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
There sre three letters asnd three envelopes. Find the total number of wys in which letters can be put into the envelopes so that each envelope has only one letter.
View SolutionFind the number of possible outcomes of tossing a coin twice.
View SolutionIn a class tghere are 20 boys and 15 girls. In how many ways can the techer select one boy and one girl from amongst the students of the class to represent the schoo,l in a quiz competition?
View SolutionA teacher has to select either a boy or a girl from a clas of 12 boys and 15 girls for coordinating a school function. In how many ways can she do it?
View SolutionThere are 5 routes ferom A to B and 3 routes from place B to place C. Find how many different routes are there from A to C via B.
View SolutionHow many 3 letter code combinations are possible using the first 10 letters of English alphbets if: i. no letter can be repeated, ii. letters can be repeated.
View SolutionIf there are 20 buses playing between places A and B, in how many ways can a round trip from A be made if the return journey was made on: i. the same bus, ii. a different bus.
View SolutionThere are 4 multiple choice questions in an examination. How many sequences of answers are possible, if each question has 2 choices?
View SolutionA coin is tossed three times and the outcomes are recorded. How many possible outcomes are there? How many possible outcomes if the coin is tossed four times? Five times? `n` times?
View SolutionA gentle man want to invite six friends. In how many ways and he send invitation cards to them, if he has three servants to carry the cards.
View SolutionFind the number of odd positive numbers which have three digits.
View SolutionHow many odd numbers less than 1000 can be formed using the digits 0, 1, 4, and 7 if repetition of digits is allowed?
View SolutionFind the number of different signals that can be made by arranging at least 3 flags in order on a vertical pole, if 6 different flags are available.
View SolutionHow many three digit numbers are there such that atleast one of their digits is 7?
View SolutionIn how many ways can five people be seated in a car with two people in the front seat and three in the rear, if two particular persons out of the five cannot drive?
View SolutionIn how many ways can 5 different balls be distributed among three boxes?
View SolutionHow many A.P.s with 10 terms are there whose first term is in the set {1,2,3} and whose common difference is in the set {1,2,3,4,5}?
View SolutionHow many non-zero numbers can be formed using the digits 0,1,2,3,4 and 5 if repetition of digits is not allowed?
View SolutionA class consists of 40 girls and 60 boys. In how many ways can a president, vice president, treasurer and secretary be chosen i th treasurer must be a girl, the secretary must be a boy and a student may not hold more than one office?
View SolutionFind the total number of ways in which n distinct objects can be put into two different boxes so that no box remains empty.
View SolutionA team consisting of 7 boys and 3 girls plays singles matches against another team consisting of 5 boys and 5 girls. How many matches can be scheduled between the two teams if a boy plays against a girl and a girl plays against a boy?
View SolutionFind: `[7!]/[6!]`
View SolutionFind : `[6!]/[2xx4!]`
View SolutionCompute: `[52!]/[48!4!]`
View SolutionCompute: ` [7!]/[4!2!]`
View SolutionConvert the following products into factorial: `5. 6. 7. 8. 9. 1`
View SolutionConvert the following products into factorial: 2.4.6.8.10
View SolutionIf `1/(9!)+1/(10 !)=x/(11 !)` , find `xdot`
View SolutionProve that `(n!)^(2) lt n^(n) n! lt (2n)!` for all positive integers n.
View SolutionFind the L.C.M. And H.C.F. or 5!,6! And 7!
View SolutionProve that `((2n+1)!)/(n !)=2^n{1. 3. 5 .........(2n-1)(2n+1)}`
View Solutionabout to only mathematics
View SolutionProve that (n!+1) is not divisible by any natural number between 2 and n.
View SolutionProve that ` nP_n=2 ^nP_(n-2) `
View SolutionFind `n` if `""^(n-1)P_(3): ""^(n)P_(4) = 1:9`.
View SolutionFind r, if `5^4P_r=6^5P_(r-1)`.
View SolutionFind the value of n such that
` "(i) "^(n)P_(5) =42 xx ""^(n)P_(3), n gt 4 " (ii) "(""^(n)P_(4))/(" "^(n-1)P_(4))=(5)/(3), n gt 4.`
View SolutionIf `\ ^n P_4=360 ,\ ` find the value of `ndot`
View SolutionIf `^nP_3=9240`, find n
View SolutionIf `.^(n)P_(r) = 720` and `.^(n)C_(r) = 120`, then find r.
.
View SolutionIf `"^(2n+1)P_(n-1):^(2n-1)P_n=3:5,` then find the value of `n`.
View Solutionprove that `1P_1+2.2P_2+3.3P_3+.........+n.nP_n=(n+1)P_(n+1)-1`
View SolutionHow many numbers of four digits can be formed with the digits 1,2,3,4, and 5? (if repetition of digits is not allowed).
View SolutionHow many numbers lying between 100 and 1000 can be formed with the digits 0, 1, 2, 3, 4, 5, if the repetition of the digits is not allowed?
View SolutionHow many numbers greater than 40000 can be formed using the digits 1,2,3,4 and 5 if each digit is used only once in each number?
View SolutionHow many different 4-digit numbers can be formed from the digits 2,3,4 and 5 if each digits is used only once in as number ? Further, how many of these numbers i. end in a 4? ii.end in a 3? iii. End in a 3 or 6?
View SolutionFind the number oif numbers between 300 and 3000 which can be formed with the digits 0,1,2,3,4 and 5 no digit being repeated in any number.
View SolutionHow many odd numbers greter than 8000 can be formed using the digits 2,3,4,5 nd 8 if each digit is used only once in each number?
View SolutionHow many even numbers of four digits can be formed with the digits 0,1,2,3,4,5 and 6 no digit being used more than once?
View SolutionHow many even numbers are there with three digits such that if 5 is one of the digits, then 7is the next digit?
View SolutionHow many numbers of six digits can be formed from the digits 0,1,3,5,7 and 9 when no digit is repeated? How many of them are divisible by 10?
View SolutionHow many positive numbers can be formed by using any number of the digits 0,1,2,3 and 4 no digit being repeted in any number?
View SolutionHow many numbers can be formed with the digits 1, 2, 3, 4, 3, 2, 1 so that the odd digits always occupy the odd places?
View SolutionHow many numbers greater than a million casn be formed with the digits 2,3,0,3,4,2,3?
View SolutionHow many numbers of four digits greater than `2300` can be formed with the digits `0, 1, 2, 3, 4,5 and 6;` no digit being repeated in any number?
View SolutionHow many four digit natural numbers not exceeding 4321 can be formed with the digits 1, 2, 3 and 4, if the digits can repeat?
View SolutionHow many different 4-digit number can be formed with the digits 1,2,3,4 without any repetition ? Also find their sum.
View SolutionFind the sum of all the four digit numbers which can be formed with the digits 0,1,2 and 3.
View SolutionFind the sum of all those 4 digits numbers which can be formed with the digits 1,2,3,4.
View SolutionA gentle man wants to invite six friends. In how many ways can he send invitation cards to them, if he has three servants to carry the cards.
View SolutionIn how many ways 3 prizes can be given away to 7 boys when each boy is eligible for any of the prizes.
View SolutionHow many numbers greater than 1000, but not greater than 4000 can be formed with the digits 0, 1, 2, 3, 4 if: (i) repetition of digits is allowed? (ii) repetition of digits is not allowed?
View SolutionA telegraph has 5 arms and each arm is capable of 4 distinct positons, including the position of rest. What is the total number of signals that can be made?
View SolutionA letter lock consists of three rings each marked with 10 different letters. In how many ways it is possible to make an unsuccessful attempt to open the lock?
View SolutionThe lock of a safe has a dial with holes, sasy ten, in which the numbers 0,1,2,……..9 are inscribed in each hole. The lock can be opened only when a specific code numbersay of six digits is dialled. Suppose the code number is 249916, it means that the can be opened when we first dial 2, then 4 nd so on. Find the maximum number of trials which do not result in opening the lock.
View SolutionTen different letters of an alphabet are given. Words with five letters are formed from these given letters. Determine the number4 of words which have at least one letter repeated.
View SolutionIn how many ways can 8 Indians, 4 Americans and 4 Englilshmen be seated in a erow so that all persons of the same nationaslity sit together.
View SolutionA shelf contains 20 books of which 4 are single volume and the other form sets of 8, 5, and 3 volumes. Find the number of ways in which the books may be arranged on the shelf so that
(i) volumes of each set will not be separated,
(ii) volumes of each set remain in their due order.
View SolutionA library has two books each having three copies and three other books each having tow copies. In how many ways can all these books be arranged in a shelf so that copies of the same book are not separated.
View SolutionThree married couples are to be seated in a row having six seats in a cinema hall. If spouses are to be seated next to each other, in how many ways can they be seated? Find also the number of ways of their seating if all the ladies sit together.
View SolutionIn how many ways can 10 examination papers be arranged so that the best and worst papers never come together?
View SolutionThere are 5 boys and 3 girls. In how many ways can they be seated in a row so that al the three girls do not sit together
View SolutionIn how many ways can 5 boys and 3 girls sit in a row so that no two girls are sit together?
View SolutionIn how many of the distinct permutations of the letters in MISSISSIPPI do the four s not come together?
View SolutionIn how many ways can 7 I. A and 5 I.Sc. Students be seated in a row so that no tow f the I.Sc students may sit together?
View SolutionIn a class of 10 students there are 3 girls A, B, C. In how many different ways can they be arranged in a row such that no two of the here girls are consecutive.
View SolutionIn how many ways 4 boys and 4 girls can be seated in a row so that boys and girls are alternate?
View SolutionIn how many ways 4 boys and 3 girls can be seated in a row so that they are alternate?
View SolutionIn how many ways 10 Indians, 5 Asmericans and 4 Englishmen can be seasted in a row so that neither Americans nor Englishmen sit between Indians.
View SolutionA customer forgets a foru-digit code for an Automatic Teller Machine (ATM) in a bank. However, he remembers that this code consists of digits 3,5,6 and 9. Find the largest possible nuim,ber of trials necessary to obtain the correct code.
View SolutionA number lock on a suitcase has 3 wheels each labelled with ten digits 0 to 9. If opening of the lock is a particular sequence of three digits with no repeats, how many such sequences will be possible? Also, find the number of unsuccessful attempts to open the lock.
View SolutionThere are 6 items in column A and 6 items in column B. A student is asked to match each item in column A with an item in column B. How many possible, correct or incorrect, answer are there to this question?
View SolutionHow many different signals can be made by 5 flags from 8 flags of different colours?
View SolutionSerial numbers for an item produced in a factory are to be made using two letters followed by four digits (0 to 9). If the letters are to be taken from six letters of English alphabet without repetition and the digits are also not repeated in a serial number, how many serial numbers are possible?
View SolutionIn how many distinct ways can the product `xy^2z^2` be written without using exponents?
View SolutionThere are 3 white, 4 red and 1 blue marbles in a bag. They are drawn one by one and arranged in a row. Assuming that all the 8 marbles are drawn, determine the number of different arrangements if marbles of same colour are indistinguishable.
View SolutionIn how many ways can 5 flags, in which 3 are red, one is white and one is blue, be arranged on a staff, one below the other, if flags of one colour are not distinguishable?
View SolutionA biologist studying the genetic code is interested to know the number of possible arrangements of 12 molecules in a chain. The chain contains 4 different molecules represented by the initials A(for a Adenine), C (for Cytosine), G (for Guanine) and T (for Thymine) and 3 molecules of each kind. How many different such arrangements are possible?
View SolutionFind the number of permutations of the letters of the word PRE-UNIVERSITY.
View SolutionIn how many ways can the letters of the word 'CIVILIZATION' be rearranged?
View SolutionHow many words can be formed with the letters of the word UNIVERSITY, the vowels doesnt remain together?
View SolutionIn how many ways can the letters of the word DIRECTOR be arranged so that the three vowels are never together?
View SolutionFind the number of rearrangements of the letters of the word BENEVOLENT. How many them end in L?
View SolutionIn how many ways can the letters of the word 'ALGEBRA' be arranged, so that two A's are never together?
View SolutionHow many words can be formed with the letters of thw word 'PATALIPUTRA' without changing the relative positions of vowels and consonants?
View SolutionhHow many different words can be formed with the letters of the word PENCIL when vowels occupy even places.
View SolutionIn how many ways can the letters of he word ARRANGE be arranged so that the two A\'s are together but not two R\'s
View SolutionIt is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible ?
View SolutionHow many different words casn be formed with five given letters of which three are vowels and two are consonants, no tow vowels being together in any word?
View SolutionA person is to walk from A to B. However, he is restricted to walk only to the right of A or upwards of A. but not necessarily in the order shown in the figure. Then find the number of paths from A to B.
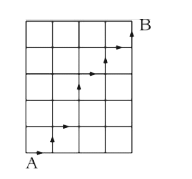
View Solution
Solved Examples questions and complete solutions for chapter PERMUTATIONS - FOR BOARDS of KC SINHA ENGLISH of Class 12