Complete Solutions to Part 1 Mathematics of chapter KVPY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | KVPY |
| KVPY | Part 1 Mathematics |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
The number of pairs (a, b) of positive real numbers satisfying `a^(4)+b^(4)lt1" and "a^(2)+b^(2)gt1` is
03:18View SolutionThe number of real roots of the polynomial equation `x^(4)-x^(2)+2x-1=0` is
01:36View SolutionSuppose the sum of the first m teams of a arithmetic progression is n and the sum of its first n terms is m, where `mnen.` Then the sum of the first (m + n) terms of the arithmetic progression is
04:33View SolutionConsider the following two statement:
I. Any pair of consistent linear equations in two variables must have unique solutions.
II. There do not exist two consecutive integers, the sum of whose squares is 365.
Then03:39View SolutionThe number of polynomials p(x) with integer coefficients such that the curve y = p(x) passes through (2, 2) and (4, 5) is
02:26View Solutionfind the sum of all three digit natural numbers which are divisible by `7`
03:28View SolutionA solid hemisphere is attached to the top of a cylinder, having the same radius as that of the cylinder. If the height of the cylinder were doubled (keeping both radii fixed), the volume of the entire system would have increased by 50%. By what percentage would the volue have increased if the radii of the hemisphere and the cylinder were doubled (keeping the height fixed)?
06:20View SolutionConsider a triangle PQR in which the relation `QR^(2)+PR^(2)=5PQ^(2)` holds. Let G be the point of intersection of medians PM and QN. Then `angleQGM` is always
08:59View SolutionLet a, b, c be the side-lengths of a triangle, and l, m,n be the lengths of its medians. Put `K=((l+m+n)/(a+b+c))` Then, as a, b, c vary, K can assume every value in the interval
02:26View SolutionLet `x_(0), y_(0)` be fixed real numbers such that `x_(0)^(2)+y_(0)^(2)gt1`. If x, y are arbitrary real numbers such that `x^(2)+y^(2)le1`, then the minimum value of `(x-x_(0))^(2)+(y-y_(0))^(2)` is
02:38View SolutionLet PQR be a triangle which PQ = 3. Form the vertex R, draw the altitude RS to meet PQ at S. Assume that `RS=sqrt3" and " Ps=QR`. Then PR equals
02:01View SolutionA 100 mark examination was administered to a class of 50 students. Despite only integer marks being given, the everge score of the class was 47.5. Then , the maximum number of students who could get marks more than the class average is
02:50View SolutionLets be the sum of the digits of the number `15^(2)xx5^(18)` in base 10. Then
02:52View SolutionLet PQR be am acute-angled triangle in which PQ lt QR. From the vertex Q draw altitude `QQ_(1)`, the angle bisector `Q Q_(2)` and the median`Q Q_(3)" With "Q_(1),Q_(2),Q_(3)` lying on PR. Then
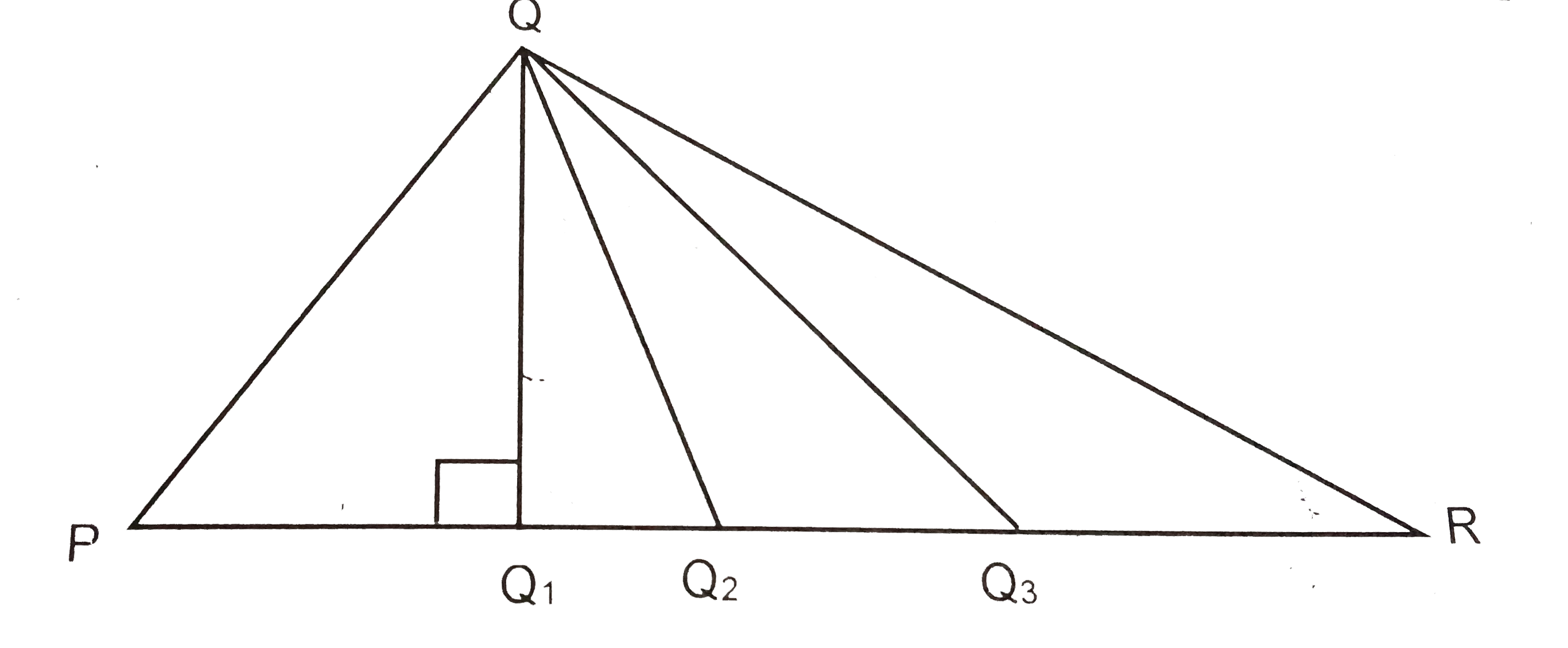 01:28View Solution
01:28View SolutionAll the vertices of a rectangle are of the form (a, b) with a, b integers satisfying the equation `(a-8)^(2)-(b-7)^(2)=5`. Then the perimeter of the rectangle is
03:54View SolutionLet r be a root of the equation `x^(2)+2x+6=0.` The value of `(r+2)(r+3)(r+4)(r+5)` is equal to-
03:23View SolutionLet R be the set of all real numbers and let f be a function from R to R such that
`f(X)+(X+1/2)f(l-X)=1,`
for all `xinR." Then " 2f(0)+3f(1)` is equal to-04:51View SolutionThe sum of all positive integers n for which `(1^3+2^3+....(2n)^3)/(1^2+2^2+....+n^2)` is also an integer is
03:09View SolutionLet x and y be two 2-digit numbers such that y is obtained by recersing the digits of x. Suppose they also satisfy `x^(2)-y^(2)=m^(2)` for same positive integer m. The value of x + y + m is-
07:23View SolutionLet `p(x)=x^(2)-5x" and "q(x)-3x+b`, where a and b are positive integers. Suppose hef `(p(x),q((x))=x-1" and "k(x)=1cm(p(x),q(x))`. If the coefficient of the highest degree term of k(x) is 1, the sum of the roots of (x - 1)+ k(x) is-
02:03View SolutionIn a quadrilateral ABCD, which is not a trapezium, it is known that `angle DAB=angle ABC=60^(2)`. Moreover `angle CAB = angle CBD`. Then
02:18View SolutionA semi-circle of diameter 1 unit sits at the top of a semi-circle of diameter2 units. The shaded region inside the smaller semi-cricle but outside the larger semi-circle a lune. The area of the lune is-
 05:50View Solution
05:50View SolutionThe angle biosectors BD and CE of a triangle ABC are divied by the incentre 1 in the rartios 3 : 2 and 2 : 1 respecticely. Then the ratio in which I divides the bisector through A is-
03:28View SolutionSuppose `S_(1)" and "S_(2)` are two unequal circles, AB and CD are the direct common tangents to these circles. A transverse common tangent PQ cuts AB in R and CD in S. If AB = 10, then RS is -
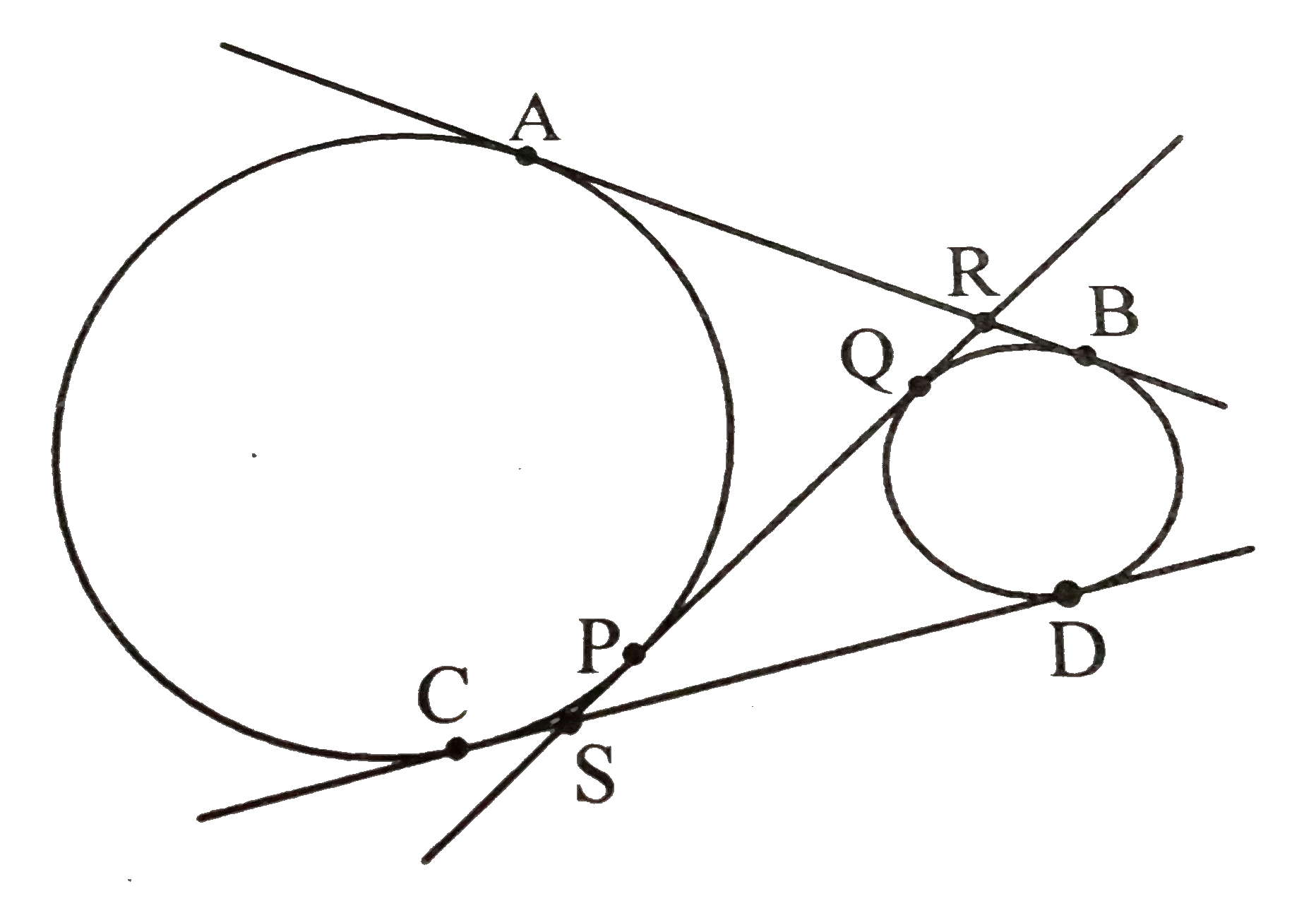 03:37View Solution
03:37View SolutionOn the circle with centre O, points A, B are such that OA =AB. A point C is located on the tangent at B to the circle such that A and C are on the opposite sides of the line OB and Ab =BC. The line segment AC intersects the circle again at F. Then the ratio `angleBOF: angle BOC` is equal to-
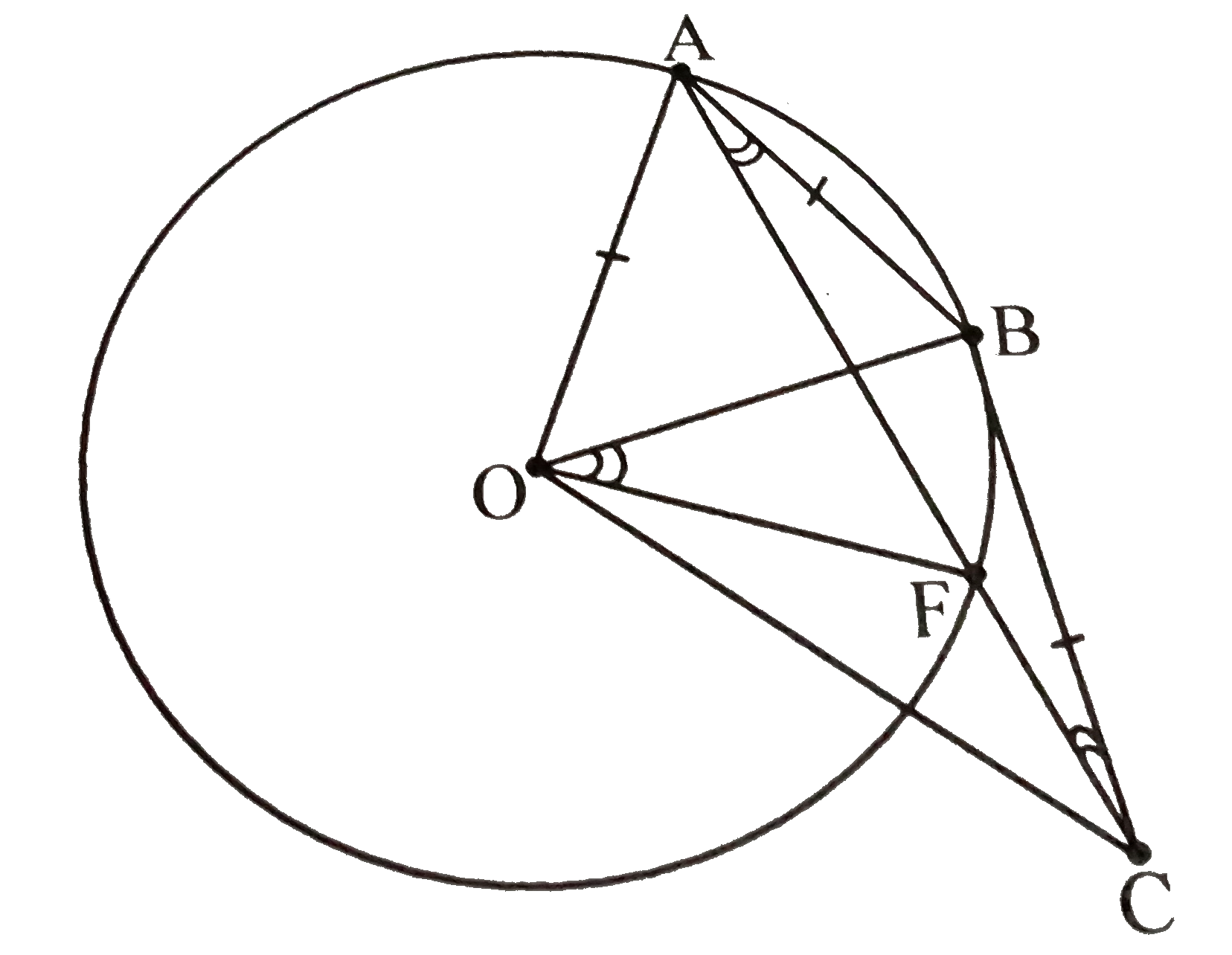 03:26View Solution
03:26View SolutionIn a cinema hall, the charge per person is RS. 200. On the first day, only 60% of the seats were filled. The owner decided to reduce the price by 20% abd there was an increasesof 50% in the number of spectators on the next day. The percentage increase in the revenue on the second day was-
04:59View SolutionThe population of cattle in a farm increases so that the difference between the populationin year n + 2 and that in year n is proportional to the population in year n + 1. If the populations in years 2010, 2011 and 2013 were 39, 60 and 123, respectively, then the population in 2012 was-
04:18View SolutionFind the number of 6-digit numbers of the form ababab (in base 10) each of which is a product of exactly `6 `distinct primes.
04:14View SolutionThe houses on one side of a road are numbered using consecutive even numbers .The sum of the numbers of all the houses in that row is 170. If there are at least 6 houses in that row and a is the number of the sixth house then
04:03View SolutionSuppose `a_(2),a_(3),a_(4),a_(5),a_(6),a_(7)` are integers such that
`5/7=(a_(2))/(2!)+(a_(3))/(3!)+(a_(4))/(4!)+(a_(5))/(5!)+(a_(6))/(6!)+(a_(7))/(7!),`
where `0lea_(j)ltj"for "j=2,3,4,5,6,7.` The sum `a_(2)+a_(3)+a_(4)+a_(5)+a_(6)+a_(7)` is-05:56View SolutionSuppose BC is a given line segment in the plane and T is a scalene triangle. The number of points A in the plane such that the triangle with vertices A,B,C (in some order) is similar to triangle T is
01:26View SolutionThe number of positive integers n in the set `{2,3,....,200}` such that `(1)/(n)` has a terminating decimal expansion is
01:01View SolutionIf a,b,c are real numbers such that a+b+c=0 and `a^(2)+b^(2)+c^(2)=1,` then
`(3a+5b-8c)^(2)+(-8a+3b+5c)^(2)+(5a-8b+3c)^(2)` is equal to03:33View SolutionLet ABC be a triangle and M be a point on side AC closer to vertex C than A. Let N be a point on side AB such that MN is parallel to BC and let P be a point on side BC such that MP is parallel to AB. If the area of the quadrilateral BNMP is equal to `(5)/(18)`th of the area of triangle ABC, then the ratio AM/MC equals.
View SolutionLet `nge4` be a positive integer and let `l_(1),l_(2),.....,l_(n)` be the lengths of the sides of arbitrary n-sided non-degenerate polygon P. Suppose `l_(1)/(l_(2))+l_(2)/(l_(3))+....l_(n-1)/(l_(n))+l_(n)/(l_(1))=n.` Consider the following statements: I. The lengths of the sides of P are equal. II. The angles of P are equal. III. P is a regular polygon if it is cyclic. Then
07:08View SolutionConsider the following statements. For any integer n,
I. `n^(2)+3` is never divisible by 17.
II. `n^(2)+4` is never divisible by 17.
Then01:26View SolutionLet S be the set of all ordered pairs (x,y) of positive intergers, with HCF (x,y)=16 and LCM (x,y) = 48000. The number of elements in S is
01:15View SolutionConsider the set A of natural numbers n whose units digit is nonzero, such that if this units digit is erased, then the resulting number divides n. If K is the number of elements in the set A, then
View SolutionThere are exactly twelve sundays in the period from january 1 to march 31 in a certain year. Then the day corresponding to february 15 in that year is
05:21View SolutionConsider a three-digit number with the following properties:
I. If its digits in units place and tens place are interchanged, the number increases by 36,
II. If its digits in units place and hundreds place are interchanged, the number decreases by 198. Now suppose that the digits in tens place and hundreds place are interchanged. Then the number.07:33View SolutionConsider four triangles having sides (5,12,9), (5,12,11), (5,12,13) and (5,12,15). Among these, the triangle having maximum area has sides
06:12View SolutionIn a classroom, one-fifth of the boys leave the class and the ratio of the remaining boys to girls is 2:3. If further 44 girls leave the class, the ratio of boys to girls is 5:2. How many more boys should leave the class so that the number of boys equals that of girls ?
05:46View SolutionLet X,Y,Z be respectively the areas of regular pentagon, regular hexagon and regular heptagon which are inscribed in a circle of radius 1. Then
04:38View SolutionThe least value of natural number n such that `((n-1),(5))+((n-1),(6))lt((n),(r))," where"((n),(r))=(n!)/((n-r)!r!),is `
01:31View SolutionIn a Mathematics test, the average marks of boys is `x%` and the average marks of girls is `y%` with `xney.` If the average marks of all students is `z%` the ration of the number of girls to the total number of students is
04:24View Solution
Part 1 Mathematics questions and complete solutions for chapter KVPY of KVPY PREVIOUS YEAR of Class 12
