Complete Solutions to MULTIPLE CHOICE QUESTIONS of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| MARVEL | MULTIPLE CHOICE QUESTIONS |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Tidal waves in the sea are primarily due to
View SolutionTwo spheres of masses `M_(1)` and `M_(2)` and separated by a distance d are situated in air and the gravitational force of attraction between them is F. If the two spheres are kept in a liquid of specific gravity 5 then the gravitational force between them will be
View SolutionThe values of the acceleration due to gravity on two planets are `g_(1) - g_(2)`, then the two planets must have the same
View SolutionAt the surface of a certain planet acceleration due to gravity is one - quarter of that on earth If a brass ball is transported to this planet , then which one of the following statements is not correct ? .
View SolutionIf G is the universal constant of gravitation and g is the acceleration due to gravity, then the dimensions of `(G)/(g)` are
View SolutionIf the earth suddenly shrinks (without changing mass) to half of its present radius, then acceleration due to gravity will be
View SolutionThe mean radius of a planet is `6.67xx10^(3)` km. The acceleration due to gravity on its surface is `10 m//s^(2)`. If `G = 6.67xx10^(-11)Nm^(2)//kg^(2)`, then the mass of the planet will be `[R=6.67xx10^(6)m]`
View SolutionA force of 75 Newton acts on a body of mass 2.5 kg at a certain point. The intensity of the gravitational field at that point is
View SolutionA man weighs 'W' on the surface of the earth and his weight at a height 'R' from surface of the earth is (`R` is Radius of the earth )
View SolutionThe acceleration due to gravity on the surface of the moon `= (1)/(6)` the acceleration due to gravity on the surface of the earth. What will be the mass of a steel ball on the surface of the moon, if its mass on the surface of the earth is 6 kg ?
View SolutionIf the mass of the earth remains constant but the diameter of the earth becomes two times its present value, then the weight of a person weighing 80 kg - wt, would be
View SolutionIf the density of the earth is doubled keeping its radius constant then acceleration due to gravity will be `(g=9.8 m//s^(2))`
View SolutionIf `R` is the radius of the earth and `g` the acceleration due to gravity on the earth's surface, the mean density of the earth is
View SolutionThe masses of two planets are in the ratio `1 : 2`. Their radii are in the ratio `1 : 2`. The acceleration due to gravity on the planets are in the ratio
View SolutionA body weighs `700gm` wt on the surface of the earth. How much will it weigh on the surface of a planet whose mass is `1/7` and radius is half that of the earth
View SolutionA satellite of mass 2000 kg is revolving around the earth in a circular orbit of radius `4xx10^(4)` km. The gravitational force exerted by the satellite on the earth is ________. [Mass of the earth `= 6xx10^(24)kg, G=6.67xx10^(-11)Nm^(2)//kg^(2)`]
View SolutionThe time period of a simple pendulum inside a starionary lift is 2 second. What would be its period, when the lift moves upwards with an acceleration `(g)/(4)` ?
View SolutionA mass of 1 kg is supended by a string. It is
(i) lifted up with an acceleration `4.9 m//s^(2)`
(ii) lowered with an acceleration `4.9 m//s^(2)`
Then the ration of the tension in the string in the two cases is
View SolutionA simple pendulum of length L is taken from earth to a planet where the acceleration due to gravity is doubled. What should be its new lenths so that its periodic time is not changed ?
View SolutionThe mass of moon 1% of mass of earth. The ratio of gravitational pull of earth on moon and that of moon on earth will be
View SolutionTwo bodies of equal masses situated at diametically opposite points go around a circle of radius R under the action of their mutual gravitational attraction. The speed (v) of each body is given by
View SolutionThe unit of g/G is
View SolutionThe acceleration due to gravity on the moon is `(1^(th))/(6)` that on the earth. If the earth and the moon are assumed to have the same density, then the radius of the moon is
View SolutionA lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
View SolutionThe radii of two planets are respectively `R_(1) and R_(2)` and their densities are respectively `rho_(1) and rho_(2)`.The ratio of the accelerations due to gravity at their surface is
View SolutionThe acceleration due to gravity on a planet is `1.96 m//s^(2)`. If a boy can safely jump from a height of 2 m on the earth, then the coorresponding safe height on the planet will be
View SolutionTwo speres of radii r and 2r touching each other the force of attraction betweeen them is proportional
View SolutionThe earth (mass `=6xx10^(24)kg`) revolves round the sun with an angular velocity of `2xx10^(-7)"rad/s"` in a circular orbit of radius `1.5xx10^(8)km.` The gravitational force exerted by the sun on the earth, in newtons, is
View SolutionTwo planets have the same average density but their radii are `R_(1)` and `R_(2)`. If acceleration due to gravity on these planets be `g_(1)` and `g_(2)` respectively, then
View SolutionA spherical planet far out in space has a mass `M_(0)` and diameter `D_(0)`. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
View SolutionIf density of earth increased 4 times and its radius become half of what it is, our weight will
View SolutionA man can jump 2 m high on the surface of the earth. How high he can jump on a planet where the acceleration due to gravity is `(g)/(12)`, where g is the acceleration due to gravity on the surface of the earth ?
View SolutionThe densities of two planets are in the ratio of 2 : 3 and their radii are in the ratio of 1 : 2. What is the ratio of acceleration due to gravity at their surfaces ?
View SolutionA binary star system consists of two stars of masses `M_(1)` and `M_(2)` revolving in circular orbits of radii `R_(1)` and `R_(2)` respectively. If their respective time periods are `T_(1)` and `T_(2)`, then
View SolutionAverage density of the earth
View Solutionimagine a new planet having the same density as that of earth but it is 3 times bigger than the earth is size. If the acceleration due to gravity on the surface of earth is g and that on the surface of the new planet is g', then find the relation between g and g'.
View SolutionThe rotation of earth is responsible for the acceleration due to gravity to be
View SolutionIf the radius of the earth were to shrink by one percent its mass remaining the same, the acceleration due to greavity on the earth's surface would
View SolutionA simple pendulum has a time period `T_(1)` when on the earth's surface and `T_(2)` when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `(T_(2))/(T_(1))` is
View SolutionTwo identical spheres each of mass M and radius R are separated by a distance 3R. The force of attraction between them is proportional to
View SolutionA man weighs `80 kg` on the surface of earth of radius `r`. At what height above the surface of earth his weight will be `40 kg`?
View SolutionThe distance between the centres of the Moon and the earth is `D`. The mass of the earth is `81` times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionA research satellite of mass `200 kg` circles the earth in an orbit of average radius `3 R//2`, where `R` is the radius of the earth. Assuming the gravitational pull on the mass of `1 kg` on the earth's surface to be `10 N`, the pull on the satellite will be
View SolutionThe height at which the acceleration due to gravity becomes `g//9` in terms of R the radius of the earth is
View SolutionTwo spheres of masses (m) and (M - m) are prepared from a sphere of mass M. They are kept at a distance x. For what ratio of `(m)/(M)` will the gravitational attraction between them be maximum ?
View SolutionThe mass of a sphereical planet is 5 times the mass of the earth, but its diameter is the same as that of the earth. How much work is done in lifting a stone of mass 3 kg through a distance of 1 m on the planet ? [g on the surface the earth `= 10 m//s^(2)`]
View SolutionThree uniform spheres, A, B and C each of mass M and radius R are kept in such a way that each sphere touches the other two. What is the magnitude of the gravitational force acting on A due to B and C ?
View SolutionF is the gravitational force between two point masses `m_(1)` and `m_(2)` , separated by a distance d. A point mass `2m_(1)` is then brought near `m_(1)`. What is the total force on `m_(2)` ?
View SolutionSuppose that the gravitational force between two bodies separated by a distance R becomes inversely proportional to R (and not as `(1)/(R^(2))` as given by Newton's law of gravitation). Then the speed of a particle moving in a circular orbit of radius R under such a force would be proportional to
View SolutionThe acceleration due to gravity on the planet A is 8 times the acceleration due to gravity on the planet B. A man jumps to a height of 2.5 m on the surface of A. What is the height of jump by the same person on the planet B ?
View SolutionIf the Earth losses its gravity, then for a body
View SolutionThe density of a newly discovered planet is twice that of the earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth be R, then radius of the planet would be
View SolutionTwo bodies A and B of masses 50 kg and 100 kg are kept at a distance of 2 m on the surface of the earth. The gravitational force of attraction between them is F. A and B are then taken to the moon and are kept at the same distance of 2 m. The acceleration due to gravity on the surface of the moon `=(g)/(6)`, where g is the acceleration due to gravity on the earth. What will be the gravitational force of attraction between A and B on the surface of the moon ?
View SolutionAn apple of mass `0.25` kg falls from a tree . What is the acceleration of the apple towards the earth ? Also calculate the acceleration of the earth towards the apple . Mass of the earth = `5.983 xx 10^(24)` kg , Radius of the earth = `6.378 xx 10^(6)` m and G = `6.67 xx 10^(-11)Nm^(2) kg^(-2)`
View SolutionThree particles each of mass m are placed at the three corners of an equilateral triangle of side L. A particle of mass M is kept at the midpoint of any one side. What is the force acting on M, due to this system of 3 particles ?
View SolutionIf the radius of the earth were to shrink by 1% its mass remaining the same, the acceleration due to gravity on the earth's surface would
View SolutionA body weight 45 N on the surface of the earth. What is the gravitational force acting on it due to the earth at a height equal to half the radius of the earth ?
View SolutionA planet has the same size as that of the earth but its mass is 4 times the mass of the earth. What is the energy required to lift a stone of mass 5 kg vertically upwards through 3 m, on the planet ? [g on the surface of the earth `= 10 m//s^(2)`]
View SolutionAssume that the acceleration due to gravity on the surface of the moon is `0.2` times the acceleration due to gravity on the surface of the earth. If `R_e` is the maximum range of a projectile on the earth's surface, what is the maximum range on the surface of the moon for the same velocity of projection
View SolutionTwo objects of masses `m` and `4m` are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If `G` is the universal gravitaitonal constant, then at separation `r`
View SolutionParticles of masses 2M, m and M are respectively at points A, B and C with `AB=(1)/(2)` (BC). M is much smaller than M and at time t = 0, they are all at rest given in the figure. At subsequent times before any collision takes place.
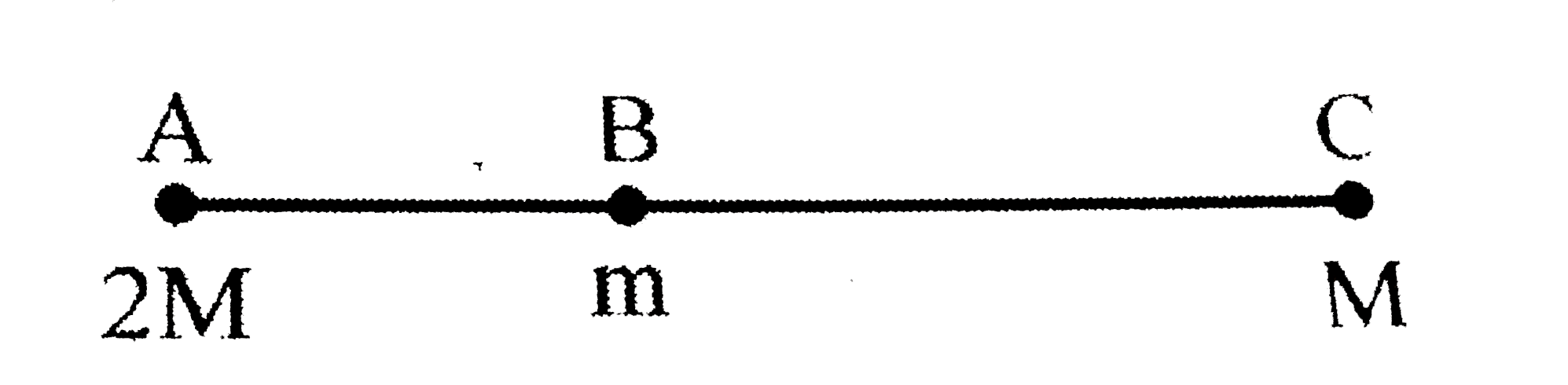
View SolutionHow much faster than it's normal rate should the earth rotate about it's axis so that the weight of the body at the equator becomes zero `(R=6.4xx10^(6)m,g=9.8m//s^(2))` (in times)
View SolutionThe mass and diameter of a planet have twice the value of the corresponding parameters of earth. Acceleration due to gravity on the surface of the planet is
View SolutionThe length of a second's pendulum is 1 m on the earth. If the mass and diameter of a planet than that of earth, then the length of the second's pendulum on the planet will be
View SolutionA satellite is revolving around the earth in a circular orbit at an altitude h where the acceleration due to gravity is g'. If the earth is a sphere of radius R then the period of the satellite is give by
View SolutionThe orbital velocity for an earth satellite near the surface of the earth is 8 km/sec. If the radius of the orbit is 4 times the radius of the earth, its orbital velocity will be
View SolutionIf the radius of earth's orbit is made 1/4, the duration of an year will become
View SolutionTwo satellites X and Y are moving in circular orbits of radii R and 2R respectively, around the same planet. What is the ratio of their critical velocities ?
View SolutionTwo satellites orbiting around the earth have their critical speeds in the ratio 4 : 5. What is the ratio of their orbital radii ?
View SolutionThe critical speed of a satellite orbiting very close to the surface of the earth is `[g=10 m//s^(2)` and `R=6.4xx10^(-6)m]`
View SolutionTwo satellites are moving at heights of R and 5R above the surface of the earth of radius R. The ratio of their velocitirs `((V_(1))/(V_(2)))` is
View SolutionTwo satellites of masses 80 kg and 120 kg revolve round a planet in circular orbits of radii 16 R and 9 R respectively, where R is radius of the planet. The ratio of the speeds of satellites will be
View SolutionThe critical speed of a satellite of mass 500 kg is 20 m/s. What is the critical speed of a satellite of mass 1000 kg moving in the same orbit ?
View SolutionA body weighs W newton at the surface of the earth. Its weight at a height equal to half the radius of the earth, will be
View SolutionA satellite of mass `m` is circulating around the earth with constant angular velocity. If the radius is `R_(0)` and mass of earth is M, then the angular momentum about the centre of the earth is
View SolutionThe period of a satellite moving very close to the surface of the earth of radius R is 84 minute. What will be the period of the same satellite, if is is taken at a distance of 3R from the surface of the earth ?
View SolutionWhen a satellite revolves around the sun in a circular orbit of radius a with a period of revolution T, and if K is a positive constant, then
View SolutionIf T is the period of a satellite revolving very close to the surface of the earth and if `rho` is the density of the earth, then
View SolutionA satellite is orbiting around the earth. If both gravitational force and centripetal force on the satellite is `F`, then, net force acting on the satellite to revolve around the earth is
View SolutionTwo planets at mean distance `d_(1)` and `d_(2)` from the sun and their frequencies are n and n respectively then
View SolutionTwo satellites of masses M and 4M are orbiting the earth in a circular orbit of radius r. Their frequencies of revolution are in the ratio of
View SolutionThe distances of two planets A nad B from the sun are `10^(12)m` and `10^(11)m` and their periodic times are `T_(A)` and `T_(B)` respectively. If their orbits are assumed to be circular, then the ratio of their periodic times `((T_(A))/(T_(B)))` will be
View SolutionThe time of revolution of planet `A` round the sun is `8` times that of another planet `B`. The distance of planet `A` from the sun is how many `B` from the sun
View SolutionA satellite going around the earth suddenly loses height and starts moving in an orbit of smaller radius. Then its periodic time
View SolutionAn artificial satellite is moving in a circular orbit around the earth, with a speed which is equal to half the magnitude of the escape velocity from the earth. What is the height of the satellite above the surface of the earth ?
View SolutionTwo satellites A and B go around a planet in circular orbits of radii 4 R and R respectively. If the speed of the satellite A is 3 V, then the speed of the satellite B will be
View SolutionA satellite going around the earth suddenly loses height and starts moving in a lower orbit. The speed of the satellite
View SolutionOrbital radius of a satellite S of earth is four times that s communication satellite C. Period of revolution of S is :-
View SolutionThe earth revolves around the sun in an elliptical orbit. It has a speed `v_(1)` when it is at the minimum distance `d_(1)` from the sun. When it is at the maximum distance `d_(2)` from the sun, its speed is
View SolutionA satellite of the earth is revolving in a circular orbit with a uniform speed `v`. If the gravitational force suddenly disappears, the satellite will
View SolutionIf the orbital velocity of a planet is given by `v = G^(a) M^(b) R^(c )` then
View SolutionThe earth E moves in an elliptical orbit around the sun, with the sun S at one of the foci as shown in the figure. Its maximum and minimum speeds of motion will be at points

View SolutionA saturn year is 29.5 times the earth year. How far is the saturn from the sun if the earth is `1.5xx10^(8)` away from the sun?
View SolutionWhat is the periodic times of a satellite revolving very close to the surface of the earth, of density `rho` ?
View SolutionA satellite A of mass m is at a distance of r from the centre of the earth. Another satellite B of mass 2m is at distance of 2r from the earth's centre. Their time periode are in the ratio of
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. What is the time period of another satellite orbiting at a height of 2.5 R from the surface of the earth ?
View SolutionThe time period of an earth satellite in circular orbit is independent of
View SolutionTwo satellites of earth `S_(1)` and `S_(2)` are moving in the same orbit. The mass of `S_(1)` is four times the mass of `S_(2)`. Which one of the following statements is true?
View SolutionIf the sun and the planets carried huge amounts of opposite charges
View SolutionA satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
View Solution
MULTIPLE CHOICE QUESTIONS questions and complete solutions for chapter GRAVITATION of MARVEL PHYSICS (HINGLISH) of Class 12